基于擺度規(guī)律與CAD相結合的導瓦間隙分配算法研究及應用
劉鋼鋼,孟 騰,臧衛(wèi)杰,陶 健
(1.黃河水利水電開發(fā)總公司,河南省濟源市 459017;2.水利部小浪底水利樞紐管理中心,河南省鄭州市 450000)
0 引言
立式水輪發(fā)電機組軸承瓦間隙分配計算調整是機組安裝及檢修過程中的一項重要工作,瓦間隙調整的精準度直接影響著機組運行中的振動、擺度、瓦溫等重要性能指標。瓦間隙計算調整在機組軸線調整合格后進行,應統(tǒng)籌考慮導軸瓦位置、設計間隙、盤車擺度及主軸停留位置等因素,基本要求是通過合適的瓦間隙分配,讓同一部位導軸承的各塊軸瓦分布在同一分布圓上,且確保各部位導軸承同心并且其中心連線與已經確定的理論旋轉中心重合,按照盤車擺度大的位置其對應的瓦間隙小的原則進行,因此,瓦間隙計算分配是一項技術要求高且較為復雜的工作。
姜政權等[1-2]采用傳統(tǒng)等角八點法瓦間隙算法,其缺少公式推導過程,工程人員難于理解,公式計算繁瑣,計算采用的盤車擺度點不一定是實際最大擺度點,且根據其計算結果,機組同一部位導軸承的各瓦面不一定分布在同一圓周上;鄧震宙等[3-4]運用CurveExpert、Excel繪圖工具計算盤車數據,根據曲線確定最大擺度點存在較大誤差;楊云等[5-8]運用最小二乘曲線擬合法、孟安波[9]采用遺傳算法、彭鋮[10]采用粒子群算法對盤車數據進行了仿真研究,提高了盤車計算的準確度,但限于現場工程技術人員理論知識儲備有限,其現場操作應用難度較大;林煥森等[11-14]根據軸線偏移原理推導了八點盤車的擺度特性,運用幾何分析確定了最大擺度點的數據,但存在計算速度較慢且易出錯等問題。
本文在前人研究成果的基礎上,提出一種基于擺度規(guī)律與AutoCAD快速標注相結合的瓦間隙計算方法,該算法已成功應用在小浪底水電站瓦間隙計算過程中,應用效果良好,為其他同類型水電站瓦間隙計算分配提供了借鑒。
1 盤車數據計算分析
1.1 擺度特性分析
立式水輪發(fā)電機組在制造、安裝或檢修回裝過程中,由于存在誤差情況,鏡板水平面與機組軸線不會達到理論垂直水平,且存在主軸各法蘭結合面與機組軸線不垂直的情況,導致機組軸線與其理論旋轉中心線不重合,形成沿旋轉軸軸向方向呈圓錐形的軸線運動,如圖1所示。
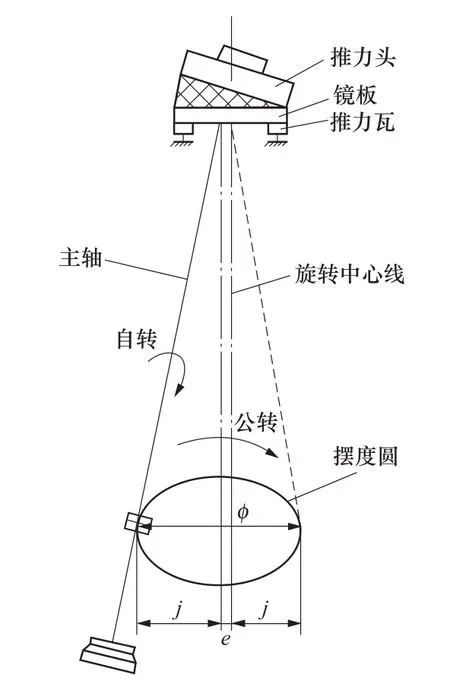
圖1 主軸旋轉示意圖Figure 1 Schematic diagram of spindle rotation
立式水輪發(fā)電機組旋轉過程中,可建立簡化其旋轉擺度模型,如圖2所示。

圖2 擺度模型示意圖Figure 2 Schematic diagram of pendulum model
在等角12點盤車系統(tǒng)中,假設機組的理論旋轉中心為O,某一測量主軸截面圓瞬時圓心為O1,圓周A點位置軸號1是位于軸上的點,此時軸號1的百分表的讀數δ1;當主軸旋轉180°,主軸截面圓瞬時圓心為O2,軸號1將到達-Y軸上的A′點,軸號7′將到達+Y軸上的B點,此時百分表讀數為δ7′,則δ1與δ7′之差亦即線段AB的長度即為該測量部位方位1~7′的全擺度。
在圖2上,分別過點O1和點O2向Y坐標軸作垂線,垂足分別為C和D;假設OO1=OO2=e,O1A=O2B=R,∠AOO1=θ。其中,e為主軸截面圓心相對于旋轉中心的偏心距;R為主軸截面圓半徑;θ為軸號與主軸截面圓圓心相對于旋轉中心的方位夾角。
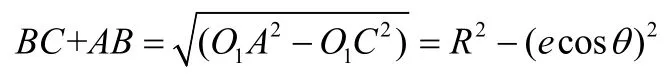
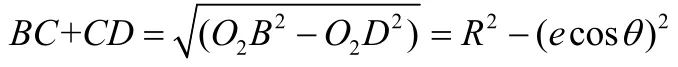
所以:AB=CD=2ecosθ

1.2 最大盤車擺度點確定
在機組實際盤車數據處理過程中,凈全擺度概念為擺度特性規(guī)律的近似應用。在圖2中,擺度公式中的擺度為軸面上位于旋轉中心兩側成180°的軸號1及軸號7′經過同一百分比時的讀數差;而盤車數據處理中的凈全擺度為軸面上位于主軸截面圓直徑方向的軸號1及軸號7經過同一百分表時的讀數差。由幾何知識可知,當且僅當軸號1位于旋轉中心和主軸截面圓圓心連線的延長線上時,上述擺度測量模型中的軸號7與軸號7′才會完全重合,此時該方位的凈全擺度才與擺度完全一致,因此,從工程計算角度考慮,需作如下假設:①機組軸徑R遠大于偏心距e;②為減小計算誤差,用擺度公式中的值代替凈全擺度進行盤車計算;③忽略百分表及主軸圓度偏差。即便在軸號7與軸號7′在不重合的情況下,二者位置上也將極為接近。
綜上所述,將凈全擺度等同于擺度公式中的擺度的處理方式是可行的,既方便計算,又保證了精度。在等角12點盤車系統(tǒng)中,由于各軸承部位百分表讀數只有12個數據,計算后僅有6個凈全擺度數據,其數據表格中的凈全擺度最大值作為實際最大擺度值進行計算往往是存在誤差的,實際上,主軸各軸號測點往往不在實際最大擺度方位上,需依據擺度公式對盤車數據進一步進行處理,求取實際最大凈全擺度,作為瓦間隙計算的基礎。
假設盤車計算數據表格中最大凈全擺度值φ1,次最大凈全擺度值為φ2,根據正弦或余弦曲線特點,在等角12點法的盤車系統(tǒng)中,二者相位角角度差為30°,而且實際最大凈全擺度方位將位于盤車數據的最大凈全擺度方位和次最大凈全擺度方位之間。假設實際最大凈全擺度值為φmax,則φmax=2e;假設實際最大凈全擺度φmax與盤車數據表格中最大凈全擺度φ1相角差為ε,則實際最大凈全擺度φmax與盤車數據表格中次最大凈全擺度相角差為30°-ε。根據擺度計算公式:

由式(1)、式(2)可以得出:
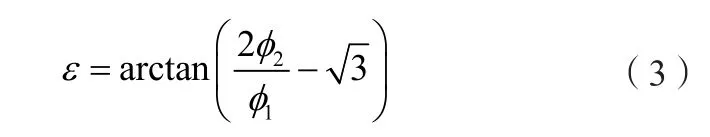
進而可以利用ε求出實際最大擺度:

綜上,實際最大擺度及其方位是可以利用式(1)、式(2)由盤車數據表格中的最大凈全擺度和次最大凈全擺度精確計算出來。
1.3 CAD快速計算分析
通常,機組導軸瓦間隙計算簡化公式[15]如式(5)所示:

式中:δ表示計算出來的應調整瓦間隙,C0表示單邊設計瓦間隙,φ表示實際最大凈全擺度值,α表示需調整導瓦中心與實際最大凈全擺度相位角差。
式(5)的幾何意義可利用圖3進行解釋。在圖3中,假定半徑OE值為C0,線段OF長度值為φ/2,OF與OE夾角為α,由F點向OE作垂線,垂足為G點,則EG長度值即為δ。推而廣之,在AutoCAD制圖環(huán)境下,用CAD標注功能可直接顯示EG長度值。避免了傳統(tǒng)的通過計算實際最大凈全擺度與各軸瓦相位角,再依次代入公式(5)中反復計算各軸瓦間隙值,不但提高了計算的準確度,而且極大地提高了計算的速度。
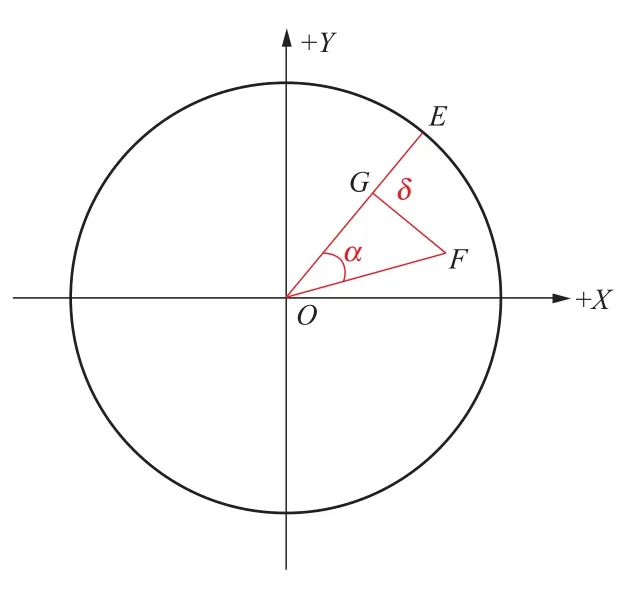
圖3 幾何分析示意圖Figure 3 Geometric analysis diagram
下面以計算某軸承1號軸瓦分配間隙為例進行分析。如圖4所示表示該軸承瓦及盤車點號分布示意圖。假設該軸承有10塊分塊瓦,盤車數據中最大凈全擺度在10點軸位上,根據式(4)計算出其實際最大凈全擺度值為φ/2,以OF表示φ/2,OE表示單邊設計瓦間隙。由F點向1號瓦面中心線做垂線,垂足為G,用CAD標注工具中的對齊標注,對線段EG進行標注,其標注值即為1號瓦間隙值。
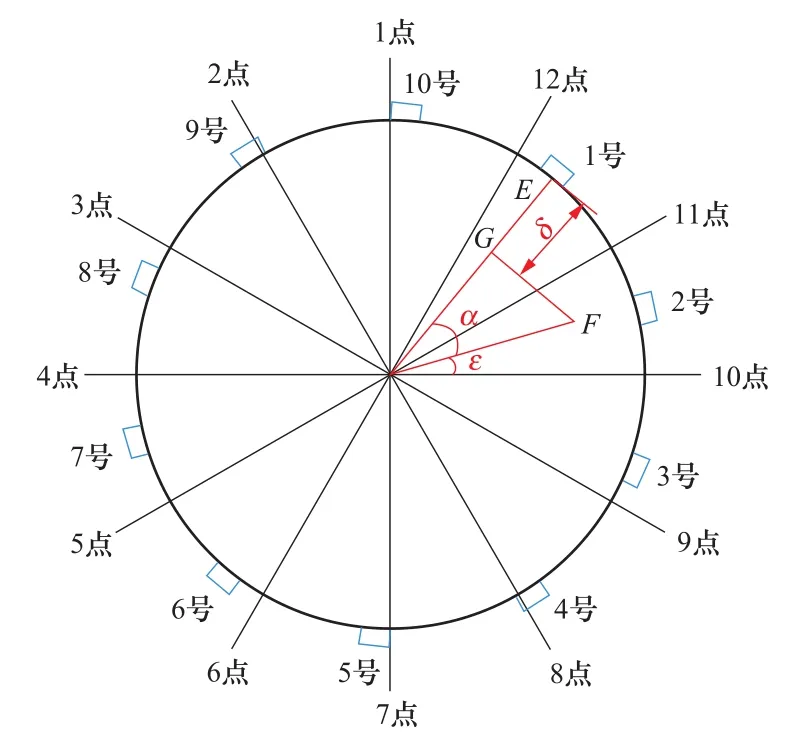
圖4 某軸承瓦及盤車點號分布示意圖Figure 4 Distribution diagram of bearing tile and turning point
2 計算實例
小浪底水電站安裝6臺300MW混流式水輪發(fā)電機組,機組有上導、下導、水導三部導軸承,各部導軸瓦均為分塊式同心瓦,其中,上導瓦12塊、下導瓦12塊、水導瓦10塊,設計單邊間隙值分別是上導為0.18mm、下導為0.20mm、水導為0.25mm。在3號水輪發(fā)電機組大修盤車過程中,采取抱上導的12點盤車法,機組軸線調整合格后,其盤車數據及數據處理結果見表1。
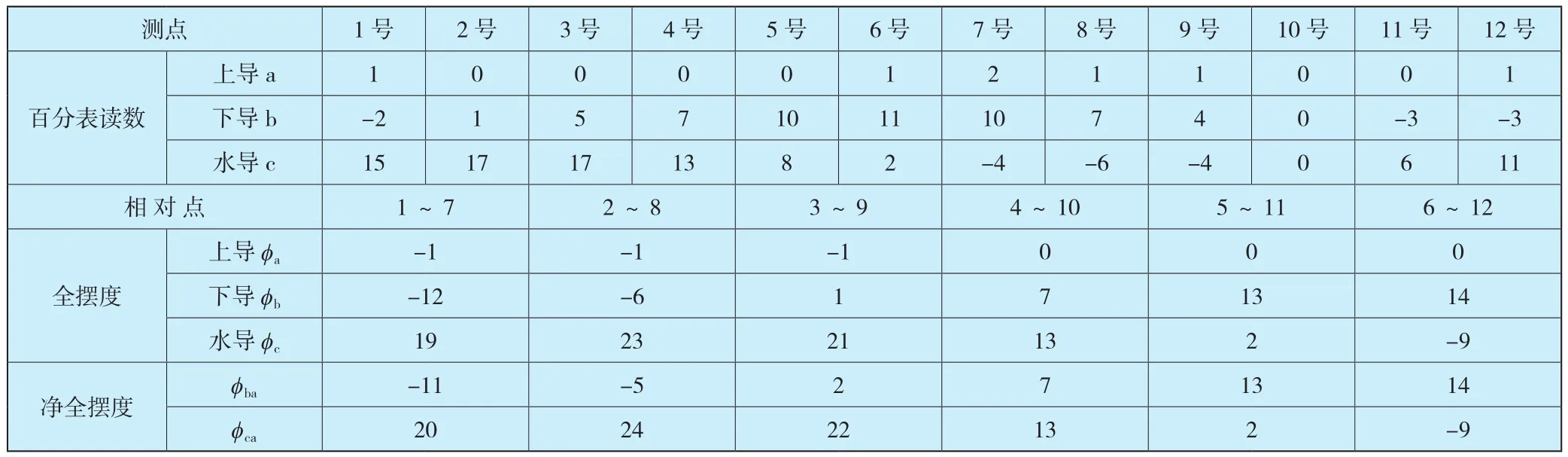
表1 盤車數據及數據處理表Table 1 Turning data and data processing table 0.01mm
從表1可以看出,下導盤車最大凈全擺度φb1=0.14mm(位于6號軸位),盤車次最大凈全擺度φb2=0.13mm(位于5號軸位);水導盤車最大凈全擺度φc1=0.24mm(位于2號軸位),盤車次最大凈全擺度φc2=0.22mm(位于3號軸位)。將下導、水導盤車最大凈全擺度、次最大凈全擺度分別代入式(3)、式(4),可分別計算出下導實際最大凈全擺度φbmax=0.141mm,相位角差ε1=7.1°;水導實際最大凈全擺度φcmax=0.241mm,相位角差ε1=5.8°。
下面依據精確計算出的實際最大凈全擺度及與盤車最大凈全擺度相位角差計算各部軸承瓦間隙值。
上導瓦:由于小浪底電站3號機組盤車過程中采取抱上導瓦方式,其他部位軸承都是以上導為基礎調整,所以上導軸頸的轉動中心近似可以看成是理想中心,故上導采用均抱瓦的方式,即上導軸瓦的實際間隙值等于設計間隙0.18mm。
下導瓦:在CAD制圖環(huán)境下,以下導瓦單邊設計間隙值0.2mm為半徑畫坐標圓,然后作出實際最大凈全擺度以及各導瓦分布示意圖,分別向各導瓦中心線作垂線,隨后對垂足到各導瓦中心的線段進行標注,其標注值即為應調整瓦間隙值。具體情況如圖5所示。

圖5 下導瓦間隙計算示意圖Figure 5 Schematic diagram of clearance calculation of lower guide tile
由圖5可知:δb6=0.1867mm,δb7=0.1538mm,δb8=0.1334mm,δb9=0.1308mm,δb10=0.1467mm,δb11=0.1769mm。
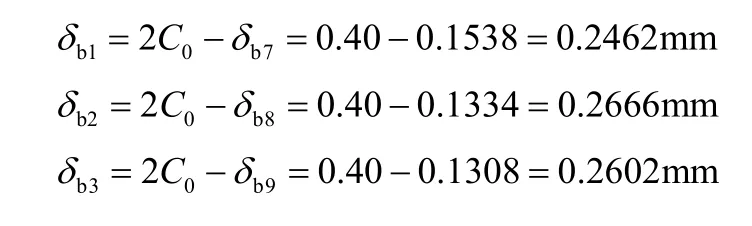
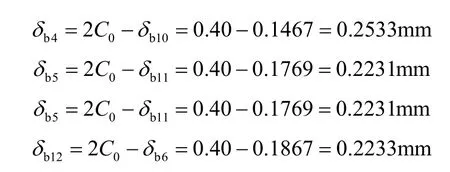
水導瓦:作圖方法參照下導瓦間隙計算方法,具體如圖6所示。
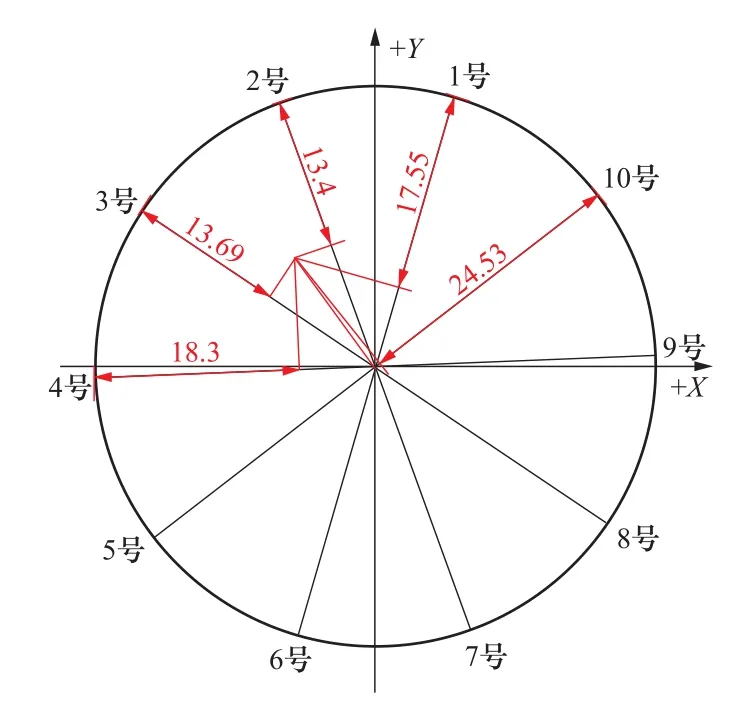
圖6 水導瓦間隙計算示意圖Figure 6 Schematic diagram of calculation of water guide tile clearance
由圖6可知:δc1=0.1755mm,δc2=0.134mm,δc3=0.1369mm,δc4=0.183mm,δc10=0.2453mm。

綜上,小浪底水電站3號機組上導、下導、水導瓦間隙計算的最終結果見表2。

表2 軸承瓦間隙值Table 2 Bearing tile clearance value 0.01mm
3 結束語
本文提出的基于擺度規(guī)律與CAD相結合的瓦間隙分配算法,通過計算出實際最大凈全擺度,結合AutoCAD快速標注實現瓦間隙快速精準計算。將該方法應用于工程實際中對小浪底水電站3號機組瓦間隙分配進行計算,得到如下結論:
(1)通過分析擺度模型特性,推導出實際最大凈全擺度計算算法,較直接采用盤車最大擺度點的傳統(tǒng)盤車算法精度更高。
(2)結合AutoCAD快速標注法,較傳統(tǒng)手工計算更加高效。
(3)該瓦間隙分配算法對工程技術人員來說簡單易懂易操作,無經濟成本,可供同行參考。

