光電管耦合FitzHugh-Nagumo 神經元的同步*

張秀芳 馬軍 徐瑩 任國棟?

1) (蘭州理工大學物理系, 蘭州 730050)

2) (山東師范大學數學與統計學院, 濟南 250014)

感光細胞能接收各種強度的可見光, 并轉換為生物電信號連接視神經; 這樣的功能可以用光電效應來模擬.本文利用數值計算, 分析了基于光電管耦合FitzHugh-Nagumo (FHN)神經元的動力學特性, 詳細討論了光電管的參數空間中, 混沌和簇放電模式下耦合系統的同步區間.結果表明: 在耦合強度較小時, 耦合系統由于受迫共振表現為完全同步; 耦合強度較大時, 耦合系統傾向于相位同步.光電管的導通狀態, 即反向截止電壓對系統同步具有調制作用.這項工作有助于理解視網膜疾病, 如黃斑變性的原理.

1 引 言

在生物組織和系統中的每個功能單元區域都包含著成千上萬的神經元, 神經元作為神經系統的基本功能單位[1], 能感受刺激并傳導興奮, 具有聯絡和整合輸入信息并傳出信息的作用.神經系統信號編碼和傳輸出現故障可能導致很多的神經疾病,比如帕金森氏癥、阿爾茲海默癥和癲癇等[2].從實驗角度直接在生物系統中開展研究是比較復雜的,而神經元電路[3?6]的設計和控制為研究神經元之間的信息編碼和信息傳遞提供了有效的途徑.對比單個神經元電路模型[4,7?10]與普通的非線性電路[11?13]的輸出序列, 調控神經元電路可以產生靜息態、尖峰放電態、周期態、混沌態和簇放電態等多種復雜的放電模式.

用于搭建神經元電路的電子器件主要有電阻、電容、電感、約瑟夫森結等[14?18], 這些電子元件也可以用來連接兩個或者多個神經元電路.實際的生物神經元在收到外界各類刺激后會產生對應的等效電流來改變神經元的輸出模態, 即神經元的編碼過程伴隨著信號的傳遞.例如, 聽覺神經元可以將振動信號轉化為電刺激信號; 感熱神經元可以將溫度熱信號轉化為電刺激信號; 視覺神經系統中的神經元對光信號敏感, 比如視網膜外感光是一種廣泛的生物學現象, 與光的相關行為和激素的反應有關, 而一些無脊椎動物也擁有簡單的感光器, 比如小龍蝦的尾神經節中的感光器等[19?22].因此通過神經電路的搭建構造具有感知功能的神經電路是有意義的.電子器件例如憶阻器、熱敏電阻和光電管等可以用來搭建功能性神經電路.例如, Liu等[23]和Li 等[24]利用光電管與神經電路嵌合產生了連續的電壓源, 用以捕獲外部光信號.此外, 由于神經系統內的神經元并非孤立存在, 而是與其他神經元連接并完成特定的功能[25?28], 因此上述電子器件也可以用來耦合神經元電路, 使耦合的神經電路系統具有感知外界信號的功能性神經系統.

從生物學角度來看, 生物需要通過進食或者其他方式補給由于生物活動而產生的能量的消耗來維持代謝過程.而從物理學和動力學角度來看, 光電管可以吸收外界光能量轉化為電信號[29]來驅動電路, 給系統注入能量并對系統能量輸運進行調節, 因此通過光電管耦合神經元電路討論耦合系統的放電活動具有重要的意義[30?34].一般耦合兩個或者多個非線性電路可分為兩種, 即單向耦合[35?39]和雙向耦合[40?45].通常電突觸是雙向的.本文通過光電管耦合兩個FitzHugh-Nagumo (FHN)神經元, 在接受外界光照輻射后, 光電管向耦合系統注入能量, 從而改變耦合系統的動力學行為.

2 模 型

FHN 神經元模型是由FitzHugh[46]和Nagumo等[47]提出的可激發神經元的動力學模型, 通過設置適當的參數和外部激勵來描述神經元放電活動.圖1 是由外部電壓源驅動的神經元等效電路圖, 其中NR是非線性電阻,C表示電容,L為感應線圈,R是與感應線圈串聯的電阻,iS代表外部刺激電流,E為施加的恒定電壓源,VS為電壓源,RS為支路的電阻.

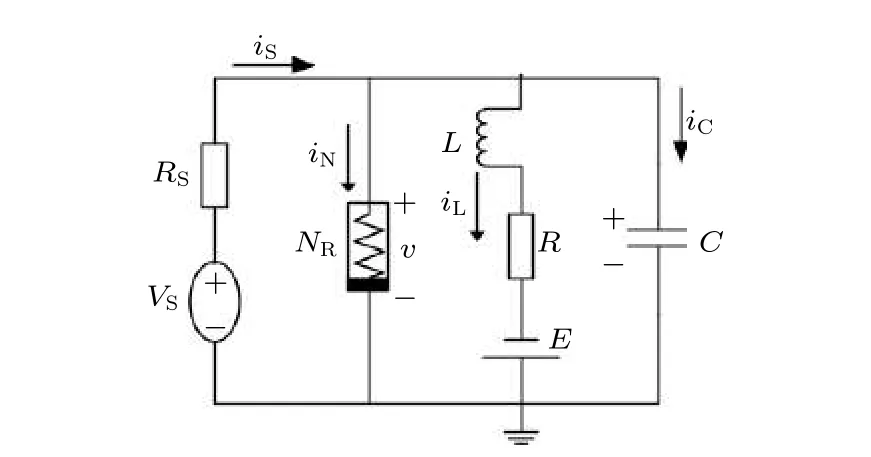
圖1 FHN 神經元的等效電路圖Fig.1.Equivalent circuit diagram of FHN neuron.

根據基爾霍夫定律及電路中各元件電壓電流關系, 圖1 所示的電路方程組為

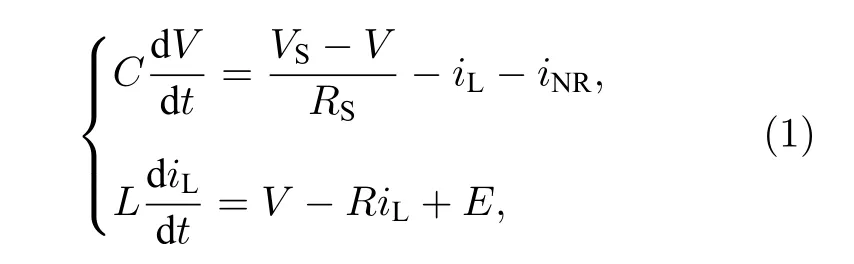
式中,V是電容C兩端的電壓;iL是流經感應線圈的電流; FHN 電路中非線性電阻的伏安特性為

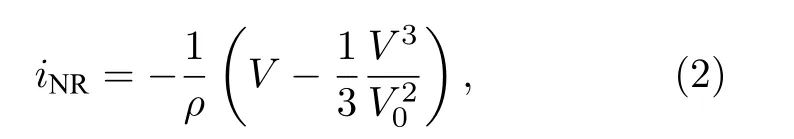
其中,ρ和V0為歸一化參數; 外部激勵VS=BS+B0cos(2πf0t).為了便于數值計算和動力學分析, 將電路方程(1)的參數和變量無量綱化:

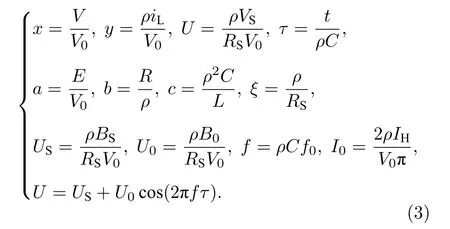
經過標度變換后, 神經元電路等效表達為無量綱的神經元振子模型:

其中,x表示跨膜電壓;y表示不應期;U表示膜電流即神經元的外部激勵;a,b,c分別表示膜半徑、膜內流體的特征阻抗和溫度系數[48?51].

理想光電管的電壓電流特性如圖2 所示.圖2中曲線在橫坐標V軸上的截距Va表示光電管陰極的反向截止電壓, 與材料的功函數(正比于紅限頻率)相關, 當入射光頻率大于紅限頻率時, 光電管產生光電流[52].根據文獻[23], 光電管的電流-電壓關系可以描述為

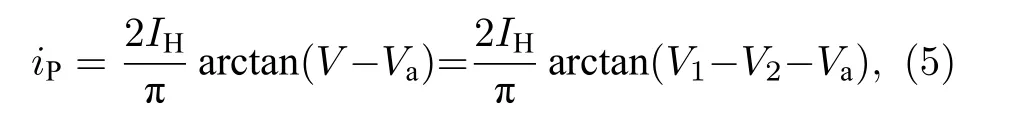
其中參數iP對應流經光電管的電流;IH對應光電管的飽和電流;V=V1–V2對應光電管的陰極和陽極側電壓差, 當光電管的陰極和陽極側電壓差增大時, 陽極對光電子的收集能力增強, 光電流增大,耦合系統之間的信息交互能力增強;Va對應光電管的反向截止電壓, 光電管的反向截止電壓越高,則一定光強下的光電流越小.如果用光電管耦合兩個系統, 那么光電管的反向截止電壓越高時, 耦合系統之間實現信息交互的電流越小, 等效的耦合調制能力較弱.(5)式通過引入表征反向截止電壓的Va項, 在一定程度上表征了單光子光電效應的這種頻率選擇效應.

圖2 光電管的電流-電壓特性Fig.2.I-V characteristics of phototube.

真空光電管正常工作時不僅存在光電流, 還存在三種額外的電流, 即暗電流、本底電流和反向電流.暗電流來源于熱電子發射和噪聲, 為了簡單起見, 認為暗電流和工作電流相比可以忽略; 本底電流是漫反射的雜散光造成的, 通過濾波透鏡可以消除它的影響; 反向電流來自陽極的光電效應, 實踐中陽極材料即使逸出功較陰極大, 也會在使用過程中受到陰極污染而表現出顯著的反向電流; 這也是實驗過程中測到反向電壓超過反向截止電壓仍能測到漏電流的主要原因.(5)式給出的模型能夠在一定程度上反映光電管的反向漏電.

通過光電管耦合的兩個FHN 神經元電路, 等效電路圖如圖3 所示.當兩個具有外界激勵的FHN 電路激活時, 光電管充當電壓源或者電流源為電路提供能量.為簡單起見, 先討論兩個參數相同的FHN 神經元電路, 即令C1=C2,L1=L2,E1=E2,R1=R2,RS1=RS2; 根據基爾霍夫定律,圖3 所示耦合神經元電路的無量綱化方程可表示為

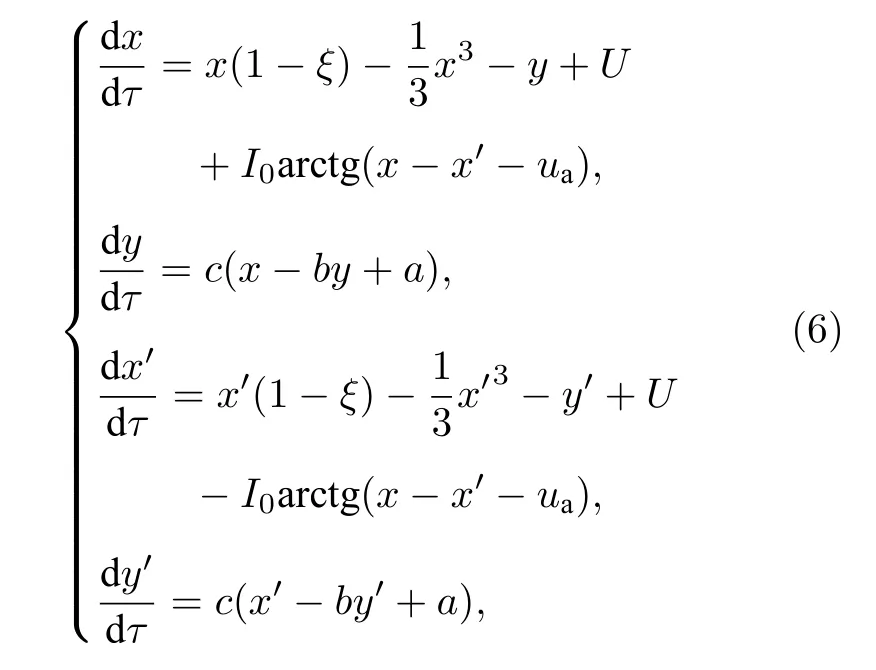
其中耦合強度I0與光電管飽和電流有關,ua與光電管的反向截止電壓有關.光電管可以通過吸收外界光能量調節系統之間的能量輸運, 定義光電管的瞬態功率:

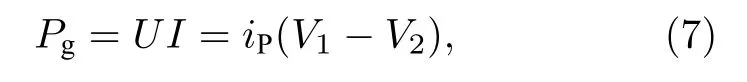
相應的無量綱化功率為

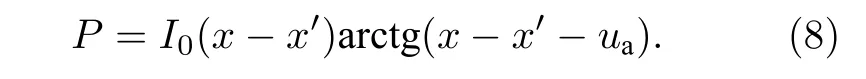
為了判斷耦合系統間的完全同步, 定義系統間誤差函數為

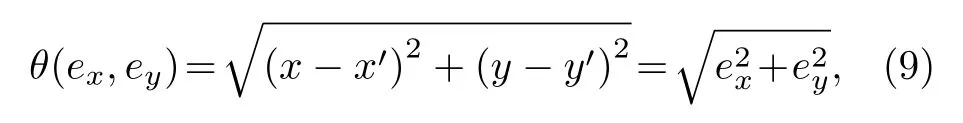
如果誤差函數值隨著時間演化衰減到零, 則表示系統實現完全同步.為了計算兩個系統之間的相位關系, 對時間序列x(t),x'(t)采用Hilbert 變換得到相位序列:

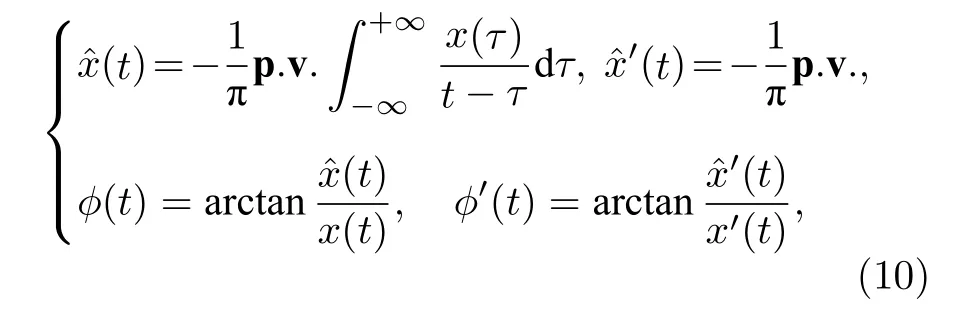
其中p.v.代表柯西積分.相應時間序列x與x'的相位鎖定關系為

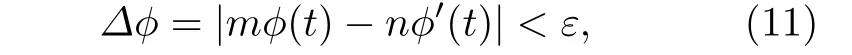
其中,m,n是整數,ε是一個極小值, 如ε≈0.00001, 表示系統達到了n∶m的鎖相.本文計算m∶n= 1∶1 的情況.

3 數值結果與分析

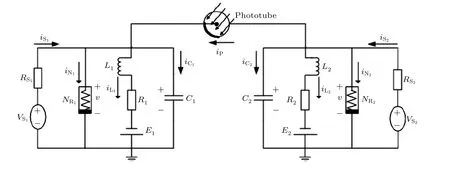
圖3 光電管耦合FHN 神經元系統的等效電路圖Fig.3.Equivalent circuit diagram of the coupled FHN neuron system.

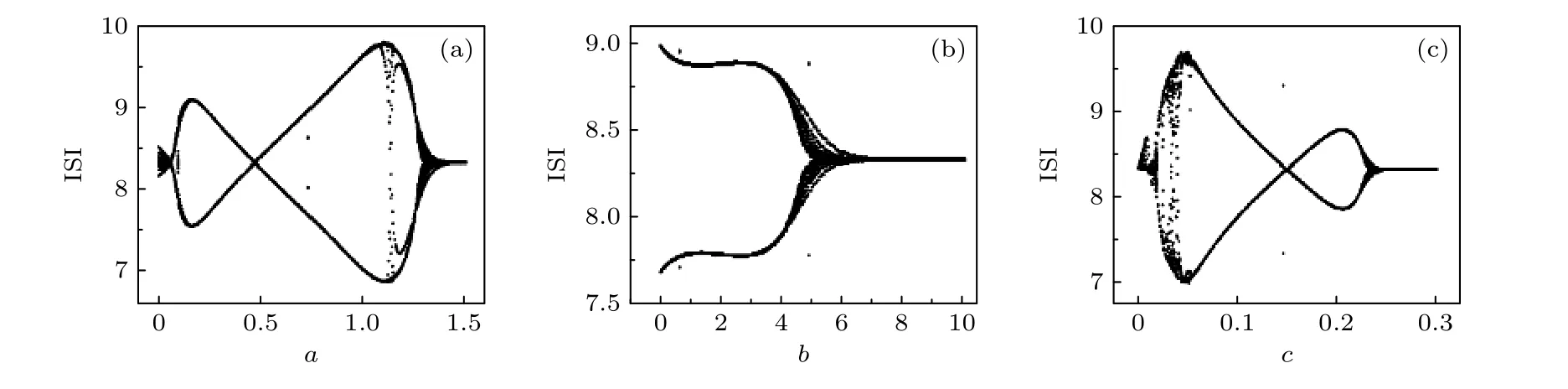
圖4 單個FHN 神經元在不同參數下的ISI (a) b = 0.8, c = 0.1; (b) a = 0.7, c = 0.1; (c) a = 0.7, b = 0.8Fig.4.ISI of single FHN neuron with different parameters: (a) b = 0.8, c = 0.1; (b) a = 0.7, c = 0.1; (c) a = 0.7, b = 0.8.

表1 不同外界刺激頻率下的耦合FHN 神經元分類Table 1.Category of the coupled FHN neurons driven by external stimulation with different frequencies.

本節主要討論基于光電管耦合兩個FHN 神經元的動力學特性, 在數值模擬中, 采用四階Runge-Kutta 算法, 積分步長h= 0.01, 計算的時間為1000 個時間單位.首先根據(4)式計算了具有外界刺激U=Us+U0cos(2πfτ)的單個FHN 神經元模型在不同參數下的峰峰間隔(interspike interval,ISI), 系統參數選擇為ξ= 0.175,Us= 0,U0=0.9,f= 0.16, 初始值為(0.2, 0.1), 計算結果如圖4所示.

從圖4 的結果發現, 不同的參數取值使得系統出現不同的放電模式; 當參數a, c變化時, 神經元從兩周期放電模式向單周期放電轉變時存在交替特征, 如圖4(a)和圖4(c)所示; 當參數b變化時,神經元從兩周期放電轉變為單周期放電表現出較一致的特征, 如圖4(b)所示; 此外, 外界激勵的幅度或頻率也能夠影響神經元的興奮性, 使得神經元處于不同的放電狀態.因此分類討論了不同刺激頻率下耦合兩個處于不同放電狀態下FHN 神經元的情況, 如表1 所列.文中參數設置均為a= 0.7,b= 0.8,c= 0.1,ξ= 0.175,Us= 0,U0= 0.9, 耦合系統初始值為(0.2, 0.1; 0.2, 0.3).

3.1 混沌放電FHN 神經元的光電管耦合(f = 0.16)

對于(6)式所示的耦合系統, 為探究耦合項中I0和ua的影響, 繪制出激勵源頻率f= 0.16 情況(case 1, 2)下, 耦合系統隨I0和ua變化的峰峰間隔圖(ISI), 如圖5 所示.

從圖5(a)和圖5(d)可以看出,I0和ua會使系統的放電模式發生變化; 在外界激勵U相同的情況下, 增大I0會使系統的混沌放電轉換為周期放電, 如圖5(b)和圖5(c)所示.同樣ua對系統的放電模式同樣具有重要的作用, 在ua增大時系統處于混沌放電狀態(圖5(d)的ISI 圖所示), 對應的放電波形如圖5(e)和圖5(f)所示, 其中小圖為對應參數下功率譜的計算, 圖5(e)功率譜圖為離散的, 可知系統是多周期的; 而圖5(f)的功率譜為連續的, 可知系統處于混沌態.對于第一種情況(case 1), 計算了參數空間中的最大誤差函數θmax與最大相位差Δφmax, 如圖6 所示.

如圖6(a)所示,I0趨于0 時系統中存在完全同步流形, 但是隨著I0增大, 系統表現為去(完全)同步; 不同于完全同步, 如圖6(b)所示, 隨著I0增大, 相位差減小有實現同步的傾向, 并在I0=0.79 時出現相位差趨于0; 但是增大ua使得相位同步出現“舌頭”, 如圖6(b)右側所示.耦合系統的誤差函數、相位差以及對應參數下的光電管功率的時間序列計算結果如圖7 所示.

從圖7(a)—(d)可以看出,I0的增大使得誤差函數趨于增大, 系統遠離完全同步; 但是如圖7(e)—(h),I0的增大可以促進耦合系統間的相位同步.此外, 如圖7(i)—(l)所示, 隨著I0的增大,光電管的功率不斷增加, 表明光電管通過吸收光能向耦合系統注入的能量越多, 從而使耦合系統趨于相位同步; 但是通過計算光電管單位光強的功率可以發現, 在系統趨于相位同步后, 光電管單位光強的功率峰值有趨于飽和的特征.對于第二種情況(case 2), 具有較大ua(ua= 0.5)時耦合系統間的誤差及對應的相位差計算結果如圖8 所示.

圖5 耦合系統中神經元的ISI 和放電序列(f = 0.16) (a) ua = 0.1; (b) I0 = 1.5, ua = 0.1; (c) I0 = 2.5, ua = 0.1; (d) I0 = 0.3;(e) ua = 1.5, I0 = 0.3; (f) ua = 2.3, I0 = 0.3Fig.5.ISI and the firing sequence of neuron in the coupled system (f = 0.16): (a) ua = 0.1; (b) I0 = 1.5, ua = 0.1; (c) I0 = 2.5, ua =0.1; (d) I0 = 0.3; (e) ua = 1.5, I0 = 0.3; (f) ua = 2.5, I0 = 0.3.

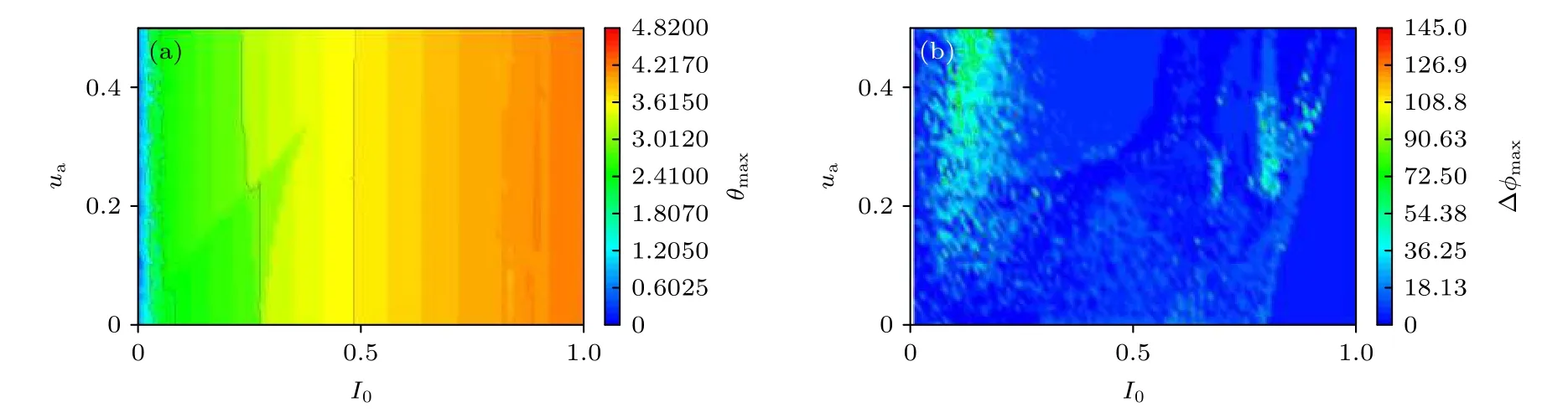
圖6 ua 和I0 的參數空間中, 耦合系統(case 1)的同步區間 (a)最大誤差函數θmax; (b)最大相位差ΔφmaxFig.6.Synchronization region of the coupled system (case 1) in the parameter space of ua vs.I0: (a) Maximum error function θmax;(b) maximum phase difference Δφmax.

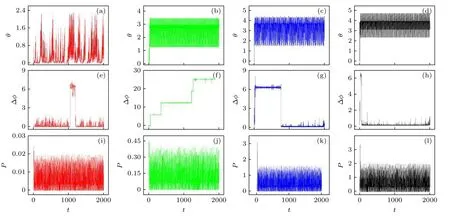
圖7 誤差函數、相位差和功率隨時間的演化(ua = 0.1) (a), (e), (i) I0 = 0.01; (b), (f), (j) I0 = 0.2; (c), (g), (k) I0 = 0.8; (d), (h),(l) I0 = 1Fig.7.Evolution of error function, phase difference and power (ua = 0.1): (a), (e), (i) I0 = 0.01; (b), (f), (j) I0 = 0.2; (c), (g),(k) I0 = 0.8; (d), (h), (l) I0 = 1.

圖8 系統誤差與相位差隨時間的演化(ua = 0.5) (a), (e) I0 = 0.01; (b), (f) I0 = 0.2; (c), (g) I0 = 0.8; (d), (h) I0 = 1Fig.8.Evolution of error function and phase error (ua = 0.5): (a), (e) I0 = 0.01; (b), (f) I0 = 0.2; (c), (g) I0 = 0.8; (d), (h) I0 = 1.

圖9 耦合系統中神經元的ISI 和放電序列(f = 0.002) (a) ua = 0.01; (b) I0 = 0.5, ua = 0.01; (c) I0 = 1.5, ua = 0.01; (d) I0 =0.3; (e) ua = 0.5, I0 = 0.3; (f) ua = 1.5, I0 = 0.3Fig.9.ISI and the firing sequence of neuron in the coupled system (f = 0.002): (a) ua = 0.01; (b) I0 = 0.5, ua = 0.1; (c) I0 = 1.5,ua = 0.1; (d) I0 = 0.3; (e) ua = 0.5, I0 = 0.3; (f) ua = 1.5, I0 = 0.3.

從圖8 可以看出, 改變I0和ua對耦合系統的完全同步沒有貢獻.以上結果與圖6 一致, 在討論的參數范圍內, 混沌放電的FHN 神經元經由光電管耦合情況下,I0較小時由于受迫共振可完全同步;I0較大時趨于相位同步, 此時光電管具有較強的調節能力.

3.2 簇放電FHN 神經元的光電管耦合(f =0.002)

根據(6)式所示的耦合系統, 考慮頻率f=0.002 情況(case 3, 4)下, 耦合系統隨I0和ua變化的峰峰間隔圖(ISI), 如圖9 所示.

圖9 結果表明,I0和ua變化不會改變系統的放電模式, 但對其譜特征會產生影響.如圖9(b)和圖9(c)所示, 在外界激勵U相同的情況下,I0的變化對系統簇放電狀態的影響較大; 而ua對系統簇放電狀態的影響不大, 如圖9(e)和圖9(f)所示.類似3.1 節, 對于第三種情況(case 3), 計算了參數空間中的最大誤差函數θmax與最大相位差Δφmax.

如圖10 所示, 類似混沌放電的情況, 在f=0.002 的情況下, 當I0和ua較小時系統趨于同步,隨著參數I0的增加系統出現去同步現象; 但是參數I0對相位同步的影響較為復雜.以下考慮I0較小的情況, 該區域系統的最大誤差函數和最大相位差均具有下界, 如圖11 所示.

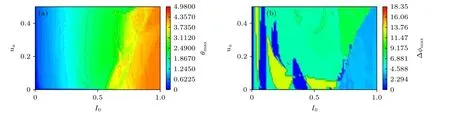
圖10 ua 和I0 的參數空間中, 耦合系統(case 3)的同步區間 (a)最大誤差函數θmax; (b)最大相位差ΔφmaxFig.10.Synchronization region of the coupled system (case 3) in the parameter space of ua vs.I0: (a) Maximum error function θmax;(b) maximum phase difference Δφmax.

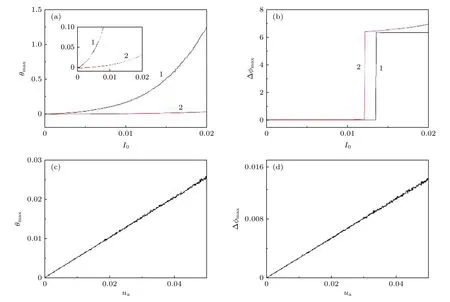
圖11 最大誤差函數和最大相位差隨參數的變化(灰色曲線為(6)式中的非線性耦合, 紅色曲線為線性耦合) (a), (b) ua =0.01; (c), (d) I0 = 0.001Fig.11.The maximum error function and the maximum phase difference change with the parameters, the grey curve represents the nonlinear coupling in Eq.(6) and the red curve is the linear one: (a), (b) ua = 0.01; (c), (d) I0 = 0.001.

圖11 (a)和圖11(b)分別計算了相應參數下非線性耦合(曲線1)和線性耦合(曲線2)的情況, 結果表明, 在耦合強度較小, 即I0< 0.01 時在有限的單位時間內系統誤差峰值可以減小到零附近, 耦合系統具有可以實現完全同步的趨勢; 而且不同于誤差函數曲線的“軟擊穿”特性, 相位差函數表現為“硬”的, 但是沒有觀察到亞臨界分岔, 且相對誤差函數的閾值顯著滯后.此外, 線性耦合方式增大了可同步的參數I0區間, 減小了相位同步的參數I0區間.如圖11(c)和圖11(d)所示, 不能區別線性和非線性耦合下最大誤差函數和最大相位差隨ua變化的關系曲線; 而且相對最大誤差函數, 最大相位差的增長更加緩慢.I0和ua的增強去同步可以理解為受迫共振效應與(線性或非線性)耦合系統的競爭關系; 當受迫共振效應強于耦合作用時,表現為同步現象; 否則由于自突觸、光電耦合等結構影響, 系統會遠離同步狀態.具體參數下耦合系統間的誤差、對應的相位差和光電管功率的計算結果如圖12 所示.

如圖12(a)、圖12(c)、圖12(e)和圖12(g)所示, 較小的I0促進耦合系統間的同步; 增大I0, 耦合系統出現間歇性完全同步, 可能是過量的能量注入引起的, 如圖12(d)和圖12(h)所示.此外,圖12(i)—(l)是對應參數下光電管的功率變化, 可以看出, 當I0繼續增大時, 光電管通過光吸收調節系統能量的能力增強.這與典型的線性反應-擴散系統的情況一致.對于第四種情況(case 4), 具有較大的ua(ua= 0.5)時耦合系統間的誤差及對應的相位差結果如圖13 所示.

從圖13 可以看出, 具有較大的ua時改變I0的大小無法促進耦合系統間的完全同步和相位同步; 對比圖12 和圖13,I0相同的情況下,ua大的系統較難實現完全同步和相位同步.本文計算結果表明, 對于尖峰放電(f= 0.012)和周期放電(f=0.06)的FHN 神經元, 可能是由于與簇放電同屬于周期態放電, 因此I0和ua對同步的影響相似.

圖12 系統誤差、相位差和光電管功率隨時間的演化(ua = 0.01) (a), (e), (i) I0 = 0.001; (b), (f), (j) I0 = 0.01; (c), (g), (k) I0 =0.013; (d), (h), (l) I0 = 0.014Fig.12.Evolution of error function, phase error and phototube power (ua = 0.01): (a), (e), (i) I0 = 0.001; (b), (f), (j) I0 = 0.01; (c),(g), (k) I0 = 0.013; (d), (h), (l) I0 = 0.014.

圖13 系統誤差與相位差隨時間的演化(ua = 0.5) (a), (e) I0 = 0.001; (b), (f) I0 = 0.01; (c), (g) I0 = 0.013; (d), (h) I0 = 0.014Fig.13.Evolution of error function and phase error for variables (ua = 0.5): (a), (e) I0 = 0.001; (b), (f) I0 = 0.01; (c), (g) I0 = 0.013;(d), (h) I0 = 0.014.

從物理過程來看, 外界光照激勵時耦合通道的光電管主要扮演非線性電阻角色, 即在兩個神經元電路之間觸發非線性耦合并消耗一定的能量, 從而平衡兩個耦合電路的能量以及輸出電壓.從動力學和實驗的角度看, 對光電管的參數或耦合通道參數進行調制, 就可以實現兩個神經元電路的同步.當嵌入耦合通道的光電管被處于紅限頻率以上的光照激活后, 光電管則發揮調變電源的作用, 對耦合神經元電路注入能量, 進一步改變其動力學特性,在恰當的參數范圍內實現神經元電路的同步和相位鎖定.從實驗角度看, 改變外界光照強度則可以調控耦合通道光電流大小, 進一步改變耦合神經元電路的輸出電壓特性和動力學模態, 對同步穩定性產生顯著影響.

4 結 論

本文基于光電管耦合FHN 神經元電路, 研究了影響神經元系統同步動力學的因素.耦合FHN神經元的光電管作為電流源, 可通過調節光照強度改變光電流大小; 數值計算表明, 由于光電管能量的注入以及能量的調節和輸運, 處于混沌放電模式的神經元在較強的耦合強度也能相位鎖定或相位同步.在光電管耦合的(多)周期放電的神經元(包括簇放電、尖峰放電和周期放電)中, 相位同步的區間更加復雜.在相同耦合強度下, 具有較大反向截止電壓的光電管耦合的神經元不能實現同步及鎖定, 這是因為反向截止電壓大的情況下, 光電管需要吸收更大的能量才能實現對系統能量的注入,從而使耦合系統實現相位同步.