函數在高等數學教學中的應用
2021-05-15 04:06:00張學福
河西學院學報 2021年2期
張 學 福
(河西學院數學與統計學院,甘肅 張掖 734000)
在概率統計和工程技術中,經常遇到下述形式的含有參數α 的廣義積分
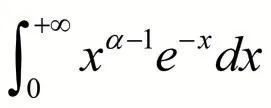
可以證明,當α >0 時,該積分收斂,積分值隨α 的變化而變化,稱之為Γ 函數[1],記作Γ(α),即

此函數的學習和在概率統計及工程技術中的應用,教學中受知識梯度和認知水平的影響,一般安排在一元函數的廣義積分計算、極坐標下二重積分的計算和概率統計教學中分別進行.受教學時間跨度長、知識點零散、銜接不緊密等影響,在知識掌握和應用上顯得系統性不強、效果不佳.所以有必要對其性質和重要結論以及各種應用作以歸納總結,使其零散的教學內容系統完整,分段掌握的知識能夠形成一個整體,同時展示Γ 函數在概率統計和工程技術中的應用和彰顯Γ 函數計算一類反常積分方便、快捷的優勢.
1 Γ 函數收斂性

2 Γ 函數性質
2.1 遞推公式
Γ(α+1)=αΓ(α)(α >0),由分部積分法容易得到

一般地,對任何正整數n,有
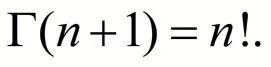
因此,Γ 函數可以看成是階乘n!的推廣.
2.2 當α →0+時,Γ(α)→+∞. (Γ 函數在α >0 時連續)
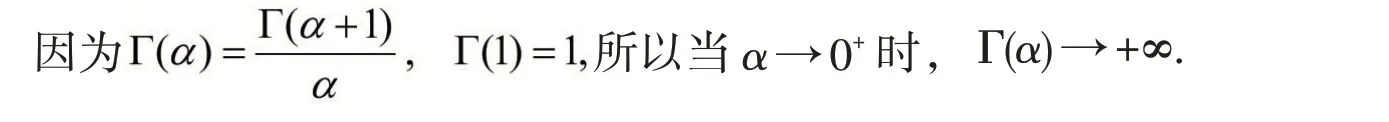
2.3 余元公式[2]

在Γ 函數的定義式中,令x=t2,則有


3 Γ 函數的應用
3.1 計算反常積分
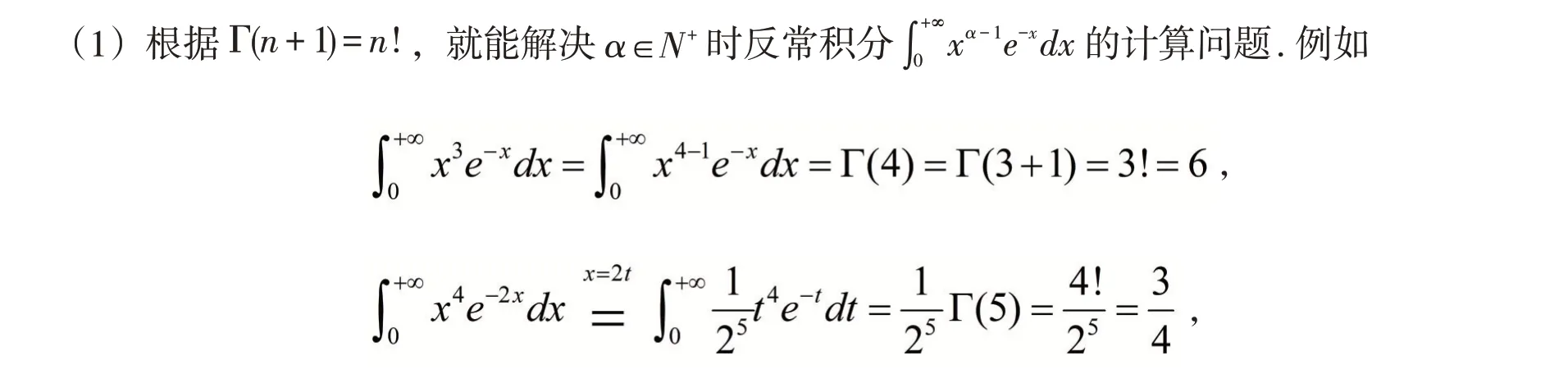
等等.

3.2 計算概率論中隨機變量分布中參數、數學期望及方差
例1 設隨機變量X 服從麥克斯韋分布[4],其密度函數為

解 由概率密度函數的性質知

代入已知條件得

其中σ >0 是常數,求E(x)和D(x).

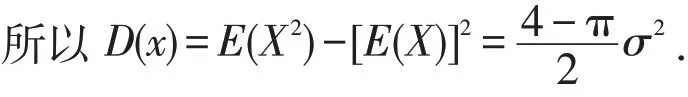
3.3 數理統計的幾個常用分布中的應用
(1) χ2分布
設n 個隨機變量X1,X2,…,Xn相互獨立,且都服從標準正態分布,可以證明函數


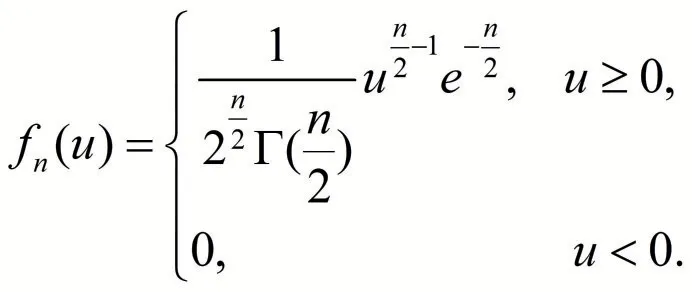
的概率密度為以上三種分布中的概率密度所含的廣義積分都可歸結為Γ 函數的計算.
猜你喜歡
數學雜志(2021年6期)2021-11-24 11:12:00
中學生數理化(高中版.高二數學)(2021年5期)2021-07-21 02:14:46
數學年刊A輯(中文版)(2021年1期)2021-06-09 09:31:56
中等數學(2020年6期)2020-09-21 09:32:38
甘肅教育(2020年14期)2020-09-11 07:57:50
甘肅教育(2020年12期)2020-04-13 06:25:34
中等數學(2019年6期)2019-08-30 03:41:46
中學生數理化·七年級數學人教版(2018年4期)2018-06-28 03:26:30
東方教育(2017年19期)2017-12-05 15:14:48
唐山文學(2016年2期)2017-01-15 14:03:59

