利用圓的性質解決力學中動態平衡問題
何 勇 任致遠
(新疆兵團二中,新疆 烏魯木齊 830002)
高中物理無論是力學、熱學,還是電學中,動態平衡問題會被經常用來考查學生對物理問題理解能力、知識遷移能力,分析推理能力、綜合運用能力和利用數學知識解決物理問題的能力.在力學問題中動態平衡,我們往往常用的有圖解法和解析法.這里我們將利用圓的相關性質,結合“三角形相似”、“正弦定理”和“輔助圓”解決一些與圓相關的動態平衡問題.
1 利用三角形相似處理動態平衡
例1.如圖1所示,固定在豎直平面內的光滑圓環的最高點有一個光滑的小孔.質量為m的小球套在圓環上.一根細線的下端系著小球,上端穿過小孔用手拉住.現拉動細線,使小球沿圓環緩慢上移.在移動過程中手對線的拉力F和軌道對小球的彈力N的大小變化情況是

圖1
(A)F不變,N增大. (B)F減小,N不變.
(C)F不變,N減小. (D)F增大,N減小.
在本題中,小球沿圓環緩慢上移,對小球進行受力分析時,我們發現它始終受到豎直方向重力G、沿細繩方向拉力F和沿圓半徑方向彈力FN,這3個力滿足受力平衡.作出受力分析圖(圖2),可知△OAB∽△GF′A
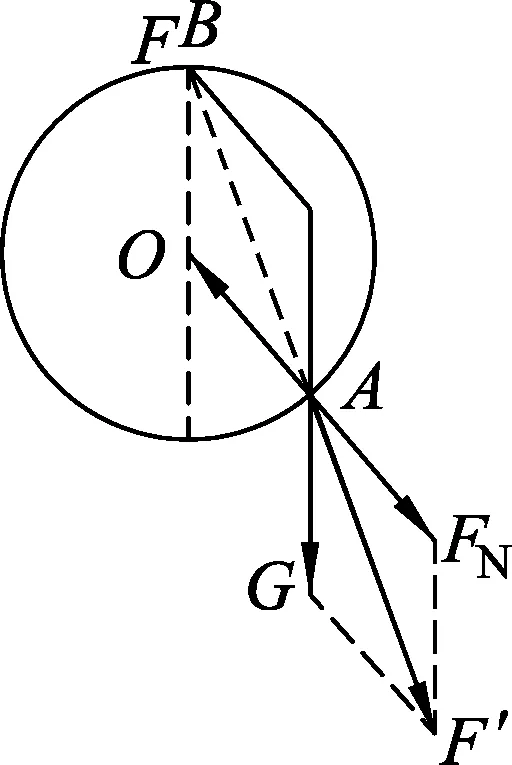
圖2
在重力G,圓的半徑R不變時;小球緩慢上移過程中,l逐漸變小,所以F逐漸減小.
2 利用正弦定理處理動態平衡
例2.如圖3所示,ADB是一個光滑球面,AOB為水平直徑,C為質量為m的光滑小球,小球通過過A點處的光滑定滑輪的輕繩拉住,現使小球C緩慢地從A點運動到處于O點正下方的D點處.重力加速度大小為g,關于小球C從A點運動D點的過程,下列說法正確的是
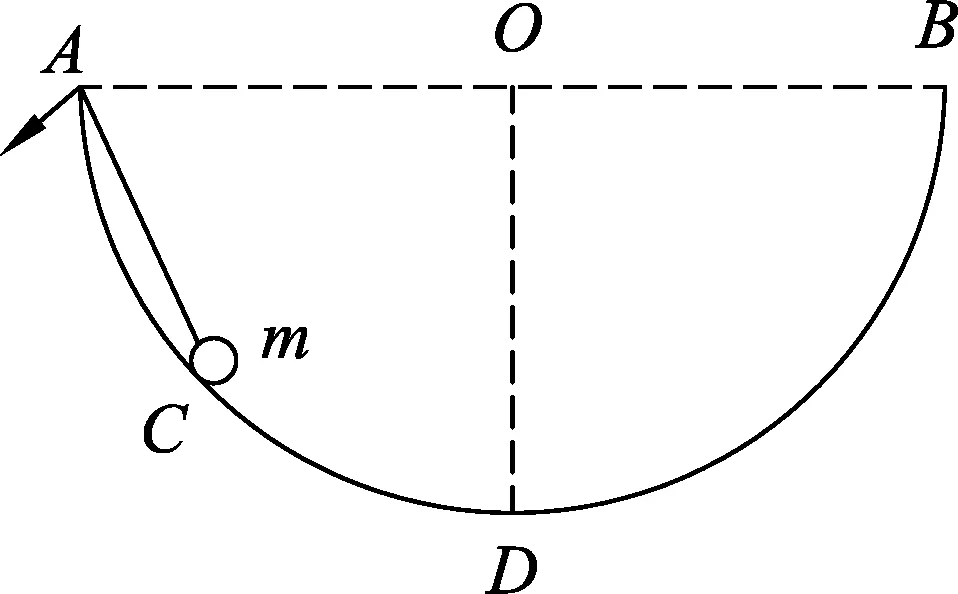
圖3
(A) 繩對小球的拉力先增大后減小.
(B) 繩對小球的拉力逐漸減小.
(C) 光滑球面對小球的支持力先減小后增大.
(D) 光滑球面對小球的支持力逐漸減小.
在本題中,小球沿圓環緩慢上移,如圖4,對小球進行受力分析時,我們發現它始終受到豎直方向重力G、沿細繩方向拉力F和沿圓半徑方向彈力N,這3個力滿足受力平衡.

圖4
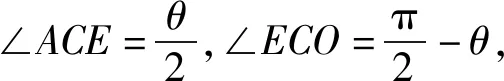
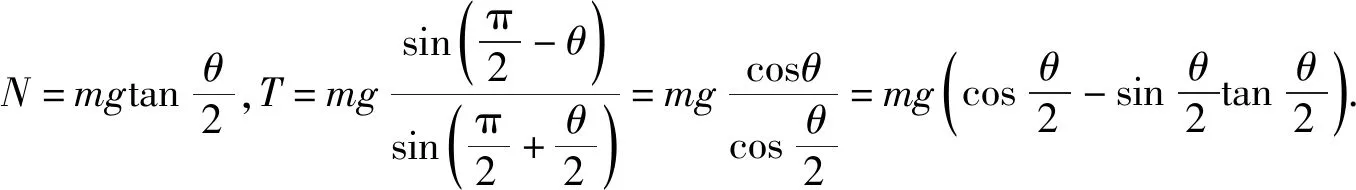
3 利用輔助圓通過圖解法處理動態平衡

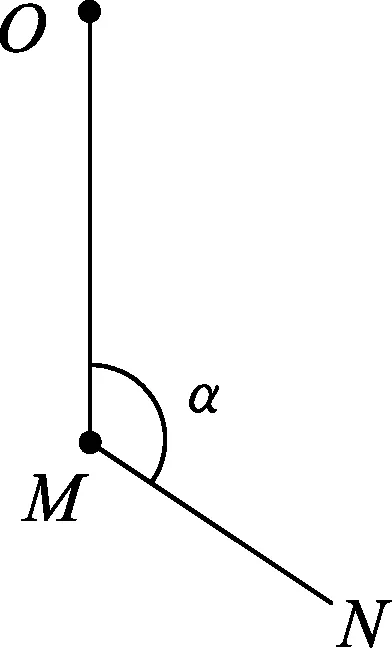
圖5
(A)MN上的張力逐漸增大.
(B)MN上的張力先增大后減小.
(C)OM上的張力逐漸增大.
(D)OM上的張力先增大后減小.
對M處的重物進行受力分析,并將力平移至一個力的三角形中,如圖6所示,重力大小方向不變,其所對的角為π-α也始終不變,作出這個三角形的外接圓,三力平衡構成封閉三角形,畫其外接圓,利用圓周角不變解題.P在外接圓上移動,初始位置從重力末端直至圖中Q點,利用圖解法確定力FNM及FOM的變化情況.
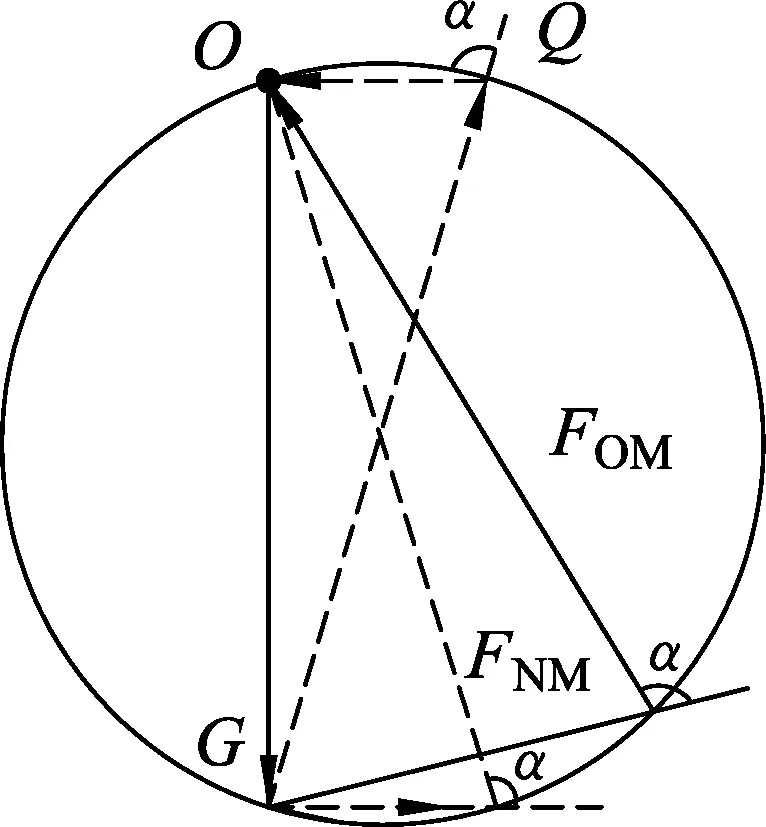
圖6
下面我們就3種方法來解決一個力學中動態平衡的問題.
應用:如圖7所示為一種兒童玩具,在以O點為圓心的四分之一豎直圓弧軌道上,有一個光滑的小球(不能視為質點),O′為小球的圓心.擋板OM沿著圓弧軌道的半徑,以O點為轉軸,從豎直位置開始推著小球緩慢順時針轉動(水平向里看),到小球觸到水平線的過程中:圓弧軌道對小球的支持力N1的變化?擋板對小球的支持力N2的變化?
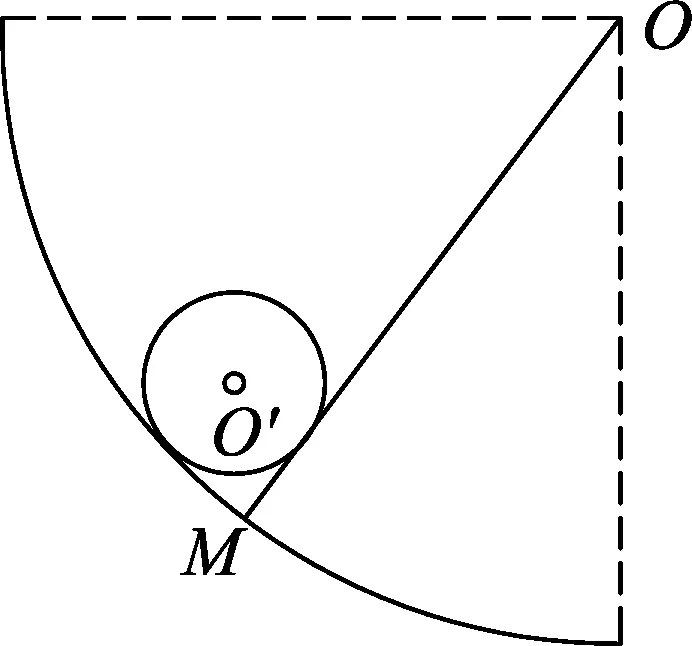
圖7
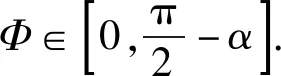
解法1:利用三角形相似(此法關鍵在于找到與受力三角形相似的三角形)延長N2作用力力線,交豎直線ON于A點,OM于B點,
根據圖8受力的三角形與△OO′A相似,可得以下關系
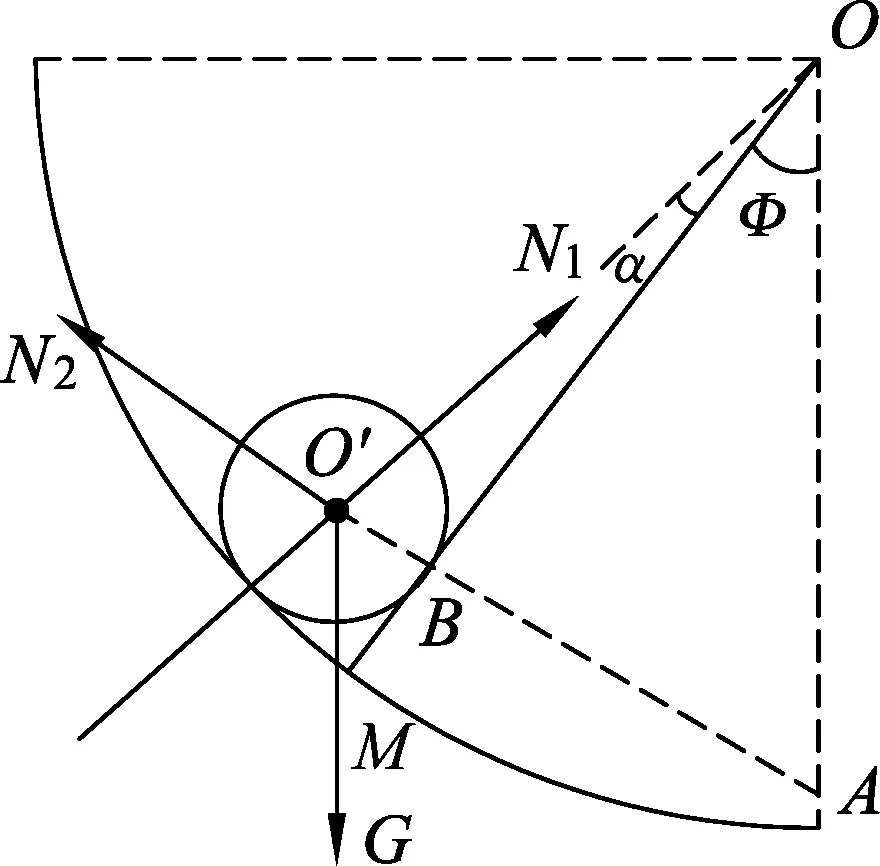
圖8
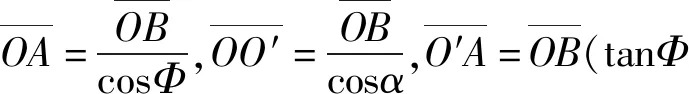
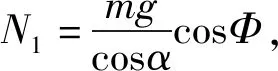
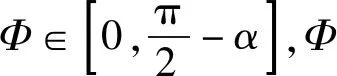
解法2: 利用正弦定理(此法關鍵在于找到與受力三角形,確定各力間的夾角)
根據圖9力的三角形中邊和對應角,由正弦定理可得
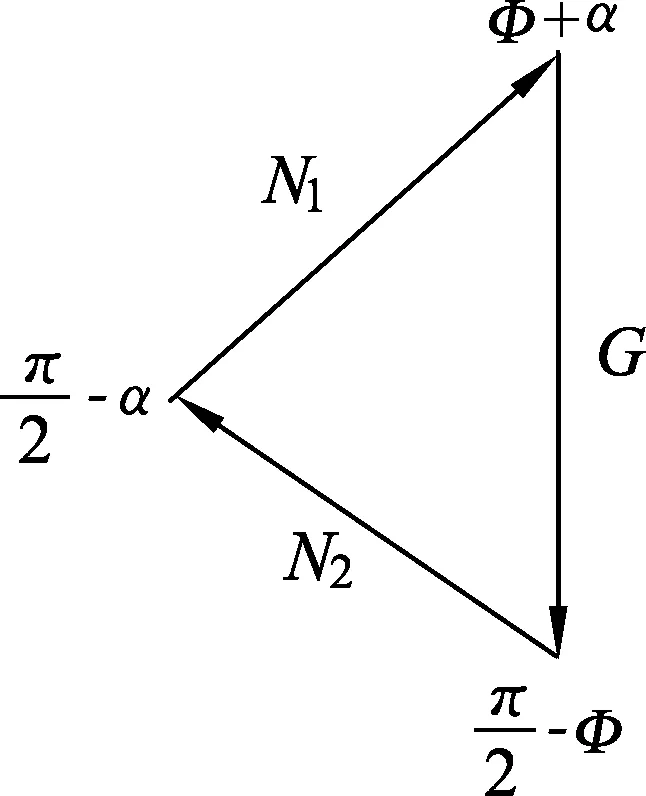
圖9
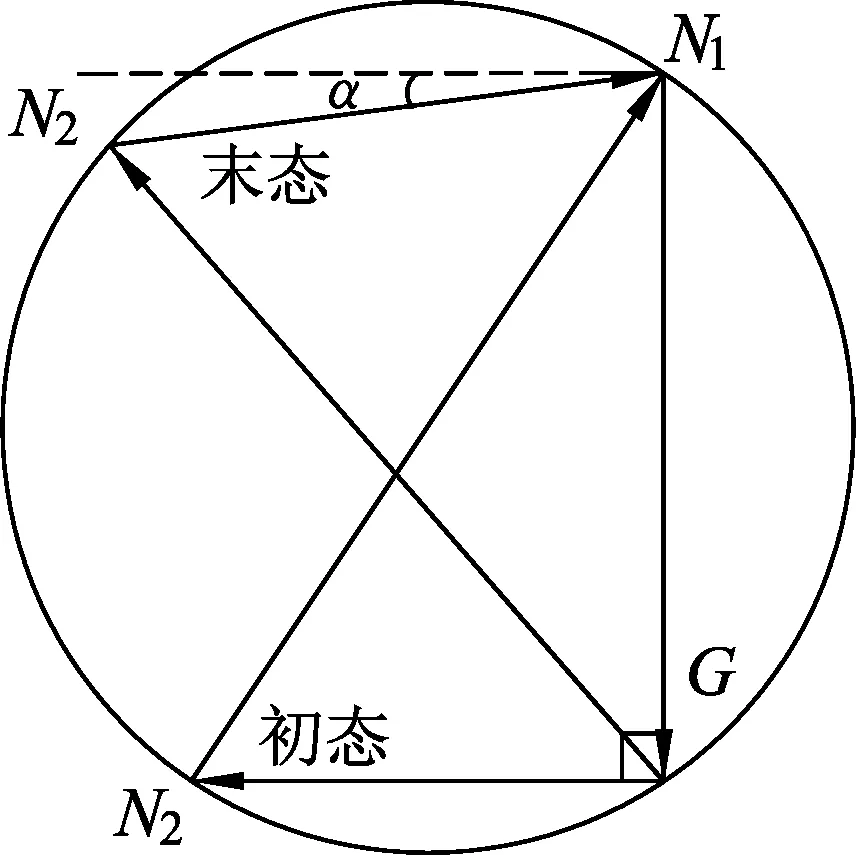
圖10

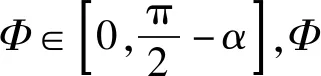
解法3:利用輔助圓通過圖解法處理動態平衡
(此法關鍵在于中間有兩個力的夾角必須不變)
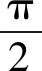
以上幾種利用圓的性質和特點,解決力學中的動態平衡問題的方法,有時也是相通的.在教學和考試中,只要把握住其中的關鍵信息和條件,指導學生選擇適合自己理解的方法,都可以達到事半功倍的效果.

