圓盤錯流過濾黑液截留木質素數值模擬研究

杜鐘雨 吳俊飛 趙文捷

（青島科技大學機電工程學院）

木質素作為一種大量存在的可再生資源，具有巨大的應用潛力，工業木質素主要來源于制漿造紙工業和木材水解工業［1］，通過過濾機過濾制漿黑液得到。 傳統的過濾機理是濾液垂直于過濾介質的表面流動，固體被過濾介質截流，小顆粒通過過濾介質，大顆粒則被留在膜上達到過濾效果。 但是，隨著過濾的進行，濾膜上會有固體物質堆積形成“濾餅”，且隨著“濾餅”厚度逐漸增加，過濾速度會急劇降低，在過濾時需要進行人工排渣。 所以傳統過濾必須使用絮凝劑或助濾劑［2］。

動態錯流過濾是一種全新的過濾系統，原料液在壓力泵的作用下， 通過進口進入濾室中，并一級一級地往下過濾。 由于濾膜的過濾作用，濾液通過濾膜時大顆粒被截留在濾膜上。 另外，在濾室中設置了連續轉動的轉子，使原料液產生旋流。 隨著過濾的進行，原料液逐漸變濃，在過濾機的最末端，物料的濃度達到最高，這時就需要進行人工卸料。 動態錯流過濾機廣泛用于懸浮物的連續過濾和濃縮，過濾壓力通常為0.4～0.6MPa；固體濃度可高達80%以上［3］。 通過研究，相對于傳統的交叉流過濾，旋轉圓盤過濾能產生更高的滲透通量和更好的溶質傳輸，因為它們在膜上產生的高剪切速率可以防止或限制“濾餅”的形成，而且高剪切速率和跨模壓（TMP）的結合促進了大分子在膜上的傳輸［4］。

動態過濾機作為一種新型的過濾設備，自問世以來，受到國內外學者的廣泛關注，并對過濾機的設備和過濾理論方面進行大量的實驗和模擬研究。

日本學者Shirato于1986年首先研究了沒有過濾過程、沒有流體流入條件下，層流狀態時的流體切向速度；1991年Yamaznki等在Shirato研究的基礎上又對相同條件下湍流狀態時流體切向速度的表達式進行了研究，且對牛頓型流體和非牛頓型流體進行了對比研究［5］。然而在實際操作中，旋轉壓濾機是有過濾過程和有濾液流入的，所以日本學者的研究與實際操作狀態不符。

文獻［6］中研究了層流狀態（雷諾數Re＜104）濾室內的流體過濾機理與流體的流速、剪應力和過濾速率的關系，在理論上進行初步討論，但是只停留在有單面過濾、有流量的情況下。 天津大學課題組通過分析濾室內流體的流動機理，建立了數學模型并得到了實驗驗證，形成了一套濾室內流體流速的理論計算方法。

1996年，譚蔚等通過探針和激光多普勒測速系統測定了在不同條件下的切向速度并分析得出幾個結論：濾室進口處的流量大小對進口兩側流體切向速度的影響呈相反趨勢；流體的切向速度隨著圓盤轉速的增加而增加；通過分析給出了低濃度物料過濾面上的平均過濾速率表達式［7］。

近年來，如何提高壓濾機的效率、減少功耗成了該領域的熱點問題。 壓濾機的過濾效率取決于濾室內的流場分布，而流場分布則直接受到圓盤轉子高速運轉形成的力場的影響，這與圓盤轉子的轉速及其與膜之間的間隔有著十分密切的關系。筆者將利用CFD軟件Fluent對不同轉速的圓盤轉子壓濾機濾室內部的流場進行模擬，可以避免實驗條件和各種因素的限制， 得到特定轉速、跨膜壓作用下剪切速度和轉子動壓力的有效數據，為以后的研究積累經驗。

1 濾室內部流體流動控制方程

濾室內部流體的流動要受到物理守恒定律的支配， 基本的守恒定律包括質量守恒定律、動量守恒定律和能量守恒定律。 對于本課題中的不可壓縮流體，整個過程熱交換可以忽略，所以能量守恒定律可以不考慮，只考慮質量守恒定律和動量守恒定律。

任何流動問題都要遵循質量守恒定律，可以表述為： 單位時間內流體微元體中質量的增加，等于同一時間間隔內流入該微元體的凈質量。 因此可以得到質量守恒方程為：

該方程同時適用于可壓縮流動和不可壓縮流動。 Sm是從分散的二級相中加入到連續相的質量，當然也可以是任何自定義源相。

任何流動系統都要遵守動量守恒定律，可以表述為：微元體中流體的動量對時間的變化率等于外界作用在該微元體上的各種力之和。 因此可以得到動量守恒方程為：

2 計算模型的建立

2.1 幾何模型的建立

如圖1所示， 使用NX-UG完成一級濾室的三維模型建立。In和Out分別表示黑液進口和濾液出口。 其中圓盤轉子與膜的距離C=15mm，圓盤的直徑D=128mm，濾室的直徑T=137mm，濾室的厚度H=30mm。 濾室模型正等軸測圖如圖2所示。

圖1 一級濾室幾何模型尺寸標注

圖2 濾室模型正等軸測圖

2.2 數值模型的建立

在NX-UG中創建濾室和旋轉圓盤的三維模型，考慮到Fluent中選用MRF（多重參考系）模型進行計算， 所以對整個模型進行動靜區域劃分，此步驟直接在UG中使用求“減”運算來完成。在整個濾室內建立一個圓柱塊體將整個圓盤包住作為動區域，整個濾室內充滿黑液作為靜區域。 這個圓柱塊體的外表面設置成一對相對應的Interface，作為能量傳輸界面，使得動區域轉子產生的旋流能夠影響到靜區域。 另外，在濾室的出口附近建立一個多孔介質區域，同理，多孔介質區域外邊界也為一對Interface作為能量的傳輸界面。因為圓盤內部不參與流場計算且不考慮傳熱等，所以直接求“減”運算且不保留工具體，圓盤只保留一個外殼形狀的面，后續邊界條件設置直接將之設置為Wall。 然后再次對圓柱體、 多孔介質區域和整個濾室腔做“減”運算，并保留工具體，目的是為了在動區域和靜區域中都有一個可以選擇的面定義為一對Interface。

完成三維模型的建立之后將之另存為Parasolid（.x_t）格式的文件并導入Workbench Mesh進行網格劃分， 將導入模型的3個body重命名為liquid、swirl-area、membrane， 分別代表黑液區、動區域和膜。 劃分的網格數為651 023，質量檢測良好，平均質量為0.81。整體網格劃分如圖3所示；具體的分區如圖4所示； 圓盤和濾膜區域進行了網格加密（圖5）。

圖3 整體網格劃分

圖4 邊界類型及分區示意圖

圖5 圓盤及濾膜區域網格劃分

2.3 邊界條件設置

使用Fluent對濾室內部的流場進行模擬，基于常用的壓力與速度耦合的SIMPLE算法，SIMPLE算法的核心思想可以概括為：給定壓力場，求解離散形式的動量方程，從而得到速度場，與本模擬相吻合。模型選用RNG k-ε模型，該模型計算速度梯度較大的流場時精度更高，且考慮到旋流效應，對旋轉流動計算精度有所提高，因此更加適用于本旋流模型。 材料物性設置中，黑液的密度設置為1 098kg/m3，粘度為5.85mPa·s。邊界條件設置中， 入口類型為進口壓力， 分別為0.5、1.0、1.5、2.0bar（1bar=0.1MPa）。 出口類型為壓力出口，壓力為零。

旋轉圓盤設置為Wall邊界條件， 分別以300、800r/min的速度旋轉， 旋轉類型設置為Moving Wall，且與鄰近單元相對轉速為零，實現與周圍流體同步運動，不存在相對運動。

旋轉流體區Swirling-Area： 在運動類型中選擇多重參考系MRF模型，運動方式為轉動，旋轉速度分別為300、800r/min。 旋轉方向為繞z軸正方向。

Liquid區域同樣選擇MRF模型， 運動方式相對于動區域運動，旋轉方向為z軸正方向。

2.4 多孔介質區域設置

因為流場中存在濾膜，設置邊界時就需要使用多孔介質條件，以提高計算精度。 多孔介質模型的動量方程就是在標準動量方程的基礎上加了源項Si， 這個源項包括粘性損失項和慣性損失項，即：

2.5 假設條件

在整個濾室內部，湍流流場很復雜，需要對其中幾個條件進行假定：黑液在濾室內部做定常且不可壓縮流動，且整個過程為恒溫過程；文中的研究對象是壓濾機的一級濾室，所以混合物濃度相對較低，可以忽略液固相之間的相互作用力。

3 模擬結果及討論

由Fluent通過后處理可以得到圓盤轉子動壓力云圖和膜表面的速度矢量圖，結論中主要觀察了圓盤轉子的轉動引起的膜剪切速度的變化和轉子動壓力的變化。

3.1 圓盤轉子動壓力的變化

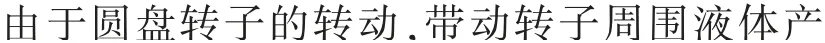
圖6 轉速為300r/min時圓盤轉子的動壓云圖

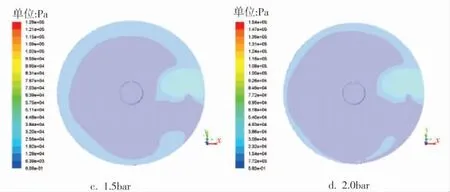
圖7 轉速為800r/min時圓盤轉子的動壓云圖

根據動壓變化散點圖（圖8）可知，當轉速為300r/min時，此時的動壓最大為949Pa（0.5bar條件下），最小為606Pa（1.5bar條件下）；當轉速增大為800r/min時，動壓數值隨進口壓力的增大而增大。0.5bar 時 動 壓 達 到 了6 162Pa，2.0bar 時 最 大 為7 643Pa。計算得知，相同進口壓力條件下，800r/min時要比300r/min時的動壓力高很多， 最高相差12倍。 另外，根據圖8可以很清晰地發現，300r/min、0.5bar時的動壓為4個壓強下最大； 而800r/min、2.0bar時的動壓為4個壓強下最大。

圖8 不同壓力下動壓變化散點圖

3.2 膜附近流場剪切速度的變化

膜附近流場的變化，直接受到圓盤轉速的影響。 另外，Interface界面的定義也保障了動區域、靜區域和膜區域之間的能量傳輸，保證圓盤旋轉產生的力場直接影響到膜附近的流場。 通過Fluent后處理可以得到流場的剪切速度矢量圖，筆者截取了距離濾膜最近的z=2mm的等值面作為目標面，查看流場的剪切速度變化。

由兩個速度矢量圖（圖9、10）可以看出，剪切速度沿膜半徑的增大而增大， 由圖9、10可以得知，當圓盤轉速為300r/min時，目標面的剪切速度最大達到1.29m/s， 而當轉速增大到800r/min時，4個進口壓力下最大剪切速度達到3.70m/s。 同樣進口壓力作用下剪切速度是300r/min時的2.8倍左右。 另外，由兩個散點圖（圖11）不難看出，轉速較低時，剪切速度隨著進口壓力的增大而呈現逐漸減小的趨勢，且進口壓力的變化對于剪切速度的影響相對較明顯；轉速較高時，剪切速度隨著進口壓力的增大而增大，進口壓力的變化對剪切速度的影響較小。

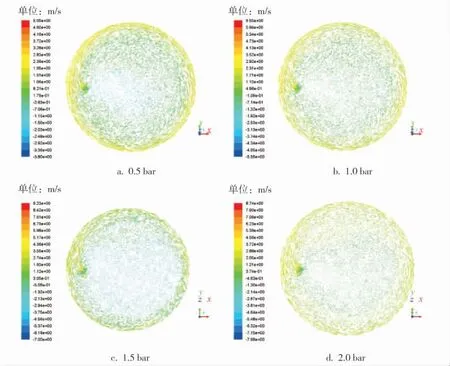
圖9 轉速為300r/min時膜上剪切速度矢量圖

圖10 轉速為800r/min時膜上剪切速度矢量圖

圖11 不同壓力下剪切速度變化散點圖

4 結論

4.1 用Fluent軟件對圓盤錯流過濾機的一級濾室進行流場模擬，分別模擬了圓盤轉速為300r/min和800r/min時不同跨膜壓作用下的流場情況，當圓盤轉速為300r/min時， 圓盤動壓力在1.5bar時進口壓力下最小，為600Pa，在0.5bar時最大，為949Pa；而當轉速為800r/min時，隨著進口壓力設置參數逐漸增大而增大。 相同進口壓力條件下，800r/min時要比300r/min時的動壓力高很多，最高相差12倍。

4.2 當圓盤轉速為300r/min時，4種進口壓力條件下剪切速度最大值的下降趨勢為0.5bar>1.0bar>1.5bar>2.0bar，最大達到1.29m/s；當轉速為800r/min時，4種進口壓力條件下剪切速度最大值的下降趨勢為2.0bar>1.5bar>1.0bar>0.5bar， 最大達到3.70m/s；轉速較低時，進口壓力的變化對于剪切速度的影響相對較明顯。