面向運營隧道結構健康監測系統大數據壓縮感知研究

吳賢國，鄧婷婷，陳 彬，*，曾鐵梅，陳虹宇，張凱南

(1.華中科技大學土木與水利工程學院，湖北 武漢 430074；2.武漢地鐵集團有限公司，湖北 武漢 430030；3.新加坡南洋理工大學土木工程與環境學院，新加坡 639798)

0 引言

近年來，隨著地下交通運輸系統的迅猛發展，基于多節點傳感器網絡的地鐵損傷識別及健康監測系統逐步得到應用，監測數據采集、傳輸、存儲和處理成本的消耗是傳感器網絡系統搭建的一個關鍵性技術問題。傳統的信號采集方法基于Nyquist采樣定律，為了避免信號恢復的損耗，響應采集頻率需大于原始響應最大頻次的2倍，給數據的傳輸和存儲帶來沉重的負擔，如何在保證重構精度的情況下盡可能地減少數據量是地鐵健康監測系統數據采集與傳輸領域面臨的新挑戰。

隨著信號采集重構問題的出現，Donoho[1]、Candes等[2]提出了壓縮感知理論的基本原理，并將壓縮感知理論分為信號稀疏化、選取測量矩陣和信號重構算法3個主要部分。其中，測量矩陣將稀疏信號從高維空間投影到低維空間上，解決了傳統采樣方法數據存儲壓力大、采樣時間長的問題[3]。由于測量矩陣決定了采樣信息的壓縮性能與恢復質量，其構建成為了壓縮感知研究的熱點[4]。Bajwa等[5]提出構建Toeplitz隨機矩陣，簡化了測量矩陣的結構和尺度。趙貽玖[6]對隨機等效采樣技術的隨機相位產生機制進行了分析。Yang等[7]基于圖像先驗以及條件約束來設計最佳的自適應測量矩陣。Wu等[8]將測量的耦合值作為邊界條件來求解Laplace′s方程，得出的自適應測量矩陣能夠較好地平衡處理次數與處理精度。趙玉娟等[9]基于隨機高斯矩陣稀疏系數的部分向量進行自適應變換，構建的測量矩陣使重構的信號有更高的精度。綜上所述，合適的測量矩陣能夠降低壓縮感知的計算量，并能提高信號重構的精度，在研究壓縮感知問題時，需要選擇與信號特點相匹配的測量矩陣以提高計算效率。

信號重構算法是壓縮感知3個主要部分的關鍵環節。目前主流的信號重構算法包括貪婪迭代算法、LS算法以及基于貝葉斯模型的重構算法[10]。貪婪迭代算法最早由Davis等[11]提出，隨后針對提高計算速度和計算精度等執行性能成為了研究熱點。Tropp[12]提出了正交匹配追蹤算法。基于此，為了得到更快的計算速度，Gavish等[13]基于傳統匹配追蹤算法的初始參數，采用精簡化推出分段正交算法，并運用于大數據領域的實際工程。與此同時，一些學者依據壓縮感知稀疏重構模型將其轉化為凸優化問題求得原始信號的近似解，基于此最早提出了基追蹤算法[14]，同時也提出了稀疏梯度投影模型[15]、基于平滑L0范數的算法模型[16]、最小化L1范數求解稀疏模型[17]等重構算法。目前，壓縮感知理論受到業界學者廣泛的研究，研究方向涉及圖像壓縮重構[18]、聲道信號處理[19]、檢測報警系統[20]等信號大數據領域，但在土木工程行業應用涉及較少，方法也較為傳統[21]，缺少針對運營隧道結構健康監測特點的壓縮感知方法。針對運營隧道監測中大數據傳感器網絡監測量結構性差、盲稀疏度、高噪聲干擾的特征，將壓縮感知理論引入運營隧道結構健康監測中的數據采集和傳輸層，結合隧道工程運營期監測數據的特征降低采樣率，減少數據采集過程中的資源浪費和服務器無線傳輸負擔。

本文研究基于傳統單節點壓縮感知重構算法，引入傳感器網絡框架表示模型，對傳統的壓縮采樣數據重構算法進行改進，轉化為凸優化問題，用迭代方法求解最小化范數問題，提出基于傳感器網絡的壓縮感知重構算法。以武漢地鐵3號線王家灣至宗關區間(以下簡稱王宗區間)隧道采集的加速度信號為例，對提出的算法進行驗證，對原始信號進行多層次采樣，并采用傳統單節點壓縮感知重構算法和基于傳感器網絡的壓縮感知重構算法進行信號重構，結果表明，基于傳感器網絡的壓縮感知重構算法在一定采樣率條件下可以有效增加數據恢復的精度。

1 面向運營隧道結構健康監測預警系統大數據壓縮感知

1.1 傳統單節點壓縮感知重構算法理論

當前運營隧道健康監測系統中遠程傳感器網絡受計算能力較差、傳輸帶寬低、要求實時傳輸等條件的限制，大都采用基于Nyquist采樣定律的傳統信號采集傳輸方法處理監測數據。傳統信號采樣壓縮過程包括原始信號采樣、量化、壓縮編碼、信號重構。隨著壓縮感知的提出，信號采集處理的過程變為稀疏變換、編碼測量和信號重構。傳統信號采樣壓縮需要對信號均勻抽樣，再對采用的信號量化編碼壓縮降低信號冗雜。壓縮感知的核心是線性測量，壓縮過程即采樣過程，通過少量的采樣信號得到精準的重構信號，降低全過程數據庫的運載消耗。傳統壓縮感知研究主要從信號稀疏化、選取測量矩陣、信號重構算法3方面展開。

1.1.1 信號的稀疏變換

信號的稀疏變換反映的是信號的稀疏性，信號稀疏性定義如下：

假設向量u∈Rm有k個非零元素，且滿足k?m，則u為R上稀疏度為k的稀疏向量。

設有1個一維信號x∈Rn,該信號可以用1組正交基ψ=[ψ1,ψ2,…,ψn]進行線性表示，表達形式如式(1)—(3)所示。

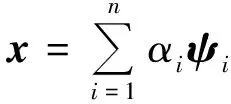
(1)

αi=〈x,ψi〉或α=ψTx。

(2)

ψ=[ψ1,ψ2,…，ψn]。

(3)

式(1)—(3)中：x為原始一維信號；αi為正交基下的分解系數；ψ為信號x∈Rn的正交變換基。

如果x的分解系數αi中有k個非零元素，則信號在ψ正交基上是稀疏的，這也是數據可以被壓縮采樣的基礎，信號稀疏性的不同將在很大程度上影響重構信號的精度。一般來說，結構健康監測過程中采集的信號本身不具有稀疏性，但采集的振動信號可以在某幾組變換基下線性展開，如果變換基線性表示系數僅有少量非零值或是忽略不計的系數，在某種程度上也可以稱信號在相應的變換基上具有稀疏性。信號的稀疏性是信號壓縮采用的前提，信號稀疏性越好，振動信號的壓縮采樣結果越好，最終重構信號精度越高。

1.1.2 測量矩陣的構建

壓縮感知是取1個不同于ψ正交基的測量矩陣Φ∈Rm×n，將稀疏信號x從N維空間通過線性投影到M維空間當中，其中M?N，最后得到1個投影后的測量值，聯合式(4)，過程如下。

y=Φx或y=Φψα。

(4)

式中：y為投影后的測量值；Φ為測量矩陣。

為了使測量值更多地保留原始信號的有效信息，令θ=Φψ,θ需要滿足約束等距性(RIP性質)，即稀疏度為k的原始信號x，如果測量矩陣滿足以下關系，則信號x滿足RIP性質。

(5)

式中δk為等距常數。

矩陣RIP性質的運用雖然保證了測量矩陣的有效性以及較高的重構信號精度，但是驗證矩陣是否滿足約束等距條件需要復雜的計算過程。為簡化問題，根據Candes等[22]提出的可利用觀測矩陣Φ和稀疏基矩陣Ψ的非相關性代替RIP性質判斷觀測矩陣的構建。

其中對于N×M隨機測量矩陣，滿足式(6)可認為滿足RIP性質。

M≥K·log(N)。

(6)

式中K為原始信號稀疏度。

稀疏變換基矩陣Ψ和測量矩陣Φ是否能夠相互表示，可通過式(7)的計算結果大小判定。

(7)

式中：φk為測量矩陣Φ的第k行行向量；ψj為正交矩陣Ψ的第j列列向量。

式(7)表達了矩陣Ψ和矩陣Φ的關聯性，算得的u值越小，表明矩陣Ψ和矩陣Φ兩者越不相關，所得投影后測量值的有效信息越多，重構誤差越低。一般地，無論稀疏基矩陣怎么變化，隨機矩陣與任意一個確定的矩陣都具有較大的不相關性，因此，隨機測量矩陣被廣泛地運用于壓縮感知，常見的隨機測量矩陣主要有隨機高斯測量矩陣和隨機伯努利測量矩陣等。

1.1.3 信號的重構算法

θ矩陣在滿足RIP準則的前提下，通過求解式(2)可以得到稀疏系數，將N維原始信號x從M維投影測量值y中重構出，只需要求解以下欠定問題的最優稀疏解來得出。

(8)

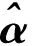
求解式(8)是一個線性規劃求解凸優化問題的過程，L1范數最小化優化求解成為基追蹤算法，本文傳統壓縮感知將采用常用的梯度投影法和內點法進行信號重構。傳統的信號重構算法還有貪婪算法和貝葉斯框架算法。

1.2 結構健康監測大數據傳感器網絡

在監測系統數據傳輸層與儲存層中，傳統監測數據的重構將單個傳感器節點重構，但因為結構監測測區內涉及多個測點，依據測點間的顯著相關性與相似發展趨勢布設相應傳感器網絡，如圖1所示。

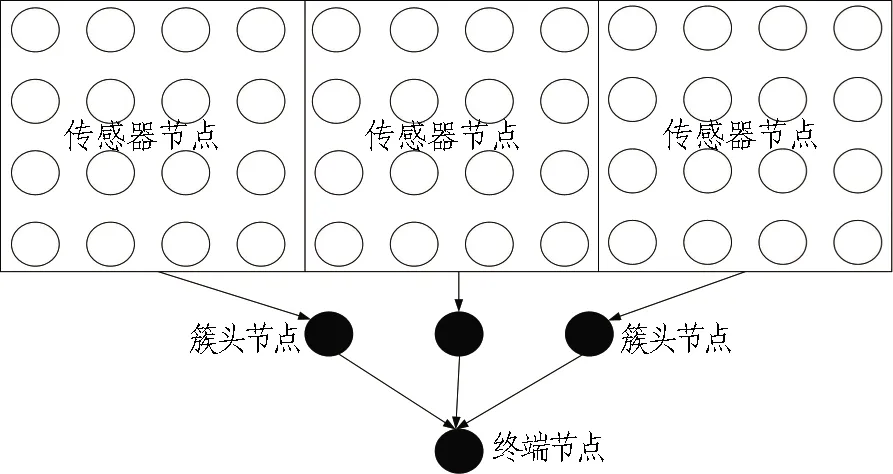
圖1 無線傳感器網絡傳輸示意圖

在運營隧道大型結構中，無線傳感器網絡分布在每個測區的傳感器節點數較多，每個遠程傳感器具備獨立采集、計算、傳輸通信能力。傳感器網絡類屬于全分布式節點網絡，每個傳感器節點監測數據具有偶然性。對于大規模復雜問題，為了獲得監測區段最接近實際的監測數據，以期分析出精準的健康狀態結果，需要最大程度地發揮傳感器節點之間的協同能力。運營隧道健康監測系統中需要改變傳統單一的數據傳輸方式，采用簇頭節點到終端的傳輸，簇頭的選擇對應了每個測區的傳感器網絡。

進行運營隧道結構健康監測時，無線傳感器網絡中部分傳感器的采集頻率大，1 d內單傳感器監測的數據達百萬級，加上測區均勻分布有多個傳感器，兩兩之間的監測數據存在冗余，而基于傳感器網絡的壓縮重構可以解決數據采集量極大、傳輸壓力大的問題。通過壓縮采集對測區傳感器網絡協同融合，將融合數據進行測量編碼轉入簇頭節點傳輸到終端，在終端實現監測數據的重構。

綜上所述，建立了基于傳感器網絡的壓縮感知重構算法的理論框架。一般來說，傳感器網絡每個測區的傳感器具有獨立稀疏性，傳統做法對每個監測信號進行稀疏變換，將稀疏變換系數傳輸到簇頭節點進行編碼測量，最終傳輸到終端設備。本文基于信號的獨立性和相關性建立網絡式的稀疏變換，對稀疏網絡進行編碼測量，解決單個傳感器節點的數據冗余以及處理次數的問題。

1.3 面向大數據的基于傳感器網絡的壓縮感知重構算法

1.3.1 傳感器網絡聯合稀疏表示

傳感器網絡聯合稀疏表示即將所有的傳感器節點監測數據整合進行稀疏變換。假設運營隧道相鄰斷面有K個傳感器節點，每個傳感器節點在相同時間點tj同時采集1次數據，其中j=1,2,…,N，采樣時段為[0,t]，采樣頻率T=N/t,原始采集的信號矩陣N×K用U表示，如式(9)所示。

(9)

式中UNK為第K個傳感器節點N的監測數據值。

相較于傳統監測采集技術，壓縮感知無須遵循Nyquist定理，實際采集的信號為殘缺矩陣。假設有集合Ω={(N,k)}以及置零矩陣PΩ：RN×k→RN×k，則有：

Y=PΩU。

(10)

(11)

一般的監測信號在頻域上呈現稀疏性，信號重構從測量信號Y中重構出原始矩陣U，可表示為

U=Ψ·u。

(12)

式中：Ψ為離散傅里葉矩陣；u為單節點測量矩陣。

為表現基于傳感器網絡的壓縮感知重構算法的優勢，體現算法的群稀疏性，求解X∈R時采用最小化范數的形式書寫，采用Tikhonov法解決正則化問題，即式(12)可變換為

(13)

式中：μ為正則化參數；Z為正則化約束。

1.3.2 采用Split Bregman求解凸優化問題

Split Bregman迭代算法類屬于圖像恢復前沿科學的算法，對大型多維數據的重構具有迭代速度快、重構精度高的優勢，具體的求解原理如下。

以下定義Bregman距離。假設泛函J在u點的子梯度為J(u)且u∈X(X→R)，p點是其對偶空間中的某一點，即對于u，v∈X(X→R)和p∈?J(u)，則Bregman距離定義如式(14)所示。

(14)

基于Bregman距離，將式(14)轉化為無約束的優化問題，如式(15)所示。

(15)

式中φ(u)、H(u)為凸函數且在u處可微。

令d=φ(u)，代入Bregman距離，可以得到

(16)

式中λ為控制參數。

依據Bregman迭代算法和Bregman距離，可以得到

(17)

(18)

(19)

將式(17)—(19)展開，可得到

(20)

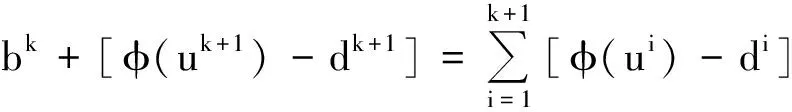
(21)

1.3.3 凸優化求解的迭代過程

本文引入凸優化理念，通過迭代方法求解式(13)。

1)初始條件：k=0，u0=0，b0=0；2)選擇合適的收斂參數τ；3)按以下過程進行迭代求解，即通過Split Bregman迭代公式可以得到。

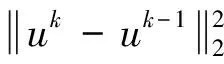
(22)

基于傳感器網絡的壓縮感知重構算法采用迭代法尋找最優解，能夠在一定程度上保證算法的收斂。與此同時，基于傳感器網絡的壓縮感知重構算法原理將同一測區相鄰多個測點傳感器網絡數據稀疏化集合進行重構，充分利用了監測信號的相關性特征。

2 基于大數據傳感器網絡的壓縮感知重構算法實例分析

2.1 工程概況

湖北省武漢市地鐵3號線于2015年12月28日正式運營，其中王宗區間右線里程起點DK9+996.728，向宗關方向大概延伸300 m，區間經過王家灣中心商業區和購物休閑廣場。區間隧道為2條外徑為6.2 m的左右雙線隧道，隧道左右線間距為13～18 m，盾構隧道埋深14～41 m。根據地質勘探資料，隧道所在區間土質分布情況從上到下依次為雜填土、黏土、粉質黏土、粉土、粉質黏土、粉砂互層、粉細砂，運營隧道賦存土層段為粉砂互層與粉細砂層之間。

監測點與傳感器網絡布設圖如圖2所示。在運營隧道結構健康監測系統中，本監測項目實際采用6個加速度傳感器監測隧道6個斷面，分別命名為1—6號傳感器，傳感器采集頻率為50 Hz，單次采集時間為30 min。

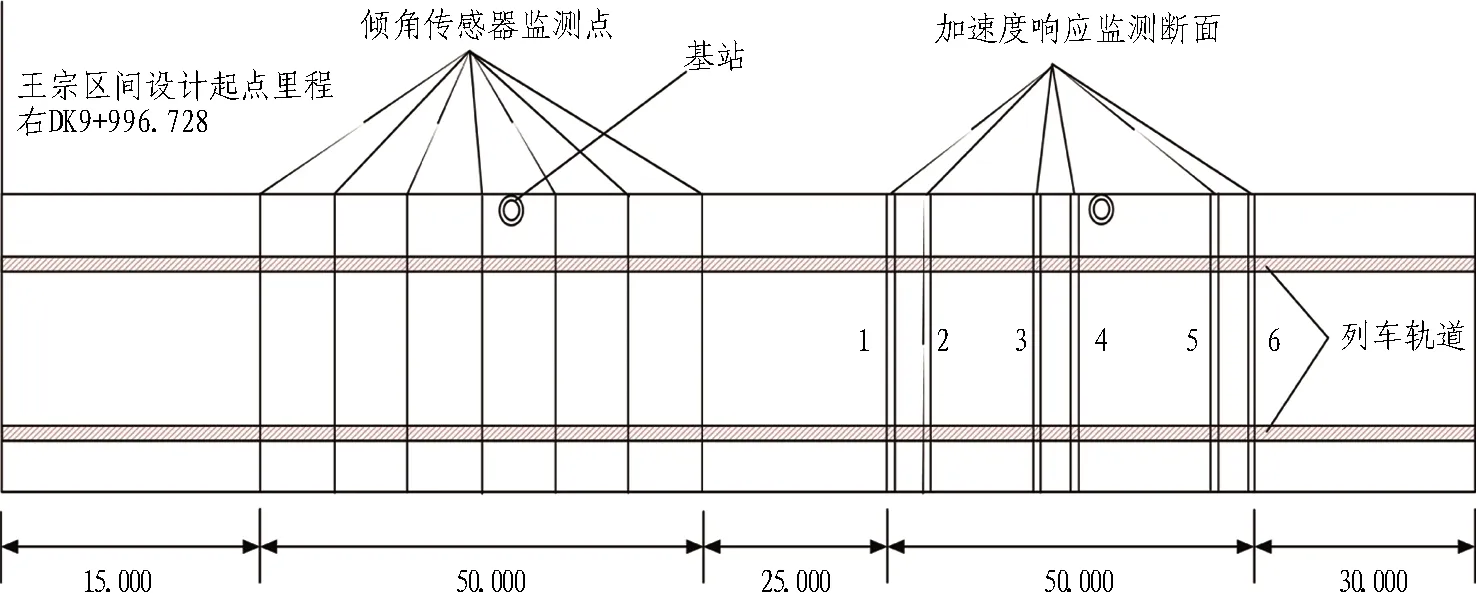
圖2 監測點與傳感器網絡布設圖(單位：m)

2.2 信號壓縮采樣及重構

為保證數據的相關性且具備一定量試驗組的要求，選取1個測試區6組傳感器(1—6號傳感器)數據作為研究對象，取每單次監測的10 000個檢測序列進行研究。圖3示出1—6號加速度傳感器信號時程圖，可以看出6個加速度傳感器測得的數據都較為平穩，幅值波動較為近似，相關性較大。

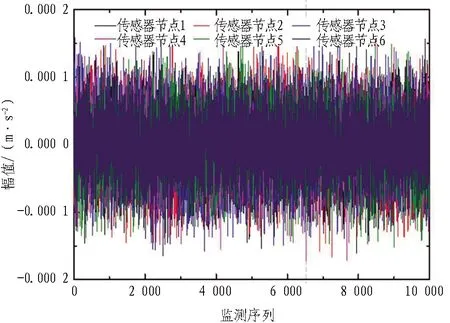
圖3 1—6號加速度傳感器信號時程圖

基于傳感器網絡的壓縮感知重構算法針對相同測區傳感器網絡在相鄰測點的傳感器節點監測信號在頻域幅值有稀疏相關性，通過對原始信號矩陣進行傅里葉變換提取頻域信號。1—6號加速度傳感器信號傅里葉變換圖如圖4所示。可以看出6個傳感器節點在頻域幅值呈現高稀疏相關，信號重構效果更加精準。為更直觀地反映傳感器網絡的相關性，用 Pearson 相關系數來表達監測信號之間的相關性，計算公式如式(23)所示。

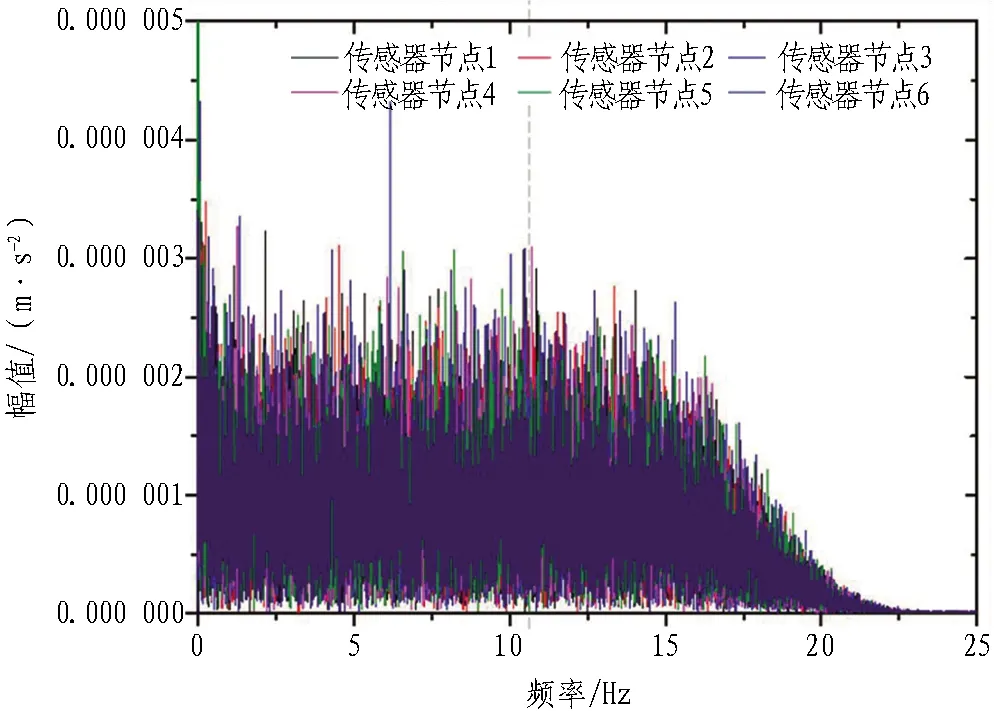
圖4 1—6號加速度傳感器信號傅里葉變換圖

(23)

式中：A、B為監測數據；i為傳感器節點號；C為相關系數。

通過計算傳感器網絡6個傳感器節點監測信號兩兩之間的相關系數，得出監測信號之間在頻域的相關系數C集中在0.732～0.891，原始信號矩陣各傳感器節點之間有強稀疏相關，滿足群稀疏化的特征，傳感器網絡算法重構結果更加精確。

本節對采集的加速度響應信號進行傳統單節點壓縮感知重構算法和基于傳感器網絡的壓縮感知重構算法處理，取傳感器節點1不同采樣率數據時域幅值重構結果和誤差，如圖5—11所示。

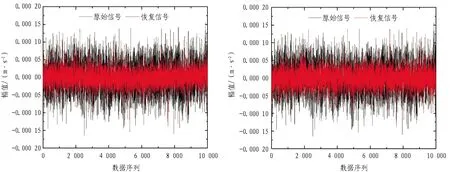
(a)傳統單節點壓縮感知重構算法 (b)基于傳感器網絡的壓縮感知重構算法

(a)傳統單節點壓縮感知重構算法 (b)基于傳感器網絡的壓縮感知重構算法

由圖5—11可以發現：對于傳統單節點壓縮感知重構算法和基于傳感器網絡的壓縮感知重構算法，數據采樣率越大，數據重構精度越高；相同采樣率條件下，基于傳感器網絡的壓縮感知重構算法的重構精度要大于傳統單節點壓縮感知重構算法。

2.3 信號重構誤差分析與健康監測應用驗證

2.3.1 誤差分析

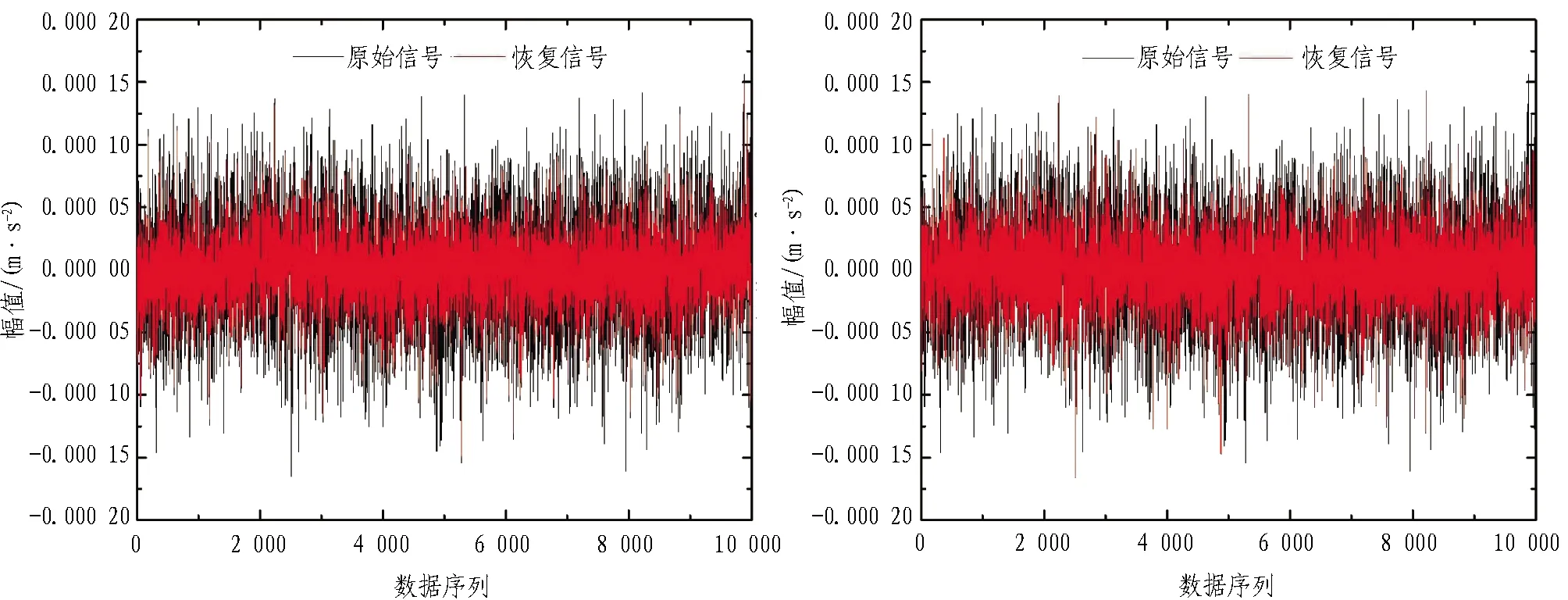
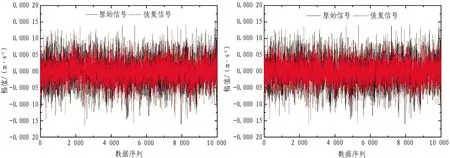
壓縮感知數據的壓縮采集到恢復重構針對不同數據特征類型有相應的適用性和精準性。由圖5—11可知，基于傳感器網絡的壓縮感知重構算法總體比傳統單節點壓縮感知重構算法重構精度高。相較于圖11信號均方根誤差，為更直觀地獲得傳感器網絡矩陣誤差，以分析2種重構算法在采樣率因素下的重構精度，引入范數誤差，如式(24)所示。

(24)

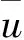
(a)傳統單節點壓縮感知重構算法 (b)基于傳感器網絡的壓縮感知重構算法

(a)傳統單節點壓縮感知重構算法 (b)基于傳感器網絡的壓縮感知重構算法

(a)傳統單節點壓縮感知重構算法 (b)基于傳感器網絡的壓縮感知重構算法

(a)傳統單節點壓縮感知重構算法 (b)基于傳感器網絡的壓縮感知重構算法

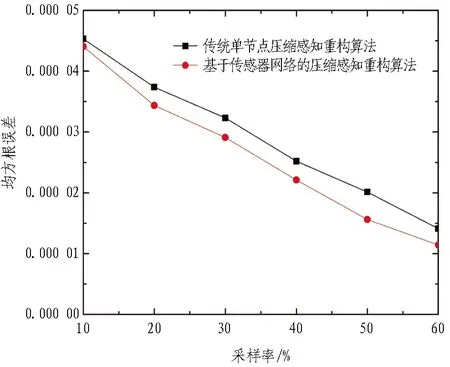
圖11 傳統單節點和基于傳感器網絡的壓縮感知重構算法時域幅值重構結果均方根誤差

表1為傳統單節點和基于傳感器網絡的壓縮感知重構算法在時域幅值的重構誤差。可以看出：由于監測信號類型、特征與結構性因素，每個傳感器節點在時域幅值上的重構精度不一。隨著采樣率增加，監測信號重構精度增加。相同采樣率條件下，基于傳感器網絡的壓縮感知重構算法的重構精度更高，表明基于傳感器網絡的壓縮感知重構算法可以有效增加信號重構精度。在實際運用中，選取更大的采樣率可以恢復到更精確的重構信號。

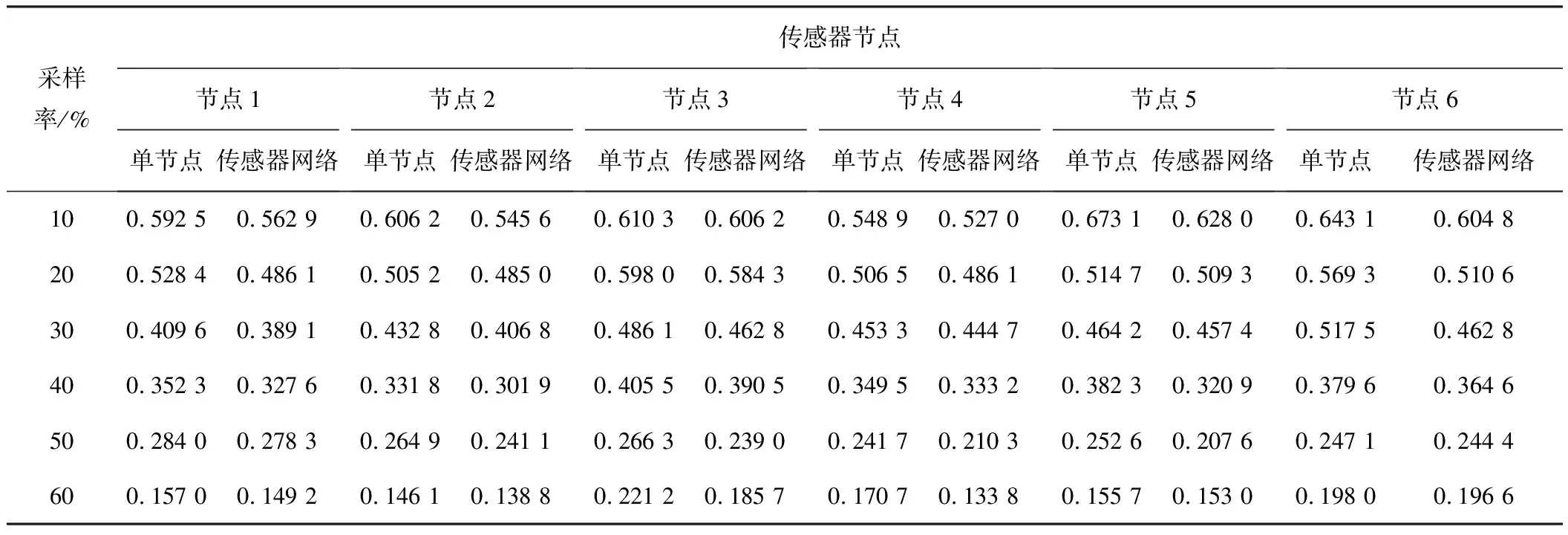
表1 傳統單節點和基于傳感器網絡的壓縮感知重構算法在時域幅值的重構誤差

2.3.2 運營隧道結構健康監測系統應用驗證

在實際運營隧道健康監測中，一般采用加速度頻譜數據進行隧道健康評價，因此需要對原始信號和重構信號進行傅里葉變換，轉換為頻域數據后再對比重構誤差。表2為傳統單節點和基于傳感器網絡的壓縮感知重構算法在頻域幅值的重構誤差。

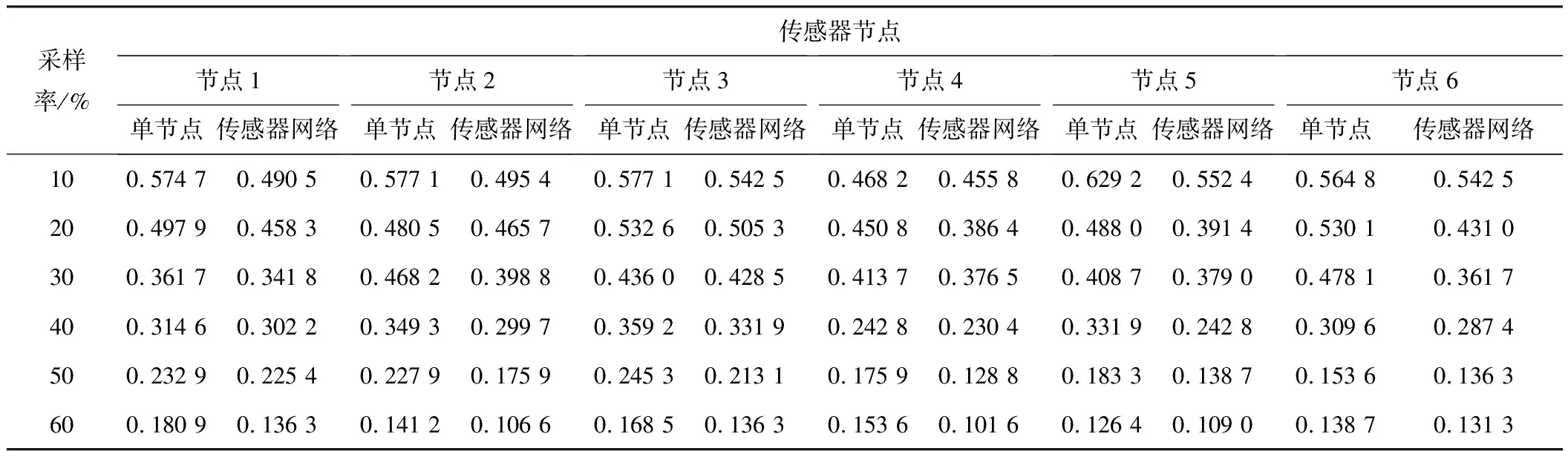
表2 傳統單節點和基于傳感器網絡的壓縮感知重構算法在頻域幅值的重構誤差

由表2可以看出：對于加速度信號時域幅值規律性弱、頻域幅值規律性強的信號，其頻域幅值的重構誤差更小；相同采樣率條件下，基于傳感器網絡的壓縮感知重構算法的重構精度比傳統單節點壓縮感知重構算法高；隨著采樣率增加，2種方法的重構精度提高，基于傳感器網絡的壓縮感知重構算法精度提升更為顯著。

本監測項目監測的加速度信號有盲稀疏度、高噪聲干擾以及結構性弱的特征，在低采樣率下重構的時域幅值誤差偏大，隨著采樣率增加，誤差有所減小。基于傳感器網絡的壓縮感知重構算法依據傳感器數據結構的相似性，重構誤差有所減小。在實際工程應用過程中，要保證監測預警的準確性，采樣率為60%以上，均方根誤差為1.06×10-5，式(24)誤差為0.193，總體誤差在20%以下，達到工程應用標準。

2.3.3 傳感器網絡節點數量耦合效應研究

為了研究傳感器網絡中節點數量對于信號壓縮重構的影響，將斷面加速度傳感器的數量增加到了10個，并對不同采樣率和傳感器節點數量下的重構精度進行了計算。圖12示出采樣率為10%～60%、傳感器網絡節點為1～10個的時域幅值重構誤差。可以看出，基于傳感器網絡的壓縮感知重構算法中傳感器的個數及監測斷面、斷面布設傳感器的數量對重構誤差也有影響，傳感器網絡矩陣中傳感器節點數對最終信號重構時(頻)域幅值的誤差有不同程度的影響。

由圖12可以看出：隨著監測信號采樣率增加，加速度響應在時域幅值的重構誤差下降，恢復信號精度增加；隨著傳感器網絡節點數的增加，相同采樣率條件下，整體的恢復信號重構誤差均有不同程度的下降；當傳感器節點增加至6個以后，曲線趨于收斂，重構誤差不再有明顯下降，表明在基于傳感器網絡的壓縮感知重構算法中，針對不同類型、特征、結構性監測信號，存在一個耦合上限。本研究的加速度傳感器的監測耦合上限為6個，超過這個數值后，重構精度沒有明顯變化。

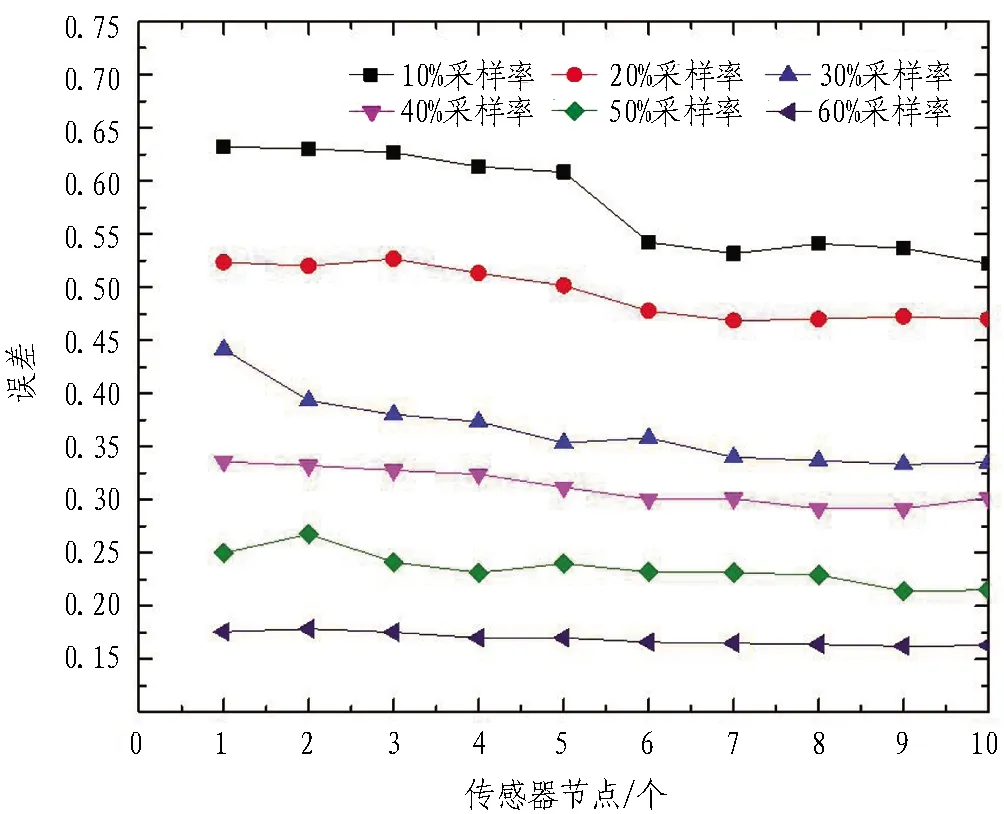
圖12 時域幅值重構誤差和傳感器節點數量的關系

3 結論與討論

1)本文基于傳統單節點壓縮感知重構算法，引入傳感器網絡框架表示模型，建立基于傳感器網絡的壓縮感知重構算法，采用迭代方法求解最小化范數問題，具有很好的收斂性，可以得到比傳統單節點壓縮感知重構算法更精確的重構結果，壓縮采樣率為60%以上，總體誤差在20%以下，符合工程應用標準。

2)針對不同類型、特征、結構性監測信號，基于傳感器網絡的壓縮感知重構算法存在一個耦合上限。本文研究的加速度傳感器的監測耦合上限為6個，超過這個數值后，重構精度沒有明顯變化。

3)本文只針對一種信號類型進行了試驗，如果利用耦合性壓縮算法對不同信號類型進行壓縮重構可能會無差別過濾異常信號，導致不能正常反映隧道健康關鍵信息。下一步研究需要采取不同的壓縮重構算法處理不同的信號類型，以實現多種信號的耦合壓縮感知。