超孔隙水壓力對盾構隧道極限支護力影響研究

陳相宇, 潘 茜, 丁建軍

(佛山軌道交通設計研究院有限公司, 廣東 佛山 528000)

0 引言

城市過江隧道修建過程中，不可避免需要穿越江河兩岸淺覆土的漫灘區段，而漫灘段往往分布著較厚的富水砂層。富水砂層工程特性復雜，盾構在該類地層中施工時，易發生開挖面土體失穩，甚至地表塌陷情況[1]。富水砂層中盾構施工對孔隙水壓力產生擾動，改變了影響區內土體的應力應變狀態及滲流狀態，進而對盾構隧道開挖面穩定性產生影響[2]。研究盾構施工引起地層孔隙水壓力反應的方法主要包括現場監測、理論計算、有限元模擬等。

在現場測試數據的總結分析方面，Broere[3]對Heinenoord隧道盾構掘進過程引起的地層孔隙水壓力變化進行監測，分析總結了孔隙水壓力隨盾構掘進開挖的變化規律；易宏偉等[4]對軟土地層中盾構施工期間孔隙水壓力反應規律進行了研究總結。

基于Mohr-Coulomb屈服準則，肖立等[5]推導了考慮土體內摩擦角φ時盾構掘進引起的超孔隙水壓力計算公式；魏新江等[6]通過應力釋放理論，推導了隧道襯砌周圍土體的初始超孔隙水壓力計算公式；王志良等[7]基于Mindlin解和Henkel公式推導了盾構掘進開挖面前方超孔隙水壓力的分布特征；丁智等[8]采用數值積分的方法推導了軟土區盾構掘進引起的超孔隙水壓力計算公式。

隨著計算機技術的進步，有限元法也廣泛應用于孔隙水壓力的分析與研究。文獻[9-11]通過數值分析，對滲流場應力場耦合效應及開挖面穩定性進行了研究。國內外相關學者探索研究了極限平衡法在砂性土開挖面極限支護壓力計算方面的應用，總結了修正楔形體模型極限支護壓力公式[12-14]。

目前研究成果多側重于對孔隙水壓力變化規律的總結以及超孔隙水壓力的計算方法研究，或在未考慮超孔隙水壓力的影響下，對盾構開挖面極限支護力進行計算分析，尤其在富水砂層孔隙水壓力反應研究中，考慮超孔隙水壓力對開挖面極限支護力影響的研究成果較少。本文基于某越江公路隧道工程，對盾構掘進前方地層進行孔隙水壓力現場測試，通過實測數據，分析總結盾構施工期間地層孔隙水壓力的空間分布特征以及盾構施工引起的孔隙水壓力變化規律。基于變分學方法，將極限支護力的求解轉化為考慮多維約束的函數極值問題，進而研究超孔隙水壓力對盾構隧道極限支護力的影響，提出修正的極限支護力計算公式，并對盾構泥水艙壓力的設置提出建議，以指導實際施工。

1 工程概況

本文依托的工程，包括2條并行的越江隧道，單條隧道長度約1.6 km，采用泥水平衡式盾構，盾構開挖直徑11.65 m。盾構從東岸始發井開始掘進，穿越江底后到達西岸接收井。盾構隧道在江底段主要穿越強風化礫巖、中風化礫巖層；靠近盾構接收井的河西岸漫灘段，隧道上半斷面及上覆地層分布著較厚的富水粉細砂層，局部存在卵石、圓礫。本文研究對象為河西漫灘段的粉細砂層，本工程地質勘察資料揭示，該處粉細砂層呈褐黃色，濕-飽和，稍密-中密狀，透水性強，如圖1所示。

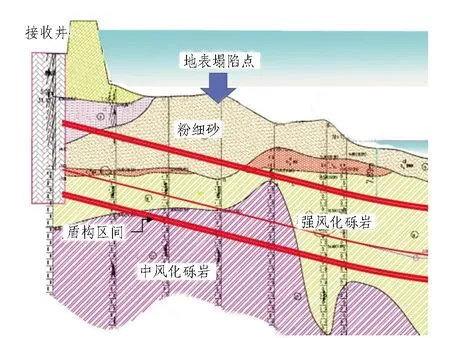
圖1 隧道地質縱剖面

先行線隧道掘進至河漫灘地層時，盾構開挖面前方約1倍洞徑范圍地表出現較大的沉降，局部區域出現地表塌陷，見圖2。

圖2 河漫灘地表塌陷

2 孔隙水壓力測試數據分析

為探明盾構掘進前方富水砂層孔隙水壓力波動及分布情況，在后行線掘進至河漫灘地層時，進行了孔隙水壓力現場測試試驗。

2.1 孔隙水壓力測試方案

在孔隙水壓力測試區段，盾構主要穿越粉細砂層，隧道埋深較淺，覆土厚度約為0.6倍開挖直徑。測試方案中，沿隧道縱向等間距布置5個垂直于隧道軸線的孔隙水壓力測試斷面，編號為Section 1—Section 5，相鄰測試斷面間距d=D/2。每個測試斷面在隧道頂部土體中M1、M2點埋設2個孔隙水壓力計，與隧道拱頂豎向距離分別為1.0、3.0 m。重點測試斷面Section 3，在隧道橫向水平軸線設5個孔隙水壓力測點N1～N5，相鄰測點間距d=D/2，如圖3所示。

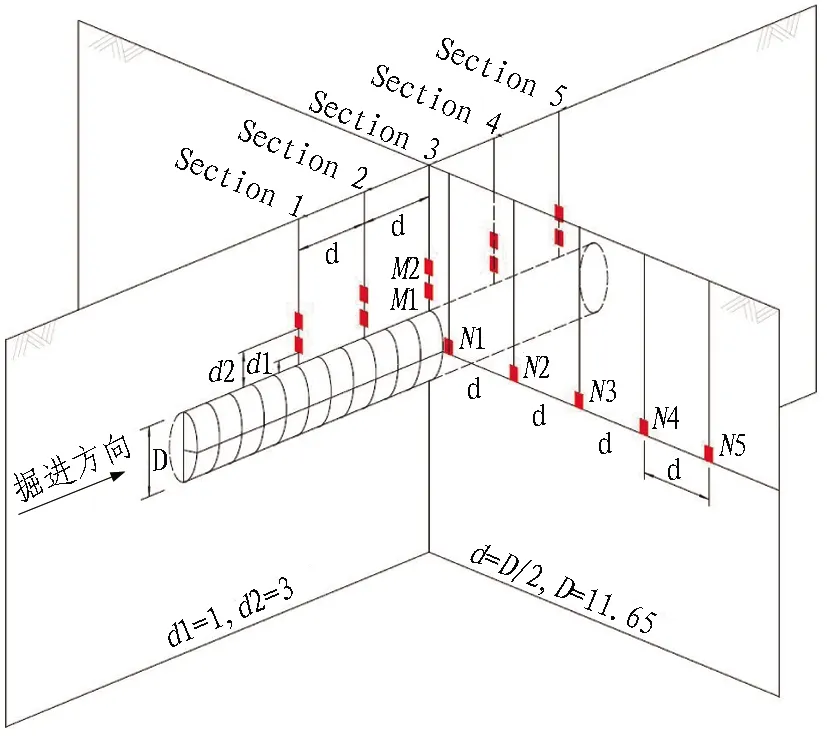
圖3 孔隙水壓力測試方案示意圖(單位: m)

2.2 隧道縱向孔隙水壓力分布

選取Section 2、Section 3斷面的測試數據，分析盾構靠近、通過以及離開測試區的整個施工過程中地層孔隙水壓力的分布及變化規律，變化曲線分別如圖4和圖5所示。

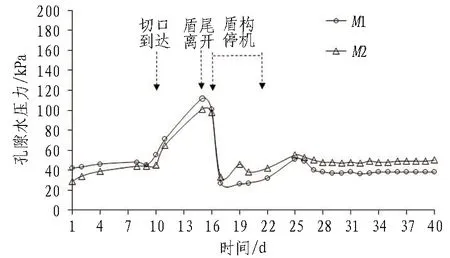
圖4 Section 2孔隙水壓力變化曲線

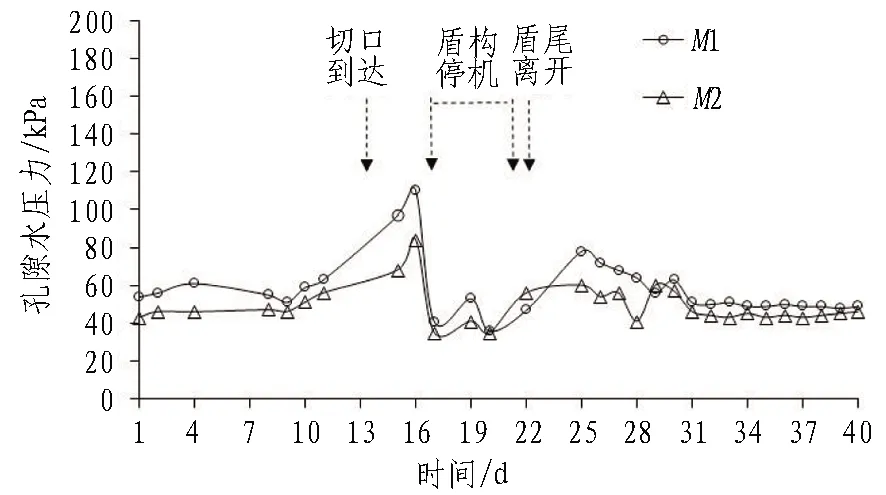
圖5 Section 3孔隙水壓力變化曲線

隨著盾構施工時間的推移及盾構與測試斷面空間關系的變化，盾構施工對地層孔隙水壓力的影響可分為盾構靠近、穿越以及離開測試斷面3個階段。這3個階段包括了盾構與測試斷面的空間關系變化全過程。

測試方案中，Section 3作為重點測試斷面，沿隧道橫向埋設了孔隙水壓力計，故下文以該斷面的孔隙水壓力測試數據為例重點分析。

1)盾構靠近階段。盾構朝著測試斷面Section 3的方向掘進，并逐步靠近孔隙水壓力測點。該階段刀盤在盾構推力作用下，擠壓前方及兩側一定范圍內的土體，致使擠壓影響區域孔隙水壓力增加。

2)盾構穿越階段。盾構到達并穿越重點測試斷面Section 3的過程中，測點孔隙水壓力快速上升，并達到整個過程的孔壓峰值。現場測試數據顯示，該階段M1測點0.110 MPa、M2測點0.084 MPa，可見孔隙水壓力的峰值基本為該階段初始狀態下(盾構剛到達重點測試斷面)的2倍。在測試期第16—22 d(此時盾構刀盤位于Section 4—Section 5)，盾構停機1周，在剛發生停機時，孔隙水壓力迅速消散，下降60%后測值為0.041 MPa。隨后施工單位進行了壁后注漿，壁后注漿期間，測試斷面Section 3的孔隙水壓力值受注漿壓力影響在波動中呈抬升狀態。

3)盾構離開階段。盾構恢復施工并正常掘進至盾尾離開測試斷面Section 3，測點M1的孔隙水壓力也隨即上升，并達到該階段的最大值，測值為0.078 MPa。盾構持續掘進，測點孔隙水壓力逐漸降低。隨著時間的推移，盾構通過后7～8 d，測點孔隙水壓力趨于穩定并維持在盾構到達測試斷面Section 3之前的水平。

通過測試斷面Section 1—Section 5 的超孔隙水壓力計算可知，盾構到達第1個測試斷面Section 1時，該斷面測點處超孔隙水壓力上升到35 kPa；Section 2、Section 3測點也產生了明顯的超孔隙水壓力；距離盾構開挖面較遠的測試斷面Section 5，測點處超孔隙水壓力值小于5 kPa，認為不受明顯影響。超孔隙水壓力沿盾構掘進方向遞減，如圖6所示。

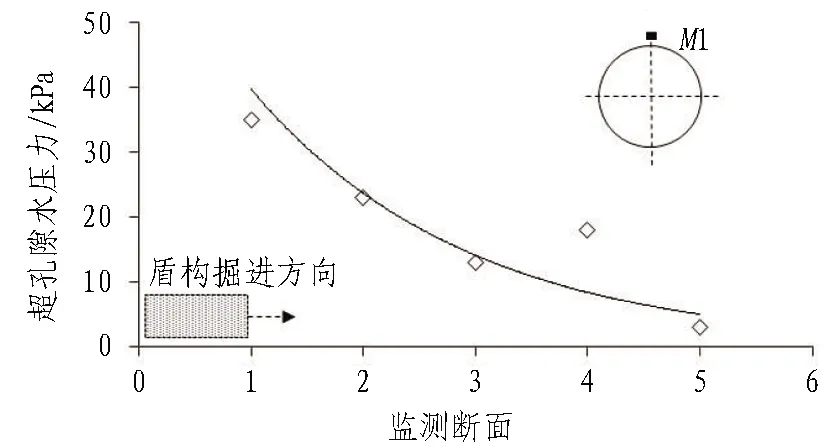
圖6 隧道縱向超孔隙水壓力分布曲線(M1位置處)

沿隧道縱向測點的數據表明，盾構靠近及通過測試斷面期間，周圍土體的孔隙水壓力值明顯上升并達到峰值；盾構通過測試斷面后，孔隙水壓逐漸消散，緩慢回落至初始水平；開挖面前方2倍開挖直徑范圍內為孔隙水壓力擾動區，且隨著與開挖面距離的減小，擾動程度增大。

2.3 隧道橫向孔隙水壓力分布

重點測試斷面Section 3的橫向單側孔隙水壓力測試曲線如圖7所示。Section 3沿隧道橫向共設5個測點，其中測點N3和N4因現場鉆孔條件有限，未能達到設計孔深，測點位于隧道軸線水平面上方6.0、4.0 m。

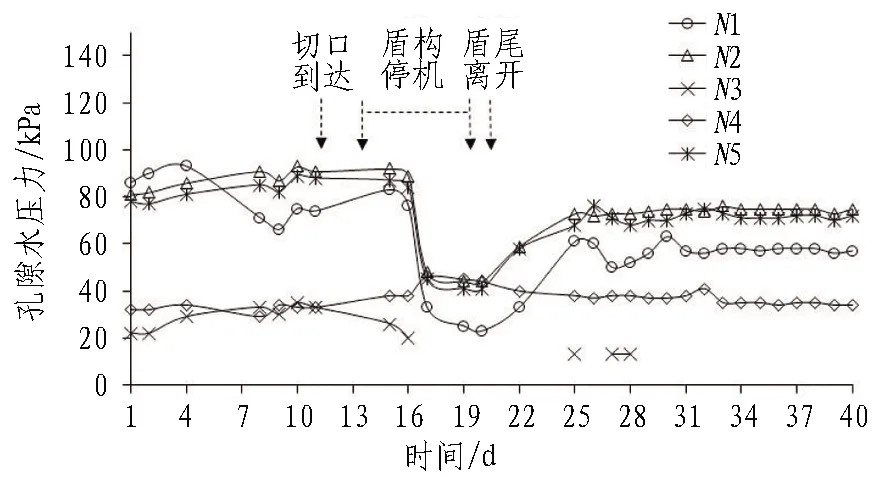
(a)孔隙水壓力變化曲線

根據沿隧道橫向布置測點的數據可知，盾構穿越測試斷面階段，測點N1的孔隙水壓力由0.074 MPa增大至0.080 MPa，產生的超孔隙水壓力為6.0 kPa；測點N2孔隙水壓力從0.088 MPa增大至0.092 MPa，在此過程中產生了4.0 kPa的超孔隙水壓力；隧道橫向1.5倍開挖直徑距離的測點N4產生的超孔隙水壓力較小，不到3.0 kPa；測點N5孔隙水壓變化接近零值，認為幾乎未受盾構施工影響。

盾構切口臨近重點監測斷面Section 3時，沿隧道橫向測點數據及擬合結果表明：盾構施工時，將在開挖面兩側1.5倍開挖直徑范圍內地層中產生較明顯的孔隙水壓力擾動，且越靠近開挖面，擾動程度越大。

3 考慮超孔隙水壓力變化的主動破壞極限支護力研究

3.1 主動破壞極限支護力pmin的確定

盾構施工中，如果設置的開挖面支護壓力p小于開挖面發生主動破壞時所受的側向土壓力pmin，則可能會造成開挖面前方土體產生較大擾動，甚至存在塌陷的風險。基于極限平衡法的思想，確定主動破壞極限支護力pmin，并做以下假設。

1)研究對象為平面問題；

2)土體材料服從Mohr-Coulomb破壞準則；

3)開挖面前方地層發生失穩時，失穩土體為楔形體，其破壞面與開挖面上下頂點連接。

開挖面前方地層發生主動破壞時，失穩土體受力計算模型如圖8所示。隧道底部距地表的垂直距離為h，隧道直徑為D，通過開挖面的上頂點和下頂點的破裂面分別為l1,l2；σ1，σ2，τ1，τ2分別為作用在破裂面y1，y2上的法向應力和切向應力，kPa；p為盾構在開挖面上的作用力。

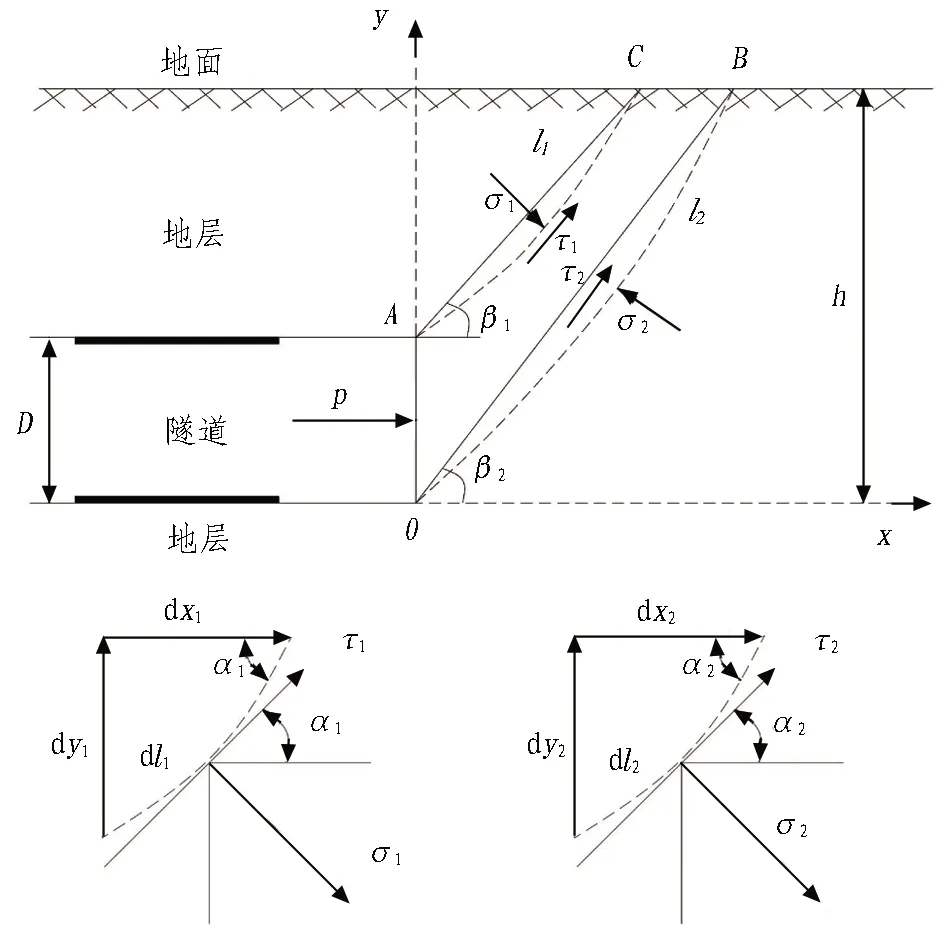
圖8 開挖面前方破裂面受力分析圖

單獨考慮失穩土體AOBC的受力狀態。

由∑x=0和∑y=0可以建立其處于平衡狀態的力的平衡方程

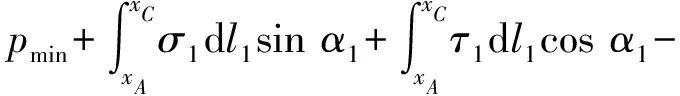
(1)

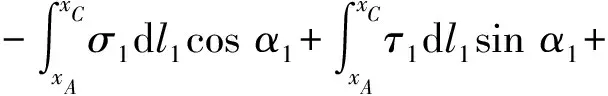
(2)

式(1)—(2)中：xA、xO、xB、xC為滑動塊體頂點A、O、B、C的x向坐標；γs為土體重度，kN/m3；α1、α2、dl1、dl2、dx1、dx2的幾何意義見圖8。從圖8還可得到：

dx1=dl1cosα1;dy1=dl1sinα1。

(3)

dx2=dl2cosα2;dy2=dl2sinα2。

(4)

破裂面上法向應力σ與切向應力τ服從Mohr-Coulomb破壞準則，則對應于破裂面l1,l2

τ1=σ1tanφ+c;τ2=σ2tanφ+c。

(5)

式中c為黏聚力。

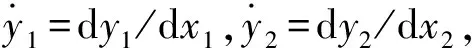
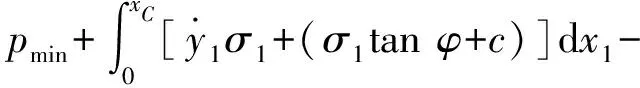
(6)

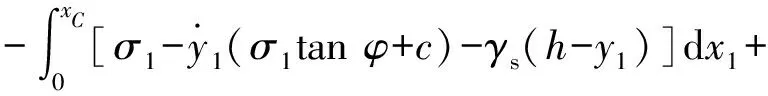
(7)

式(6)和式(7)分別為開挖面前方失穩時土體AOBC的2個受力極限平衡方程。

將破裂面可看作一個待求極值的泛函數，無法直接進行求解，需進行變分變換才能求解極值pmin。依據泛函數在約束條件下的變分法及相關邊界條件，通過Lagrange乘子構造泛函數G，從而將上述的條件極值問題轉化為無約束的極值問題。

(8)

g1=H1+λ1V1，g2=H2+λ2V2。

(9)

(10)

(11)

式(9)中λ1，λ2為Lagrange乘子。由變分學可知，破裂面方程y1(x)，y2(x)及破裂面上法向應力方程σ1(x)，σ2(x)需滿足以下條件。

1)輔助函數H1，H2的Euler微分方程

(12)

(13)

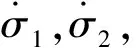
(14)

2)積分約束方程，即式(7)。

3)點B，C處的變分邊界條件

(15)

式中δ為變分算子。

4)邊界點的幾何條件xA=xO=yO=0，yA=D，yC=yB=h。

根據上述邊界幾何條件，可知破裂面方程。破裂面y1(x)，y2(x)及破裂面上法向應力方程σ1(x)，σ2(x)的方程為

(16)

(17)

(18)

(19)

由式(10)和式(11)可知，破裂面方程y1(x)，y2(x)是線性方程，圖8中的破裂面為直線。

破裂面設β1，β2為破裂面與x軸正方向的夾角。即破裂面方程y1(x)，y2(x)可寫為

y1=x1tanβ1+D;

(20)

y2=x2tanβ2。

(21)

對比式(10)和式(11)，可得

λ1=-tan(φ+β1);

(22)

λ2=tan(φ-β2)。

(23)

將式(16)—(23)代入式(6)并化簡，可得到主動破壞極限支護力pmin的目標函數f1。

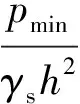
(24)

式中：pmin/γsh2為無量綱化值；f1是破裂角β1，β2的函數。

將式(16)—(23)代入式(7)并化簡，可得到主動破壞極限支護力pmin的目標函數f2。

f2(β1,β2)=0。

(25)

式(24)和式(25)已將待求極值的泛函數轉化為考慮多維約束的函數極值問題。然而，若直接求解式(24)和式(25)，可能帶來計算量過大的問題。Matlab中的fmincon函數可用于計算多維約束非線性函數最大值的求解。利用該函數命令可先求出支護壓力p的最小值(即求解-p的最大值)。其待求解的目標函數為式(24)，設定該函數約束條件如下：

1)β1，β2取值區間為[0,π/2]；

2)滿足非線性公式(25)約束；

3)破裂面上切向應力τ大于0。

3.2 超孔隙水壓力水對極限支護力的影響

富水砂層中開挖面前方土體受到盾構掘進的擾動，土體間產生超孔隙水壓力Δμw(kPa)，土體強度隨之降低[15]。

飽和土體任意截面總應力σ=σ′+μw。σ′為土體有效應力，μw為土體孔隙水壓力。當孔隙水壓力增加Δμw，則此時土體有效應力為(σ′-Δμw)。本文假設Δμw沿盾構隧道前方破裂面呈線性遞減分布，且應力方向與土體有效應力相反，如圖9所示。

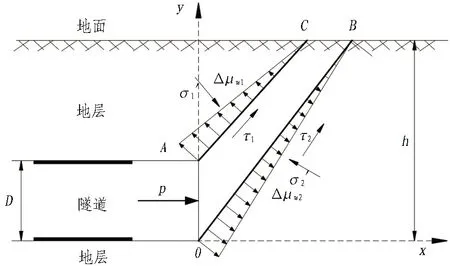
圖9 超孔隙水壓力影響分布圖

假定孔隙水壓力在O點和A點處均為Δw，在B點和C點處均為0；則可知超孔隙水壓力沿破裂面分布的計算式為：

(26)

(27)

式(18)和式(19)在考慮超孔隙水壓力的影響后，可改寫為

(28)

(29)

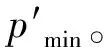
圖10 影響系數隨超孔隙水壓力變化曲線

由圖10可知，超孔隙水壓力波動對開挖面前方極限支護力的設定影響較大。對應上文實測結果，當超孔隙水壓力增加35 kPa時(如Section 1所示)，極限支護力的設定應比正常情況增加約59%；當超孔隙水壓力增加13 kPa(如Section 2所示)時，極限支護力的設定應比正常情況增加約30%。

通過本工程盾構穿越的粉細砂地層取樣及三軸壓縮試驗(固結不排水)，獲得試樣不排水抗剪強度ccu=9.6 kPa，φcu=30.1°。

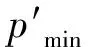
圖11示出當時塌陷區域盾構泥水艙壓力曲線，因現場實際施工中未考慮孔隙水壓力影響，該段掘進中泥水艙壓力設置值偏低，僅為0.12～ 0.14 MPa，小于主動破壞極限支護力的理論計算值。隧道掘進至600環附近時地表出現較大的沉降，隨著盾構持續低泥水壓力掘進，至607環時出現了地表塌陷(見圖2)。

圖11 塌陷區域盾構泥水艙壓力設置曲線

同時，通過黏聚力和內摩擦角對pmin的影響計算可知，黏聚力的存在及內摩擦角的增大，減少了實際需要的作用力大小，因而，在黏聚力和內摩擦角增大時，地層的自穩能力增加，更易保持開挖面的穩定，如圖12所示。

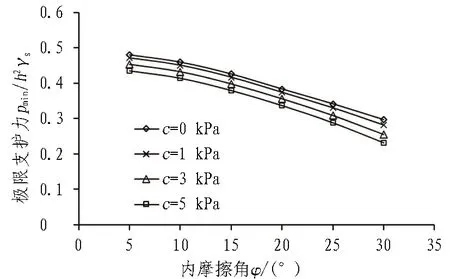
圖12 黏聚力和內摩擦角對pmin 的影響曲線

4 結論與討論

基于盾構施工期間孔隙水壓力反應規律的分析以及超孔隙水壓力對隧道開挖面主動破壞極限支護力影響的研究，得出以下結論：

1)富水粉細砂地層泥水盾構掘進施工時，將在開挖面前方及兩側的地層中產生孔隙水壓力擾動區；該擾動區邊界大致為開挖面前方2倍的開挖直徑、開挖面兩側1.5倍開挖直徑，且越靠近開挖面，擾動程度越大。

2)在考慮超孔隙水壓力對極限支護力影響的工況下，基于極限平衡理論，提出修正的極限支護力計算公式；富水砂層中盾構施工應適當提升泥水艙壓力，或采用全泥水平衡模式保持開挖面穩定，同時提高泥膜質量，保持勻速、較快的掘進速度，減小對孔隙水壓力的擾動范圍及擾動程度。

本文研究超孔隙水壓力水對極限支護力的影響是基于二維的計算分析，未考慮三維作用，同時未計入孔隙水壓力波動的時程影響，后續可結合理論計算、數值模擬對上述2方面開展研究。