碎石樁復合地基承載力研究

王 昂

（天津國土資源和房屋職業學院，天津 300270）

0 引言

碎石樁復合地基是地基處理中常用的方法，對于碎石樁復合地基承載力的計算理論多以平面應變理論為基礎，假定碎石樁復合地基的破壞是一個平面應變問題并考慮置換率的影響，這種假定有其合理性，但精確度較低，因此有必要對其進行進一步深入研究。

隨著計算機技術的不斷發展，為研究碎石樁復合地基提供了有效便捷的工具，通過計算機仿真模擬研究碎石樁復合地基破壞模式成為一種趨勢。國內外學者通過不斷的研究取得了大量的成果，針對碎石樁的承載力性能的研究，目前存在多種理論、方法［1-8］。然而大部分的研究工作是針對碎石樁單樁破壞模式和承載力的研究，未考慮群樁及基礎承臺的影響。 因此對碎石樁復合地基的研究還可以進一步深入。

本文利用計算機仿真模擬研究碎石樁復合地基的破壞特點，以此為基礎，通過理論推導得出碎石樁復合地基承載力計算的理論公式，并對該公式進行適當簡化，結合工程實例進行驗證，得出可用于指導工程實踐的碎石樁復合地基承載力計算公式。

1 碎石樁復合地基破壞曲線研究

針對碎石樁復合地基的破壞模式的研究，主要采用兩種方法：一種方法是我國規范采用的方法，將碎石樁的樁和土分開考慮，分別確定出碎石樁和土的承載力，并考慮置換率，依次得出碎石樁復合地基的承載力；由樁和土的彈性模量和抗剪參數及各自的破壞模式依次來確定復合地基的最終承載力；第二種方法則將碎石樁和土整體考慮，考慮置換率的影響，按照土的破壞模型綜合得出復合地基的最終承載力。然而這兩種方法在實際工程應用中誤差均較大，因此有必要對其進行進一步的研究。

本文以摩爾庫倫準則及太沙基地基承載力理論為基礎，采用第二種方法進行碎石樁復合地基承載力研究。通過研究發現碎石樁復合地基的破壞曲線與拋物線形狀極為相似，通過三個關鍵點M、H、W點確定出碎石樁復合地基破壞曲線的方程如公式（1）所示［9］，其中，W點為隆起土體最外側；M點為承臺下的近似三角形區域的最外側；H點為承臺邊緣處位移等于M點和W點位移的加權平均值。M、H、W點位置如圖 1 所示。

圖1 復合地基破壞曲線計算示意圖

碎石樁復合地基的破壞曲線為：

2 碎石樁復合地基承載力計算公式

2.1 碎石樁單樁復合地基承載力理論公式

根據得到的碎石樁復合地基破壞曲線，對其進行受力分析，由于假定承臺為方形，故可取三維模型的 1/4 進行受力分析（見圖 2），其受力如圖 3 所示。

圖2 四分之一破壞土體示意圖

圖3 破壞土體受力分析圖

其中：G為破壞土體重力，kN；Gu，s為樁周土的抗剪強度，Gu，s=（Cs+σNtanφs），kPa；Cs為樁周土的黏聚力，kPa；φs為摩擦角，°；Cu，m為復合土體的抗剪強度，Cu，m=（Cm+ptanφm），kPa；Cm、φm為復合土體的黏聚力和摩擦角，單位分別為 kPa 和°，cm=mcp+（1-m）cs；σN為樁周土的支持力，kPa；p為由主動區傳來的壓力值，kPa。

設關鍵三點的坐標值分別為M（0，d）、H（D/2，h）、W（w，0），根據破壞土體的受力平衡可推導出主動區傳來的壓力值p值計算如式（2）所示。

式中：α為Cu，s在滑動面上的合力為Fc水平面夾角，

結合承臺下1/4棱錐體受力分析，最終可得出碎石樁復合地基承載力計算公式如公式（3）所示。

式中：γm為復合土體的重度，γm=mγp+（1-m）γs，kN/m3。

2.2 碎石樁單樁復合地基極限承載力計算公式的簡化

由于理論公式過于繁瑣，應用不便，有必要對其進行簡化。為簡化該計算公式，做出以下假定。

1）M、H、W三點位置不變，將三點間的拋物線簡化為直線；

2）將復合地基的破壞區域分為為主動區（Ⅰ 區）、推移區（Ⅱ 區）、破壞區（Ⅲ 區），如圖 4（a）所示。

3）假設Ⅰ區與 Ⅱ 區之間的相互作用力只有接觸面間的法向接觸力，而沒有切向接觸力，Ⅱ區傳遞到Ⅲ區的只有水平力；

4）假定 Ⅲ 區外表面所受的力為均布力，其大小與 h/2 深度處外表面上的點受力相同。

對簡化后的模型進行受力分析，如圖 4 所示。

圖4 破壞面受力分析

由此出碎石樁單樁復合地基承載力計算公式如公式（4）所示：

由于推導時做了簡化，為保證公式的準確度，將σru乘以誤差修正系數K。由此得到碎石樁單樁復合地基承載力計算公式如公式（5）所示：

各參數計算值與模擬值之間的對比如圖 5 所示。從圖中可看出，計算值與模擬值誤差較小。

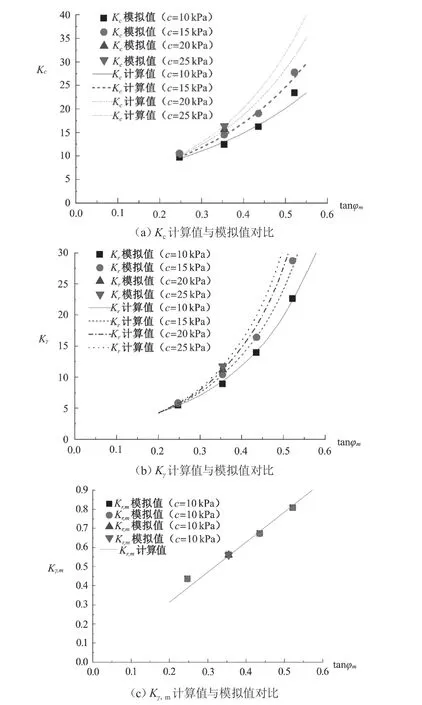
圖5 各參數對比情況

考慮承臺寬度影響，引入承臺寬度影響系數KD=0.1D+0.9。不同承臺寬度下碎石樁單樁復合地基模擬值與計算值的對比情況如圖 6 所示。

圖6 承臺寬度影響系數對比

由此得出簡化后碎石樁復合地基單樁承載力計算公式如公式（7）所示：

2.3 碎石樁群樁復合地基極限承載力計算公式

在群樁作用下，角樁、邊樁及中心樁所受的應力與單樁時有很大差別，經過研究發現這種差別與承臺寬度、樁與承臺中心距有關。為考慮群樁效應的影響，引入群樁效應系數Kq，以此考慮群樁影響。

當承臺長寬比≥3 時，碎石樁復合地基承載力計算按平面問題計算可獲得較高精度，因此，本文只考慮承臺長寬比＜3的情況。經過數值模擬發現，當承臺長寬比＜3時，土體破壞形狀仍然近似于圓錐體（見圖 7），此時將承臺按照面積相等的原則看作正方形承臺對最終結果影響較小，承臺的等效寬度D=L1、L2，L1、L2分別為承臺的長度及寬度。

圖7 矩形承臺復合地基位移云圖

式中：l為碎石樁到承臺中心的平均距離，m；n為非中心樁個數，個；li為碎石樁樁與承臺中心距離，m。由此得出碎石樁群樁復合地基的承載力計算公式如公式（8）所示。

3 公式的實例驗證

由于本研究內容偏重理論研究，在研究過程中由于多種原因未能進行原位試驗。為檢驗本研究成果的正確性，需選取具有代表性的原位試驗進行驗證。陳建峰等進行的碎石樁復合地基現場原位測試試驗［10］中碎石樁復合地基的施工方法為我國普遍采用的施工方法，能夠代表碎石樁復合地基的工程實例，具有普遍性，原位測試的步驟符合我國同行做法，并且該測試針對碎石樁群樁復合地基進行，因此可以很好地檢驗本文公式的普適性。

3.1 工程地質概況

現場土共 2 層，上層為粉質黏土，厚度h=1m，c=2 kPa，φ=35°，γ=13.9 kN·m-3；下層為黏土，h=13 m，c=2 kPa，φ=24°，γ=13.9 kN·m-3。

碎石樁材料參數為：樁長 5.1 m，樁徑 0.76 m，c=4 kPa，φ=47°，γ=19.8 kN·m-3。

現場試驗采用四樁承臺，承臺尺寸為 2.288×2.288 m，碎石樁間距 1.068 m，承臺厚 0.46 m。

3.2 現場原位試驗結果

現場原位試驗得到碎石樁群樁復合地基的荷載-位移曲線如圖 8 所示，根據我國規范可得，該復合地基極限承載力為 275.6 kPa。

圖8 碎石樁原位試驗 p-s 曲線

3.3 本文公式計算結果

按照本文公式（7）進行計算，最終得出該碎石樁群樁復合地基的極限承載力為 256.7 kPa，與實際試驗結果 275.6 kPa 相差 6.9 %，精度較高。

4 結論與展望

本文根據數值模擬結果進行理論推導并適當簡化后，考慮承臺尺寸、群樁效應等影響因素，得出非平面應變條件下碎石樁復合地基承載力計算公式。經過與現場試驗對比分析發現，該公式有著較廣泛的適用性和較高的精度，能夠為類似工程案例提供指導作用。

然而，本文并未考慮地下水的影響，因此可以針對地下水的影響進行進一步的研究；本文對碎石樁復合地基極限承載力的研究中沒有考慮墊層對其極限承載力的影響，因此，后繼工作可針對這一情況做進一步的研究。Q