非交換無色散 Gelfand-Dickey 方程族的附加對稱

胡美艷,李傳忠

（寧波大學 數(shù)學與統(tǒng)計學院,浙江 寧波 315211）

無色散可積系統(tǒng)(KP、Toda 等)是低維可積場中的重要系統(tǒng),主要應用于數(shù)學、物理、拓撲場、矩陣模型等領域[1-2].無色散可積系統(tǒng)的構造是將經典可積系統(tǒng)中的算子和李括號替換為相位函數(shù)和泊松括號,可以看成是經典可積系統(tǒng)的一種形變或類似.類似經典的可積系統(tǒng),無色散可積系統(tǒng)具有許多優(yōu)良的性質,如Lax 對、無窮守恒量和對稱性[3-4]等.近年來,附加流顯式形式的附加對稱性[5-7]引起了廣泛關注.20 世紀80 年代,Orlov 等[5]給出了構造無窮多可積非線性演化方程附加對稱性的一般方法.20 世紀90 年代,Leur[8]研究了KdV型方程族的弦方程和W1+∞約束,Takasaki 等[1-4]研究了無色散的可積方程族(KP、Toda).21 世紀以來,Wang[9]和Li[7]分別對非交換KP 和GD 方程族的附加對稱做了研究,Wang 等[10]也研究了無色散非交換KP 方程族的多哈密頓結構.本文利用類似的方法研究非交換無色散GD 方程族的附加對稱.

1 預備知識

在非交換可積系統(tǒng)的研究中,瑪雅代數(shù)[11-13]發(fā)揮著極其重要的作用,其中瑪雅乘積?的定義為:

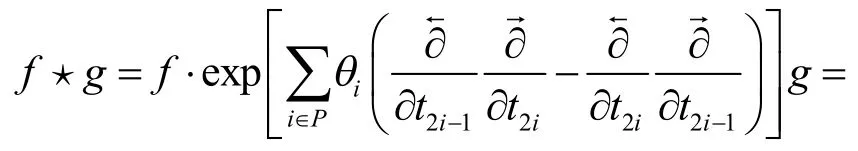
式中:P表示一組有限整數(shù);t2i-1,t2i(i∈P)是非交換坐標;θi表示非交換參數(shù);?(θ2)表示高階項.當θi→0時,非交換系統(tǒng)將被簡化為交換系統(tǒng).

非交換無色散GD方程族的Lax函數(shù)L 定義為:

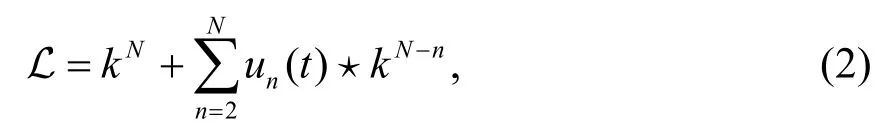
其中u=u(x,t1,t2,…).非交換無色散GD 方程族的Lax 方程為:

N=2時,L=k2+u2是非交換無色散KdV方程族的Lax 函數(shù),其中包含非交換無色散KdV方程

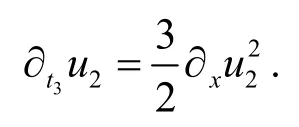
N=3時,非交換無色散Boussinesq 方程族的Lax 函數(shù)是 L=k3+u2k+u3,相應的非交換無色散Boussinesq 方程為:

非交換無色散GD 方程族的Lax 函數(shù)也可以表示為:

其中dressing 函數(shù)φ滿足

另外,式(3)等價于下述Sato 方程:

為了方便研究非交換無色散GD 方程族的附加對稱,引入Orlov-Schulman 函數(shù)Μ,假定函數(shù)

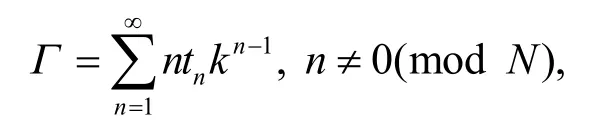
同時將Orlov-Schulman 函數(shù)Μ 定義為:

進一步計算,函數(shù)Μ 也可以用Lax 函數(shù)L 表示:

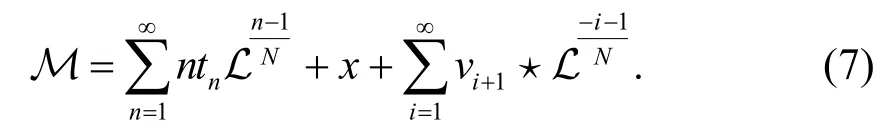
性質1函數(shù)Μ 滿足下列等式:

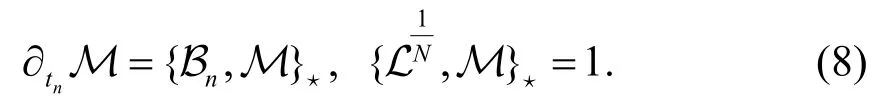
證明先證明第二個結論,

根據(jù) ?(eadY?X)=eadY?(?X)+{?YY,eadY?(X)}?,對方程(6)進行計算,

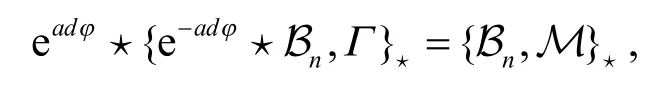
即為所求,證畢.

2 附加對稱

首先給出非交換無色散GD方程族的附加對稱.

定義1微分方程

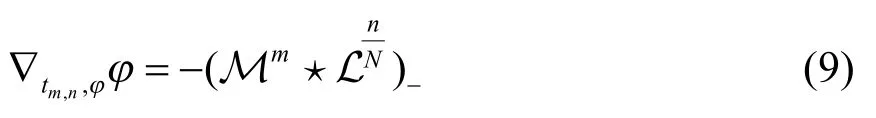
有了上述準備,現(xiàn)在來定義附加流,并且證明這些流是對稱的.類似于無色散KP 方程族的情形,引入附加變量并且定義作用在函數(shù)L 和Μ 上的附加流為:

定理1在非交換無色散GD 方程族中,只有滿足條件的附加流存活.

證明對于非交換無色散GD 方程族的Lax 函數(shù)(2)而言,它的負部等于0.根據(jù)式(10)有

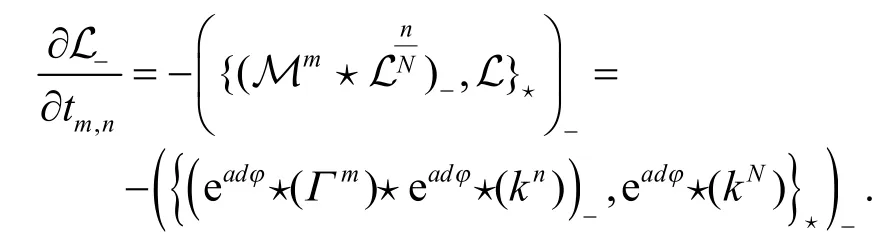
經過一系列計算,上述等式還可以寫為:

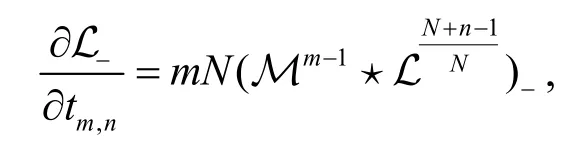
另外,非交換無色散GD 方程族中存活的附加流也有一些很重要的性質.

性質2在非交換無色散GD 方程族中,附加流和原始流交換,即,n≠0(modN).

證明將上式兩邊作用在Lax函數(shù)L 上,運用方程(3)和(10)有

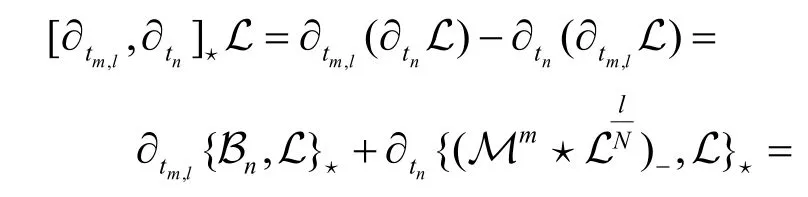
性質3非交換無色散GD 方程族的附加流可以形成無中心的 W1+∞代數(shù).

證明直接計算可以得到

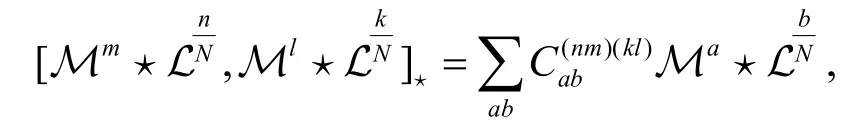
這意味著

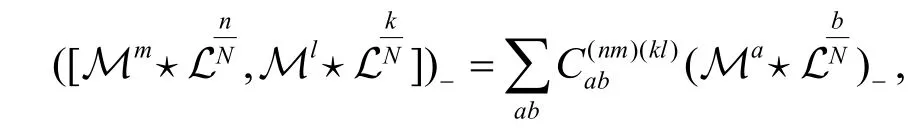
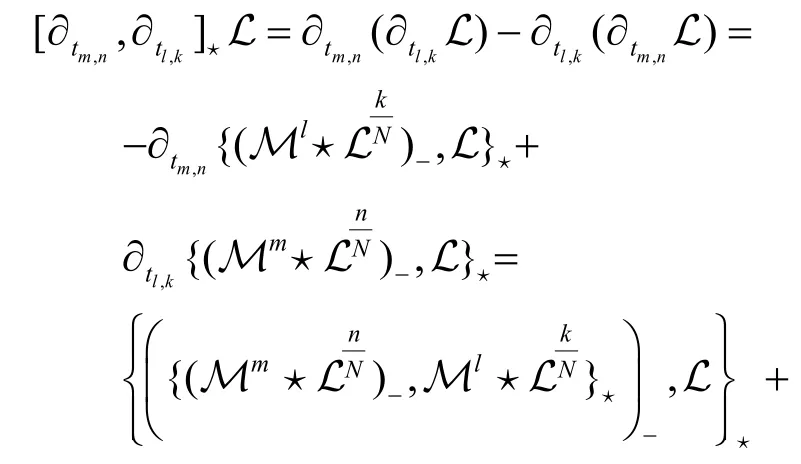
也就是說

3 弦方程

本節(jié)在非交換無色散GD 方程族附加對稱的基礎上,給出它的弦方程.

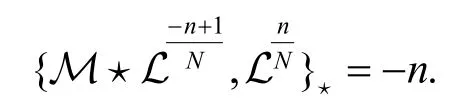
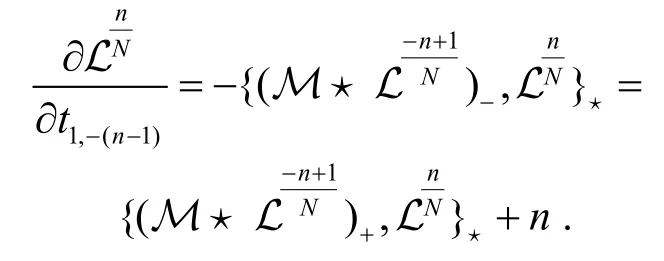
就是非交換無色散GD 方程族的弦方程.從上述推導中可以看出弦方程是指函數(shù)與附加變量無關的條件,即.

4 總結

本文主要研究非交換無色散GD 方程族的附加對稱及存活的附加流的性質.由于該方程族Lax函數(shù)的特殊性,只有滿足條件的附加流存活,這是與非交換無色散KP 方程族的一大不同.通過特殊附加流作用,得到弦方程.