基于改進蟻群算法的汽車混流裝配調度模型求解

李 燚 唐 倩 劉聯超 彭小剛 顏先洪

1.重慶大學機械傳動國家重點實驗室，重慶，4000442.重慶長安汽車股份有限公司，重慶，400023

0 引言

為了快速響應市場以及滿足消費者多元化的需求，汽車主機廠商普遍采用按照訂單生產的方式。具有“小批量、多品種、定制化”特點的訂單使得混流生產模式受到主機廠商的青睞，即在一條生產線上同時生產多種類型的車輛。但混流生產使得汽車裝配變得更加復雜，因為不同類型的車輛所需的零部件和對應的安裝工具不盡相同，導致裝配過程中每個工位針對不同車輛的安裝作業時間及具體作業內容都會發生變化。如果不建立合理的生產調度模型，不僅難以發揮混流生產的優勢，反而會降低生產效率，增加生產成本。

汽車混流裝配屬于一種典型的流水車間調度問題(flow shop scheduling problem，FSSP)，國內外學者針對該問題進行了深入研究，主要可歸納為調度模型的建立和多目標優化求解兩個方面。針對流水車間調度模型，魯建廈等[1]建立了最小化總調整時間和最小化空閑和超載時間的多目標優化模型。吳永明等[2]針對混流裝配線建立了最小化裝配線的生產節拍、站間平滑指數、演進平衡調整成本的調度模型。王炳剛等[3]深入研究了加工總切換時間最小化和零部件消耗平順化的調度模型。唐秋華等[4]則以零部件消耗均衡化、工位作業位置精準化以及車型調整費用最小化為優化目標。趙燕偉等[5]考慮車間工件工序、裝配工序等約束條件,以加工機器最小能耗為優化目標。DENG等[6]建立了最長完成時間和總延遲時間最小化的雙目標優化模型。LI等[7]和LU等[8]均建立了最長完成時間以及能量消耗最小化的雙目標優化模型。雖然上述調度模型具有一定的實際指導意義并解決了一些實際生產問題，但是并未考慮流水車間涉及大量的人工以及人機協同操作的情況，而這種情況在汽車混流裝配過程中真實存在，且往往會導致加工滯后以及裝配質量問題。

針對流水車間目標優化模型求解，目前廣泛采用智能優化算法，如人工蜂群算法[1]、粒子群優化算法[2]、遺傳算法[9]、候鳥優化算法[10]、果蠅優化算法[11]、粒子群優化算法[12]、灰狼優化算法[13]、鯨魚優化算法[14]等，上述算法在求解相應的目標優化模型時均取得了不錯的效果。近年來，蟻群算法[15]因其獨特的正反饋求解機制受到不少學者的青睞，被應用于求解多目標優化問題，如ZUO等[16]使用蟻群算法求解云制造中的多目標優化問題，REED等[17]和KUMAR等[18]將其應用于車輛路徑規劃問題，PEREZ等[19]將其應用于求解無人機的軌跡，均取得了很好的結果。本文建立了瓶頸選裝工位負載平衡化、考慮換裝與提前作業時間的加工滯后次數最小化的分層序列雙目標優化模型，并設計了一種改進蟻群算法進行求解，以解決汽車混流裝配過程涉及大量人工以及人機協同操作而導致工位過載、整車裝配質量無法得到保證的問題。

1 問題描述與建模

1.1 問題描述

汽車總裝車間由一條主裝配線和多條分裝配線組成，其中分裝線是為了將某些零件裝配在一起形成部件總成，然后按照排產順序同步輸運送到主裝配線上的特定工位與對應車輛進行裝配，從而提高裝配效率，如變速器分裝線、底盤合裝分裝線、儀表分裝線等。本文以主裝配線為研究對象，在主裝配線上，車輛通過滑撬或者吊具以一定的速度勻速通過流水線上各個工位，然后工位上的兩邊布置工人或者機器人進行相應的裝配作業。由于總裝車間的裝配線大部分工位涉及人工操作以及人機協同工作，同時訂單排產時最小生產循環中的生產車輛車型、配置不同，導致在裝配流水線的每個工位不僅安裝的零件種類、型號繁多，而且裝配作業內容以及所耗費時間也不同。如果不建立合理的混流裝配調度模型從而得到合適的生產序列，不僅難以保證生產線負荷平衡從而導致生產效率低下，更無法保證裝配工藝造成整車裝配質量參差不齊的情況。

1.2 模型的建立

首先對汽車混流裝配過程作以下假設：①排產車輛序列一旦確定就不能中途任意更改，否則會導致分裝線上的零部件總成和待裝配車輛匹配錯誤，造成生產線停線；②邊線的物料供應都可以按時送達，不會因物料供應問題而導致各工位上的裝配任務暫停；③每個工位在同一時間內只能對一輛車進行加工作業。所建立的數學模型涉及的參數定義見表1。

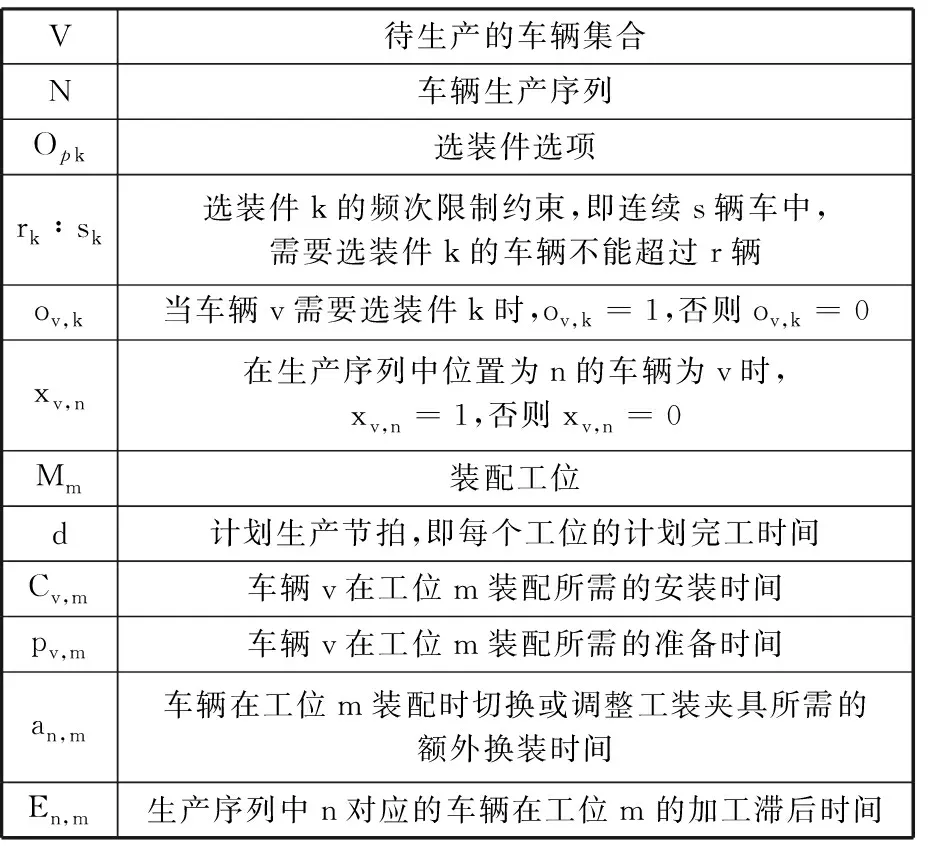
表1 模型參數定義

1.2.1瓶頸選裝工位負載平衡化模型

在混流裝配流水線上存在某些瓶頸工位，如果該工位上連續多次裝配某類型的選裝件會導致負荷超載，即當前工位無法在規定時間內完成對應的裝配工作，導致生產線停線，影響生產節拍，因此，需要對該工位某類選裝件的連續裝配次數做出限制(表1中rk∶sk)。以天窗選裝件為例，車輛的配置中可分為全景天窗、普通天窗、無天窗三類。當裝配的車輛無天窗時，該工位無需任何操作，處于閑置狀態，但是該工位連續裝配全景天窗時，會出現相關工位過載情況。針對全景天窗選裝件的頻次限制設定為2∶3(見表2)，即連續生產的3輛汽車中，選裝全景天窗的車輛數目不能超過2。

表2 全景天窗安裝頻次限制

假設部分待生產序列(即對應的全景天窗選裝情況)如表3所示。表中第2行值為0時，表示該對應序列位置的車輛不需要全景天窗選裝件，即ov,k為0；當需要安裝全景天窗時，ov,k為1，明顯可知，序列中的2、3、4位置對應的3輛車超出了選裝件頻次限制。假設待裝配的車輛集合為V，排好的生產序列為N，則兩者應滿足的關系為

(1)

其中，xv,n={0,1}，上式保證待裝配的車輛在生產序列中只能且必須出現一次，符合流水裝配線加工需求。選裝工位的過載約束數學表達式[20]如下

(2)

?k∈Opn=sk-1,sk,…,N

xv,n′∈{0,1}ov,k∈{0,1}

該問題屬于典型汽車排序問題[21]，GENT[22]將其轉化為哈密頓路徑問題，TAMAS[23]將其轉化為集合覆蓋問題，從而證明其為NP-hard問題，即無法在多項式時間內求解。本文將其轉化為優化模型，以便后文使用改進蟻群算法進行求解，具體表達式為

(3)

1.2.2最小化工位加工滯后次數模型

以待裝配序列中位置為n的車輛在流水裝配線工位m上完成相應的裝配作業為例，涉及人工及人機協同操作的每個工位具體工作流程可分為以下兩部分：

(1)準備過程。當完成上一個裝配作業后，首先需要進行短暫的休息，然后通過查看工位旁的看板確定下一輛車所需的零部件類型，并從線邊庫存中挑選對應的零部件，最后調整或更換對應的裝配工具。其中，休息時間和查看并挑選零件的時間為pm，為固定值。但若前后車輛在該工位所裝配的零件不同時，則需要花費額外的時間an,m來切換或者調整安裝工具，其表達式為

an,m=tm

(4)

其中，tm為更換或者調整安裝工具所花的時間，與工位有關。當前后車輛裝配的零件型號尺寸相同時，an,m=0。

(2)安裝過程。操作工人完成當前工位所需的裝配工作。假設車輛v在當前工位的安裝時間為Cv,m，則在車輛序列中為n的車輛安裝時間為

安裝時間與工位以及安裝的零件有關。所以裝配所花費的時間為

傳統的柔性流水車間調度問題(flexible flow shop scheduling problem, FFSP)中，n個訂單在m個工位上加工，每個訂單在各個工位上加工所需的時間di,j(i=1,2,…,n；j=1,2,…,m)不同，所以生產線的生產節拍應該滿足的條件為

d≥maxdi,j

(5)

與傳統流水線加工不同，在汽車混流裝配流水線中，車輛通過滑撬或者吊具在流水線上以均勻的速度通過，每個訂單在各個工位上加工所需的計劃時間di,j(i=1,2,…,n；j=1,2,…,m)相同。所以d表示每個工位的生產周期，同時也表示混流裝配線上的計劃生產節拍。

在任意工位，前一輛車出現加工滯后情況時，為了滿足生產要求，下一輛車的裝配準備過程所需的時間pm會被壓縮，使得工人沒有足夠的休息時間或者來不及做準備工作，從而影響車輛的裝配質量。當處于汽車銷售旺季時，生產節拍會達到甚至超過最大設定值，使得生產線處于超負荷運行狀態，此時d會設置為更小的值，從而進一步壓縮準備時間pm。

在實際生產過程中，與傳統的流水車間調度模型不同的是工人操作比較靈活，在計劃完工時間d內完工的情況下，可提前開始下一輛車的裝配工作。提前時間與工位有關，設為Um。所以該車輛在工位m的加工裝配滯后時間表達式為

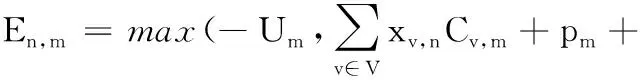
(6)

其中，E1,m=0，明顯可知En,m值為正表示當前工位的車輛加工滯后，Ev,m為負意味著當前工位作業提前完成。

舉例說明，假設計劃生產節拍d=60 s(本文默認的時間單位為秒)，Um=3 s，pm=8 s，更換夾具時間tm=5 s，部分生產序列中的車輛型號為{A,B,C,D,A,B,C,D},對應的安裝時間為{52,50,44,45,52,50,44,45}，加上準備時間和更換夾具的時間后為{60,63,57,58,65,63,57,58}，對應的加工裝配滯后時間為{0,3,0,-2,3,6,3,1}，明顯可知該生產序列中有5輛車加工滯后。但若將生產序列中的車型更換為{A,C,B,C,B,D,D,A}，則加工裝配滯后時間為{0,0,-3,0,-3,0,-3,-3}，沒有車輛出現加工滯后情況，其中還有4輛車可以提前完成加工。所以，后者生產序列優于前者。車輛序列中的加工滯后次數統計表達式為

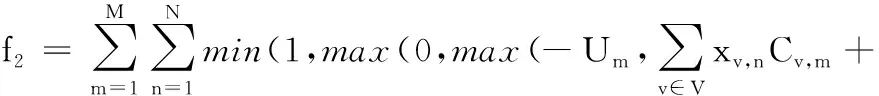
(7)

結合式(1)、式(3)和式(9)，最終本文所建立的分層序列雙目標優化模型為

(8)

首先優化f1，然后在f1取得最優值(或者近似最優值)的解集合中確定f2取得最小值對應的解，即尋找滿足f2取得最優值的同時滿足f1也取得最優值的解。需要說明的是，選裝件選項的分類和車型配置的分類并不完全相同，假設三種車型A、E、H選裝件類型相同，如果得到的生產序列為{A,B,C,D,E,F,G,H}，則隨意調換A、E、H的位置，f1的值保持不變，但是f2的值不盡相同。

2 改進的雙目標蟻群算法介紹

2.1 基本原理

當前針對車間調度的優化問題往往采用智能啟發式算法，如混合啟發式算法[24]、遺傳算法[25]。近年來蟻群算法[26]可有效地解決NP-hard相關的優化問題，尤其是旅行商、車間調度等問題，受到學術界和工業界的廣泛關注。

本文針對分層序列雙目標優化問題所設計的改進蟻群算法的求解思路為：將待生產的車輛視為一系列的節點，螞蟻首先隨機選擇一個節點作為起始點，然后根據轉移概率規則(信息素、啟發式信息共同作用)逐一選擇下一個節點，直至所有節點被選擇完成，最終形成的節點序列即為所求的一個可行解。然后對可行解中的相鄰節點進行信息素局部更新。當種群中所有螞蟻完成上述操作之后，會存在多個可行解，構成一個解空間。在解空間中尋找最優序列，并將最優序列的相鄰節點進行信息素全局更新。最優序列的判定規則如下：在當前解空間內，尋找優化目標函數一取得最優值的可行解，如果存在多個目標函數一取得最優值的可行解，則選擇其中滿足優化目標函數二取得最優值的解。通過不斷的迭代，最終得到全局最優解或者近似最優解。算法具體流程見圖1。

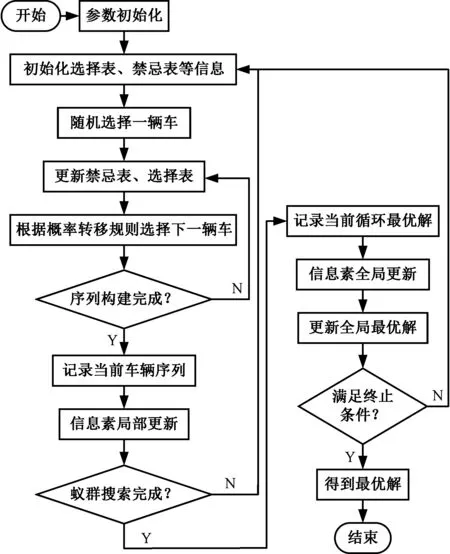
圖1 改進蟻群算法流程圖Fig.1 Improved ACO algorithm flow chart

2.2 算法參數定義

本文設計的改進蟻群算法涉及的參數定義見表4。

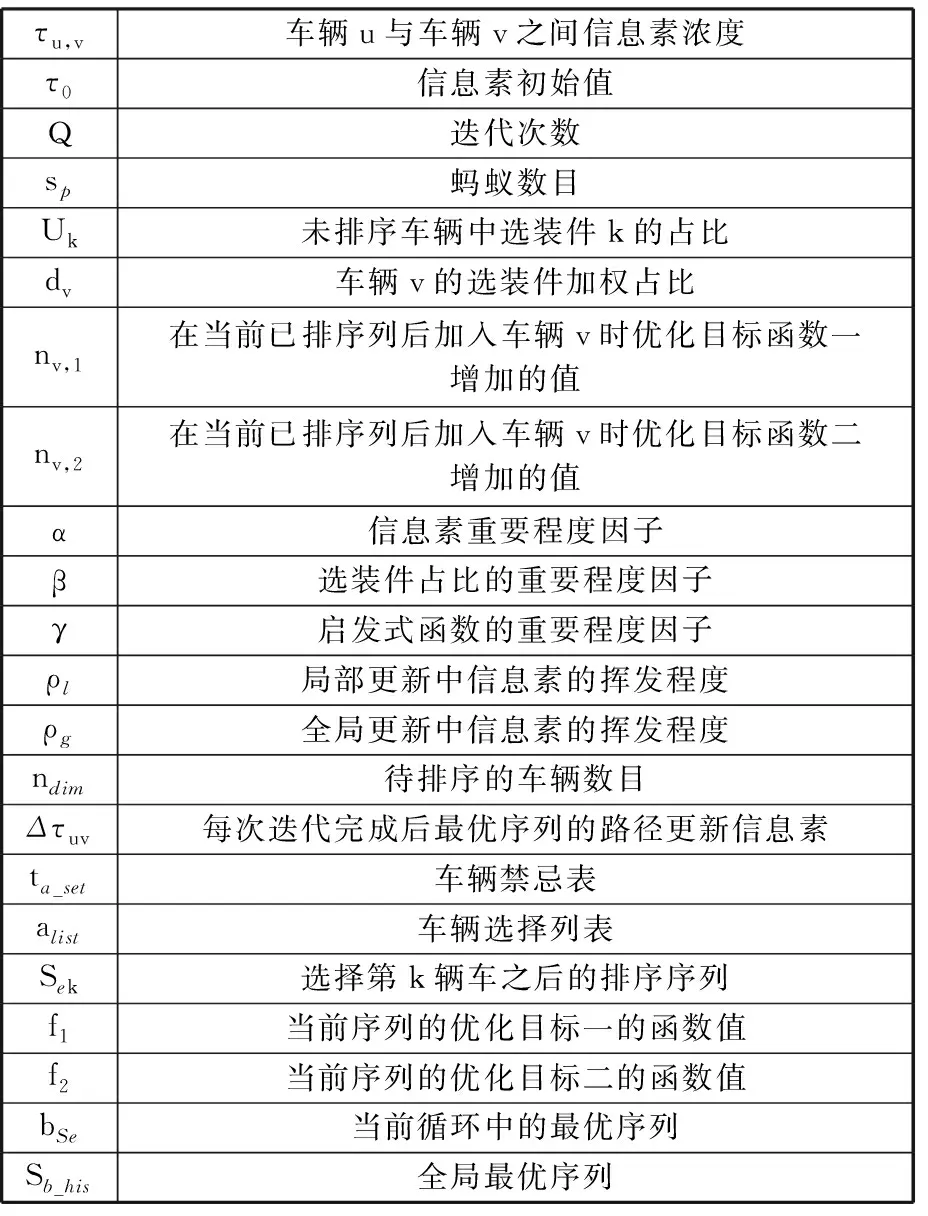
表4 算法參數定義

2.3 信息素更新

τu,v表示車輛u和v之間的信息素，而信息素更新過程分為局部更新和全局更新。當每只螞蟻構建完成一個可行解即車輛生產序列之后，對該序列中的相鄰節點進行信息素局部更新，局部更新表達式為

τu,v(t)=ρlτu,v(t)+(1-ρl)τ0

(9)

其中，ρl取值范圍為[0,1]，τ0為信息素濃度初始值。局部實時更新的目的是減少已選擇節點之間的信息素濃度，避免之后的其他螞蟻做出同樣的決策，從而保持了選擇的多樣性，避免陷入局部搜索。

當種群中所有的螞蟻構建完成可行解，形成一個解空間，然后確定當前解空間中最優可行解。最優解的具體評價方式為：首先尋找在當前解空間中第一優化目標取得最優值的序列，如果存在多個序列，則在其中尋找第二優化目標取得最優值的序列。然后對該序列中的相鄰節點進行信息素全局更新，更新表達式為

τu,v(t+1)=ρgτu,v(t)+(1-ρg)τu,v(t)

(10)

其中，ρg取值范圍為[0,1]，而τu,v(t)的表達式如下：

(11)

式中，f1、f2分別為當前解空間中最優可行解所對應的第一優化目標和第二優化目標函數的值。

通過全局更新規則，可保證將當前循環中最優序列的整體信息反映到信息素上，指導后續搜索過程，形成正反饋機制。

2.4 概率轉移規則

假設某只螞蟻在構建可行解過程中，當前已有序列中的最后一個輛車為u，然后從待排序的車輛集合alist中選擇下一輛車v，轉移概率規則如下：

(12)

其中，q0為[0,1]區間的參數，q為[0,1]區間均勻分布的隨機數，su,v的具體表達式為

(13)

其中，nv,1和nv,2分別為在已有車輛序列中添加車輛v之后的優化目標函數一和目標函數二的變化值。當q>q0時，計算待排序中每輛車的選擇概率，然后采用輪盤賭方法選擇車輛v。概率計算公式為

(14)

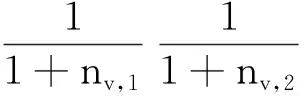
(15)

式中，xv,k為常數0或1，表示當前車輛是否有選裝件k；Uk為選裝件k在剩余待排序的車輛的占比。

該算法具有以下優點：①該算法整個過程為正反饋機制，從而使得搜索過程不斷收斂并逼近最優解；②加入啟發式規則后有效地克服了傳統蟻群算法容易陷入局部最優的問題；③概率轉移規則中加入選裝件加權占比規則，可使第一優化目標得到快速的收斂。

3 仿真實驗及結果

3.1 仿真實驗

以某主機廠的總裝車間為例，混流裝配過程每個最小生產循環中共36輛車，其中共有9種不同的車型配置(用字母A～I表示)，每種車型配置有4輛車。主裝配線上選取3個典型的瓶頸選裝件，對應的頻次限制以及每種車型配置對應的選裝情況見表5。其中，數字0代表對應的車輛未裝配相應的選裝件；數字1代表需要裝配對應的選裝件。

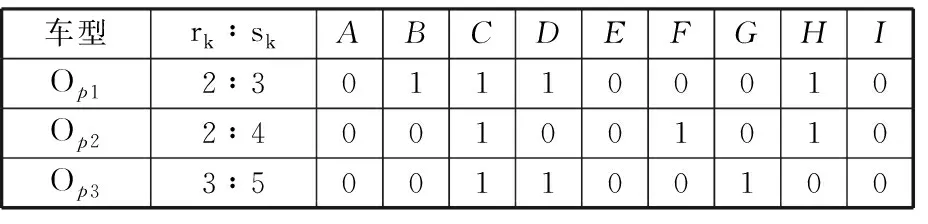
表5 車型瓶頸選裝件

同時選取流水裝配線上的某8個連續安裝工位為例，車輛在各個工位上的裝配作業所需的安裝時間見表6，車輛在各個工位所需的工具類型見表7。

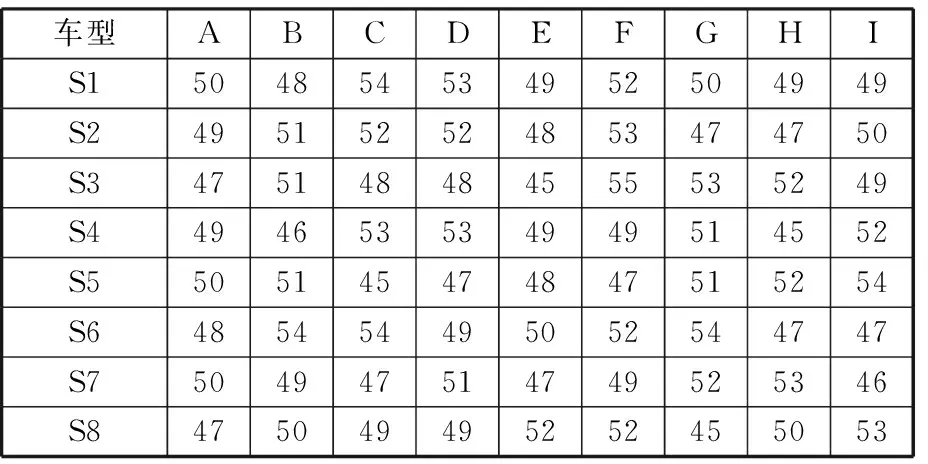
表6 工位安裝時間

需要說明的是，表7不同工位中相同的數字并不代表相同的安裝工具，該羅馬數字用于說明在單個工位中各種類的車輛是否使用不同的工具。各個工位調整工具的時間見表8。

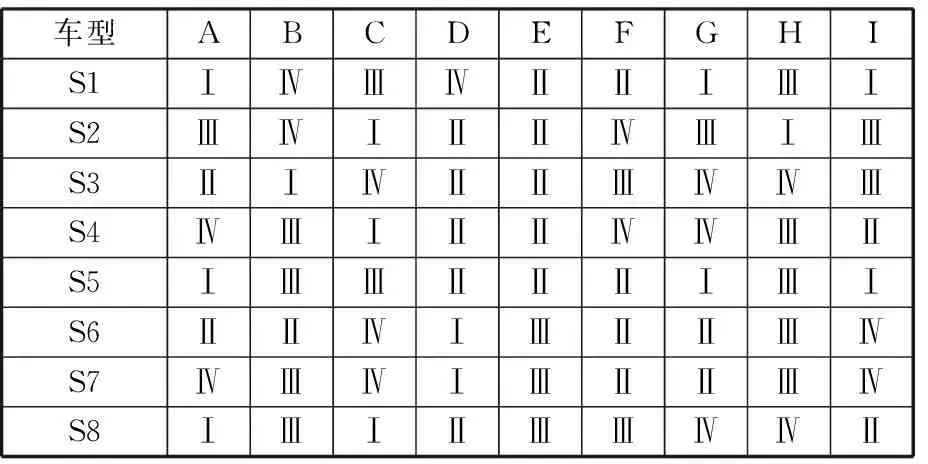
表7 工位安裝所需工具型號

表8 工位切換工具時間

生產節拍d=60 s，各個工位提前裝配作業時間U=3 s，準備時間p=6 s。實驗過程中改進蟻群算法的參數取值見表9。

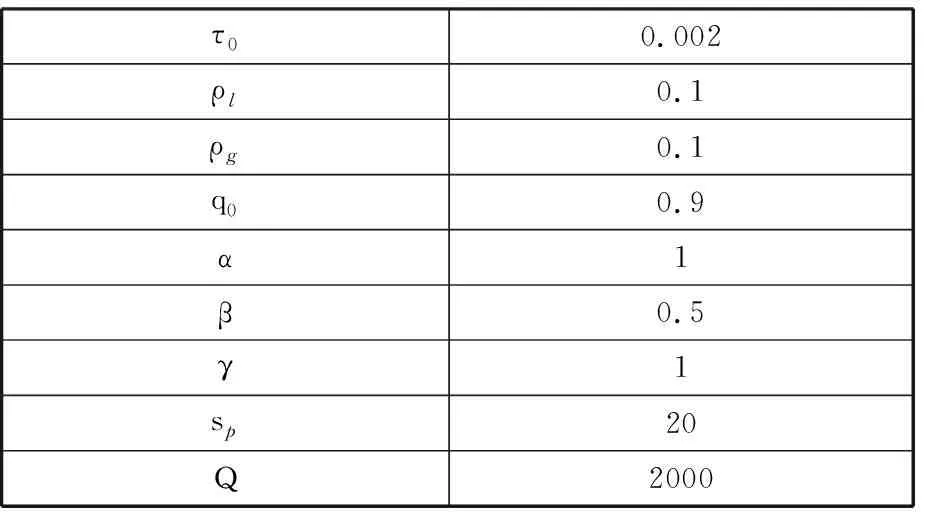
表9 算法參數取值

3.2 實驗結果

將本文采用的改進蟻群算法和傳統蟻群算法、對比遺傳算法[26]各計算10次，并記錄迭代過程中的優化目標函數值以及最優解。目標函數一在前10次迭代過程中的平均值變化情況如圖2所示，最優解對應的目標函數一的取值如圖3所示。同理，在整個迭代過程中，目標函數二在迭代過程中平均值的變化情況如圖4所示，最優解的目標函數二的變化情況如圖5所示。

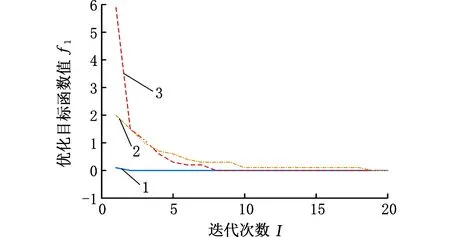
1.改進蟻群算法 2.對比遺傳算法 3.傳統蟻群算法圖2 目標函數一的收斂曲線平均值Fig.2 Mean value of convergence curve of objectivefunction one

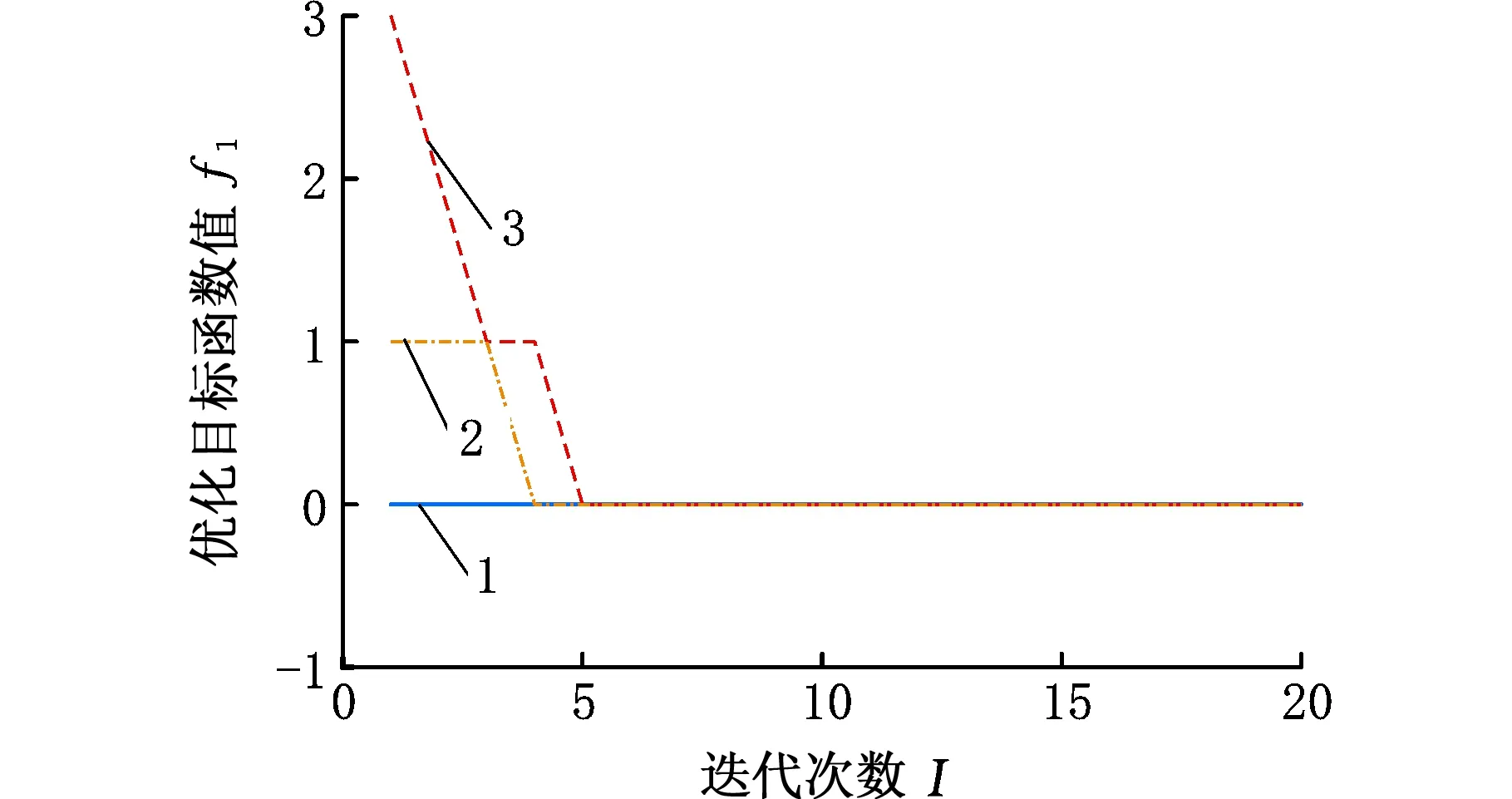
1.改進蟻群算法 2.對比遺傳算法 3.傳統蟻群算法圖3 最優解對應的目標函數一的收斂曲線Fig.3 Convergence curve of the objective functionone corresponding to the optimal solution

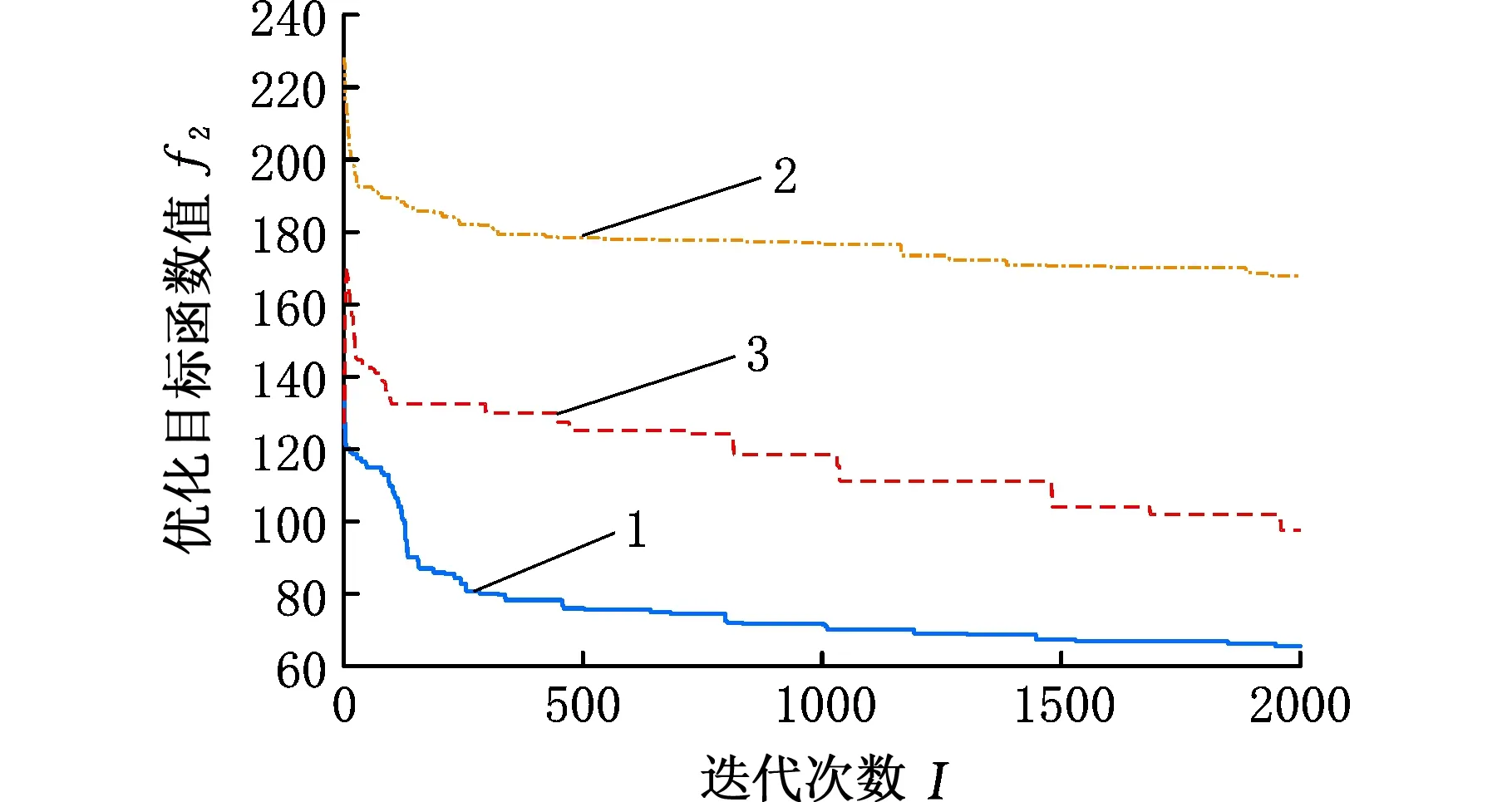
1.改進蟻群算法 2.對比遺傳算法 3.傳統蟻群算法圖4 目標函數二的收斂曲線平均值Fig.4 Mean value of convergence curve of objectivefunction two

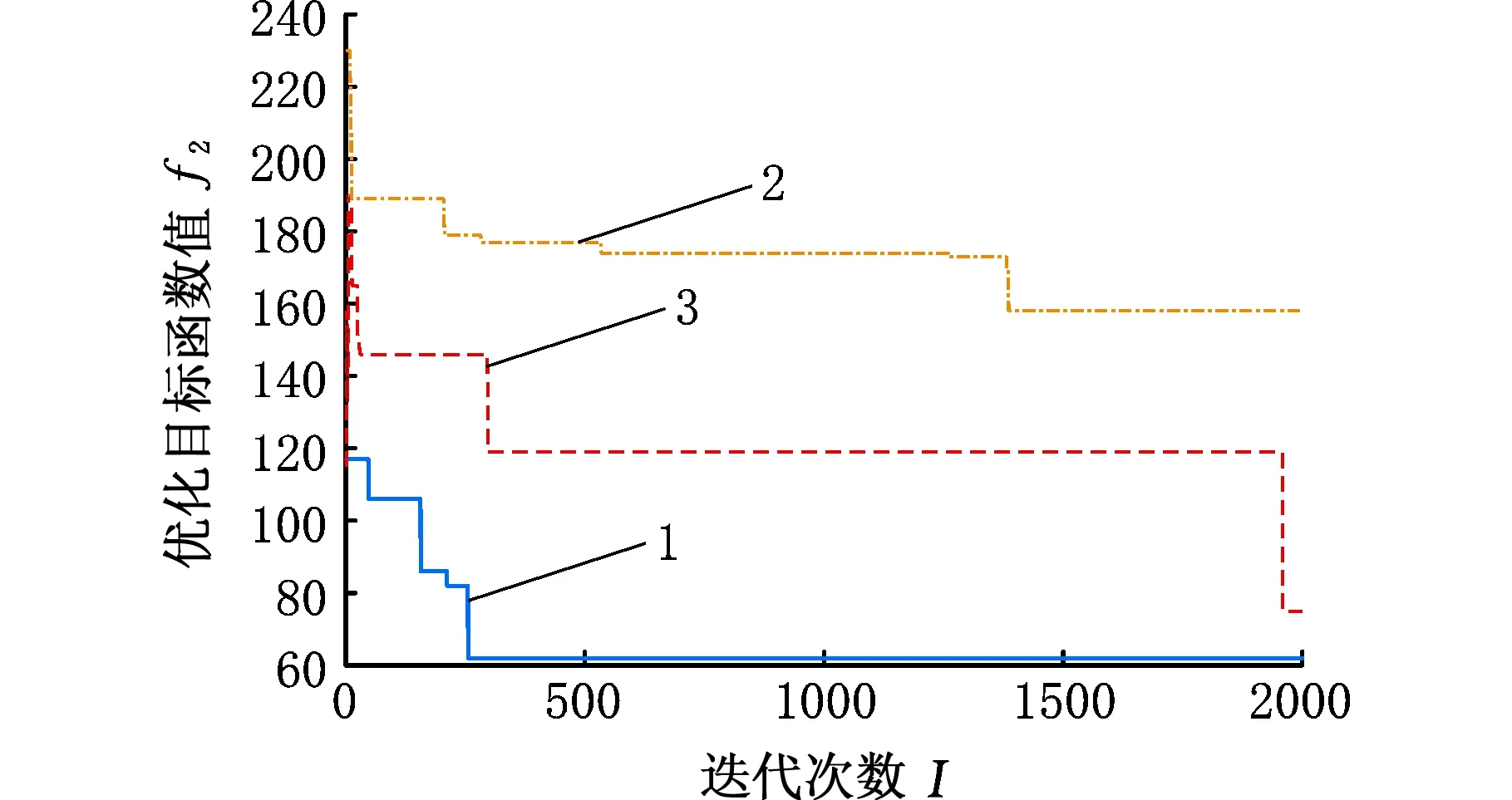
1.改進蟻群算法 2.對比遺傳算法 3.傳統蟻群算法圖5 最優解對應的目標函數二的收斂曲線Fig.5 The convergence curve of the objective functiontwo corresponding to the optimal solution

由圖2、圖3可知，在優化第一目標函數過程中，即瓶頸選裝工位負載平衡化時，相比傳統蟻群算法，使用改進蟻群算法收斂得更快；由圖4、圖5可知，在優化第二目標函數過程中，即最小化工位加工滯后次數時，本文算法不僅收斂得更快，而且收斂的效果也更好。具體統計結果見表10。

當設定不同的計劃生產節拍時，使用本文所設計的改進蟻群算法計算10次之后求解得到的各個目標函數的最優值和平均值見表11。由表11可知，當計劃生產節拍設定時間大于或等于63 s時，可保證瓶頸選裝工位負載平衡化以及考慮換裝與提前作業時間的加工滯后次數為0，從而保證了整車裝配質量。

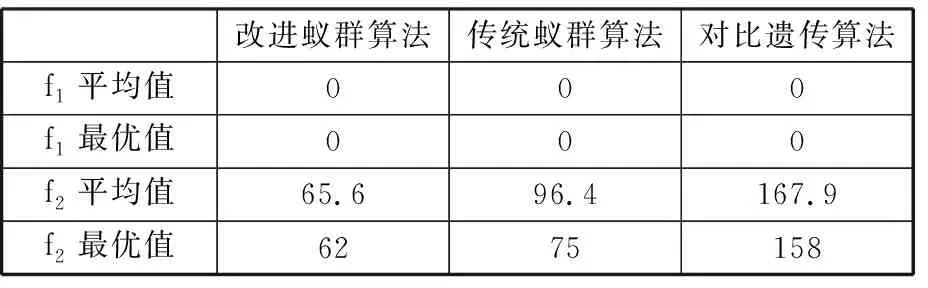
表10 實驗結果對比

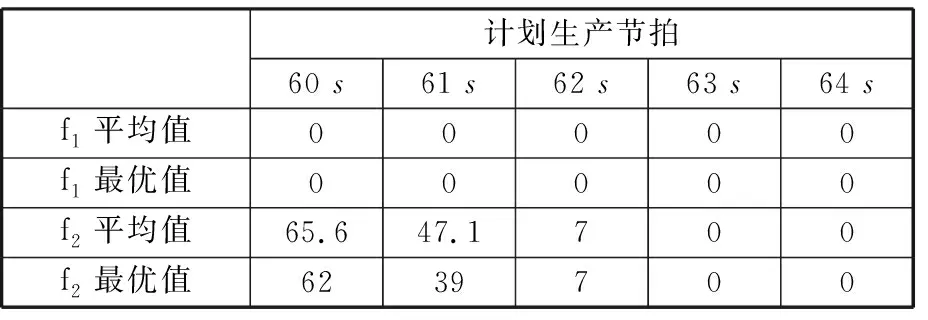
表11 不同的計劃生產節拍對應的優化目標值

4 結論

(1)本文面向汽車混流生產模式下的流水裝配線，為了保證生產節拍以及整車裝配質量，建立了瓶頸選裝工位負載平衡化和考慮換裝與提前作業時間的工位加工滯后次數最小化的分層序列雙目標優化模型。

(2)設計了一種改進的蟻群算法用于求解所建立的優化模型。為了快速優化瓶頸選裝工位負載平衡化目標，添加選裝件加權占比啟發式規則；為了保證所求的解不但使第一優化目標函數取得最優值，而且使得第二優化目標也取得最優值，設計一種特殊的啟發式函數用于轉移概率計算以及信息素全局更新，同時更改最優解的評價方法。

(3)采用某汽車主機廠實際生產相關數據進行仿真實驗，驗證了本文算法和模型的有效性；此外，該算法可以反向求解在瓶頸選裝工位負載平衡化目標函數取得最優值的情況下工位加工滯后次數為0的計劃生產節拍，具有一定的生產指導意義。