基礎油中金剛石納米顆粒潤滑性能和導熱性能的分子動力學分析*

冷岳峰 王嵩博 劉運宇 李 強

(遼寧工程技術大學機械工程學院 遼寧阜新 123000)

分子動力學(MD)模擬方法是研究熱輸運特性最有效的工具之一，特別是對于基于晶格動力學方法的復雜結構，其計算能力非常強大。LAMMPS是一種可對處于三態的粒子團進行建模的分子動力學代碼，它可以使用各種原子間勢和邊界條件對原子、聚合物、金屬、陶瓷、氧化物、顆粒或宏觀系統進行建模[1]。

原子結構是影響金剛石、石墨烯、碳納米管等重要的因素，利用原子間原子勢的原子模擬方法是研究碳原子結構最有效的方法之一。但必須要有可靠的原子間勢才能研究發現各種基本物理性質，如結構性質、表面特性、熱特性等。現有的文獻表明[2-3]，納米顆粒的含量、分散納米顆粒的大小和形狀、納米流體的溫度以及分散納米顆粒的分布等因素都會影響納米流體的熱性能。這些因素中的每一個都是納米流體傳熱現象廣泛研究的來源，從而促進了該領域知識的發展。

納米流體的概念最早是由DAI[4]在20世紀90年代中期提出的，作為一種替代微米級固體的方法，這些固體被用于傳統的冷卻劑中以提高其導熱性。研究人員致力于進一步了解支配納米流體的物理學，包括使用不同的方法計算各種類型納米流體的熱導率，以及研究熱的機制。與傳統流體相比，納米流體具有更高的導熱系數、更好的對流換熱以及更低的壓降，這使得納米流體成為一種具有良好傳熱潛力的新技術。

SUKKAR等[5]將球形氧化銅納米粒子和氧化鈦粒子添加到潤滑油中，研究了不同質量分數的納米粒子在潤滑油中的導熱性，結果表明，納米氧化銅顆粒對潤滑油導熱性能的提升優于氧化鈦；當納米粒子質量分數為0.1%時，含納米氧化銅和氧化鈦潤滑油的導熱系數分別增加了7.27%和4.54%。XIE等[6]研究了碳納米管體積分數對納米流體熱導率的影響，發現碳納米管使納米流體導熱系數提高了7%～20%。ASSAEL等[7]研究了在2種不同分散劑作用下碳納米管水懸浮液的熱導率，發現十六烷基三甲基溴化銨(CTAB)表面活性劑使得懸浮液導熱系數增長了8%。HWANG等[8]研究了質量分數0.5%碳納米管在礦物油基底液中的熱導率，結果表明潤滑油的熱導率增加了9%。GARG等[9]采用超聲波研究了碳納米管對水基納米流體傳熱性能的影響，發現質量分數1%碳納米管可使水基納米流體的導熱系數提高20%。SINGH等[10]研究了碳納米管對水-乙二醇納米流體熱導率的影響，發現質量分數0.4%的碳納米管使得納米流體熱導率提高了72%。

李春風等[11]對富勒烯、石墨烯、金剛石、碳納米管和納米石墨的摩擦學性能進行了歸納總結，發現1%的富勒烯便可有效降低石蠟油摩擦因數33%；含5%富勒烯的石蠟油潤滑下鋼球磨斑直徑可降低33%，摩擦因數降低了20%。ZHANG等[12]研究了棕櫚油、大豆油、菜籽油分別作為MQL基礎油的潤滑性能，證明了3種植物油的潤滑效果差異很小，摩擦因數只有0.04的差異，與液體石蠟相比都具有較低的摩擦因數。但是大豆油相比其他2種植物油，具有較低的黏度，更適合作為NMQL的基礎油。

目前的文獻都是針對一些水為基礎液進行的分子動力學仿真，對基礎油液加入金剛石納米顆粒及其他碳結構的納米顆粒研究較少。本文作者以蓖麻油酸為基礎潤滑劑，以金剛石納米顆粒為添加劑，采用Tersoff勢描述金剛石原子之間的勢函數，進行了分子動力學仿真，研究了加入不同體積分數和不同粒徑的納米顆粒對潤滑性能以及熱導率的影響。

1 研究方法和數學模型

1.1 研究方法及理論基礎

熱傳導是溫度梯度引起能量傳遞的現象，屬于非平衡過程。另一種計算熱導率的方法就是基于非平衡分子動力學的模擬[13]。在該方法中，首先通過某種方式建立一個溫度梯度，并等待足夠長的時間，使得系統達到穩態。在達到穩態后，對系統的溫度梯度和非平衡穩態熱流進行測量，然后就可以根據傅里葉定律來計算熱導率。

在此非平衡態研究熱導率方法中，系統的總能量近似為

(1)

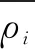
在參數優化的過程中，需要有正確的生成能和晶格常數。然而，僅用目前的方法很難得到具有正確晶格參數值的碳結構。此外，考慮到金剛石鍵合特性各不相同，試圖用一種常見的勢函數來描述內部原子的相互作用是不可取的。因此，有必要把金剛石和外部油液的相互作用分開，用不同的形式來描述它們。因此，最終決定用Tersoff形式描述金剛石原子之間的相互作用；用Lennard-Jones勢來描述層間相互作用。根據Lennard-Jones作用勢，原子間的相互作用[14]如下:

(2)

式中：εij表示力的強度的參數；σij表示原子大小的參數；r表示原子之間的距離。

基于文獻[3,15]的研究結果，文中熱導率的研究方法運用了速度重標法。當系統達到穩態之后，開始逐漸地增加熱源中粒子的速率，并且對熱源中的每一個粒子i，作如下速度轉換

(3)

式中：vc是熱源粒子的質心速度，

(4)

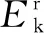
(5)

Δε是一個常數，該常數等于熱源中能量的增量，

(6)

如果每 Δt作一次速度變換，則產生的熱流密度大小為

(7)

其中，A是模擬系統在垂直于傳導方向的橫截面積。當使用周期性邊界條件時，應當將該熱流除以 2，因為當在某一位置注入熱量時，熱量將從熱源區域兩邊流出，每一邊流出的能量是總量的1/2。在系統達到平衡穩態之后，開始測量溫度梯度，然后根據傅里葉定律計算非平衡態熱導率。

1.2 物理模型和參數配置

圖1給出了以蓖麻油酸為潤滑劑的分子動力學模型，模型分為上下壁面，上壁面為金剛石，下壁面為金屬鎳，中間為蓖麻油酸分子以及內部的納米金剛石顆粒。現以下壁面Ni原子層固定不動，上壁面的金剛石層以10 m/s的速度向右側移動，同時對上壁面施加一個穩定的壓力，以10 m/s的速度壓縮，對摩擦過程進行模擬，用來模擬壓縮和滑移時的過程。

在上下兩層壓縮面之間建立蓖麻油酸分子團尺寸為20 nm×10 nm×10 nm的基礎流體，上下壁面為2 nm。金剛石納米粒子的直徑為4 nm，建立的模型總的原子數為22 584個。

模擬計算采用聯合力場勢函數，在x、y方向上采用周期性邊界條件，在z方向上采用非周期性邊界條件。在分子動力學模擬中，在有限溫度下進行的實驗中經常發現，金剛石結構在高溫破壞或轉變為其他結構之前應該是穩定的。

圖1 低體積分數金剛石納米顆粒潤滑油的分子動力學模型

在具有周期性邊界條件的直徑4 nm的球形金剛石結構樣品上進行了模擬。在模擬中，所有的性能計算都是在253 K左右溫度下進行的。在253 K的條件下，經過300 ps時間步后，進行徑向分布函數(RDF)的分析。在以前的研究中已經發現，如果一個結構不是穩定的，在幾千個MD步驟內，原子結構很快會發生崩潰。因為布朗運動的作用，納米粒子周圍表現出較高的不穩定性，納米粒子受到的布朗運動更加劇烈，對減摩性能有較大影響。

模擬過程中需要進行3個步驟：弛豫、壓縮和剪切。首先進行弛豫，控制在253 K的溫度下，采用聯合力場，金剛石納米粒子采用Tersoff勢函數，鎳單質采用EAM勢函數，截斷半徑選取7.0，充分弛豫。施加壓力，上壁面以10 m/s的速度壓向下壁面。采用周期性的邊界條件，模擬采用的計算方法為Verlet法，時間步長選定為0.1 fs。采用Nose-Hoover控溫的方法，在NVT系統下對所有的原子進行弛豫，通過改變壓力與溫度以及納米顆粒的粒徑大小，文中重點考察不同條件下對薄膜潤滑的原子分布、滑移特性和分子團聚特性的影響。

2 模擬驗證及其討論

2.1 數密度分析

當系統中存在固液氣三態相交時，數密度可以很好地給出分界附近的結構性特點。粒子數密度的不均勻性導致粒子的輸運也就是擴散現象。圖2所示為中心壁面區域油膜厚度的原子數密度分布，可以發現近壁面區域的原子呈層狀散布，這說明近壁面附近存在油膜吸附層。

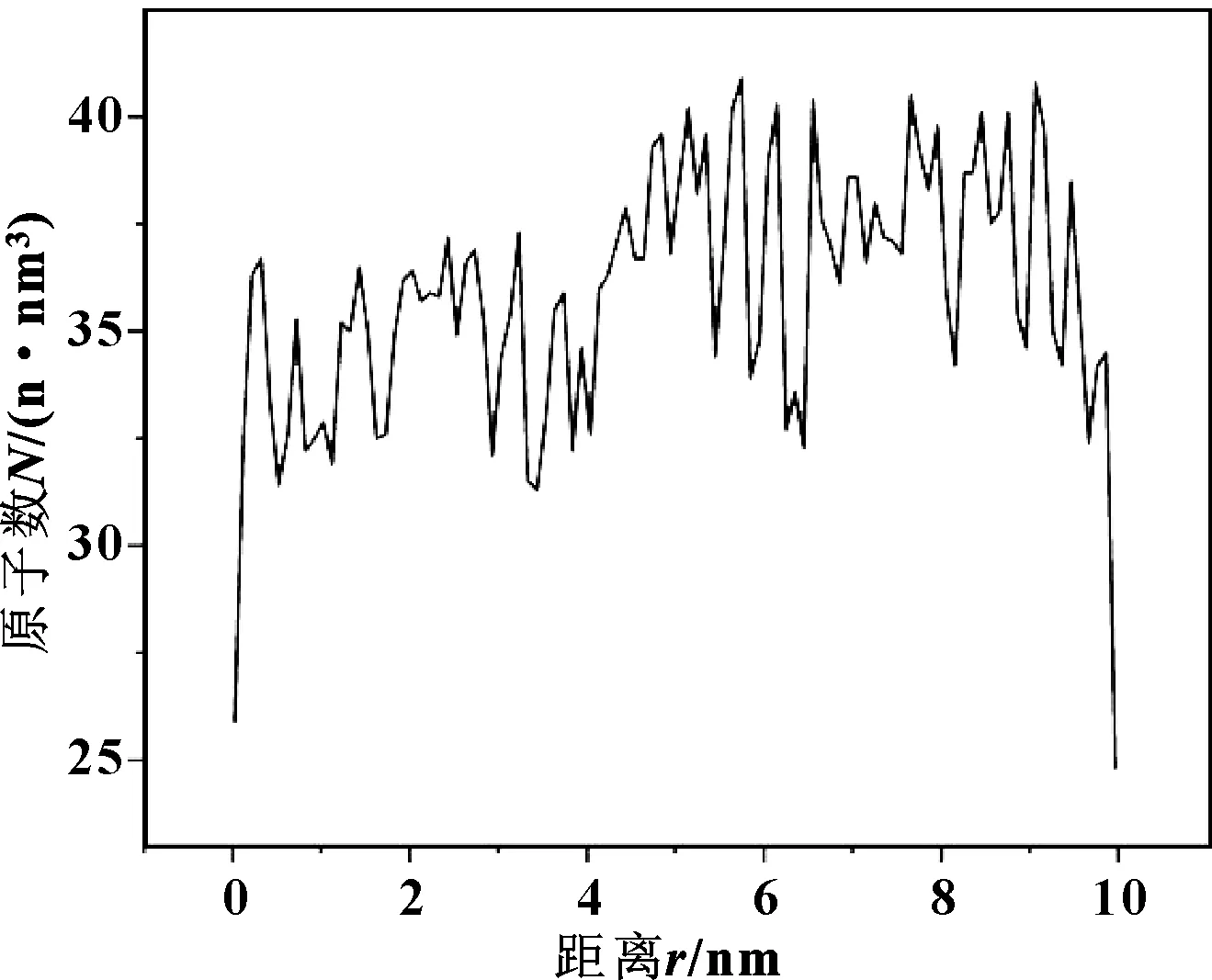
圖2 中心壁面區域沿y軸的原子數密度分布

從圖3中可以看出，金剛石顆粒周圍存在吸附層，納米粒子周圍的密度較大，潤滑劑附著在金剛石納米顆粒上，當納米顆粒被壓扁時，這層薄膜也未被破壞。由此，可以認定金剛石顆粒周圍的吸附層會對潤滑劑分子產生影響，有可能會改變局部的密度等。另外，如果油膜相對比較厚，這種情況下的影響基本可以忽略，但對于比較薄的潤滑膜，這種影響還是比較大的，不能忽視。

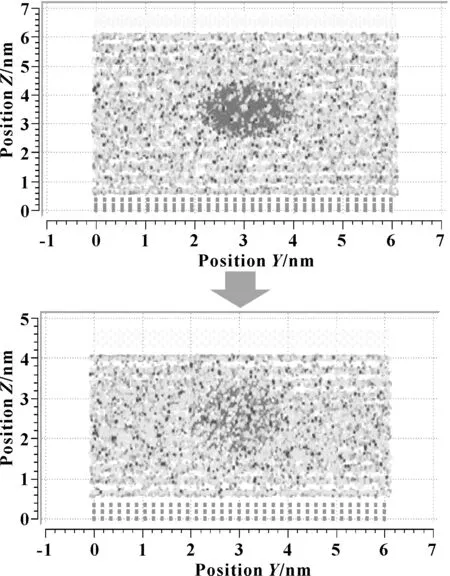
圖3 壓縮過程中納米粒子的壓扁狀態和邊界油膜吸附層

從圖3中還可以看出,當位移在2 nm左右時，分子運動加快，大量的金剛石納米顆粒周圍分子被擠入前面吸附層。此時，金剛石納米顆粒與壁面間存在一層潤滑油分子。可以推測如果上下壁面進一步靠近，納米顆粒將會與壁面直接接觸，此時，薄膜就會發生破裂，從而就會發生固體潤滑劑的作用。

2.2 徑向分布函數分析

徑向分布函數(RDF)是描述系統結構特點非常有效的方法，可以表征固體或液體微觀結構的無序化程度[1]。圖4所示為基礎油蓖麻油酸的徑向分布函數。

圖4 基礎油的徑向分布函數(d=4 nm)

圖5表示的是金剛石納米潤滑油分子團的RDF對比，可以發現納米潤滑油與蓖麻油酸基礎油的RDF在2～4 nm之間有些許偏差，當上壁面位移超出這部分范圍時，二者的曲線才逐漸趨于平穩，這說明金剛石納米顆粒周圍稀疏的吸附層對油膜分子排列的緊密程度和邊界條件下潤滑膜強度具有一定的影響，但是影響不大。

當油膜的厚度下降到某一程度后，油膜的各部位厚度就會發生轉變，轉變為“上下壁面吸附層和四周吸附層以及金剛石納米顆粒”，三者之間的彼此作用提高了邊界潤滑膜的強度和承載力。可以看到納米粒子并沒有明顯的變形，只是隨著油液一起向下運動，此時，油液分層現象更加明顯，分層數也有一定的減少，單層油膜厚度也在增加，層數減小。但是，金剛石納米顆粒只能在一定載荷范圍內提高邊界潤滑的承載能力，載荷超過這一范圍時邊界膜將會發生破裂，導致邊界潤滑膜的承載能力失效。

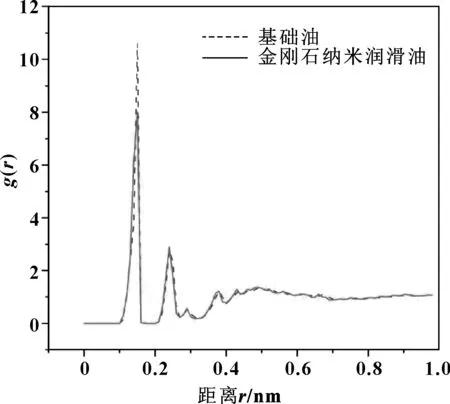
圖5 金剛石納米潤滑油分子團與基礎油液徑向分布函數的對比(d=4 nm)

2.3 納米顆粒的角速度分析

如圖6 所示，改變周期性邊界條件中的顆粒數量和粒徑，使系統內的顆粒體積分數發生變化。當顆粒體積分數一定時，粒徑變小，潤滑膜承載力越高，金剛石顆粒的個數也會增加，納米顆粒對基礎潤滑油的布朗運動效果也會加強，無規則運動也會進一步增強。

圖6 高體積分數的納米顆粒潤滑油分子動力學模型

如圖7—9所示，可以發現，粒徑越小，納米粒子的轉動角速度越高，這個現象進一步說明了納米粒子大小的擾動問題。此外，納米粒子的直徑擴大，增大了粒子體積效應的影響效果。因而，隨著粒徑的減小，納米粒子潤滑膜的承載能力增強，液固轉化的壓力變大，摩擦力降低。

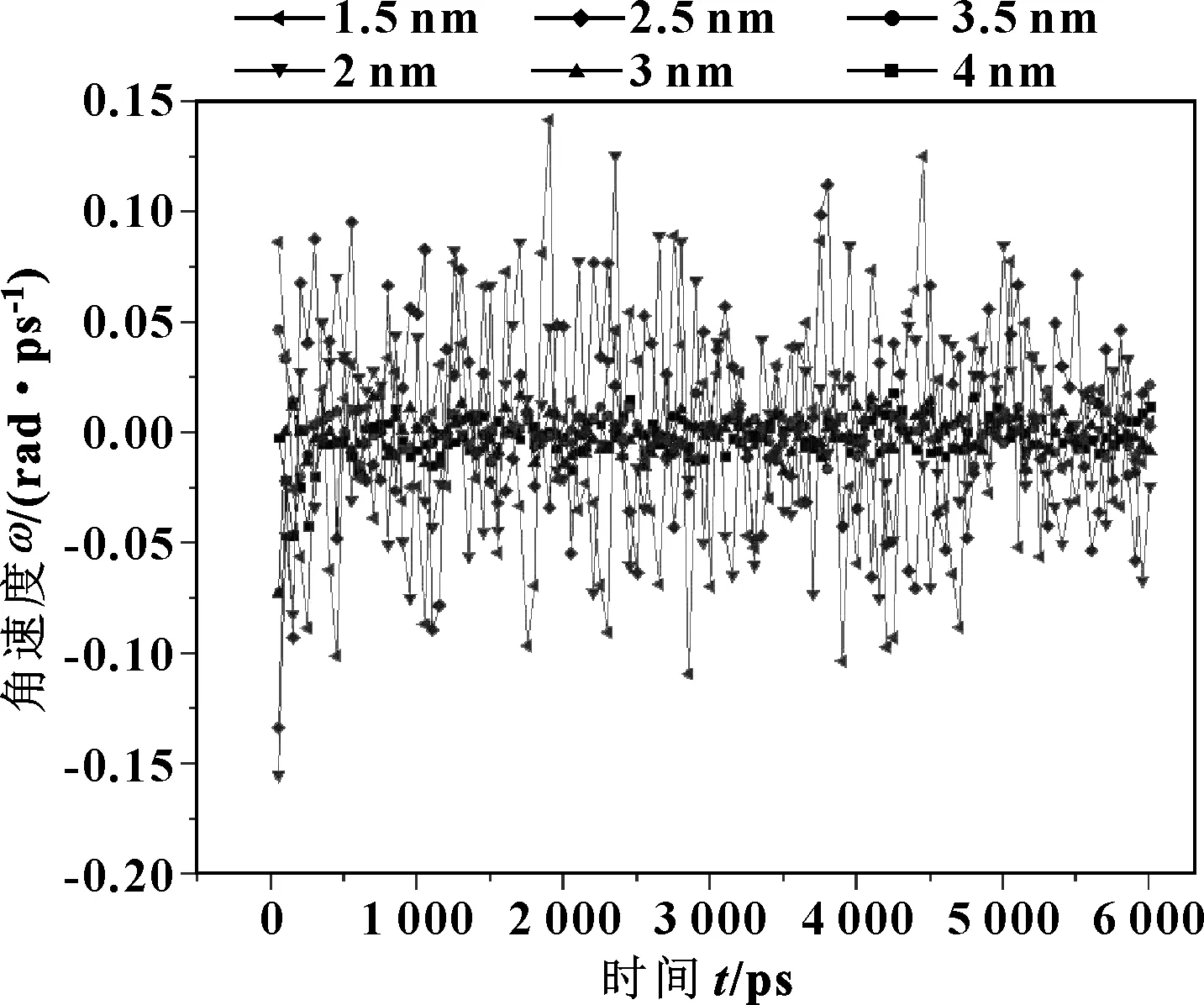
圖7 不同粒徑納米顆粒繞x軸的轉動角速度分量

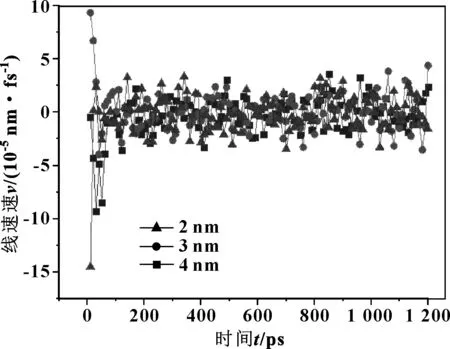
圖8 納米顆粒的線速度

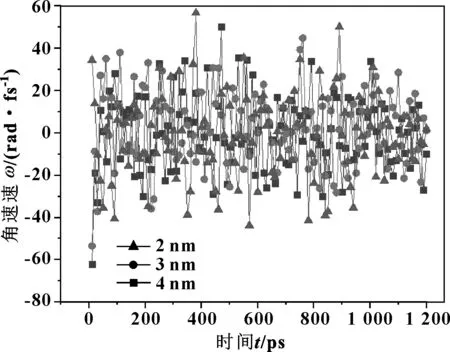
圖9 納米顆粒繞x軸的轉動角速度

2.4 系統的熱導率

根據熱力學第二定律，一個系統在不受外力作用時，若其內部有熱力學性質的不均勻性，則它一定處于非平衡的狀態，并有向平衡態靠近的趨勢。這種由熱力學性質的不均勻性導致的熱力學過程叫做輸運過程。將一個系統置于2個溫度不同的熱源之間，最終會在系統內建立一個穩定的溫度分布。可認為這樣的系統處于一個穩態，但不處于一個平衡態。

如圖10所示為非平衡態熱傳導模擬，在非平衡態熱導率(NEMD)方法中，首先建立一個溫度梯度，并弛豫足夠長的時間，使得系統達到穩態。在達到穩態后，對系統的溫度梯度和非平衡穩態熱流進行測量，然后就可以根據傅里葉定律來計算熱導率。將模擬系統在熱傳導方向分割為若干相等塊，將其中的兩塊分別設置為熱源區域和熱匯區域。采用周期邊界條件，塊的個數一般取為偶數2N，并可以取第1塊為熱源，取第N+ 1塊為熱匯，或者反過來。

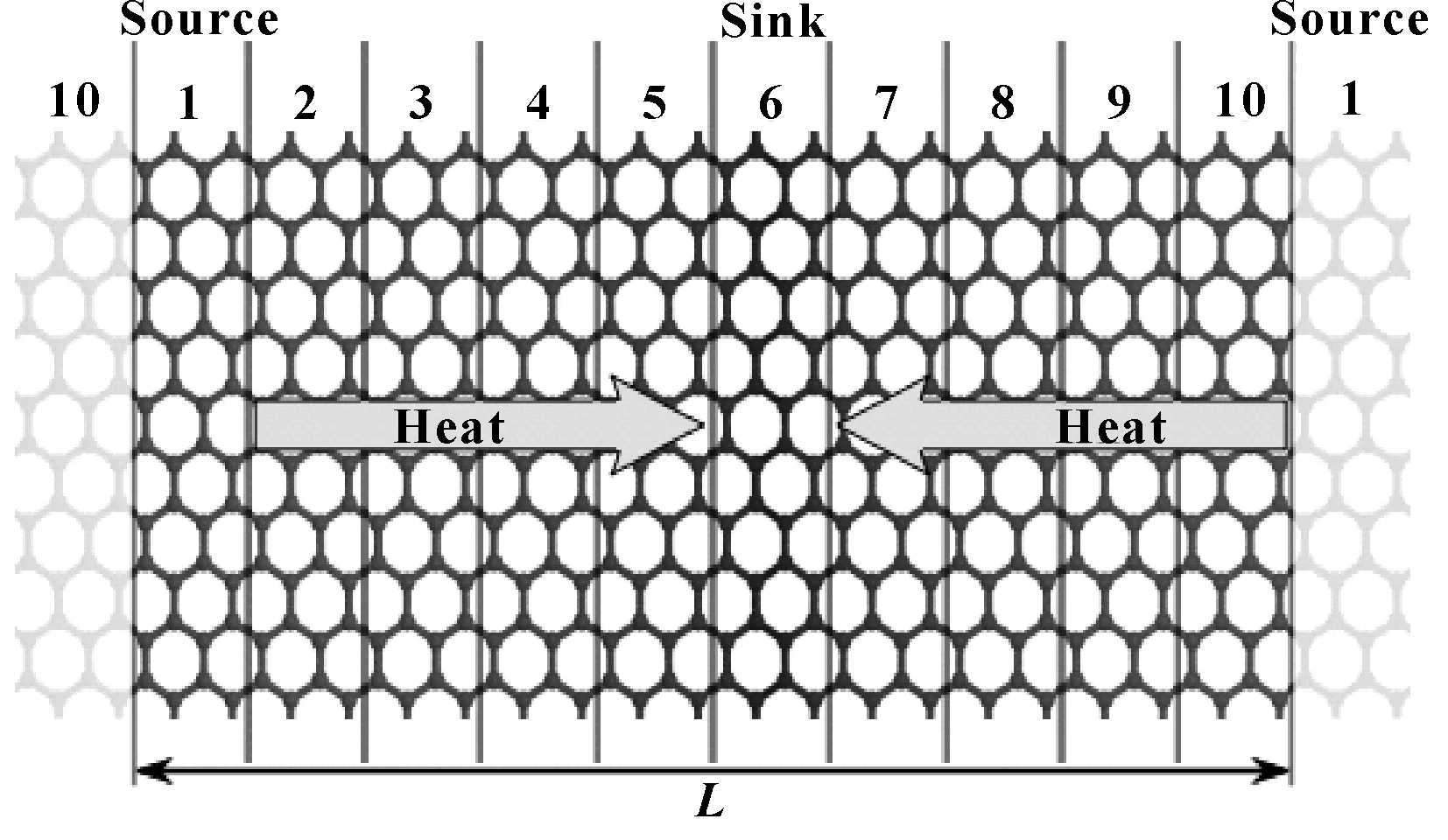
圖10 非平衡態熱傳導模擬

在基礎液油中，導熱系數可以運用導熱儀測得，如DTC-300，僅需比較小的樣品，就可以通過比較小的容器測得，薄膜也可以使用多層技術準確得到測量值。但是在加入納米金剛石顆粒之后，混合油模擬過程中的瞬時熱導率只能通過計算機模擬得到。根據圖11所示的體系溫度分布，在體系的兩側添加熱源并且繪制初始狀態的溫度分布情況。圖12示出了模擬得到的熱導率隨模擬時間點的變化，熱導率會在其準確值上下進行浮動，最后進行數據處理可以得到相對準確的數據。

圖13所示是253 K溫度下，納米顆粒體積分數分別為0、0.6%、1.2%、1.8%和2.4%時潤滑油的熱導率。結果表明，納米粒子體積分數的提高會極大地影響潤滑油的熱傳導，使納米流體的熱導率呈近似線性增加。其主要原因是，納米粒子的傳熱性大于液體分子，并且每一個加入的納米粒子對液體都會有較大的擾動，從而增強了納米流體的熱導率。因此，在保證納米流體液體性質的前提下，適當增大納米粒子體積分數可以有效提高納米流體的熱導率。

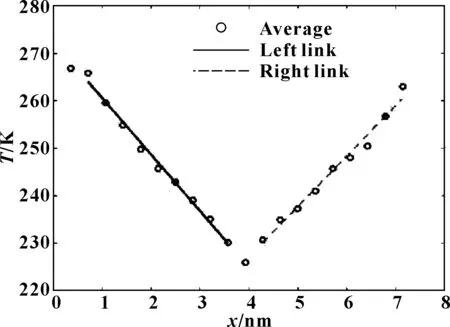
圖11 系統局部溫度熱流

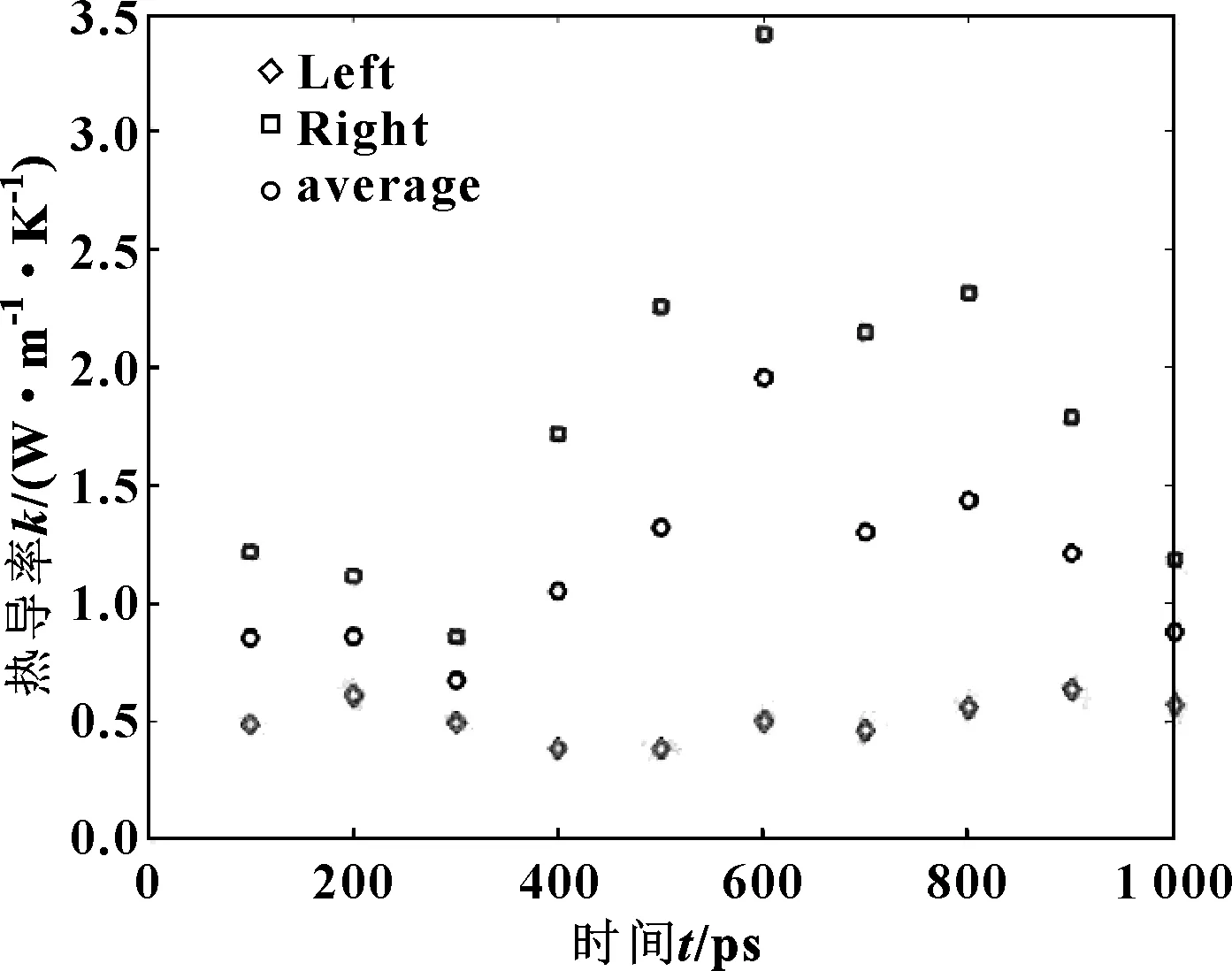
圖12 熱導率隨模擬時間點的變化

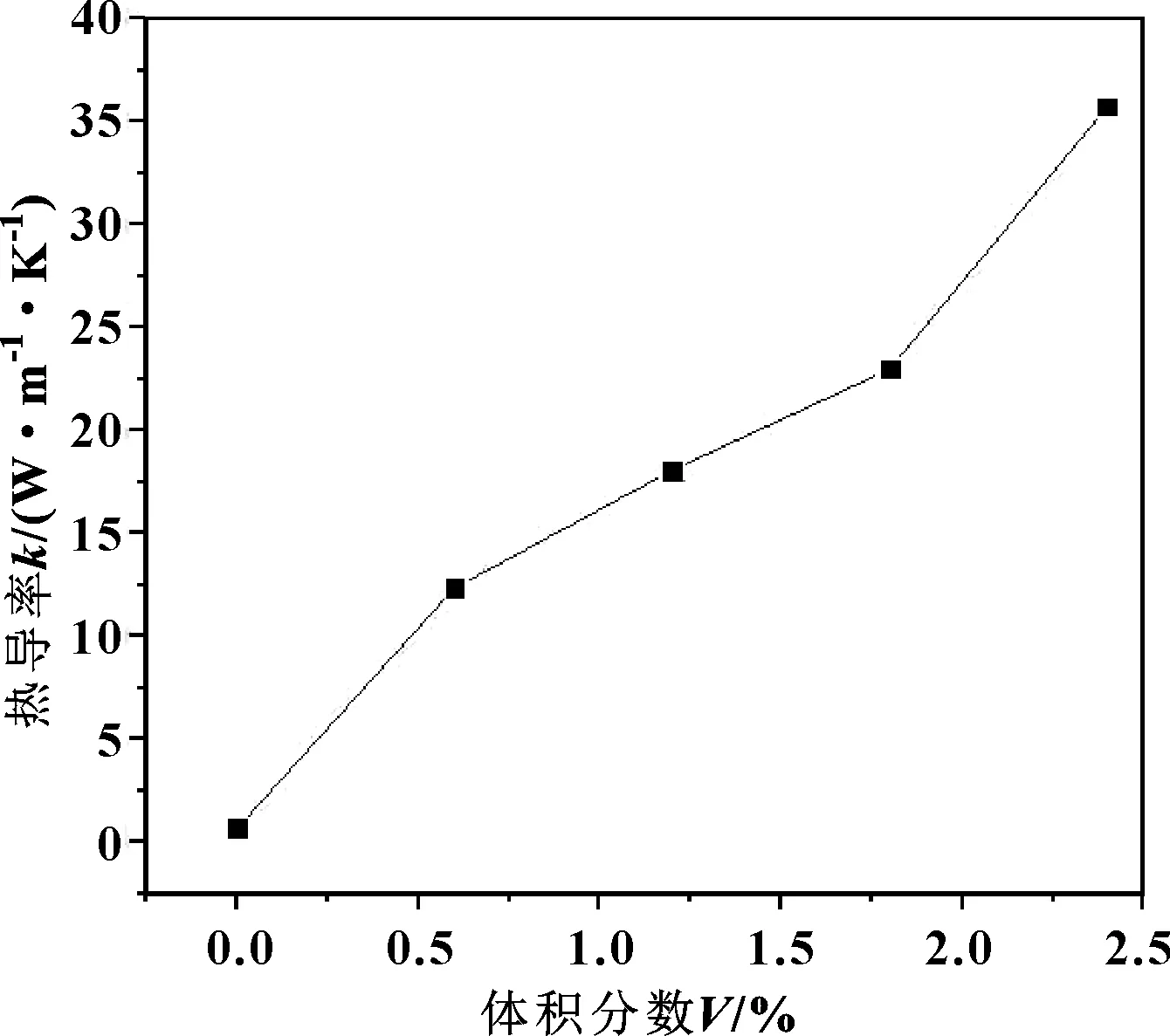
圖13 不同體積分數納米顆粒潤滑油的熱導率

3 結論

(1)納米粒子加入基礎油液中，會與基礎油之間發生吸附作用，在納米粒子表面形成吸附層，當載荷在納米管潤滑膜的可承受范圍內時是可以存在邊界潤滑的。納米粒子在布朗運動的作用下也會產生能量交換，促進納米流體液體間的能量傳遞。因為布朗運動的作用，納米粒子周圍表現出較高的不穩定性。納米流體與基礎流體相比有更好的減摩性能，納米粒子受到的布朗運動更加劇烈，對減摩性能有較大影響。

(2)在形成邊界油膜后，金剛石納米顆粒可以提高基礎油液的承載能力，但是由于壁面和納米顆粒周圍的吸附層在壓縮過程中不斷靠近，納米顆粒在邊界油膜被破壞之前就發生了形變，在此之前，邊界油膜能很好地保護納米顆粒。

(3)當系統中的納米顆粒粒徑發生變化時，在壓縮和滑動過程中，納米顆粒的轉動角速度會發生變化，粒徑越小，轉動速度就越高；反之，轉動速度就越小，相應地摩擦力就會發生變化。

(4)利用非平衡態熱導率的方法研究了納米金剛石潤滑油的熱導率，發現納米顆粒的加入會使得基礎油液熱導率提高，隨納米粒子體積分數的增加，納米流體的熱導率呈近似線性增加。

(5)文中研究方法也可用于其他系統的傳熱研究，在獲得穩定的溫度分布后，通過線性擬合的方法來確定溫度梯度。所有的模擬都在熱傳輸的線性響應范圍內，進一步驗證了傅里葉定律求得NEMD熱導率方法的可行性。在模擬實驗中可以發現，在比較長的樣品模擬中，溫度梯度應該很小，否則靠近熱源的溫度將偏離目標溫度，導致溫度分布非線性。