基于改進R/S估計算法的網絡流量長相關性分析
榮紅佳,盛虎,閆秋婷
(大連交通大學 電氣信息工程學院,遼寧 大連 116028)*
水文專家H.E.Hurst經過長期研究發現水文數據存在長相關性(長記憶性),即某一階段河流流量的數據變化將對以后很長時間的流量數據產生影響.而在此之前的水文數據研究都忽略了水文數據長相關性的存在,從而導致數據模型和流量預測數據不準確[1-2].為了紀念Hurst的發現,使用Hurst指數來描述一個時間序列的長相關性.H.E.Hurst 1951年提出傳統R/S估計算法對Hurst指數進行估計,為隨機信號的長相關特性分析奠定了基礎.Hurst指數估計在股票趨勢分析、網絡流量預警、交通調度、反恐戰備等領域中起著至關重要的作用.而如今大數據時代的來臨,帶來了海量的數據資源,更是為Hurst指數的研究帶來重大的支持.
Hurst指數計算的準確度直接影響著系統模型和預測的準確度,為了提升R/S估計算法的準確性,學者們提出了不同類型的R/S改進算法,對算法性能進行了評價.Mandelbrot B.B.和 Wallis J.R.給出重標極差R/S估計算法魯棒性分析[3];Lo,Andrew W給出一種改進型R/S估計算法,將長相關分析推廣到非高斯信號分析[4];Giraitis L和Kokoszka P等人于2003年給出一種基于V/S統計量的重標度方差估計算法,并分析了算法的可靠性[5].
本文針在對比分析以上研究成果的基礎上,對傳統R/S估計算法中的重新標度方法進行改進和優化,給出一種基于序列長度公約數的改進R/S估計算法,一定程度上提升了算法準確度和計算速度.此外,將算法應用于真實的網絡流量數據長相關特性分析,得到了較好的分析結果.
1 Hurst指數和傳統估計算法及相關對比估計算法介紹
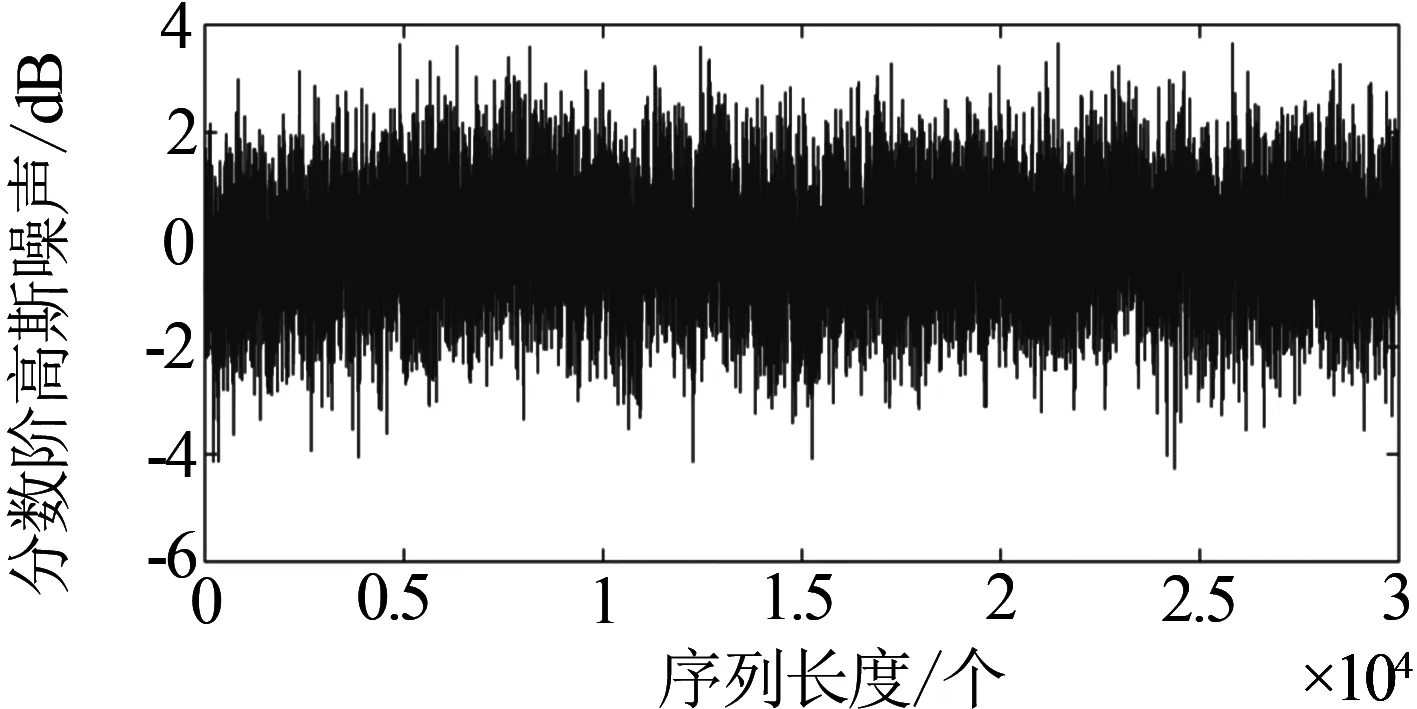
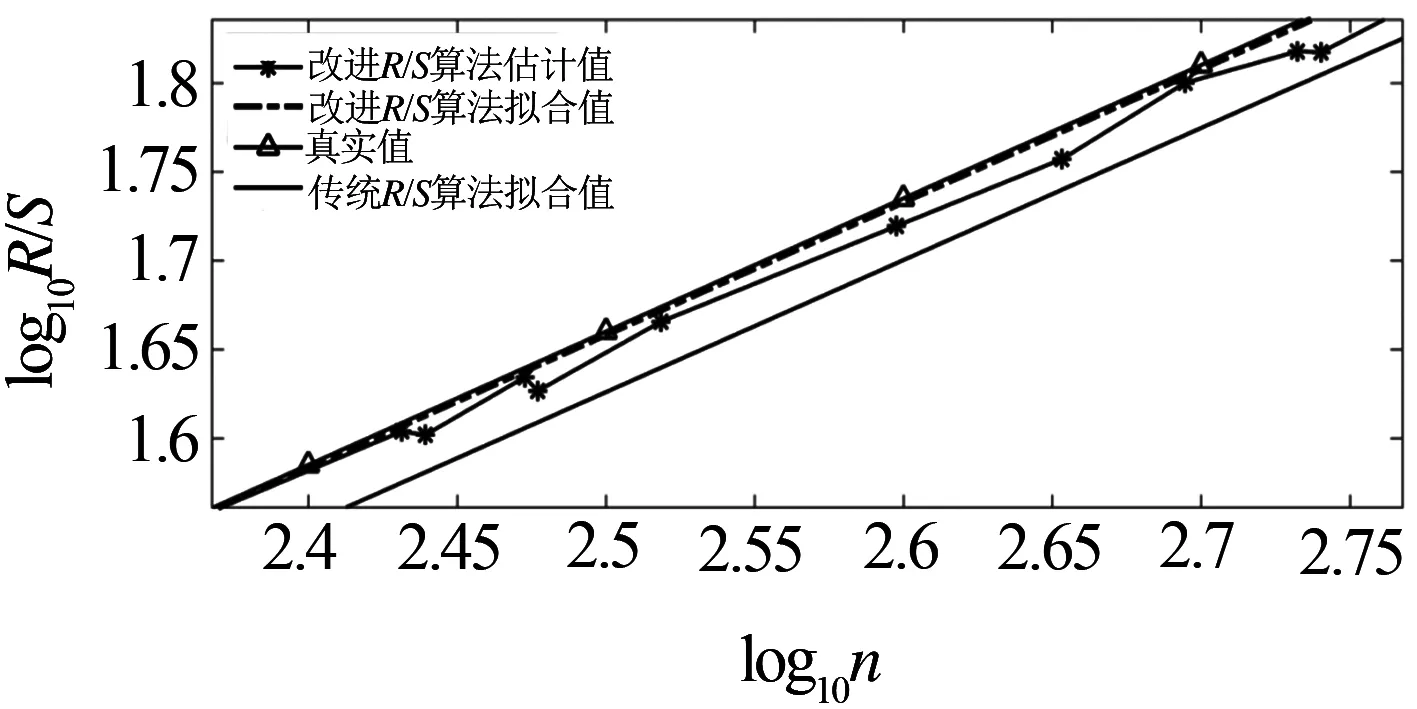
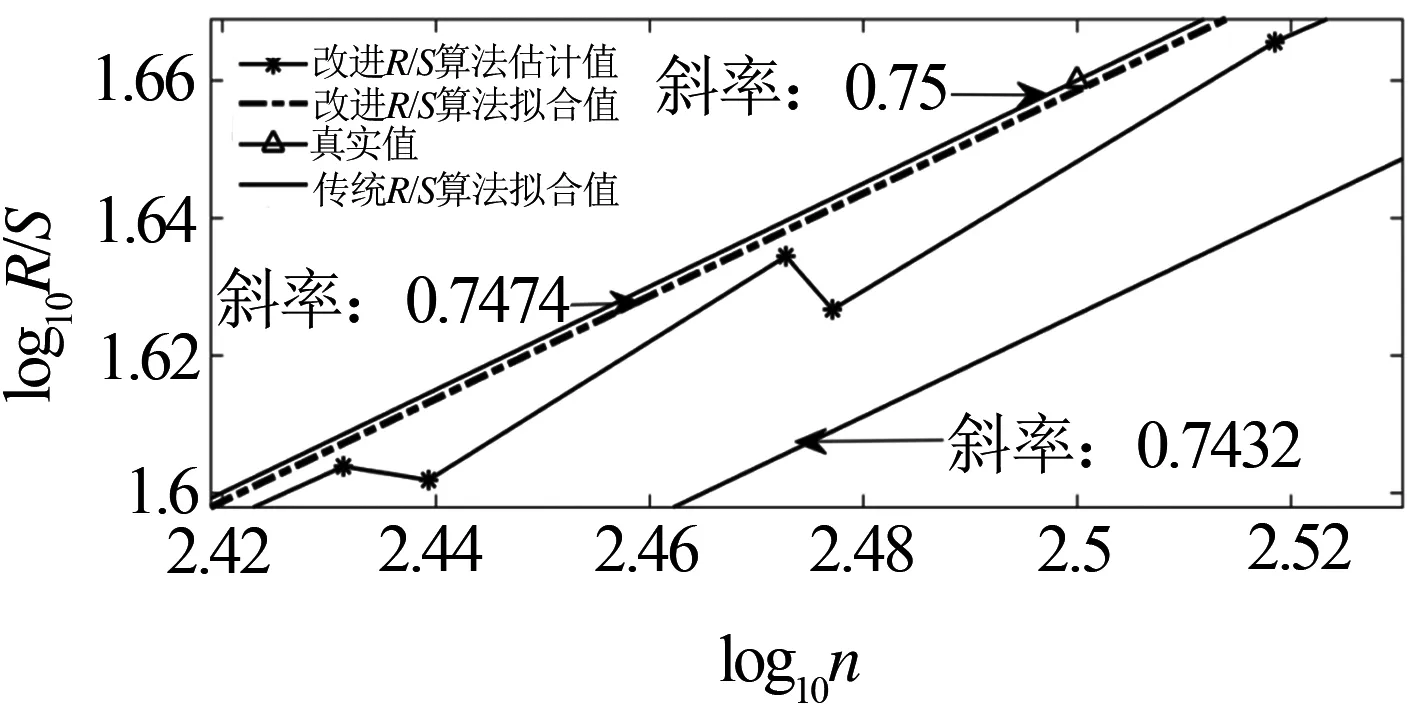
Hurst指數用于測量隨機序列的長相關或長記憶特性,當H=0.5時,時間序列就是標準的隨機游走,可以認為現在時刻對未來不會產生影響,時間序列是沒有記憶性的[6].當0.5 傳統R/S估計算法提供了一個標準化的時間序列統計方法,用于揭示隨機過程中的長期相關性.傳統R/S估計算法是目前為止最常用的Hurst指數估計方法之一,基本思路是研究不同時間尺度條件下時間序列的變化,分為不相關的時間序列和相關的時間序列,研究整體與局部之間自相似性客觀存在的統計特性.傳統R/S估計算法首先將數據分成長度相等且互不重疊的子序列并計算子序列的均值和離差[8-10],進一步計算極差和標準差得到RS值的標準差,估計得到Hurst指數. 具體的,針對長度為n的時間序列x1,x2,…,xn,傳統R/S估計算法的基本步驟如下:首先對序列進行重新標度,重新標度的參考值集合dn={1,2,…,n},即將序列按照集合d中的取值分為n組子序列,每個子序列的長度滿足: (1) 然后再對以上每個子序列進行特定的運算,最后得出Hurst指數的值.從式1中可知,傳統的重新標度方法中參考值的合集取到了從1~n的所有值,或者間隔某一定數量進行取值,兩種方法都未對信息進行刻意篩選,前者導致計算量過大,從而計算效率低,后者幾乎必然會導致信息的丟失,從而導致計算出現偏差. 殘差方差估計算法針對長度為n的時間序列x1,x2,…,xn,將序列分成大小為m的子塊,其中每個子塊的部分和為Y(t),最小均方線為a+bt,然后計算其余數的樣本方差: (2) 該方差正比于m2H,利用log-log圖進行最小二乘擬合,得到擬合直線的斜率為2H,進而可以得到Hurst指數的估計值H. Higuchi估計算法對長度為n的時間序列x1,x2,…,xn,重新構造成一組新的數據: (3) 式中,m,k為整數,分別為初始時間和間隔時間.設定時間間隔為k,則可以構造出k組新的序列.Higuchi法的計算公式如下: (4) 如果給定的序列具有長相關性,那么滿足E(Lm(k))∝CmH-2.利用log-log圖進行最小二乘擬合,得到擬合直線的斜率為H-2,由此可以得到Hurst指數的估計值H. 所以,傳統R/S估計算法中重新標度過程對計算量和準確度影響極大.本文就傳統R/S估計算法中重新標度過程提出改進,在提升計算效率和準確度方面具有實際的意義. 對傳統R/S估計算法進行改進,首先對時間序列進行重新標度,重新標度的合理性直接影響其計算自相似序列Hurst指數的準確度,算法在重新標度的過程中,第一要考慮信息的完整性,當序列的長度與份數不能整除時,會有一部分信息丟失,從而造成計算出現偏差;第二要考慮計算的效率,例如將序列完全離散化或者直接使用整個序列進行計算,導致包含的信息量過大而沒有計算意義. 考慮到以上兩點,本文給出了一種基于序列長度公約數的重新標度方法,在1~n的分組策略中,利用公約數可以被整除的特性,挑選出了基于序列長度公約數的集合,既保證了計算時不會出現信息丟失,保證了估算的準確度,由于避免了一些沒有意義的計算,也一定程度上提高了計算的效率,節省了計算的時間.針對長度為n的時間序列x1,x2,…,xn,算法的基本步驟如下: (1)找到一個略小于序列長度的參考值n′,其滿足n′=μn,μ為一個非常接近1的數,例如μ=0.99,這樣可以保證在重新標度時,不會取到整個序列. (2)找到參考值n′公約數的集合d={d1,d2,…,dk}, (5) 其中,i為整數,由于d為公約數的集合.同時d1,d2,…,dk大小依次遞增,即公約數從小到大進行排列,為了保證序列在重新標度時,每個子序列的長度不至于太小,所以d1大于dmin,dmin是一個大小合適的數,例如取dmin=50. (3)對序列進行重新標度,將序列分為k組子序列,其每個子序列的長度滿足 (6) 其中,dk取自序列長度公約數的集合.得到子序列 (7) (4)計算子序列的均值: j=1,2,…,Ni (8) (5)計算子序列的離差: j=1,2,…,Ni (9) (6)計算累積離差: i=1,2,…,k,j=1,2,…,Ni (10) (7)計算極差: Ri=max(zij)-min(zij), i=1,2,…,k,j=1,2,…,Ni (11) (8)計算標準差: i=1,2,…,k,j=1,2,…,Ni (12) (9)計算RS值: (13) (10)將計算出的各子序列的RS值求平均: (14) 并計算其標準差: (15) 為了分析基于序列長度公約數的改進R/S估計算法的準確性和計算速度,首先采用功率譜快速傅里葉變換方法合成分數階高斯噪聲(FGN:Fractional Gaussian Noise).該合成方法的原理是利用譜合成法構造一定參數的分數階布朗運動的功率譜密度函數,對功率譜密度函數進行傅里葉逆變換得到分數階布朗運動隨機序列,經過一階差分便可得到FGN隨機序列[11-12].再設定合適的H參數就可以進行FGN的仿真過程.仿真合成Hurst指數分別為0.85、0.8和0.75的長度為30 000的FGN序列,圖1給出了H=0.75的FGN序列. 圖1 H=0.75的FGN序列 使用改進后的R/S估計算法,對相應H值的FGN序列擬合后的結果如圖2所示.其中,星形折線為應用改進后R/S估計算法計算的Hurst值,實線為傳統R/S估計算法擬合值,三角折線為Hurst指數為0.75的真實值,點劃線為多項式擬合后的Hurst指數估計值,代表了Hurst指數的趨勢. 圖2給出了改進R/S估計算法和傳統R/S估計算法計算H=0.75的FGN序列的對比圖,圖3將圖2中局部區域進行放大,并對直線斜率值進行了標注,對比上圖中直線的斜率,可以看出點劃線代表的改進R/S估計算法的斜率值更接近三角折線代表的真實值斜率,計算誤差也較傳統R/S估計算法小,當計算H=0.8和0.85時的FGN序列也可以得出同樣的結論. 圖2 改進R/S估計算法對H=0.75FGN序列的擬合 圖3 改進R/S估計算法對H=0.75FGN序列的擬合局部放大圖 表1 本文方法傳統Hurst估計算法準確度和計算速度對比 針對長度為30000Hurst指數分別為0.75、0.8和0.85的FGN序列,采用傳統R/S估計算法、改進R/S估計算法、殘差方差估計算法、Higuchi估計算法進行估計并記錄估計值和計算速度.表1給出了四種算法在Intel(R) Core(TM) i5-8250處理器,8G內存,MATLAB2016b版本計算機運行得到的估計值和計算耗時數據,對比數據可以看出在準確度方面: 改進R/S估計算法計相比其余三種估計算法的準確度更高;在計算耗時方面:四種方法耗時從小到大分別為:Higuchi估計算法、殘差方差估計算法、改進R/S估計算法、傳統R/S估計算法,改進R/S估計算法雖然速度并不是最快,但是相比傳統R/S估計算法計算速度提升較大. Hurst指數作為自相似性網絡流量的重要指標,對網絡流量數據長相關特性的定量研究已成為網絡流量特性研究的重點內容,如何快速、有效地估計Hurst指數對于網絡流量相關業務的應用具有重要的意義[13-15].為了驗證前面所介紹的基于序列長度公約數分段的改進R/S估計算法的有效性,本文采用美國貝爾實驗室名為BC-Oct89Ext.TL的網絡流量數據結合改進R/S估計算法對自相似性網絡流量進行分析和研究.從實際網絡流量分別獲取五段長度為30000的數據,得到五份原始樣本數據并展示其中一份數據樣本如圖4所示. 圖4 網絡流量樣本數據 利用改進R/S估計算法計算五段網絡流量樣本數據的Hurst指數,得到的結果如表2所示. 表2 網絡流量樣本數據Hurst值 從表2可知,應用改進R/S估計算法計算的Hurst指數值介于0.5~1之間,說明網絡流量數據具有長期相關性,即該序列具有正的持續性,而且H值雖然在0.5~1之間但更偏向1,H值越大,說明這種正持續性越強.并且隨著H值的增大,網絡流量數據具有的長相關性變強.應用傳統R/S估計算法在計算數據Ⅲ和Ⅴ的Hurst指數值時;應用殘差方差估計算法在計算數據Ⅴ的Hurst指數值時;應用傳統R/S估計算法在計算數據Ⅲ和Ⅴ的Hurst指數值時;應用Higuchi估計算法在計算數據Ⅱ的Hurst指數值時出現了大于1的情況,無法刻畫網絡流量數據的長相關特性,計算結果沒有意義,因此就準確性和有效性來說,改進R/S估計算法計算結果更精準,因此采用改進R/S估計算法計算得出的Hurst指數值在刻畫網絡流量數據長相關特性方面顯得尤為重要. 本文在計算準確度以及計算速度方面將改進R/S估計算法和傳統R/S估計算法、殘差方差估計算法、Higuchi估計算法進行對比,從表1中可以看出,改進R/S估計算法對H值不同的FGN序列估計結果相比傳統R/S估計算法的計算結果更加準確,計算耗時更少,同時改進R/S估計算法相比殘差方差估計算法、Higuchi估計算法,其計算結果也更加準確.對傳統R/S估計算法進行重新標度是計算自相似序列Hurst指數的一個有力工具,消除了傳統R/S估計法中存在的短期依賴性,擴大了長相關序列適用范圍.此外,通過對比H值分別為0.75、0.8、0.85時,傳統R/S估計算法和改進R/S估計算法計算自相似序列Hurst指數的計算速度分別提升了9.76倍、10.25倍、10.48倍,極大的提升了計算效率.由此可見,利用公約數分段法對比傳統R/S估計算法中隨機分段法,由于省去了算法內部一些無意義的計算,所以在計算速度上要上升一個檔次,在有限的時間內運用改進R/S估計算法計算自相似序列的Hurst指數極大的縮短了運算時間,提高了后續的計算效率. 表2給出了五段網絡流量樣本數據經過改進R/S估計算法和傳統R/S估計算法計算得出的Hurst指數值,對比了兩種方法,發現無論在準確性還是有效性方面,改進R/S估計算法都優于傳統R/S估計算法. 傳統的R/S估計算法在重新標度方法上存在欠缺,當序列的長度與分段數不能整除時,會有一部分信息丟失,從而造成計算出現偏差,而且傳統R/S估計算法在計算長相關序列Hurst指數時效率偏低,無法體現與其他方法在計算序列H值的優勢所在.采用公約數分段法對傳統R/S估計算法進行重新標度,可以在準確度和效率方面帶來明顯提升.改進R/S估計算法在網絡流量數據分析結果驗證了算法的有效性,對網絡流量數據長相關性分析提供了一種有效方法.2 基于序列長度公約數的改進R/S估計算法
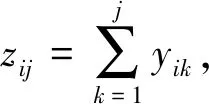
3 基于序列長度公約數的改進R/S估計算法仿真分析
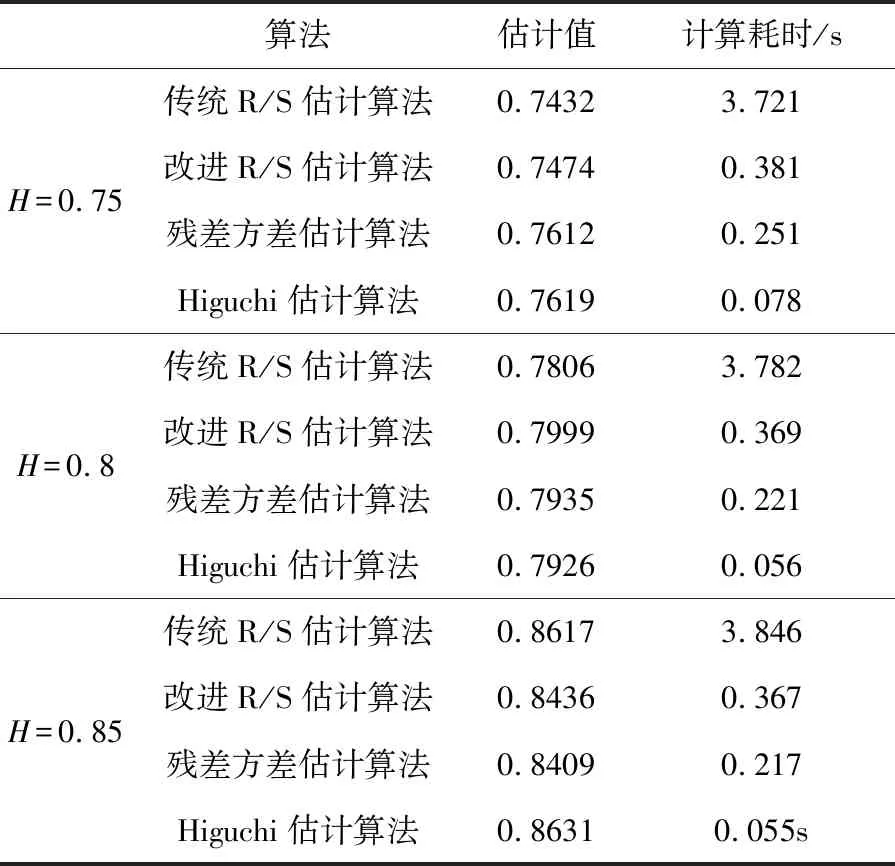
4 改進R/S估計算法在網絡流量數據分析中的應用
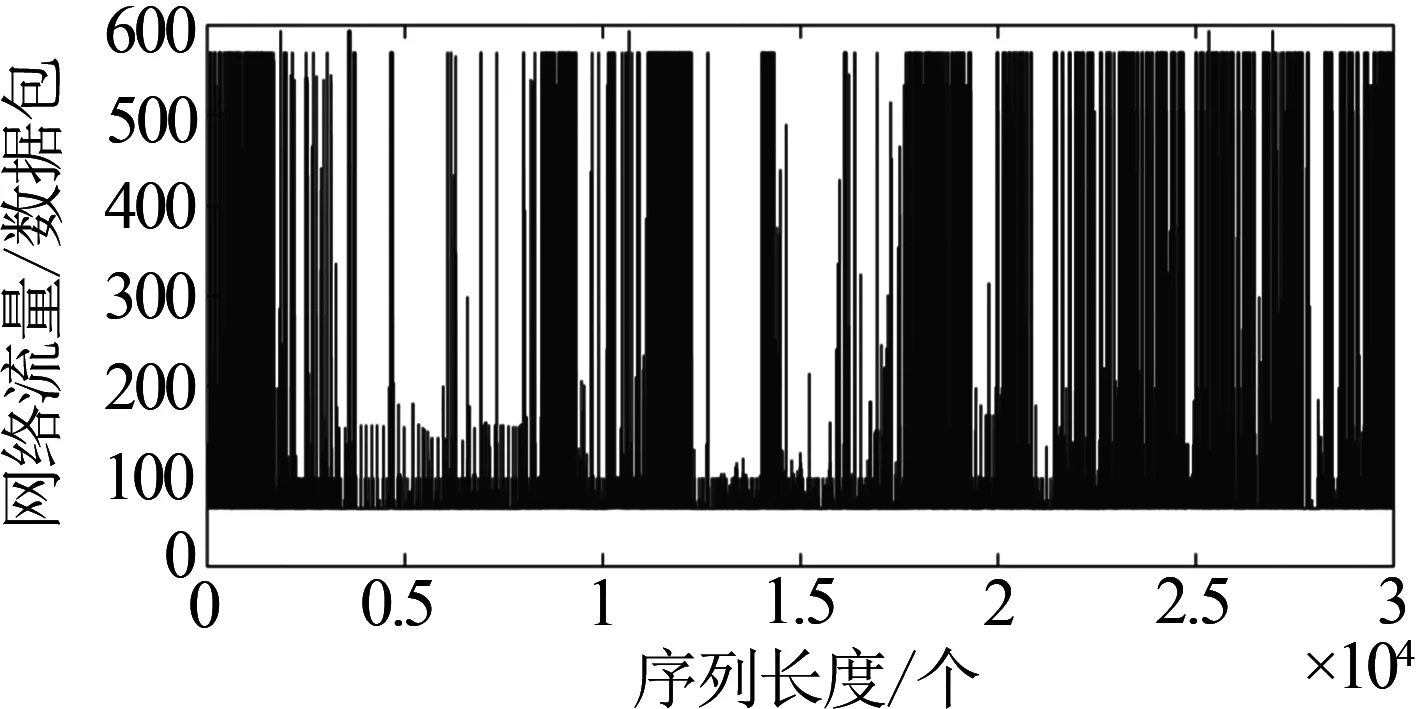
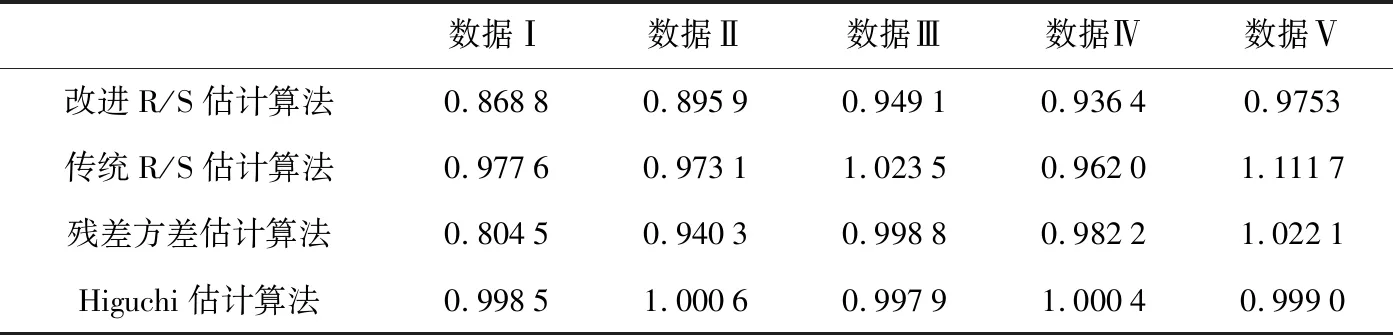
5 結果分析
6 結論

