基于一種條件熵距離懲罰的生成式對抗網絡*

譚宏衛 ,王國棟 ,周林勇 ,張自力,3

1(西南大學 計算機與信息科學學院,重慶 400715)

2(貴州財經大學 數統學院,貴州 貴陽 550025)

3(School of Information Technology,Deakin University,Locked Bag 20000,Geelong,VIC 3220,Australia)

GANs 是由Goodfellow 等人[1]受博弈論中二人零和博弈思想的啟發所提出的一種深度生成模型,其網絡結構主要由判別器網絡和生成器網絡所構成.判別器的目的是盡量正確地判斷:輸入數據是來自真實數據分布還是來自生成分布;而生成器的目的是盡量去學習與真實數據分布一致的分布,并生成以假亂真的樣本.雖然GANs 已廣泛應用于圖像生成[2,3]、超分辨率圖像合成[4,5]、語義分割[6,7]等多個領域,但要生成高質量的樣本仍是該領域的一個挑戰.

為了提高GANs 生成樣本的質量,出現了很多有針對性的算法[8],這些算法主要基于以下兩個角度而提出.

一是基于網絡結構的算法研究.由于GANs 網絡結構的靈活性,其判別器網絡和生成器網絡可以是任何類型的網絡結構.深度生成式對抗卷積網絡(deep convolutional generative adversarial network,簡稱DCGAN)[2]就是其中一種典型的網絡結構算法,其判別器和生成器均使用卷積神經網絡(CNN),同時改變梯度優化算法(Adam)[9],以及加入批量標準化(batch normalization,簡稱BN)[10]層等策略,以提升GANs 網絡的穩定性及整體性能.此后,研究者們將一些高性能網絡模塊嵌入到DCGAN 的網絡結構中,極大地提升了GANs 網絡的性能,如將殘差模塊[11]整合到WGAN-GP[12]中以生成文本,將自注意機制模塊[13]整合到條件GANs 中以生成圖像[14],將Laplacian 金字塔模塊[5]融入到GANs 網絡中以提高人臉圖像生成的質量[4]等.除此之外,還有部分算法是針對特定的應用而提出不同結構的GANs 算法,如SGAN[15]、TripleGAN[16]、CycleGAN[17]、BigGAN[6]等.這些算法基本上都是從純網絡結構角度來設計的,并未考慮樣本多樣性問題.本文利用信息熵來衡量樣本多樣性,并將其融入到算法中以提高GANs 生成樣本的質量.

二是基于目標函數的算法研究.這類算法主要從兩個方面展開研究:(1) 改變目標函數的形式;(2) 懲罰目標函數.針對前者,Nowozin 等人[18]將原始GANs 中的JS 散度[19]推廣到一般化的f 型散度,并提出f-GAN 算法;進一步地,Mao 等人[3]根據原始GANs 的對抗規則,用平方損失函數來代替GANs 中的熵損失函數,從而提出LSGAN 算法.除此之外,Arjovsky 等人[20]從微分流形的角度嚴格證明了JS 散度是導致GANs 生成器梯度消失及訓練不穩定的主要原因,由此他們提出用Wasserstein I 型距離[21]代替JS 散度來衡量真實分布與生成分布之間的距離,并提出WGAN 算法[22].至于后者,Gulrajani 等人[12]利用1 中心梯度懲罰技術來解決WGAN 中Lipschitz 條件的限制,并提出WGAN-GP 算法以提高WGAN 生成樣本的質量.由此研究路線,Hoang 等人[23]開發了零中心梯度懲罰的GANs 算法(GAN-0GP).Miyato 等人[24]提出譜標準化的生成式對抗網絡(SNGAN),他們利用標準化的譜范數來限制判別器網絡的Lipschitz 常數,使得網絡的Lipschitz 常數逼近于1,這相當于對判別器網絡實施正則化.截止目前,雖然有很多優秀的GANs 算法極大地提升了生成樣本的質量,但仍不能滿足現實任務的需求,亟需探索高性能的算法以提高GANs 生成樣本的質量.

基于對上述GANs 算法研究的調查,本文提出一種條件熵距離懲罰的生成式對抗網絡,旨在進一步提高GANs 生成樣本的質量.我們所提出的這一對抗網絡與其他懲罰技術最大的區別在于:懲罰函數直接懲罰生成器,而非判別器.首先,利用條件熵構造一種距離,可證此距離滿足度量空間中的三大條件:正定性、對稱性及三角不等式.為了既能保證生成數據多樣性與真實數據多樣性的一致性,又能迫使生成分布盡可能地逼近真實分布,本文直接用這個距離來懲罰GANs 生成器.除此之外,本文在DCGAN[2]網絡結構的基礎上,進一步優化GANs網絡結構及初始化策略,主要的優化策略有:(1) 將批量標準化(BN)和譜標準化(SN)有機地融入到判別器網絡中;(2) 刪除生成器中的尺度不變層(311 層),即卷積核為3、步長為1 以及加邊數為1 的卷積層;(3) 改變兩個網絡的初始化策略,判別器和生成器均使用正交初始化[25].這樣的網絡結構設計及初始化策略,不但能縮小網絡的參數空間和降低顯存消耗,而且還能提高網絡的訓練效率和性能.

本文第1 節簡要介紹GANs 基礎知識.第2 節構建一種距離,優化網絡結構,并提出一種GANs 懲罰算法.第3 節是實驗.第4 節為本文總結.

1 背景知識

GANs 是一種有效而直接的深度生成模型,其基本網絡結構由判別器網絡D和生成器網絡G所構成.本質上,GANs 的優化問題是一個極小極大問題[1],其損失函數分為兩部分,分別對應于判別器網絡和生成器網絡的損失函數,其損失函數分別如下:

其中,pdata和pz分別表示真實數據分布和隱分布(先驗分布).為便于表示,令表示生成分布,則有從理論上講,GANs 經過多輪迭代,可使生成分布無限逼近真實分布[1].但在訓練之初,方程(2)中的損失函數有可能達到飽和,無法傳遞有價值的信息,使得兩個分布無法逼近.鑒于此,Goodfellow 等人[1]建議將飽和的損失函數(2)轉化成非飽和損失函數,于是有

相比方程(2),方程(3)中的損失函數更能使GANs 訓練穩定,也因此有研究者將原始GANs[1]稱為非飽和型GANs(non-saturating GANs,簡稱NSGANs)[26].

GANs 的訓練過程分為兩個階段:第1 階段訓練判別器D,第2 階段訓練生成器G.當訓練完判別器D之后,傳遞真假信息給生成器G,而生成器G根據信息(實質上是梯度信息)的真偽,調整更新策略,盡量生成高質量的樣本去“哄騙”判別器.于是,產生了這樣的對抗策略:當訓練判別器D時,盡量使D(G(z))=0;而當訓練生成器G時,盡量使D(G(z))=1.通過這樣的對抗策略,判別器和生成器都在不斷地提升彼此的判別能力和生成能力,直到判別器無法判斷生成器生成的樣本是來源于真實數分布還是生成分布.圖1 所示為GANs 的訓練框架圖.

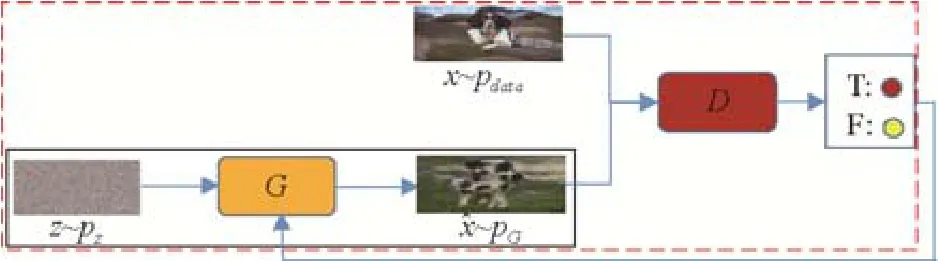
Fig.1 The framework for training GANs:Training D in first stage (in the red dotted box)and training G in second stage (in the black solid line box)圖1 GANs 的訓練框架:第1 階段訓練判別器D(紅虛線框內),第2 階段訓練生成器G(黑實線框內)

2 條件熵距離懲罰的生成式對抗網絡

本節將詳細闡述本文所提出的懲罰算法.首先,利用條件熵構建一種距離,并將其直接懲罰于生成器的非飽和損失函數上,即方程(3);其次,在DCGAN 網絡結構[2]的基礎上,優化GANs 的網絡結構及超參設置,改變生成器網絡和判別器網絡的初始化策略,以此來提升模型的訓練效率及性能.

2.1 條件熵距離

信息熵是隨機變量不確定程度的度量;它也是從平均意義上描述隨機變量所需信息量的度量.設X是離散型隨機變量,其分布函數為則X的信息熵[19]為

其中,x 表示隨機變量X的取值空間.同理,對于離散型隨機變量Y,有其中,FY(y)是隨機變量Y的分布函數,y 是Y的取值空間.對于在X給定的條件下,隨機變量Y的條件熵[19]可定義為

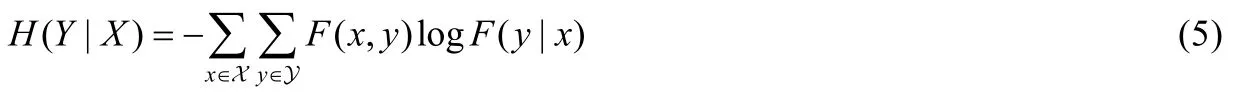
其中,F(x,y) 和F(y|x) 分別表示X和Y的聯合分布函數和條件分布函數.若要度量兩個隨機變量分布之間的距離,可用它們之間的KL 散度[19]來度量,其定義如下:

現考慮度量兩個隨機變量X和Y之間的關系或一個隨機變量包含另一個隨機變量的信息量,可用兩個隨機變量之間的互信息來度量[19],其定義為

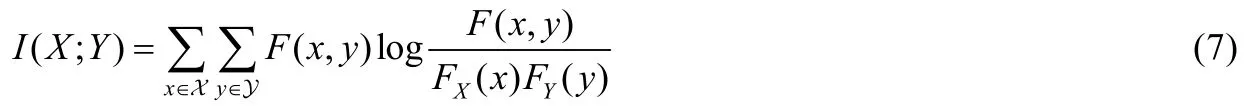
由KL 散度(6)定義可知,I(X;Y)=D(F(x,y)||FX(x)FY(y)).由此可見,I(X;Y)也度量了兩個隨機變量之間的距離;同樣,I(X;Y)非負,并且,當且僅當X=Y時,I(X;Y)=0.但是,I(X;Y)同樣不是兩個隨機變量之間真正的距離,因為它不滿足距離定義中的三角不等式.鑒于此,根據方程(5)可構造如下距離:

而又由I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X),可得ρ(X,Y)=H(X)+H(Y) -2I(X,Y).由方程(8)可知,ρ(X,Y)由條件熵所構成,故稱其為條件熵距離(conditional entropy distance,簡稱CED).需要特別指出的是,若X和Y為連續性隨機變量,只需將每個定義中的分布函數換成概率密度函數,求和符號換成相應的積分符號即可.

定理1.ρ(X,Y)是一種距離,即滿足:

(1) 正定性:ρ(X,Y) ≥ 0,當其僅當X=Y時,ρ(X,Y)=0.

(2) 對稱性:ρ(X,Y)=ρ(Y,X).

(3) 三角不等式:對于隨機變量X、Y、Z,有ρ(X,Y)+ρ(Y,Z)≥ρ(X,Z).

證明:

(1) 正定性.由于熵是非負,得ρ(X,Y)=H(X|Y)+H(Y|X) ≥ 0,并且當X=Y時,H(X|Y)=H(Y|X)=0,可知ρ(X,Y)=0;反之,當ρ(X,Y)=0時,由ρ(X,Y)=H(X|Y)+H(Y|X)及熵的非負性,有H(X|Y)=H(Y|X)=0,此時X=Y.因此,ρ(X,Y) ≥ 0,當其僅當X=Y時,ρ(X,Y)=0.

(2) 對稱性.由ρ(X,Y)=H(X|Y)+H(Y|X)=H(Y|X)+H(X|Y)=ρ(Y,X)易知,ρ(X,Y)=ρ(Y,X).

(3) 三角不等式.若要證ρ(X,Y)+ρ(Y,Z)≥ρ(X,Z),只需證H(X|Y)+H(Y|X)+H(Y|Z)+H(Z|Y)≥H(X|Z)+H(Z|X)成立.而對于隨機變量X、Y、Z,有H(X|Y)+H(Y|Z)≥H(X|Y,Z)+H(Y|Z)=H(X,Y|Z)=H(X|Z)+H(Y|X,Z)≥H(X|Z).

同理可得,H(Y|X)+H(Z|Y)≥H(Z|X),合并兩個不等式就有H(X|Y)+H(Y|X)+H(Y|Z)+H(Z|Y)≥H(X|Z)+H(Z|X)成立,即有ρ(X,Y)+ρ(Y,Z)≥ρ(X,Z)成立.因此,ρ(X,Y)是一種距離.證畢.□

2.2 生成器的條件熵距離懲罰

GANs 生成樣本的質量與其樣本的多樣性和逼真度密切相關.鑒于此,需構建這樣一種GANs 算法:在保持多樣性的同時,盡量使得生成分布無限逼近真實分布.利用條件熵距離能實現這樣的算法,信息熵可度量樣本的多樣性,而由此構造的距離可度量生成分布與真實分布之間的距離.為此,只需將條件熵距離直接懲罰于GANs生成器的目標函數上,使之生成的樣本更具多樣性和高逼真度,從而提高GANs 生成樣本的質量.在判別器損失函數不變的條件下,將條件熵距離直接加入到生成器非飽和損失函數中,即方程(3)中,有:

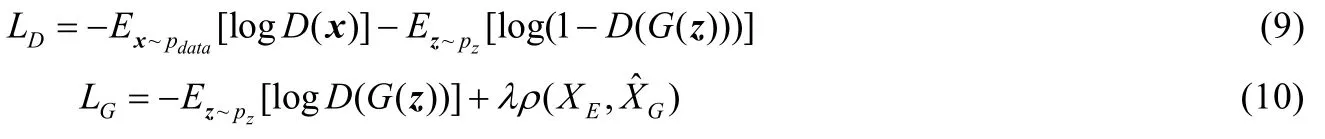
其中,λ是懲罰因子.在實際中,并不容易估算方程(10)中的條件熵距離,其需要具體的分布函數或密度函數表達式,以圖像生成為例,圖像數據的真實分布和生成分布并不可知.在這種情況下,用經驗分布函數代替真實分布函數不失為一個好的選擇.設真實數據樣本的經驗分布函數為pEdata,生成數據樣本的經驗分布函數為pEG,則方程(10)中的由此看出,隨機變量的取值空間分別是真實數據域和生成數據域.由損失函數方程(9)和方程(10)構成的GANs,我們稱其為條件熵距離懲罰的GANs,簡記為熵距離GANs(entropy distance GAN,簡稱EDGAN).EDGAN 的算法流程如算法1 所示.

算法1.條件熵距離懲罰GANs 算法(EDGAN).

EDGAN 算法利用小批量隨機梯度下降法訓練網絡,同時使用OAdam 梯度優化算法(β1=0.5,β2=0.9),判別器和生成器均使用正交初始化,懲罰因子λ設為1.

輸入:

· 樣本批量數m=64;

· 兩個網絡學習率:判別器lr_D=0.0001,生成器lr_G=0.0004;

· 隱分布Z～N128(0,0.02);

· 網絡迭代總次數k= 100000;

· 判別器迭代次數kD=2,生成器迭代次數kG=1.

根據條件熵距離的特性,EDGAN 算法在盡量保持樣本多樣性的同時,使得生成分布與真實分布之間的距離盡可能地接近,即在EDGAN 算法的更新過程中,同時考慮樣本的多樣性和逼真度兩個因素,這有助于提高GANs 生成樣本的質量.雖然GANs 的目標函數是影響其性能的關鍵因素,但絕不是唯一的影響因素,這其中還有網絡結構、超參設置及初始化策略等因素都有可能影響其性能.因此,優化GANs 的網絡結構及參數設置也是提升GANs 性能的重要技術手段之一.本文將在DCGAN 網絡結構[2]的基礎上,優化GANs 的網絡結構及超參設置,改變GANs 的初始化策略,縮小GANs 的參數空間,加速GANs 的訓練效率,并結合懲罰機制,提升GANs的整體性能.

2.3 優化網絡結構

DCGAN 的網絡結構是一種經典的GANs 網絡結構,其判別器網絡和生成器網絡均使用卷積神經網絡(CNN),它的基本參數設置是:在判別器和生成器中均使用批量標準化(BN),生成器的激活函數除輸出層用Tanh函數外,其余層都使用ReLU 激活函數[27],判別器除最后一層用Sigmoid 激活函數外,其余層均使用LeaklyRelU激活函數[28](斜率為0.2),兩個網絡的參數初始化都取值于N(0,0.02)隨機數,兩個網絡的學習率都是0.000 2,隱分布是均勻分布U[-1,1],批量數(batchsize)是128,梯度優化算法是Aadm 算法[9](β1=0.5,β2=0.999).圖2 是圖像尺寸為3 × 32 ×32 的DCGAN 網絡結構,其中,在判別器中類似于conv 64 3 1 1 BN LReLU 的卷積層依次表示該卷積層網絡的輸出通道是64(即深度),卷積核(kernel)是3,步長(stride)是1,加邊數(padding)是1,卷積操作之后執行批量標準化,最后使用激活函數LReLU(LeakyLReLU)輸出該層網絡結果.同理,在生成器中,首先將隱分布隨機數(noise)壓縮成尺寸為512 × 4 ×4 的樣本,然后傳入下一層;deconv 表示降卷積網絡層,其他表示的含義與判別器一樣.

本文所有的實驗都在Pytorch 框架[29]下完成,為了便于表示和敘述,其網絡結構的表示方法也是借助于Pytorch 中的表示方法.在Pytorch 中,如果卷積核為3,步長是1,加邊數也是1,則無論是判別器中的卷積層還是生成器中的降卷積層的輸出尺寸與上一層的尺寸一致,我們將這種卷積層稱為311 尺度不變層.這種卷積層具有特殊的含義,它只提取特征不作尺度變換.因此,在DCGAN 的網絡結構中,常在311 尺度不變層后面加上尺度變換層構成另一類輸出通道下的樣本尺度.這樣的設計在每類輸出通道下都要進行兩次特征提取,使得所提取的特征更加精細化.如果在判別器中精細化的特征更有利于提升其判別能力,但在生成器中,就不一定能夠提升生成能力.因為精細化的特征使得生成器更容易忽視樣本的一般特征,從而導致生成的樣本質量反而下降.后面的實驗也證實了這樣的判斷.

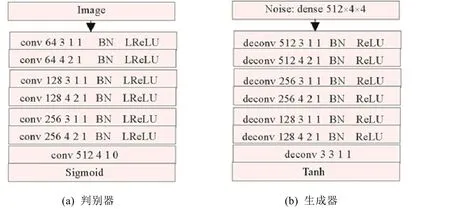
Fig.2 The 3 × 32 × 32 network structure of DCGAN圖2 圖像尺寸3 × 32 × 32為的DCGAN 網絡結構

優化網絡結構是提升GANs 性能的技術之一.鑒于上述分析,剔除DCGAN 生成器中所有的311 尺度不變層將有助于提升GANs 生成樣本的質量,同時也極大地縮小生成器網絡的參數空間,加速網絡的訓練效率.特別需要強調的是,圖2 所示生成器的倒數第2 層也是311 層,但其真正的目的是通道變換,而非特征提取,所以不能剔除.除此之外,本文還將SNGAN[24]中的譜標準化(SN)策略融入到GANs 的判別器中.與DCGAN 和SNGAN最大的不同是,改進的判別器網絡并非單純地使用批量標準化或譜標準化,而是將兩者有機地融合到判別器網絡中.具體地說,將SN 層加入到Sigmoid 層的前一層,其余層均使用BN 層.這樣設計的目的在于,充分地利用兩種標準化的優勢.BN 的主要作用是使前后兩層之間的分布盡量保持一致,減小每層網絡內部之間的協方差偏移(covariate shift),改善梯度更新過程,加速網絡收斂.而SN 的主要作用是使得每層網絡的Lipshitz 常數盡量逼近1,進而使得判別器網絡的訓練更加穩定,其作用等價于網絡正則化.由此看來,BN 與SN 之間并無沖突,其作用也不可相互替代.同時,無需顧慮SN 在網絡中的位置,根據BN 和SN 的原理,加入Sigmoid 層的前一層是最合理的位置.一般情況下,DCGAN 中Sigmoid 層的前一層網絡是壓縮層,將上一層的結果壓縮成N×1×1×1(N表示通道數),此時使用BN 并不能起到任何作用,但SN 不一樣,仍然能夠控制該層的Lipschitz 常數,并且此時的SN 仍能對模型產生正則化效果.從這個角度分析,SN 解決了BN 在Sigmoid 層的前一層網絡中失效的問題.因此,將兩者有機地融合到判別器中更有利于提升網絡的判別能力.圖3 所示為優化的DCGAN 網絡結構.

初始化策略及超參數設置是GANs 網絡結構的重要組成部分,這兩項配置對網絡結果有一定的影響.常用的GANs 網絡權重初始化是高斯分布(N(0,0.02)或均勻分布(U(0,1))隨機數.本文采用的初始化策略是判別器與生成器均使用正交初始化[25].這個初始化策略受到如下事實的啟發:隨機向量的正交變換的熵不變[19].需要特別強調的是,偏置項沒有初始化,因為卷積層的后一層加入BN 層或SN 層之后,該卷積層的偏置項并沒有發揮任何作用,所以一般將偏置項去除.除此之外,經過不斷的實驗,獲得了如下最優超參:懲罰因子λ=1,批量數為64,梯度優化算法使用OAdam(optimistic Adam)算法[30],其參數設為β1=0.5,β2=0.9,判別器的學習率lr_D為0.000 1,生成器的學習率lr_G為0.000 4,隱空間分布是128 維的標準高斯分布,網絡迭代率是2:1(即生成器每迭代1 次判別器需迭代2 次).接下來,通過實驗來證實網絡結構配置(包括超參數、初始化策略以及結構優化)的高效性以及懲罰模型的有效性.

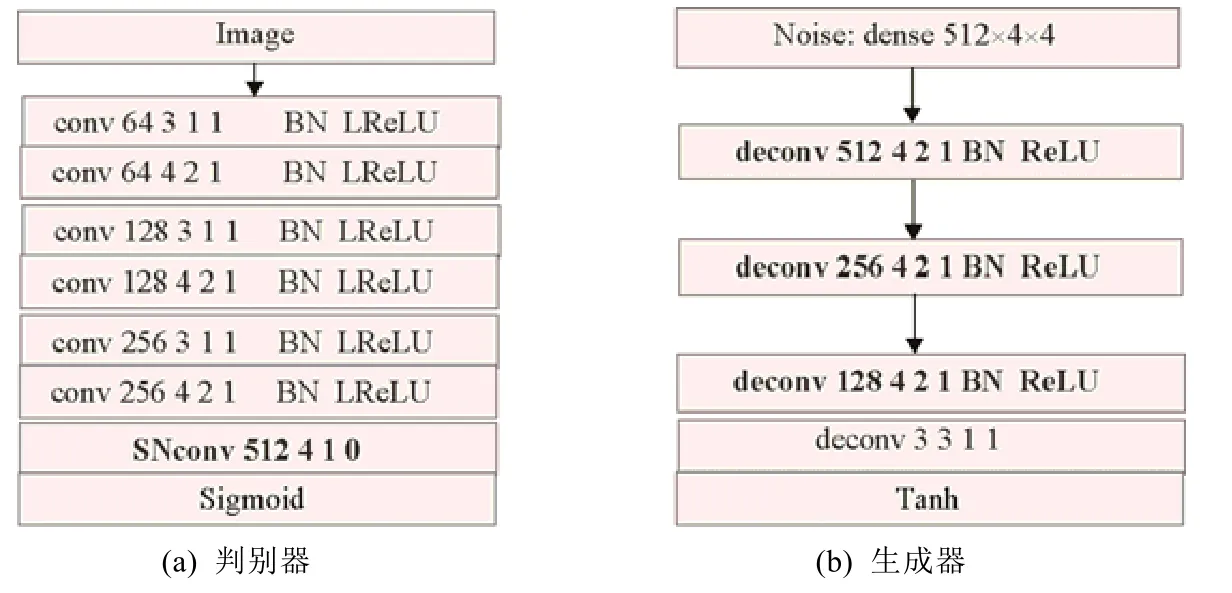
Fig.3 The optimized network structure of DCGAN (the image size is 3 × 32 × 32)圖3 優化的DCGAN 網絡結構(圖像尺寸為3 × 32 × 32)

3 實 驗

為了驗證EDGAN 算法的性能,本文在CIFAR10[31]、SVHN[32]、STL10[33]、CelebA[34]、LSUN[35]數據集上進行實驗,其中,LSUN 數據集只用bedroom 子集,共3 033 042 張圖片,同時與近年來的一些代表性算法作對比.所有實驗都在Pytorch 框架下完成,且數據集STL10、CelebA 和LSUN(bedroom)的圖像尺寸被統一剪裁為3 × 32 ×32.首先,在第3.1 節中簡述模型的評價標準;之后,在第3.2 節中驗證優化的網絡結構性能;然后,在第3.3節中對懲罰模型的有效性進行驗證;最后,第3.4 節是算法性能對比.

3.1 性能評價標準

目前在GANs 領域中,IS(inception score)得分[36]和FID(Frechet inception distance)值[37]是兩個最經典的性能評價指標,幾乎已成為該領域內通用的評價標準.IS 得分是利用在ImageNet 數據集上預訓練的InceptionV3網絡[38]對GANs 生成的樣本構建一個得分統計量,其表達式如下:

FID 值實質上是兩個假設的高斯分布之間的Wasserstein II 型距離[40].具體地,FID 值是利用inception V3 網絡(其他CNN 網絡也可行)分別將生成樣本與真實樣本嵌入到一個特征空間中,同時假設嵌入的樣本服從高斯分布,并分別計算嵌入樣本的均值μG、μd和協方差CG、Cd,則兩個分布之間的FID 值為

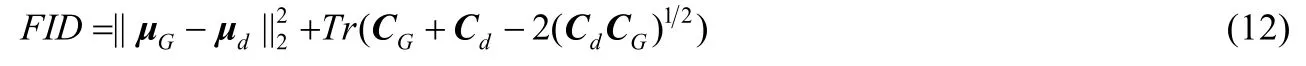
由FID 值的定義(12)可知,只要滿足高斯分布的假設,FID 值能夠很好地度量GANs 模型的性能.根據中心極限定理[41],若樣本容量趨于無窮大,則其極限分布服從高斯分布.于是,在實際中計算FID 時常常要求GANs 生成足夠多的樣本.由于FID 值是間接地度量生成分布與真實分布之間的距離,因此,FID 越小,模型的性能越好.相比IS 得分,FID 值更能全面地度量GANs 模型生成樣本的質量(無論是多樣性還是逼真度)[37],這個指標幾乎已成為GANs 領域內統一的評價標準.本文所有的實驗結果都僅以FID 值作為評價標準.在無特別說明的情況下,所有實驗的FID 值都是分別從真實樣本中抽取50 000 個樣本,從生成樣本中抽取50 000 個樣本而計算得出.

3.2 優化的網絡結構性能驗證

為了驗證兩種優化策略的有效性,即:(1) 將判別器倒數第2 層的卷積層修改為譜標準化的卷積層(如圖3(a)中倒數第2 層所示);(2) 刪除生成器中的311 不變層,在DCGAN 網絡結構上執行消融實驗(ablation study).為便于表示,用SN_in_P(SN in Penultimate)和R311(Remove 311)分別表示第(1)種和第(2)種優化策略.為簡化實驗過程,這個消融實驗僅在CIFAR 10 數據集上執行,生成器分別訓練70k、100k、140k 和200k 次.然后,將這種優化策略拓展到其他4 個數據集上來驗證其性能.CIFAR 10 數據集是由60 000 張32×32 的彩色圖片構成,其中有50 000 張圖片構成訓練集,10 000 張圖片構成驗證集,本文用到的數據集是去標簽后的訓練集(50 000 張).

表1 是兩種優化策略的消融實驗結果.表1 的結果顯示,SN_in_P 策略對DCGAN(表1 第2 行)的整體性能有所提升,但是提升幅度顯著差于R311 策略,尤其是訓練次數為140k 時,FID 值下降至26.27.可以看出,移除前(表1 中DCGAN)和移除后(表1 中R311)的結果形成了鮮明的對比.為了驗證兩種策略相結合的效果,我們分別實驗當批量數為128(表1 中第5 行)和64(表1 中第6 行)時,網絡的性能變化情況.可以看出,在4 種迭代次數下,兩種優化策略相結合的網絡性能均有不同程度的提升,FID 值均在下降.相比之下,當批量數為64 時,網絡效果更好.表1 所示結果充分證實,本文所提出的兩種優化策略是有效的,尤其是兩種優化策略相結合的網絡更是大幅度地提升了網絡的性能.

Table 1 Testing the effectiveness of optimization strategy on network structure (FID)表1 網絡結構優化策略的有效性驗證(FID)

為了全面地驗證兩種優化策略的效果,我們分別在CIFAR10、SVHN、CelebA 等5 個數據集上訓練兩種策略相結合的網絡.為便于表示,稱這個優化的網絡結構為OptimizedDCGAN.在這個實驗中,將批量數設為64.表1的結果已經顯示,批量數為64 比批量數為128 時的網絡性能更好.為了驗證這一事實,單獨對批量數執行消融實驗.圖4 是DCGAN 分別在CIFAR 10 數據集上訓練70k、100k、140k 和200k、批量數分別為64 和128 的結果.可以清晰地看出,批量數為64 的網絡(藍色)顯著優于批量數為128 的網絡(淺灰色).在無特別說明的情況下,后續所有實驗的批量數均設為64.表2 是OptimizedDCGAN 在5 個數據集上分別訓練70k、100k、140k 和200k次后的結果.

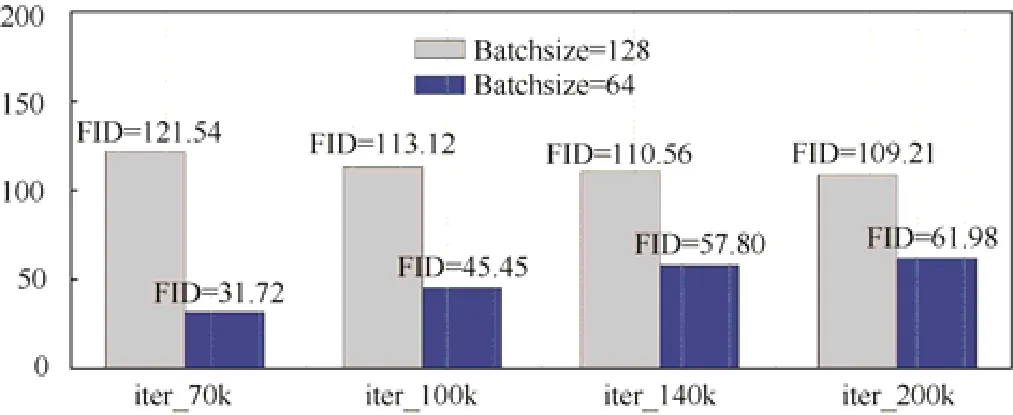
Fig.4 The effect of batchsize on network performance (CIFAR 10)圖4 批量數對網絡性能的影響(CIFAR 10)

Table 2 The performance of the optimized DCGAN network structure (FID value)表2 優化的DCGAN 網絡結構的性能(FID 值)

相比DCGAN 網絡結構,優化的網絡結構OptimizedDCGAN 的性能在5 個數據集上均有顯著的提升.值得強調的是,在SVHN 數據集上,DCGAN 在4 種訓練次數上的表現極不穩定,尤其是在訓練次數為140k 時,FID 值忽然從11.19(100k)上升至71.07,200k 時又下降至41.72,而OptimizedDCGAN 網絡結構表現較為穩定.表2 的結果再次驗證了本文所提出的網絡結構優化策略的有效性.

3.3 懲罰模型的有效性驗證

本節驗證由OptimizedDCGAN 網絡結構與條件熵懲罰相結合的懲罰模型的有效性.首先,探究懲罰模型一些關鍵參數的最優配置,包括迭代率、學習率以及初始化策略等;其次,驗證本文所提出的懲罰技術的有效性.

3.3.1 懲罰模型的參數配置及初始化策略

考慮到深度神經網絡對網絡參數配置的敏感性,我們通過一系列的消融實驗來確定一些關鍵的超參數及其初始化策略.通過反復實驗得到,懲罰模型的一些最優參數配置如下:懲罰因子λ=1,迭代率2:1(即生成器每更新一次判別器需更新兩次),判別器學習率lr_D=0.0001,生成器學習率lr_G=0.0004,梯度優化算法使用OAdam(0.5,0.9),初始化策略:判別器和生成器均使用正交初始化.下面,我們利用消融策略逐一驗證這些配置的有效性.為簡化驗證過程,所有消融實驗僅在CIFAR 10 上執行,生成器均訓練100k 次.

首先,確定最優的懲罰因子λ.在其他參數保持不變的前提下,觀察λ=0.1,1,5,10,15,20時網絡性能的變化情況,其結果顯示在表3 中.可以看出,當λ=1 時,網絡性能表現最佳,此時FID 值為14.02.其次,再觀察網絡學習率、迭代率、初始化策略、梯度優化算法對網絡性能的影響,每個目標觀察量均設置5 種變化,并統一表示為A、B、C、D、E.這些實驗結果均總結在表4 中,其中每個目標觀察量的5 種變化A～E的含義均置于FID 值的下方.由表4 的結果可知,當lr_D=0.0001、lr_G=0.0004 時,網絡性能表現最佳.從學習率的實驗結果還可以看出,這個參數對網絡性能的影響較大;特別地,當lr_D＞lr_G時(如表4 中B、D組合),網絡性能較差,反之,則較好(如A、C、E組合).為此,我們單獨執行實驗9 種學習率組合以探究這個有趣的現象,結果如圖5 所示.

Table 3 Different penalty factors and corresponding FID values on CIFAR 10表3 不同懲罰因子λ 所對應的FID 值(CIFRA 10)

Table 4 Implementing the ablation studies with respect to some hyper parameters and initialization (CIFAR 10)表4 一些超參數及初始化策略的消融實驗(CIFRA 10)

在圖5 中,藍色的點(LR1-LR4)表示lr_D＞lr_G的點,紅色的點表示lr_D≤lr_G的點.可以清晰地看出,藍色點的FID 值普遍高于紅色的點,這說明上述現象是存在的.對于迭代率,選擇2:1 較好.在初始化方法中,選用4 種初始化方法:正交初始化(Orth)[25]、Glorot 正態初始化(Glorot)[42]、高斯初始化N(0,0.02)以及Kaiming 正態初始化(KaiN)[43],5 種組合.

上面表4 的結果顯示,當判別器和生成器均實施正交初始化時,網絡性能最優.在梯度優化算法中,只選擇兩種優化算法(Adam,OAdam),不同參數下的5 種組合.已有研究表明,Adam 算法一般要優于其他優化算法[12,23,44],如SGD、RMSprop、Rprop 等算法.在懲罰模型中,選擇OAdam(0.5,0.9)較優.

Fig.5 The effect on network performance with different learning rates圖5 不同學習率對網絡性能的影響

3.3.2 懲罰技術的有效性驗證

為了充分體現本文所提出的懲罰技術的有效性,分別在CIFAR 10、SVHN、STL 10、CelebA 和LSUN 這5個數據集上執行如下實驗:(1) 不帶任何懲罰的網絡(no-penalty);(2) 利用條件熵距離懲罰生成器的網絡(EDGAN);(3) 利用Jensen-Shannon(JS)散度(對稱版本的KL 散度)懲罰生成器的網絡(with-JS-penalty);(4) 利用WGAN-GP[12]中的梯度懲罰技術懲罰判別器、條件熵距離懲罰生成器,即雙懲罰網絡(with-bi-penalty),其中,判別器懲罰因子沿用WGAN-GP 中的設置(懲罰因子為10,Lipschitz 常數為1).同樣,所有生成器均訓練100k 次,實驗結果見表5.特別需要強調的是,表5 第2 列的結果(不帶懲罰的網絡)與表2 訓練100k 次時的結果不一樣,主要是由于兩個網絡使用的參數及初始化策略不一致,前者使用第3.3.1 節中的參數及初始化配置,而后者使用DCGAN 中的配置.首先,觀察不帶懲罰的網絡(表5 第2 列)與帶條件熵距離懲罰生成器的網絡(表5 第3 列,本文提出的算法),5 個數據集所對應的FID 值均有不同程度的下降,網絡性能獲得提升.這充分說明,本文所提懲罰技術是有效的.其次,再觀察帶JS 懲罰的網絡(表5 第4 列)以及雙懲罰網絡(表5 最后一列),5 個數據集上的FID值均大于第3 列的FID 值(EDGAN),這也充分證實,本文所提出的懲罰技術具有明顯的優勢.

Table 5 Verifying the penalty effect of EDGAN algorithm:The generator iterates 100k times (FID value)表5 驗證EDGAN 算法的懲罰效果:生成器更新100k 次的FID 值

3.4 整體性能對比

上述一系列實驗可驗證得出,EDGAN 算法能夠顯著提高GANs 網絡的性能.為了更進一步地驗證EDGAN的優越性,現將該算法與近年來的一些代表性算法作比較.本文在5 個數據集上訓練LSGAN(2017)、WGAN GP(2017)和SNGAN(2018)等5 種算法,其結果顯示在表6 中.其中,表6 最后一列表示最優結果的生成器迭代次數,最后一行是真實數據的FID 值.從表6 所示結果可以看出,EDGAN 算法在多個數據集上都超越了目前的一些經典算法,只有在SVHN 和LSUN 數據集上稍遜于GAN-0GP和LSGAN 算法.與此同時,EDGAN 在CIFAR 10、STL 10 和CelebA 數據集上的FID 值更進一步地接近真實數據集的FID 值.表6 中加灰色的行是SAGAN 算法,這是一種經典的條件GANs 算法,而這里是將其標簽信息從算法中刪除,此時,SAGAN 算法就退化為無條件的GANs(即GANs).在此執行這個實驗,意在說明是否可將條件GANs 的優良性能移植到無條件GANs 上?SAGAN在5 個數據集上的實驗結果表明,答案是否定的.這也充分證實這樣的一個事實:條件GANs 并不能當作無條件GANs 來使用.因此,開發高性能的無監督圖像生成算法成為本文研究的出發點.

Table 6 Comparison of the algorithm performance表6 算法性能對比

4 結束語

本文利用條件熵距離對GANs 生成器的目標函數進行懲罰,其目的是在保持樣本多樣性的條件下迫使生成分布盡可能地接近真實分布,這使得GANs 生成的樣本既有多樣性又具有高逼真度,從而能夠提高GANs 生成樣本的整體質量.除此之外,本文在DCGAN 網絡結構的基礎上,對GANs 的網絡結構進行優化,其中包括:(1) 根據批量標準化和譜標準化的互補特性,將兩個標準化技術有機地融入到判別器網絡中,以提高網絡的判別能力;(2) 去除生成器網絡中的311 尺度不變層,提升生成器的生成能力,同時也可縮小生成器網絡的參數空間,以此提高網絡的訓練效率及性能;(3) 改變兩個網絡的初始化策略,判別器網絡和生成器網絡均使用正交初始化.最后,將懲罰的GANs 目標函數與優化的網絡結構相結合,形成條件熵距離懲罰的GANs,即EDGAN.實驗結果表明,EDGAN 算法已經超越了目前的一些經典GANs 算法.

雖然本文通過實驗驗證EDGAN 可以提高GANs 生成樣本的質量,但其收斂性理論問題仍有待進一步加以研究.另外,如何利用EDGAN 生成的樣本解決一些無監督問題,即EDGAN 的下游問題,仍有待深入研究.