基于隱馬爾可夫的滾動軸承健康狀態評價方法研究*

鄭小霞,劉 靜,魏彥彬,蔣海生

(上海電力大學 自動化工程學院,上海 200082)

0 引 言

滾動軸承在旋轉機械上應用比較廣泛,它的工作狀態影響著運行機械的工作精度[1]。滾動軸承是發電機傳動系統中最易受損的主要部件之一,若發生故障會對整個機組的運行狀態產生很大影響,造成很大的經濟損失[2]。因此,為保證發電機組的可靠性和安全性,降低維修成本,并提高其運行效率,對滾動軸承進行健康狀態監測具有重要的意義[3]。

滾動軸承的振動監測信號是非平穩的復雜信號,其頻率成分復雜,且根據實際狀況的影響,該信號會不斷發生變化,諧波、干擾與故障特征頻率之間也容易出現重疊現象。因此,采用傳統的方法難以提取其故障信息[4]。

小波包分解是一種典型的復雜非平穩信號處理方法,能對信號進行精確的處理,被廣泛用于各類設備的狀態監測中[5，6]。文獻[7]通過小波包分解提取信號特征,進行了發電機組齒輪箱的故障診斷。文獻[8]為了解決運行中監測信號噪聲的影響,基于小波包分解,提出了一種評價不同頻帶故障的方法。

互補聚合經驗模態分解(CEEMD)是由YEH J R[9]提出的一種常用的信號特征提取方法,能對信號進行很好的分解,并減少重構誤差的產生。文獻[10]通過CEEMD方法,將風速劃分為一組固有模態函數,并結合極限學習機(ELM)實現了對風速的預測,但是該方法不能完全消除模態混疊。

對于提取的故障特征信號,需要選擇合適的模型來進行設備的健康狀態評價。隱馬爾可夫模型(HMM)是由LeonardE.Baum提出的一種描述隨機過程的概率模型,該模型對于復雜的時間序列有很好的建模能力,被廣泛應用于設備的壽命預測和狀態評價[11]。文獻[12]通過隱馬爾可夫模型進行了齒輪箱的功能退化檢測,推導出了其性能的下降規律。但在實際應用中,隱馬爾可夫模型容易出現過度擬合問題;而變分貝葉斯(VB)優化的隱馬爾可夫(HMM)模型對發電機組軸承部件則有著更好的適用性。

綜上所述,筆者提出一種基于小波包-互補聚合經驗模態分解和變分貝葉斯-隱馬爾可夫模型的滾動軸承健康狀態評價方法,并利用軸承退化的實驗數據對該模型進行驗證。

1 基于小波包的CEEMD特征提取

互補聚合經驗模態分解(CEEMD)適合非線性信號分析,可自適應地將復雜信號分解成由高頻到低頻的特征模態函數(IMF)[13]。CEEMD算法原理與EEMD算法一致,只是分解過程中加入了成對的白噪聲,能夠減少由白噪聲引起的誤差,更準確地對原始信號進行重構[14]。

由于原始信號中的頻率成分比較復雜,CEEMD很難得到單分量IMF。針對這一問題,可選擇小波包分解(WPD)對原始振動信號進行預處理,以降低振動信號的復雜性,抑制CEEMD分解過程中出現模態混疊問題。WPD不僅能對低頻部分進行分解,對高頻信號也有具很好的分解能力,保證其良好的分辨率。

應用小波包分解時,首先要根據分解的數據類型進行小波基函數的選取。筆者主要依據降噪后信號的完整度和準確度選擇小波基函數。另外,小波包的分解層數的選取也很重要,分解層數過小,不能體現信號的細節信息;分解層數過大,計算量會增加。所以根據研究和計算,筆者采用db3小波基對原始信號進行3層分解,并計算第3層各節點信號的能量占比,取總能量高于80%,且能量較大的信號進行重構,由此可以消除大部分的干擾信號,為下一步的CEEMD分解奠定基礎。

采用改進的CEEMD方法,首先要對原始信號進行小波包降噪,以降低信號的頻率分量,再利用CEEMD將降噪后的信號分解為IMF分量,根據相關系數選擇有效分量進行重構,最后提取出故障的特征信號。

2 隱馬爾可夫模型及其改進

2.1 隱馬爾可夫(HMM)原理

HMM模型是一種用來描述含有隱藏未知參數的馬爾可夫過程的統計模型,其狀態序列為隱藏的馬爾可夫鏈隨機生成的不可觀測序列;每個狀態生成一個觀測,再由此產生的觀測的隨機序列,稱為觀測序列[15]。

假設觀測序列Y={y1,y2,…yr},可以表示為二變量過程(S,Y)={(st,yt),t=1,2,…,T}。隱含過程{st}是一個馬爾可夫鏈。

隱馬爾可夫模型可用θ=(π,A,B)來描述,分別定義為:

(1)狀態轉移概率矩陣:A={aij,i,j∈S},aij=P(st=j|st-1=i);

(2)發射概率矩陣:B={bim,i,m∈S},bjm=P(yt=m|st=i);

(3)初始狀態分布:π={πi,i∈S},πi=P(s1=i)

假設A、B和π之間相互獨立,先驗概率為:

P(θ)=P(π)P(A)P(B)

(1)

由于狄利克雷分布與似然項共軛,所以選擇參數π、A、B的先驗概率為Dirichlet分布:

(2)

(3)

(4)

式中:uA,uB,uπ—狄利克雷分布參數;M—觀測數目;I—狀態數。

2.2 變分貝葉斯(VB)原理

在貝葉斯算法中,對參數邊緣化過程中需要進行積分運算,這個計算會影響信號處理的可行性,所以此處采用變分貝葉斯來解決這個問題。

logp(Y)=logp(Y,Z)-logp(Z|Y)

(5)

logp(Y)=log{p(Y,Z)/q(Z)}-
log{(p(Z│Y)/q(Z)}

(6)

兩邊積分為：

(8)

后驗分布p(Z|Y)的估計和模型證據p(Y)可表示為:

logp(Y)=L(q)+KL(q‖p)

(9)

其中,定義:

(10)

(11)

式中:L(q)—下界;KL(q‖p)—q和真實后驗p之間的KL。

使KL最小,相當于使L(q)最大,最大化過程即是通過迭代潛在變量和參量的后驗概率。

2.3 隱馬爾可夫模型的改進

隱馬爾可夫模型求解參數時采用的是極大似然估計(maximum likelihood estimate,MLE),沒有考慮模型的復雜性。而對于一個隱馬爾可夫模型而言,其復雜性與模型中的狀態轉移矩陣A的連通度、隱藏狀態數量t和發射矩陣B中,每個隱藏狀態對應觀察狀態的概率分布有關。所以,在實際應用中,如果有很多觀察數據,擬合參數的數量可能會超過可用的數據量,造成結果的不準確。

為解決這個問題,筆者提出了一種變分貝葉斯算法改進的隱馬爾可夫模型,采用變分貝葉斯(VB)代替極大似然估計(MLE),來求解HMM中的模型參數,對發電機組復雜信號的建模具有更好的效果。

變分貝葉斯(VB)是一種在貝葉斯估計和機器學習領域中用于近似復雜積分的技術[16]。在貝葉斯算法中,在參數邊緣化時往往需要積分運算,而在進行實際信號處理時,該運算會影響信號處理的可行性。采用變分貝葉斯則可解決了一問題。

變分貝葉斯(VB)本質上是一種近似算法,即對難以求解的后驗分布進行近似求解。在變分推斷中,經常用一個簡單分布q(Z:φ)來近似復雜分布p(Z|Y,θold),從而得到一個局部最優,且有確定解的近似后驗分布。

變分貝葉斯改進隱馬爾可夫的具體步驟為:

在上文的HMM中,隱含狀態和觀測數據的似然函數為:

(12)

(13)

由貝葉斯公式得出參數的后驗密度為:

(14)

其中,分母中的積分是無法處理的,因此,此處引進變分貝葉斯作為一種處理方法。

邊緣似然表示為:

(15)

兩邊對其取對數,再取關于后驗分布q(S,θ)的期望,有:

(16)

式中:q(S,θ)—潛在變量和參數的變分后驗。

把它們的組合表示為Z(S,θ)。logP(Y)的估計可以通過使KL散度最小來實現,也等價為使下界最大。

下界可表示為:

(17)

(18)

對上式關于參量θ狀態S的后驗求偏導,可得到VBM-step和VBE-step中的迭代方程:

(1)VBM-step:

(19)

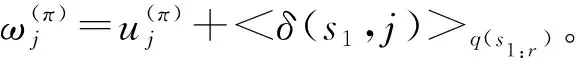
(20)

(21)

(2)VBE-step:

(22)

(23)

(24)

此處仍應用前向-后向算法,有:

(25)

(26)

設前向概率值為DI,其可表示為:

(27)

2.4 發電機組健康模型的建立

發電機組運行環境特殊,且難以取得完備的運行數據,故筆者將采集的健康狀態信號作為模型訓練樣本,建立變分貝葉斯-隱馬爾可夫(VB-HMM)健康狀態模型;再將監測到的當前數據輸入到模型中,得到當前狀態與健康狀態的接近度,實現對軸承的健康狀態評價。

在所建立的VB-HMM模型中,每一組數據對應一個對數似然概率值,來表示健康狀態評價結果。

建立發電機組滾動軸承健康狀態評價模型的具體步驟如下:

(1)采用小波包分解對軸承振動信號進行預處理,提取能量較大且總能量高于80%的節點信號;

(2)將步驟(1)提取的節點信號進行CEEMD分解,取相關系數大于0.9的IMF分量作為特征信號;

(3)用健康數據訓練健康狀態模型;

(4)將樣本數據輸入到健康狀態模型中,得到對數似然概率值,對訓練結果進行分析。

3 實驗信號分析

3.1 實驗臺參數

此處筆者利用美國辛辛那提大學智能維護系統中心(IMS Center)提供的軸承全壽命疲勞試驗數據進行軸承的退化過程驗證。

該實驗裝置包括4個雙列滾子軸承,筆者在每個軸承外座處安裝一個采樣頻率為20 kHz的PCB353B33加速度傳感器,并對軸承施加266 689 N的徑向力。

實驗中軸承傳感器的布置示意圖如圖1所示。

圖1 傳感器布置示意圖

3.2 小波包分解

筆者將軸承的部分故障原始信號進行小波包分解;采用db3小波基,將信號分解為3層,此時可保證故障信號完整,且可最大限度地消除干擾信號。

進行小波包分解后,第3層的8個頻帶節點的能量分布如圖2所示。

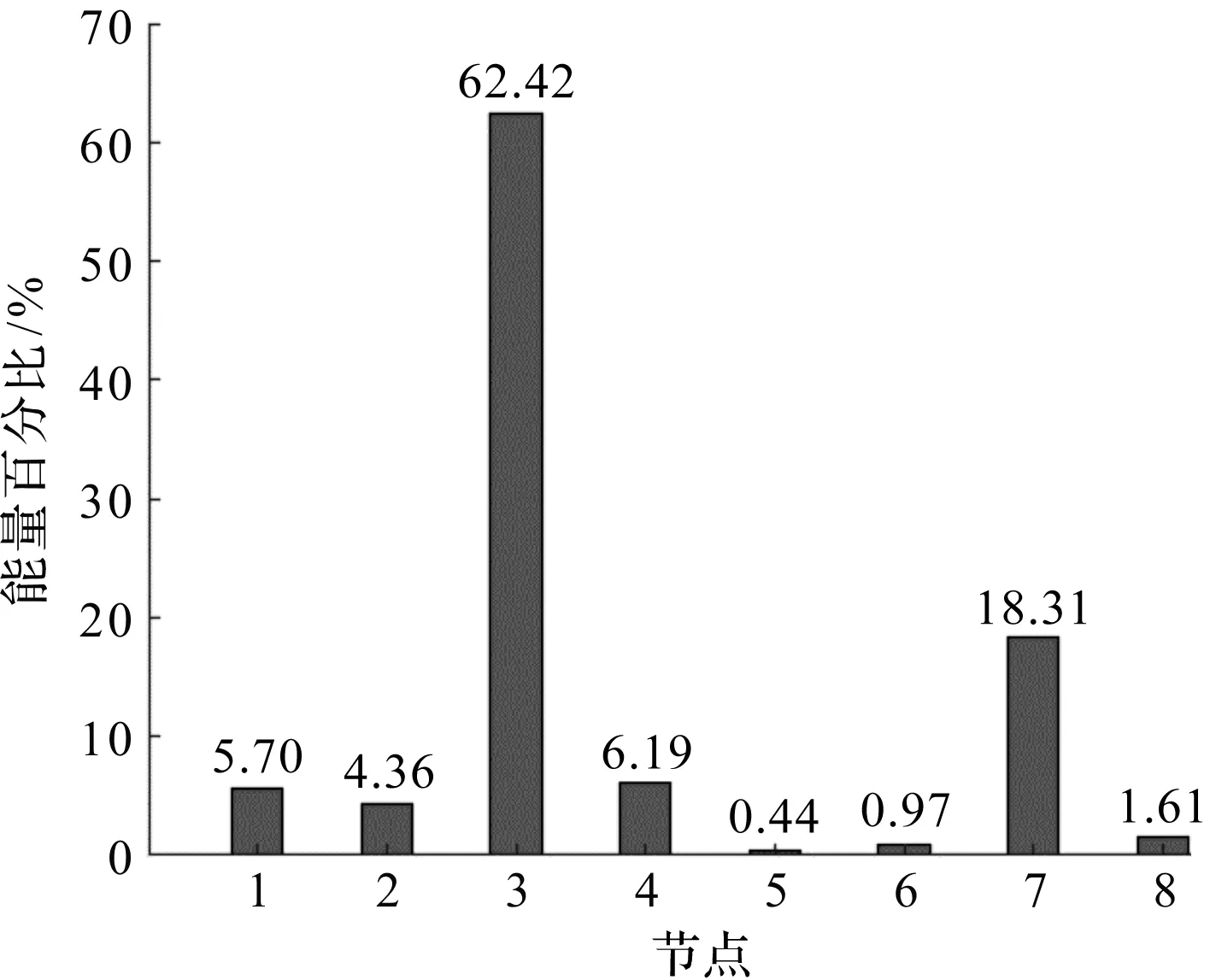
圖2 軸承故障振動信號頻帶能量分布

由圖2可看出:軸承故障振動信號的能量主要集中在節點3和節點7,占到總能量的80%以上,因此,此處對節點3和節點7進行重構。

原始信號和重構后的信號頻域波形如圖3所示。

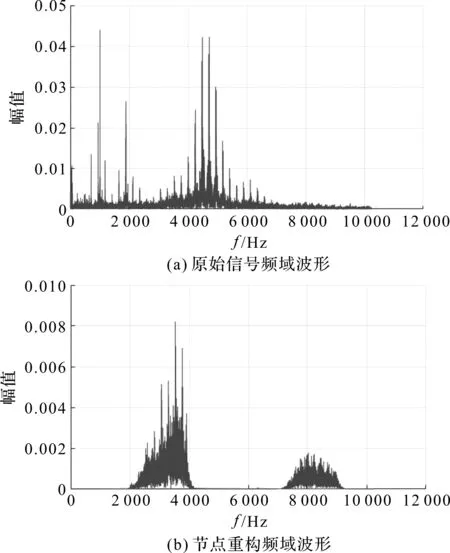
圖3 原始信號和小波包分解后的頻域波形

3.3 CEEMD信號分解

對軸承的原始振動信號進行小波包降噪預處理后,筆者根據能量分布提取能量較高的節點3和節點7,再進行CEEMD分解,以消除其他干擾信號和虛假分量,提取出故障的特征信號。

節點3和節點7分解后,IMF分量的時域波形如圖4所示。

圖4 IMF分量時域波形

兩節點重構后的IMF分量與小波分解后的原信號的相關系數如表1所示。

表1 IMF分量與小波分解后的原信號的相關系數

提取相關系數高于0.9的分量作為故障特征信號,其余IMF信號與原信號相似性較低,作為干擾信號舍去。

3.4 變分貝葉斯-隱馬爾可夫健康模型的建立

筆者選擇辛辛那提大學軸承疲勞數據中的SET-2中的849組數據作為實驗數據,建立軸承的全壽命周期曲線。每組數據有20 480個數據。為方便后面的計算,把每組數據分為20段,每段1 024個數據;選擇其中的200組健康狀態數據訓練健康狀態的模型參數,剩余的649組作為測試數據;將所有數據進行小波包分解,并根據上文中的分析提取3、7節點的數據進行CEEMD分解,提取相關系數高于0.9的IMF分量作為特征向量,進行健康模型訓練。

為比較隱馬爾可夫模型(HMM)和變分貝葉斯-隱馬爾可夫模型(VB-HMM)的區別,此處采用相同的數據分別對兩種模型進行訓練和測試,得到的結果如圖5所示。

圖5 似然對數曲線

圖5中,為方便進行比較,兩個曲線圖取相同的縱坐標。從縱坐標來看,圖5(a)曲線的極值相差70個單位的DI值,圖5(b)中極值相差150個單位的DI值,所以圖5(b)中的曲線變化趨勢更加明顯。

由圖5可明顯看出:200組后,圖5(b)曲線開始明顯下降,但圖5(a)曲線沒有表現出下降趨勢;330組后,圖5(b)曲線開始有大幅度振蕩,圖5(a)中只有較小幅度振蕩。由此可見,變分貝葉斯-隱馬爾可夫(VB-HMM)模型更適合軸承健康模型的建立。

再用圖5(b)對實驗臺軸承的健康狀態進行分析。圖5(b)中,進行軸承健康狀態檢測的有649組數據。在實驗開始的1組～200組中,曲線很平穩,且對數似然概率值(DI)較大,說明這200組數據是健康數據,軸承處于健康狀態;隨著時間推移,201組～330組的曲線開始緩慢下降,表明軸承性能逐漸偏離健康狀態,開始劣化;在實驗后期,331組～649組數據的曲線開始有較大波動且下降嚴重,并在最后下降到最低點,表明軸承性能處于嚴重受損狀態。

由此可以看出:整個曲線可以描述軸承從健康狀態到逐步劣化,再到失效的整個過程。所以,本文的健康狀態評價模型能夠準確地評價軸承的健康狀態。

4 實驗臺實測數據分析

為了進一步說明采用變分貝葉斯-隱馬爾可夫模型對軸承數據進行準確評價的有效性,筆者采用滾動軸承加速實驗平臺的數據進行驗證。采用測量裝置采集滾動軸承整個壽命周期的振動信號。其中,加速度計型號為DYTRAN3035B,振動信號的采樣頻率為25.6 kHz;每次采樣間隔為10 s,采樣個數為2 560個;滾動軸承的轉速為1 800 r/min,載荷為4 000 N。

筆者將軸承振動信號的部分故障數據進行特征提取。首先對原始振動數據進行小波包分解預處理,分解后的能量分布如圖6所示。

圖6 軸承故障振動信號頻帶能量分布

圖6中,該軸承信號的能量集中在節點6,所以筆者提取節點6進行信號重構,并進行CEEMD分解。

各IMF分量與小波分解后的信號的相關系數如表2所示。

表2 IMF分量與小波分解后的原信號的相關系數

筆者取相關系數高于0.9的IMF分量,作為特征信號進行模型訓練;選取1 860組平臺數據建立變分貝葉斯-隱馬爾可夫模型。其中,取600組健康數據進行模型訓練,取1 260組數據進行測試。

筆者將每組數據分成10段,每段256個點,得到的軸承的對數似然曲線如圖7所示。

圖7 似然對數曲線

從圖7的實驗臺軸承全壽命周期曲線可知:

(1)前400組數據的DI值較大,表明軸承處于健康狀態;(2)第400組開始,數據的DI值開始降低,表明此時軸承開始劣化并保持劣化狀態繼續運行;(3)第900組數據,DI值進一步降低,表明軸承狀態持續劣化;(4)從1 200組數據到運行結束,軸承的DI值持續降低并出現最低點,表明軸承加速劣化直至失效。

由此可見,本文中的實驗方法對實測平臺數據仍然適用。

5 結束語

結合小波包-CEEMD特征提取和VB-HMM的優點,筆者提出了一種基于小波包-互補聚合經驗模態分解和變分貝葉斯-隱馬爾可夫模型的滾動軸承健康狀態評價方法,建立了發電機組滾動軸承部件的健康狀態評價模型;采用標準軸承數據和實驗臺實測數據進行了驗證,很好地反映了軸承部件的性能退化過程,為制定運行維護策略提供了參考。

研究結果表明:該模型輸出的對數似然概率值可作為指標進行狀態評價;對數似然概率曲線的變化均能反映軸承的健康、劣化和失效的運行狀態,該實驗方法具有很好的適用性。