計及風光出力相關性的風光互補發電系統優化

趙星虎，張會林

（上海理工大學機械工程學院，上海 200093）

0 引言

目前，隨著新能源的開發，以風力發電與光伏發電為代表的可再生新能源正成為中國乃至世界的重大電力能源。不同于傳統化石燃料燃燒會帶來環境污染等后果，新能源的開發有益于能源結構改革。但是由于風能和太陽能作為清潔能源，容易出現風光不確定問題，對系統并網造成了很大困難。國內外學者研究側重點通常集中在單一的能源并網運行控制策略和優化調度上，如文獻［1］通過分析發現風能和太陽能具有較好的資源互補性，可以進行共同發電；文獻［2］采用CSEA 算法提高了初代種群的多樣性，并選擇蒙特卡洛隨機法生成天氣情況，采用威布爾分布法生成風速情況，但其得到的模型難以接近實際情況；文獻［3］采用能量調度策略，通過遺傳算法得到最優的風光儲組合；文獻［4］、［5］以成本和失負荷概率為優化目標，采用粒子群算法以及多種啟發式方法相結合，實現風光互補發電系統的優化配置，解決了粒子群算法的局部收斂和早熟問題，但都未考慮安裝點當地的實際環境情況；文獻［6］考慮風光聯合分布，綜合考慮蓄電池壽命，根據市場實際情況進行調控。

本文綜合考慮風光出力相關性，探討該地區環境是否適合風光聯合發電［7］。采用Frank Copula 理論［8］，綜合考慮該地區風力發電和光伏發電的出力相關性，探討該地區在不同季節的風光出力相關性，以及能否進行風光聯合互補發電；利用Kendall 秩相關系數法進行不同季節的出力相關性對比，并建立風光聯合密度分布函數，得到風光聯合出力場景；采用NSGA-II 算法進行風光互補發電系統多目標容量優化，通過對不考慮風光出力相關性的系統與考慮風光出力相關性的系統進行3 種指標參數對比，得到風光互補系統優化配置。

1 風光相關性

1.1 太陽能輻射量計算

根據某一地區的天氣統計情況，得到一年的月平均太陽能輻射量以及月平均風速。

針對太陽能的光照強度計算，設計了一個太陽能小時數法SHM（Solar Hour Method），如圖1 所示。

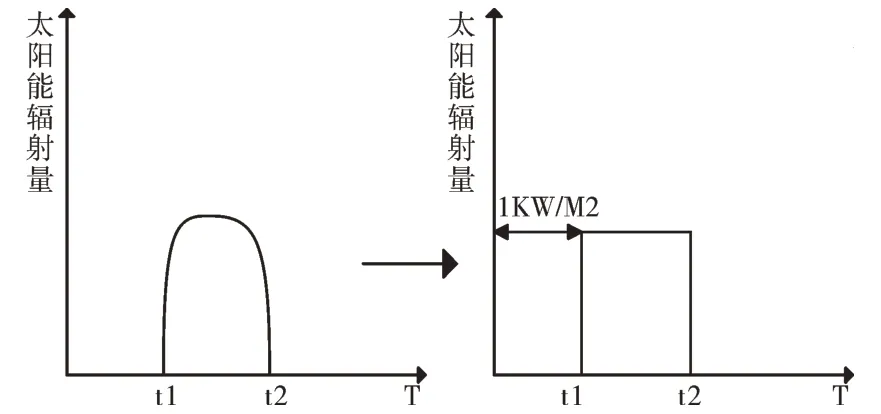
Fig.1 Solar hour method圖1 太陽能小時數法SHM

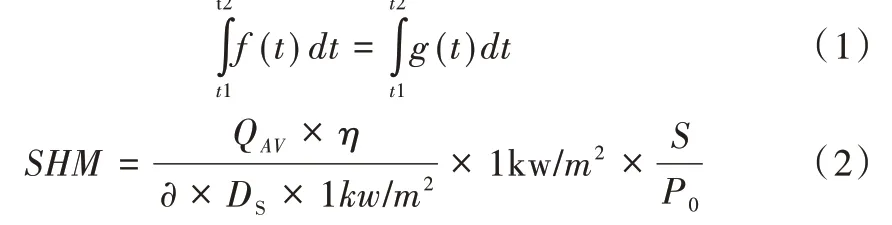
式中，DS為晴天天數；QAV為月平均輻射能量；η為太陽能電池板發電效率，設為0.14；?為能量轉化系數，設為3.6；S為太陽能電池板面積。

SHM 是將每日太陽能電池板所吸收的太陽能輻射量等效轉化為1KW/m2的發電小時數。對于太陽能輻射量統計，一般統計月平均太陽能輻射量，通過公式計算該月平均晴天太陽能電池發電小時數。

1.2 風光聯合概率分布

考慮到風光出力具有良好的互補特性，而Frank Copu?la 函數可以很好地描述變量之間的負相關特性［9-10］。本文選擇Copula 函數求解風光互補發電的聯合概率分布函數和密度函數為：

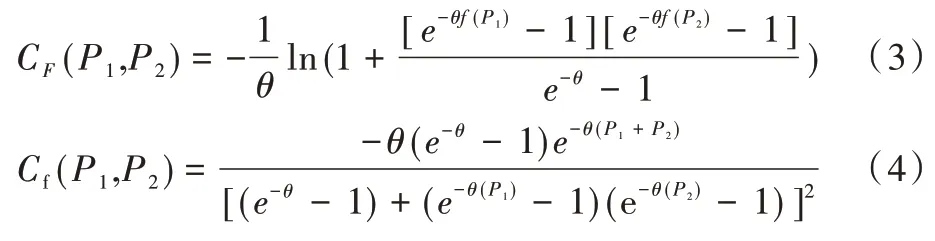
式中，θ為相關參數，P1、P2分別為風力放電和光伏發電出力率。當θ>0，表示P1與P2正相關；當θ=0，表示二者相互獨立；當θ<0，表示二者負相關。

根據月光照強度以及已知的月平均風速，繪制各月光照與風速對比圖，如圖2 所示。

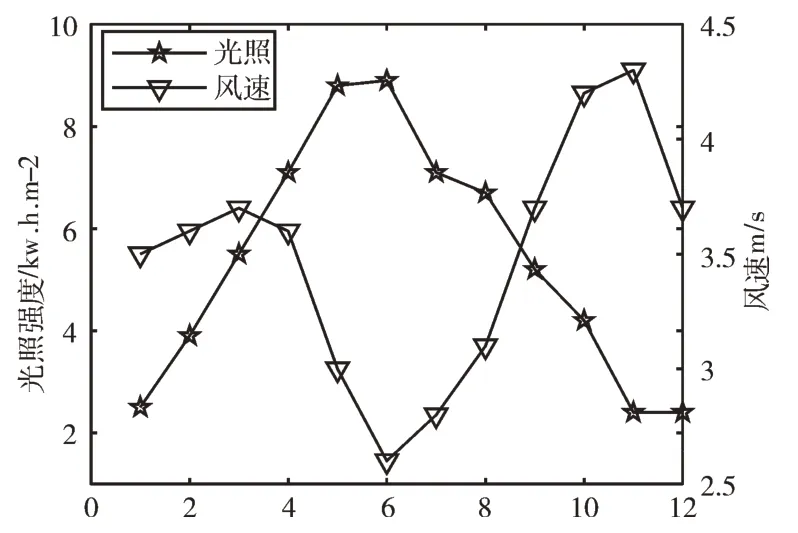
Fig.2 Comparison between monthly light and wind speed圖2 各月光照與風速對比

根據圖2 中的各月份平均光照強度和平均風速對照，該地區3-10 月光照強度高于風速，5、6 月達到最高值；風速表現為夏季5-7 月較低，冬季10-12 月較高，風速在冬季大于光照強度的數值。通過圖2 數據可初步判斷該地區的風速與光照在不同季節呈現互補特性，正好解決了單一能源受地理環境限制的問題。

Kendall 秩相關系數法基于隨機性的變量排序，反映了變量之間的單調性，即變化趨勢的一致性［11］。秩相關系數τ定義為：

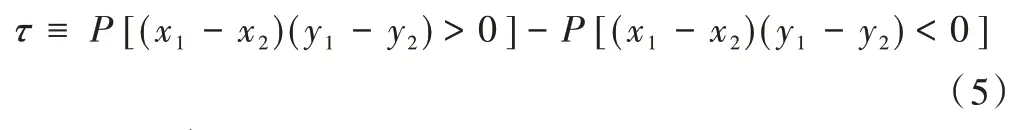
式中，{(x1,y1),(x2,y2)…,(xn,yn)} ∈φ(P1,P2)為風力發電和光伏發電的組成樣本觀測值。其中，參數θ與秩相關系數τ關系如下：

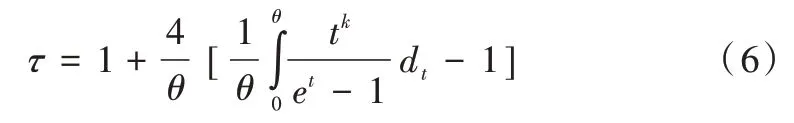
根據以上公式，可得到該地區的Kendall 秩相關系數τ=-0.513，相關系數θ=-6.98，以及不同季節的風光出力相關性。如表1 所示，風光出力呈現負相關性。

Table 1 The correlation of the output of different seasons表1 不同季節風光出力相關性

由表1 可知，夏季與冬季風光出力具有很強的負相關性，符合變化趨勢的一致性，具有可靠的互補特性。從表中數據看出，該地區通過風光互補聯合發電，能很好地彌補太陽能與風能的發電量差異，從而達到互補供電的目的。

2 風光互補發電系統多目標數學模型

在計及風光出力相關性的基礎上，考慮系統初期建設的經濟成本、系統供電可靠性，以及清潔能源利用率等因素，旨在得到計及風光出力的最優風光互補發電系統容量配置。

2.1 目標函數

（1）投資成本F。

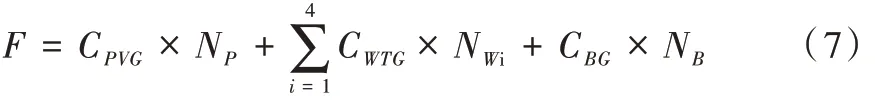
式中，CPVG為太陽能電池成本，CWTG為第i種風機成本，CBG為蓄電池成本，NP、NWi、NB為各器件數目。

（2）負荷缺電率LPSP。系統產生的能量不能滿足負荷需求的概率為負荷缺電率，如式（8）所示。

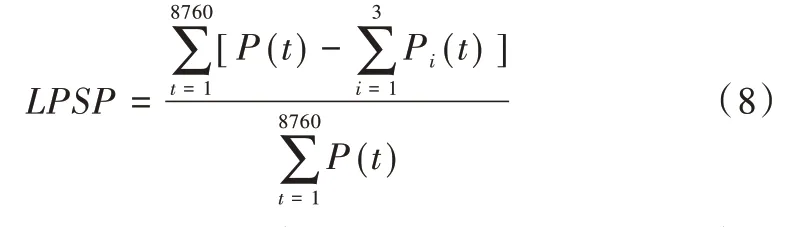
式中，P(t)為負荷所需功率，Pi(t)為各器件輸出功率。

當LPSP=0 時，表示系統每天都能滿足負荷功率需求；當LPSP=1，表示所有時間都不能滿足。故為了提高系統供電可靠性、滿足負荷需求，LPSP 需要盡可能地小。一般當LPSP<0.1 時，即可滿足負載端用電的可靠性。

（3）棄風棄光浪費率LOEP。即系統在運行過程中供給的能量溢出占全部負荷需求電量的比，表達式為：

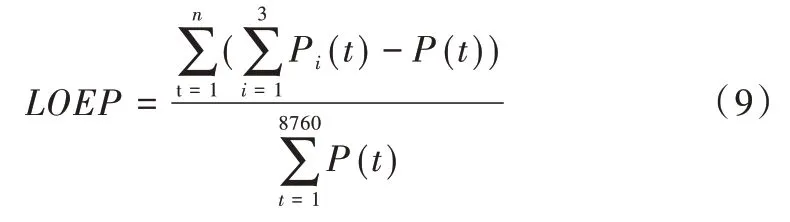
式中，n 為系統在某個時間內產生功率溢出導致甩負荷浪費的次數。故得出LOEP 越小，系統越可靠。

2.2 約束條件

（1）系統中風力發電機數目：

式中，nWTGmax為風力發電機最大數目，Qload為負載所需功率，Qwu為風機的單位發電功率。

（2）系統中光伏陣列最大數量［12］：

式中，nPWGmax為系統光伏電池最大數量。

（3）風機運行條件約束：

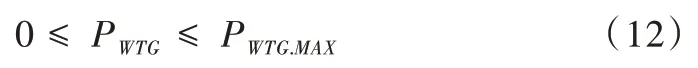
式中，PWTG.MAX為風機最大出力。

（4）光伏發電運行條件約束：

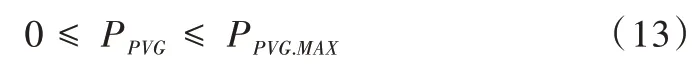
式中，PPVG.MAX為光伏最大出力。

（5）蓄電池功率約束：

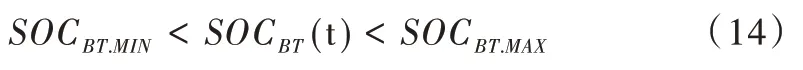
式中，SOCBT(t) 代表儲能電池所帶電荷量；SOCBT.MAX、SOCBT.MIN分別為蓄電池荷電狀態上下限［13］。

3 NSGA-II 算法

NSGA-II 算法是非劣等分類遺傳算法，引進了快速非支配排序算法和精英策略。通過擁擠度和比較算子簡化算法計算復雜性，使帕累托Pareto 最優解可能擴展到整個帕累托域，以確保整個種群的多樣性，從而得到分布均勻、多樣性強的非主導解集。計算原理如下：

（1）隨機生成規模為N 的父代種群P0，記為t=0；對種群Pt進行非支配性排序，得出適應度值。

（2）進行選擇、交叉、變異，生成一個新的子代種群Qt。

（3）將進化的父代Pt和子代Qt組合為2N 規模的種群Rt，對其重新進行非劣排序。

（4）在Rt最優前端，由低到高進行擁擠度排序，選擇N個個體至下一代Pt+1。轉到步驟（2），得到新的子代種群Qt+1，將子代與父代重新組成新種群Rt+1。

（5）如果t 小于設定的迭代數值，重復上述步驟，直到滿足條件為止。

計及風光出力相關性優化流程如圖3 所示。

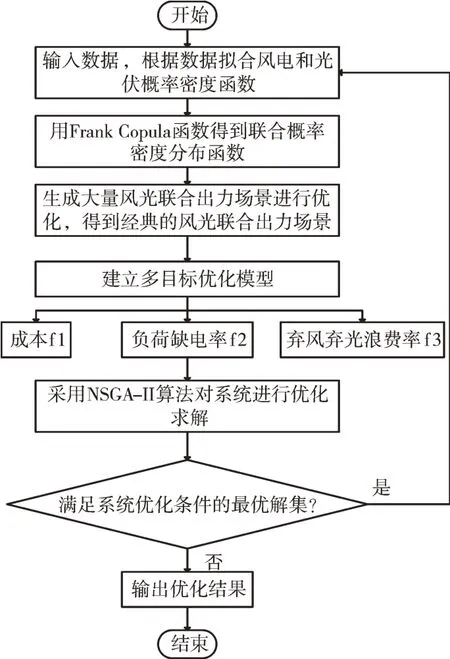
Fig.3 Optimization process considering landscape output correlation圖3 計及風光出力相關性優化流程

4 算例分析

在計及風光相關性條件下進行風光互補發電系統優化設計仿真。已知該地區一年的天氣情況和風速值，通過Frank Copula 函數進行風光聯合概率分布，探討該地區風光出力相關性。本文采用NSGA-II 算法對風光互補系統進行優化配置，種群規模N=200，編碼方式為整數編碼，演化代數設定為100 代，交叉概率為0.7，變異為0.05，并通過設定的自適應策略進行調整。經過算法優化，得出計及風光出力相關性系統容量最優配置。

圖4 為優化后的整個系統發電曲線和負荷曲線。從全年曲線可以看出，夏季光伏發電量多，風力發電量少，而冬季光伏發電量少，風力發電量增加，正好與圖2 的風速及光照圖相對應，具有非常好的負相關性，夏季和冬季尤其明顯，彌補了太陽能和風能的季節性差異，既能穩定地為負荷供電，提高系統供電的可靠性，又能提高風光互補發電效率，形成良好的風光互補特性。

不考慮風光出力相關性與考慮風光出力相關性兩種情況對比如表2 所示。

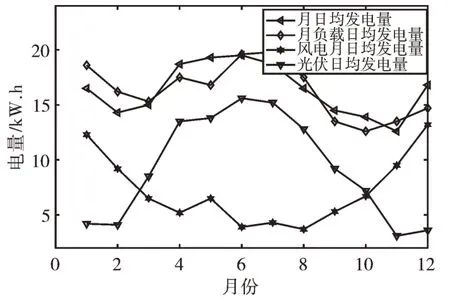
Fig.4 Generation curve and load curve圖4 發電曲線與負荷曲線

Table 2 Comparison of the two cases表2 兩種情況對比

由表2 可清晰看到考慮風光出力相關性的系統在成本、負荷缺電率和棄風棄光浪費方面分別減少了8.98%、1.23%和2.28%。上述數據也驗證了本文提出的計及風光出力相關性對于風光互補發電系統容量優化的重大意義，可以有效減少風機和光伏單獨出力的不確定性以及新能源損失，提高了電網對負荷的供電可靠性，同時降低了成本。

5 結語

本文采用NSGA-II 算法對風光互補發電系統進行多目標的容量優化，利用Frank Copula 函數得到該地區風光聯合概率分布，并得出該地區風機與光伏具有良好的負相關性，同時將成本、負荷缺電率、棄風棄光浪費率作為系統優化的3 個目標進行綜合考慮，得出最優的系統配置。本文提出的方法可減少風機和光伏單獨出力的不確定性以及新能源損失，提高了電網的供電可靠性。同時，驗證了該地區風光出力在一年四季具有嚴格的負相關特性，夏季光伏發電量多，風力發電量少，而冬季光伏發電量少，風力發電量增加，可以很好地進行風光互補聯合發電，減少能量損失，節約能源。

計及風光出力的聯合模型還需要繼續優化，將相關性分析應用于風光互補發電系統值得作進一步研究，有必要引入一些評價指標進一步證明模型的可靠性。