離散大系統的部分聯結不穩定性的判定

孫水玲

（廣州工商學院，廣東 廣州510850）

許多實際問題建立的系統（如工業系統、城市交通網系統、環境系統、經濟系統、社會系統等）往往變量很多，造成系統的維數很高，給系統穩定性的研究帶來很大的困難.為了解決這些問題，文獻［1］給出大系統的方法，即把復雜系統視為若干相互聯結的低階子系統相互作用的動態大系統，然后通過子系統及其關聯性質，給出大系統的穩定性的研究.關于這方面的研究結果已有很多.但對于一個已經建立了數學模型的大型動力系統，雖然考慮了各子系統間的關聯，然而它們關聯的強度可能會有很大的不同，而且一組子系統可能暫時與其他子系統分離也會導致大系統結構上的變化，為此文獻［1］提出了一套關聯穩定性理論.由于有些大系統中部分關聯固定，而只有部分關聯可以變化，因此文獻［2］給出部分關聯穩定性概念，文獻［3-7］給出了離散大系統的部分關聯穩定性的一些研究結果.本文主要利用向量李雅普諾夫函數法及比較原理，討論非線性離散大系統和常系數線性離散大系統的部分聯結不穩定性，給出了部分關聯不穩定性的充分條件.

1 主要結果

首先考慮具有r個子系統的n階非線性離散大系統：

其中：

證明 取大系統（1）的向量李雅普諾夫函數：

得到：

即有：

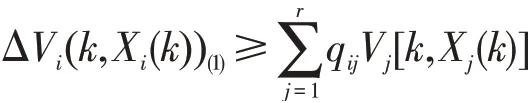
同樣有：

考慮具有r個子系統的n階線性定常離散大系統.

其中，Ai為ni×ni階常數矩陣，Aij為ni×nj階常數矩陣，它表示系統j對系統i的作用（i,j=1,2,…,r,j≠i）.Xi=(x1(i),x(

2i),…,xn(ii))T為ni維狀態分量，而且n1+n2+…+nr=n.X=(X1,X2,…,Xr)T為n維狀態向量.

系統（5）的孤立子系統為：

以下假設離散大系統（6）的每個子系統，都存在ni×ni階負定對稱矩陣Bi和常數μi使負定函數

滿足：

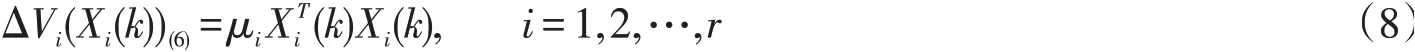
所以，

2 結論

本文中的關聯矩陣E隨著時間k變化時，定理仍然成立，而且關聯因子eij可以取［0，1］上的任何數值，即定理適用于關聯因子隨時間是變化的情況.