三角代數上的Jordan零點高階ξ-Lie可導映射

柳 靜, 張建華

(陜西師范大學 數學與信息科學學院, 西安 710119)

則{φn}n∈是一個高階導子, 其中[U,V]ξ=UV-ξVU為ξ-Lie積, U°V=UV+VU為Jordan積. 并得到套代數上Jordan零點高階ξ-Lie可導映射的具體形式.

1 引言與預備知識

設A是數域F上含單位元的代數,U,V∈A. 給定ξ,ζ∈F, 稱[U,V]ξ=UV-ξVU和U°V=UV+VU分別為U和V的ξ-Lie積與Jordan積. 設φ: A→A是線性映射, {φn}n∈: A→A是一列線性映射(φ0=idA為恒等映射). 如果對任意U,V∈A及n∈, 有

則稱{φn}n∈是A上的高階導子. 如果對任意U,V∈A, 有

φ([U,V]ξ)=[φ(U),V]ξ+[U,φ(V)]ξ,

(1)

則稱φ是A上的ξ-Lie導子. 如果對任意U,V∈A且[U,V]ζ=0有式(1), 則稱φ是A上的ζ-Lie零點ξ-Lie可導映射. 特別地, 當ζ=-1,0,1時,ζ-Lie零點ξ-Lie可導映射分別為Jordan零點ξ-Lie可導映射、 零點ξ-Lie可導映射、 Lie零點ξ-Lie可導映射. 如果對任意U,V∈A及n∈, 有

(2)

則稱{φn}n∈是A上的高階ξ-Lie導子. 如果對任意U,V∈A及n∈且U°V=0有式(2), 則稱{φn}n∈是A上的Jordan零點高階ξ-Lie可導映射.

目前, 關于算子代數上滿足某種條件的可導映射和高階可導映射的研究已得到廣泛關注, 并取得許多成果[1-10]. 例如: 文獻[1]證明了三角代數上互逆元處的高階ξ-Lie可導映射是高階導子; 文獻[2]研究了三角代數上Jordan積為冪等元處的高階ξ-Lie 可導映射, 并得到了套代數上該類高階ξ-Lie可導映射的具體形式; 文獻[3]刻畫了三角代數上交換零點ξ-Lie高階可導映射; 文獻[4]研究了三角代數上的Jordan零點ξ-Lie可導映射, 并給出了其結構. 基于此, 本文討論三角代數上的Jordan零點高階ξ-Lie可導映射.

設A和B是實或復數域F上含單位元的代數, M是(A,B)-忠實雙邊模. 在通常的矩陣運算下, 稱

為F上三角代數. 設U是三角代數且Z(U)表示其中心, 則由文獻[5]中性質3知

設I是U的單位元,IA和IB分別是A和B的單位元. 記

U11=P1UP1, U12=P1UP2, U22=P2UP2.

顯然, 三角代數U被分解為U=U11+U12+U22且U12是(U11,U22)-忠實雙邊模.

2 主要結果

引理1對任意n∈, 有:

1)φn(I)=P1φn(I)P1+P2φn(I)P2∈Z(U );

2) 對任意冪等元P∈U, 有Pφn(P)P=Pφn(I)=φn(I)P且(I-P)φn(P)(I-P)=0.

證明: 對任意冪等元P∈U, 由P°(I-P)=0得

對式(3)分別左乘P、 右乘P, 得

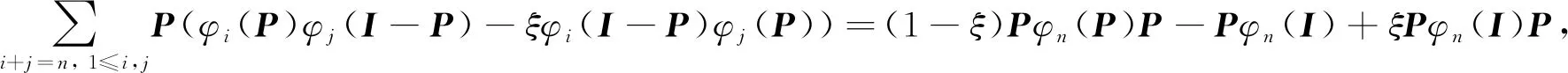
(4)

(5)

由文獻[4]中引理2.1和斷言5可知, 如果ξ≠1， 則對任意冪等元P∈U, 有

φ1(I)=P1φ1(I)P1+P2φ1(I)P2∈Z(U ),

Pφ1(P)P=Pφ1(I)=φ1(I)P,

(I-P)φ1(P)(I-P)=0.

假設當1≤k

φk(I)=P1φk(I)P1+P2φk(I)P2∈Z(U ),

Pφk(P)P=Pφk(I)=φk(I)P,

(I-P)φk(P)(I-P)=0.

則式(4)和式(5)的左邊分別為

表明式(4)和(5)左邊相等. 從而由式(4)和式(5)右邊相等及ξ≠0,1可知, 對任意冪等元P∈U, 均有

Pφn(P)P=Pφn(I)=φn(I)P.

(6)

于是

Pφn(I-P)P=0,

(7)

Pφn(I)(I-P)=0.

(8)

在式(7)中用I-P替換P, 則對任意冪等元P∈U, 有

(I-P)φn(P)(I-P)=0.

在式(8)中取P=P1, 則P1φn(I)P2=0, 從而

φn(I)=P1φn(I)P1+P2φn(I)P2.

(9)

對任意U12∈U12, 顯然P1+U12是U中的冪等元, 從而由式(6)得

(P1+U12)φn(I)=φn(I)(P1+U12),

φn(I)P1=P1φn(I).

于是對任意U12∈U12, 有U12φn(I)=φn(I)U12. 又由式(9), 有

φn(I)=P1φn(I)P1+P2φn(I)P2∈Z(U).

證畢.

引理2對任意n≥1, 有

φn(U12) ?U12,φn(P1),φn(P2)∈U12,φn(I)=0.

證明: 由文獻[4]中斷言7知,

φ1(U12)?U12,φ1(P1),φ1(P2)∈U12,φ1(I)=0.

假設當1≤k

對式(10)分別左右兩邊同乘P1和P2, 并由ξ≠0及U的2-無擾性, 可得

P1φn(U12)P1=P2φn(U12)P2=0.

表明φn(U12)?U12. 對式(10)左乘P1、 右乘P2, 并由ξ≠-1及引理1可得

φn(I)U12=U12φn(I)=0.

于是P1φn(I)P1=P2φn(I)P2=0, 從而由引理1得

φn(I)=0,P1φn(P1)P1=P2φn(P1)P2=0.

因此φn(P1),φn(P2)∈U12. 證畢.

引理3對任意n≥1, 有

φn(U11)?U11+U12,φn(U22)?U12+U22.

證明: 由文獻[4]中斷言8知, 當n=1時,φ1在U上是導子, 從而φ1(U11)?U11+U12. 假設當1≤k

對任意U11∈U11, 因為P2°U11=0, 所以由歸納假設可得

又因為ξ≠1, 于是P2φn(U11)P2=0. 因此φn(U11)?U11+U12.

同理, 對任意U22∈U22, 有φn(U22)?U12+U22. 證畢.

引理4對任意n∈,U11∈U11,U22∈U22, 有

證明: 由于U11°U22=0, 由引理3有

引理5對任意n∈,U11∈U11,V12,U12∈U12,V22∈U22, 有:

證明: 1) 由于(U11-U11V12)°(V12+P2)=0, 由引理2～引理4得

從而

2) 同理, 由(U12+P1)°(V22-U12V22)=0及引理2～引理4可得

證畢.

引理6對任意U11,V11∈U11,V12∈U12,U22,V22∈U22, 有：

由引理5中1)及歸納假設知, 一方面有

另一方面, 有

比較式(11)和式(12), 得

進而由U12的忠實性, 得

(13)

下面證明

對任意U11∈U11, 由于U11°P2=0, 由引理2和引理3可得

從而可得

(14)

同理, 對任意U22∈U22, 有

(15)

再由引理3、 式(14)及歸納假設知, 對任意U11,V11∈U11, 有

因此可得

(16)

進而由式(13),(16)及引理3有

2) 同理, 對任意U22,V22∈U22, 有

證畢.

定理1設U=Tri(A,M,B)是一個2-無擾的三角代數, {φn}n∈是U上的Jordan零點高階ξ-Lie可導映射(ξ≠0,±1), 則{φn}n∈是U上的高階導子.

證明: 對任意U,V∈U, 有U=U11+U12+U22,V=V11+V12+V22, 其中Uij,Vij∈Uij(1≤i≤j≤2). 于是, 由引理2～引理6得

即{φn}n∈是U上的高階導子. 證畢.

設H是實或復數域F上的Hilbert空間, B(H )表示H上的全體有界線性算子, H上的套N是一簇包含H和{0}的全序閉子空間, 且在任意交和任意閉線性張運算下封閉, 套N相應的套代數為Alg N ={T∈B(H ):TN?N, ?N∈N }. 由定理1, 有如下結論:

推論1設N是Hilbert空間H上的一個非平凡套, Alg N是相應的套代數, {φn}n∈是Alg N上的Jordan零點高階ξ-Lie可導映射(ξ≠0,±1), 則{φn}n∈是Alg N上的高階導子.