地類圖斑與多源在線地圖坐標粗匹配研究

黃亮平，李德平,2*，周 亮,2，劉師師

（1.湖南師范大學 資源與環境科學學院，湖南 長沙 410081；2.湖南師范大學地理空間大數據挖掘與應用湖南省重點實驗室，湖南 長沙 410081）

地類圖斑與多源在線地圖集成不僅可以促進地類圖斑和多源在線地圖資源的社會化應用，還可為政府相關部門和社會大眾提供一種獲取地類圖斑與多源在線地圖集成信息的手段。本文采用的地類圖斑數據來源于某地區第三次土地調查數據庫，多源在線地圖以天地圖、百度地圖、Google Earth為例，分別將地類圖斑與這3種在線地圖進行集成。在集成過程中，由于地類圖斑的坐標系為CGCS2000高斯投影坐標系，而天地圖為CGCS2000坐標系、百度地圖為百度坐標系（BD09）、Google Earth為1984世界大地坐標系（WGS84），因此需進行坐標匹配。本文研究的是坐標粗匹配，誤差控制在10 m以內即可。

目前針對CGCS2000高斯投影坐標與CGCS2000坐標、BD09坐標、WGS84坐標的匹配均有研究。對于投影坐標與地理坐標的轉換問題，無論是CGCS2000、WGS84、西安1980還是北京1954，均可利用高斯反算公式進行坐標轉換，得到的坐標精度不低于0.0001″，雖然存在一定的誤差，但能滿足日常生產需求[1-5]。CGCS2000坐標與BD09坐標之間的轉換，可利用多項式變換模型進行分區坐標轉換，區域大小基本一致的坐標轉換精度也基本一致[6]。對于百度地圖坐標（BD09II）與WGS84坐標存在較大偏移，且BD09II坐標無法轉換為WGS84坐標的現象，利用坐標轉換算法可實現WGS84、GCJ02和BD09三種坐標之間的相互轉換[7-8]；利用百度地圖API或依托控制點庫進行離線轉換可實現WGS84坐標到BD09坐標的轉換[9-10]。BD09坐標向WGS84坐標的轉換方式主要包括二階差分公式法、等量偏移法、格網法以及BP神經網絡法[7,11]。對于CGCS2000坐標與WGS84坐標之間的轉換，若需精確轉換，目前推薦從政府部門和CORS服務中實現[12]。CGCS2000坐標與WGS84坐標的轉換需明確所對應的歷元和框架，可根據具體精度要求，分別利用歷元轉換、框架轉換、布爾莎七參數模型或結合使用進行坐標轉換[12-14]。歷元轉換影響遠大于框架轉換，歷元引起的坐標差別可達dm級甚至m級，而框架引起的坐標差別僅為cm級[12-13]，因此進行框架轉換時，必須先統一歷元[13]，當精度要求為cm級時，只需進行歷元轉換[13]。CGCS2000坐標系與WGS84坐標系因扁率的差別不會影響某點的經度，對緯度和高度的影響則與該點的緯度有關，且最大差值遠小于1 mm，在目前坐標系的實現精度范圍內是可以忽略的[12,15-16]，因此當精度要求為cm級及以上時，認為CGCS2000坐標系和WGS84坐標系是基本相容的[12-13,16]。

1 地類圖斑與3種在線地圖的坐標系

地類圖斑為CGCS2000高斯投影坐標系，按3°分帶投影，位于37帶內，中央子午線為111°；天地圖為CGCS2000坐標系，百度地圖為BD09坐標系，Google Earth為WGS84坐標系。CGCS2000坐標系是我國目前最新的國家大地坐標系，是一種地心坐標系，即坐標系原點為地球質心。我國自2008年7月1日起，全面啟用CGCS2000坐標系，國家測繪局授權組織實施[15]。CGCS2000高斯投影坐標系是基于CGCS2000坐標系利用高斯投影方法進行投影得到的投影坐標系。WGS84坐標系是美國國防部制圖局建立的坐標系，是國際上采用的一種地心坐標系，WGS84坐標系與CGCS2000坐標系橢球參數僅在扁率上略有差別[16-17]。BD09坐標系是在WGS84坐標系的基礎上經過兩次加密而得到的，第一次是從WGS84坐標系加密為火星坐標系（CGJ02），第二次是從GCJ02坐標系加密為BD09坐標系，且不同區域加密算法不一樣[6]。

2 地類圖斑與3種在線地圖坐標粗匹配方法

2.1 地類圖斑與天地圖坐標粗匹配方法

2.1.1 CGCS2000坐標系的橢球參數

CGCS2000坐標系的橢球參數主要包括長半軸、短半軸、扁率、第一偏心率平方和第二偏心率平方，如表1所示。

表1 CGCS2000坐標系的橢球參數

2.1.2 高斯反算

高斯平面坐標(x,y)向大地坐標(L,B)轉換的過程稱為高斯反算，計算公式為[1]：

2.2 地類圖斑與百度地圖坐標粗匹配方法

地類圖斑采用CGCS2000參考橢球，百度地圖采用WGS84參考橢球，且在WGS84的基礎上經過了兩次加密。雖然可利用嚴密的坐標轉換公式將CGCS2000參考橢球轉換為WGS84參考橢球，再利用百度地圖API、坐標轉換算法或依托控制點庫進行離線轉換，將WGS84坐標轉換為BD09坐標；但該方式比較復雜、需要控制點、百度地圖API，一次只能轉換100個點且不可逆。由于百度地圖在不同區域采用不同的加密算法，且多項式變換模型階數越高、校正變形越復雜、非控制點轉換誤差越顯著，因此不宜采用三階以上的多項式變換模型進行坐標變換[18]。本文試圖利用不同大小的格網，結合平均位移法（零階多項式）、一階多項式、二階多項式、三階多項式以及平面四參數法對兩套坐標系之間的匹配關系進行對比研究，如圖1所示。

圖1 地類圖斑與百度地圖坐標粗匹配技術流程圖

2.2.1 坐標匹配方法

本文分別采用平均位移法、一階多項式、二階多項式、三階多項式和平面四參數法進行對比研究，從而挑選出最適合本文的方法。5種方法的適用情況、需求參數個數、需要的最少非相關公共點數如表2所示，可以看出，除平均位移法外，其他方法若公共點個數大于最少非相關公共點數，則可利用最小二乘法求解。

表2 不同坐標匹配方法的適用特征

設任意一點A在地類圖斑中的坐標為(x,y)，利用坐標匹配方法轉換后的坐標為(x′,y′)，在百度地圖中對應的真實坐標為(X,Y)。

1）平均位移法的數學模型為：

式中，Δx、Δy分別為x和y方向的平均位移量。

2）一階多項式的數學模型為：

3）二階多項式的數學模型為：

4）三階多項式的數學模型為：

5）平面四參數法的數學模型為：

式中，Δx和Δy分別為x和y方向的平移參數；m為尺度參數；α為旋轉參數。

2.2.2 精度評定標準

通過比較檢驗點預測值與真實值之間的均方根誤差（RMSE）得到坐標匹配方法的精度。

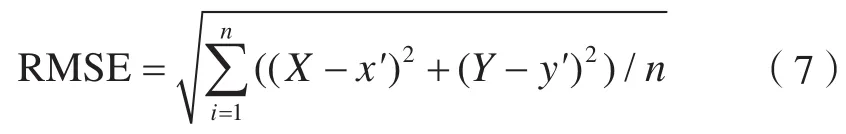
式中，n為檢驗點個數。

2.3 地類圖斑與Google Earth坐標粗匹配方法

為了驗證在本文精度條件下地類圖斑坐標與Google Earth坐標基本相容，獲取了大量地類圖斑與Google Earth相同位置特征點的坐標，再分別計算X方向和Y方向的差值進行驗證，如圖2所示。

圖2 地類圖斑與Google Earth坐標粗匹配技術流程圖

3 地類圖斑與3種在線地圖坐標粗匹配過程

3.1 地類圖斑與天地圖坐標粗匹配

地類圖斑為CGCS2000高斯投影坐標系，天地圖為CGCS2000坐標系，因此基于CGCS2000坐標系橢球參數，利用高斯反算方法，將地類圖斑的高斯投影坐標系轉換為CGCS2000坐標系，即可進行地類圖斑與天地圖的坐標粗匹配。

3.2 地類圖斑與百度地圖坐標粗匹配

為了比較不同格網劃分和不同坐標匹配方法對坐標匹配精度的影響，以便挑選出最適合的格網大小和坐標匹配方法，本文以某地區第三次土地調查數據庫中的地類圖斑為實驗區，面積約為1 549 km2（未分區），首先在ArcGIS中依次添加20×20 km（2×2分區）、10×10 km（4×4 分區）、5×5 km（8×8分區）、2.5×2.5 km（16×16分區）的格網；再按“分布均勻，邊界、四角有點”的原則[19]，分別利用ArcGIS和百度地圖拾取坐標系統獲取地類圖斑和百度地圖相同位置特征點的坐標（16對公共點、10對檢驗點）；然后對于每一對特征點，設置地類圖斑平面坐標為(X地,Y地)，百度地圖地理坐標為(L百,B百)，利用ArcGIS將百度地圖地理坐標進行3°帶高斯37帶投影，得到平面坐標(X百,Y百)，并將地類圖斑平面坐標與百度地圖平面坐標整理成一個表格文件（表3）；最后分別采用平均位移法、一階多項式、二階多項式、三階多項式、平面四參數法對16對公共點坐標進行參數計算，得到轉換參數，基于轉換參數利用10對檢驗點坐標進行坐標匹配，并進行精度評定。

表3 地類圖斑與百度地圖相同位置特征點的平面坐標/m

3.3 地類圖斑與Google Earth坐標粗匹配

地類圖斑為CGCS2000高斯投影坐標系，Google Earth為WGS84坐標系，分別利用ArcGIS和Google Earth客戶端獲取地類圖斑和Google Earth相同位置的425對特征點坐標。對于每一對特征點，設置地類圖斑平面坐標為(X地,Y地)，Google Earth地理坐標為（L谷,B谷)，利用ArcGIS將Google Earth地理坐標進行3°帶高斯37帶投影，得到平面坐標(X谷,Y谷)，并將地類圖斑平面坐標與Google Earth平面坐標整理成一個表格文件（表4）。基于此，分別計算X和Y方向差值，得到其散點圖（圖3、4）。

表4 地類圖斑與Google Earth相同位置特征點平面坐標/m

4 匹配結果與分析

4.1 地類圖斑與天地圖坐標粗匹配結果

對于地類圖斑與天地圖坐標的粗匹配，地類圖斑與天地圖均采用CGCS2000參考橢球，只是地類圖斑為投影坐標系，而天地圖為大地坐標系。因此，只需利用高斯反算就能實現地類圖斑與天地圖的坐標粗匹配，且坐標精度不低于0.000 1″，符合本文坐標粗匹配精度要求。

4.2 地類圖斑與百度地圖坐標粗匹配結果

對于地類圖斑與百度地圖坐標的粗匹配，針對不同格網分區，本文分別利用5種方法對地類圖斑與百度地圖的坐標匹配關系進行了對比研究，得到不同分區不同方法坐標匹配的RMSE（表5）。

表5 不同分區不同方法坐標匹配的RMSE/m

由表5可知，無論利用哪種方法，區域越小，則RMSE越小；在所有分區中，利用二階多項式得到的RMSE最小；當區域較大時（未分區、2×2分區），利用5種方法得到的RMSE基本上一致，考慮到方法的簡便性，宜選用平均位移法；當區域較小時（4×4分區、8×8分區、16×16分區），二階多項式優于其他方法，因此宜選用二階多項式方法。本文研究地類圖斑與百度地圖坐標的粗匹配，精度要求控制在10 m以內，同時考慮到區域越小帶來的計算量越大，因此宜選用8×8分區格網結合二階多項式方法進行坐標匹配。

4.3 地類圖斑與Google Earth坐標粗匹配結果

對于地類圖斑與Google Earth坐標的粗匹配，由圖3、4可知，地類圖斑與Google Earth在X、Y方向的差值范圍約為(-6,10)和(-10,10)，符合本文坐標粗匹配精度要求，因此可將CGCS2000坐標系與WGS84坐標系當成同一坐標系看待。同時，在精度要求為cm級及以上時，可認為CGCS2000坐標與WGS84坐標基本一致[13]。

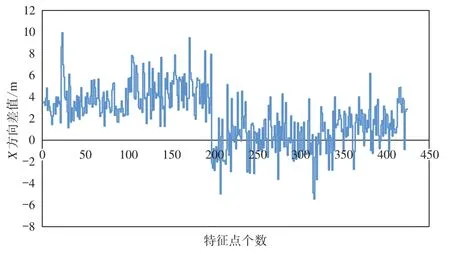
圖3 地類圖斑與Google Earth在X方向的差值圖

圖4 地類圖斑與Google Earth在Y方向的差值圖

5 實例驗證

以VS2013為開發平臺，以C#為編程語言，本文首先利用FME API獲取地類圖斑的空間信息，將Web Browser控件嵌入HTML，并在HTML中分別利用各自地圖API調用3種在線地圖；再將地類圖斑以覆蓋物的形式分別疊加在3種在線地圖上，實現地類圖斑與3種在線地圖的集成；然后利用CGCS2000參考橢球參數進行高斯反算實現地類圖斑與天地圖的坐標粗匹配；最后利用8×8分區格網結合二階多項式方法將地類圖斑轉換為百度地圖平面坐標，由于百度地圖為地理坐標，因此還需利用WGS84參考橢球參數進行高斯反算才能實現地類圖斑與百度地圖的坐標粗匹配。由于本文的精度要求在m級，CGCS2000坐標系與WGS84坐標系可通用，因此只需利用CGCS2000參考橢球參數將地類圖斑進行高斯反算即可與Google Earth相匹配。

地類圖斑與3種在線地圖能很好地進行坐標粗匹配（圖5），規避了傳統地理信息保密性、參數保密性以及坐標精匹配。由圖5可知，本文選用的8×8分區格網結合二階多項式方法可較好地解決地類圖斑與百度地圖集成時出現的坐標匹配問題，是一種更簡單、快速、直觀的適用于普通社會大眾的坐標粗匹配途徑。

圖5 地類圖斑與天地圖、百度地圖、Google Earth坐標粗匹配示例

6 結 語

針對地類圖斑與多源在線地圖集成時出現的坐標不匹配問題，以天地圖、百度地圖、Google Earth為例，對地類圖斑與3種在線地圖的坐標匹配進行了研究，并通過實例對坐標匹配結果進行了驗證。

1）對于采用同一參考橢球的地類圖斑與天地圖，利用高斯反算方法即可實現二者的粗匹配，坐標精度不低于0.000 1″。

2）對于地類圖斑與百度地圖的粗匹配，通過對比不同格網大小和不同方法對地類圖斑與百度地圖坐標匹配精度的影響發現，格網越小，坐標匹配精度越高。在5種方法中，二階多項式方法的效果最好。區域較大時，宜選用平均位移法；區域較小時，宜選用二階多項式方法；但實際應用時，可根據具體情況選擇，應同時考慮精度與計算量，本文中宜選用8×8分區格網結合二階多項式方法實現地類圖斑與百度地圖的粗匹配。

3）對于地類圖斑與Google Earth坐標的粗匹配，本文驗證了在精度要求為m級時，CGCS2000坐標系和WGS84坐標系可視為同一坐標系。