基于多影響因素建立鋰離子電池充電內阻的動態模型

潘海鴻 張 沫 王惠民 馮 喆 陳 琳,2

基于多影響因素建立鋰離子電池充電內阻的動態模型

潘海鴻1張 沫1王惠民1馮 喆1陳 琳1,2

（1. 廣西大學機械工程學院 南寧 530004 2. 廣西電化學能源材料重點實驗室培育基地可再生能源材料協同創新中心 南寧 530004）

鋰離子電池內阻建模對研究電池熱管理具有重要意義。充電內阻受溫度、充電倍率等眾多因素的影響，該文分析電池的內阻變化特性與多種影響因素（充電倍率、荷電狀態以及溫度）之間的關系，采用最小二乘法的二元多項式和三次樣條插值算法對不同充電倍率、荷電狀態以及溫度下的電池充電內阻進行建模，并采用所建立的多因素動態內阻模型對不同狀態下的充電內阻進行估算。實驗結果表明，所建立的動態內阻模型獲得的內阻估算值與實驗值的最大誤差不超過6mW，證明所提出的電池充電內阻建模方法的有效性。

充電內阻 多因素 內阻模型 最小二乘 二元多項式 三次樣條

0 引言

鋰離子電池作為電動汽車的主要儲能裝置，是電動汽車的重要組成部分[1-4]。電動汽車的儲能裝置由上千個鋰離子電池單體組成，在大電流快速充電過程中電池會釋放出大量的熱量，電池組積聚熱量導致電池外部工作環境溫度過高，這將會加速電池性能衰退，甚至引發“熱失控”現象[5-6]。電池充電內阻是電池在充電工作時影響產熱量大小的關鍵參數，對電池充電內阻準確建模能為電動汽車的安全性和熱管理系統提供有效的決策參考[7]。

國內外學者對鋰離子電池充電內阻研究主要集中在充電內阻影響因素與充電內阻模型兩方面，采用充電脈沖電流電壓的變化或等效電路模型來描述電池特性并獲取充電內阻[8]。林春景等采用混合脈沖功率特性法對不同溫度區間下的內阻進行實驗分析，驗證電池阻抗對荷電狀態（State of Charge, SOC）和溫度的依賴關系[9]。B. V. Ratnakumar等采用直流阻抗法分別對鋰離子電池在25℃、0℃及-20℃不同SOC和充放電倍率下的內阻進行測試，并對溫度、SOC及倍率進行分析研究，獲取內阻關于溫度的阿倫尼烏斯圖[10]。Liu Xingtao等對不同溫度和SOC下內阻進行測試，詳細描述了電池內阻、SOC和溫度之間的關系，建立了基于溫度的一元三次多項式模型[11]。W. Wang等采用電化學阻抗譜（Electrochemical Impedance Spectroscopy, EIS）和電流脈沖技術對新舊狀態下的電池阻抗特性進行全面的描述，明確指出，電池的阻抗特性在很大程度上取決于電池的狀態，如SOC、溫度及電流，并基于阿倫尼烏斯方程給出一個溫度-內阻模型[12]。姜久春等測試了磷酸鐵鋰電池在充放電條件下的阻抗特性，并進行了實驗研究，得到不同SOC下的阻抗譜，獲得的阻抗譜曲線能以特高精度測量電荷轉移阻抗和擴散阻抗，很好地驗證了鋰離子質量分數、電極材料的電化學特性所引起的電極極化和濃差極化的顯著變化[13]。對基于阿倫尼烏斯方程10%SOC、50%SOC和90%SOC下的電荷轉移阻抗特性進行了分析，表明電池阻抗與溫度、SOC及充放電倍率存在著直接關系?？傮w而言，現有的多數方法多側重于通過算法改進或融合來描述各個因素（溫度、SOC及放電倍率）與內阻的獨立建模，雖然有重要的研究價值，但在實際情況下電池內阻建模需要整合所有的影響因素進行準確的建模。

由于實際情況中電池充電倍率、溫度及SOC對電池充電內阻均有影響[14]，只考慮一種或兩種因素建模會導致構建模型誤差較大，而如何從在線可測量參數（溫度、SOC及充電倍率）中尋求與內阻的整體關聯，并基于構建電池多因素動態內阻模型進行內阻的準確估算是電池熱管理系統亟待解決的問題。針對此問題，提出融合充電倍率、溫度以及SOC三個因素的動態內阻模型。采用18650車用動力三元鋰離子電池作為研究對象，對不同充放電倍率、溫度及SOC下的充電內阻進行測試并對其特性進行分析，最終，以上述三個因素為自變量、內阻為因變量，構建多因素動態充電內阻模型，從而避免了對電池進行測量實現對充電內阻的在線估算，為電池熱管理系統提供理論基礎。

1 多因素動態充電內阻模型建立方法

電池充電內阻受溫度、SOC和充電倍率的影響，采用最小二乘法的二元多項式擬合構建內阻關于和SOC的函數關系，得到內阻關于和SOC擬合的二元多項式函數系數。引進三次樣條插值算法將充電倍率與二元多項式系數建立函數關系，構建以、SOC及充電倍率三個因素為自變量、內阻為因變量的多因素動態充電內阻模型。多因素動態內阻模型構建流程如圖1所示，具體步驟如下：

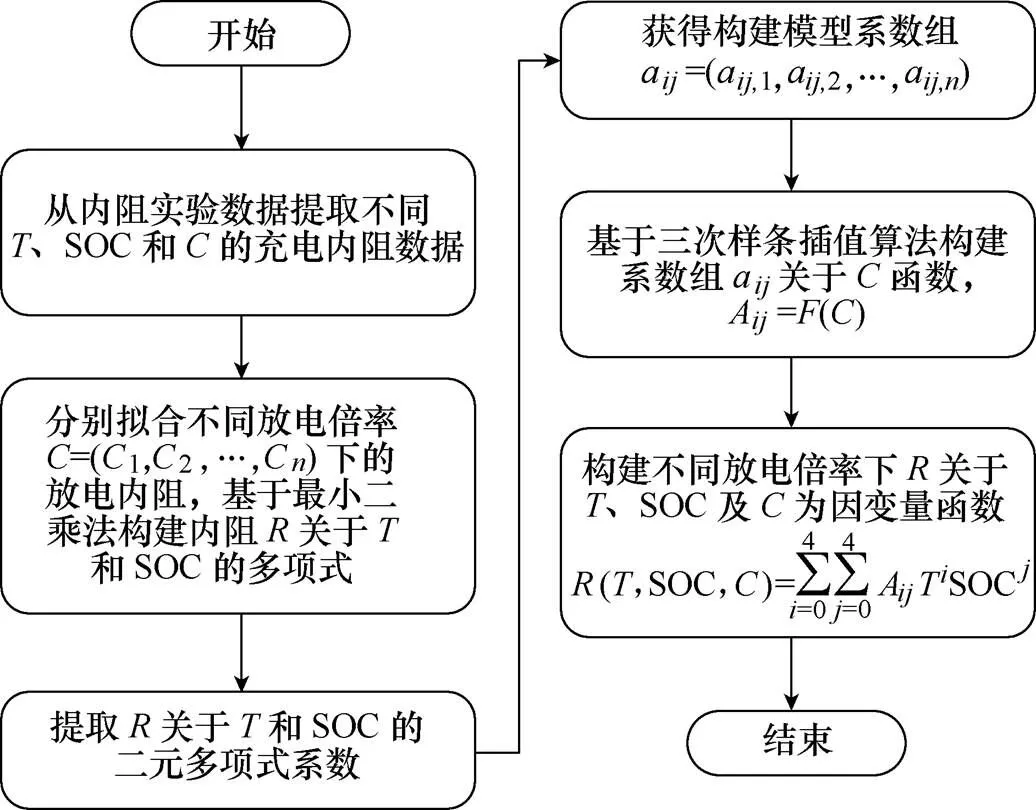
圖1 多因素動態內阻模型構建流程

（1）根據實驗記錄的電池數據計算充電內阻。

（2）建立關于和SOC的函數擬合，對給定充電倍率下的內阻均可由和SOC唯一確定，采用最小二乘法的二元多項式函數擬合因變量與自變量和SOC之間函數關系，此處選二元多項式的階數為4階。該擬合方法拓展到其他充電倍率下的擬合為

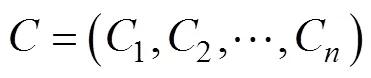
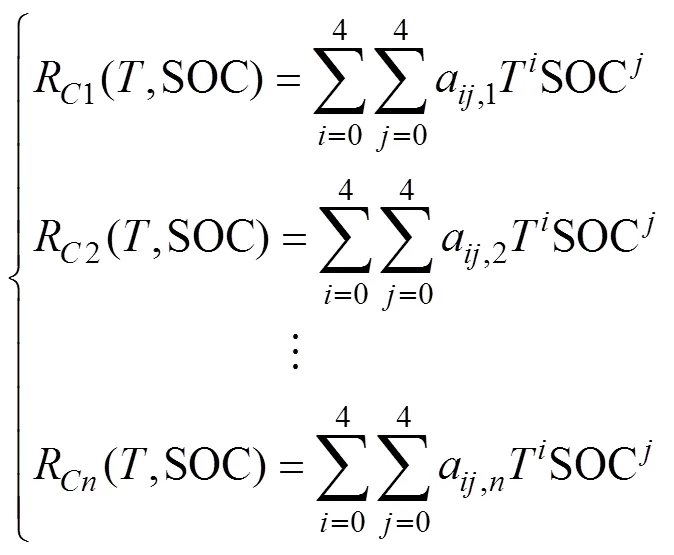
（3）分別提取不同充電倍率下的關于和SOC擬合的二元多項式函數系數組為

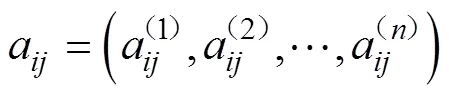
（4）為了尋求a與充電倍率之間內在的函數關系，將第（3）步提取的不同充電倍率下的二元多項式函數系數組a，基于三次樣條插值法在倍率數組區間上取1個節點，分割成段；并將每一段倍率數據點之間進行分段，構建出一個三次樣條函數；最后得到一個整體連續的關于以充電倍率為自變量的三次樣條插值函數為

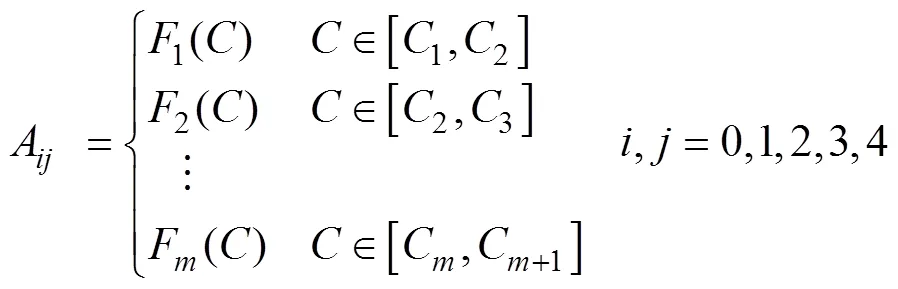
（5）將式（4）代入式（2）中獲得以充電倍率為自變量、關于和SOC二元多項式函數的系數為因變量的函數關系，即構建關于、SOC和充電倍率的多因素動態充電內阻模型為

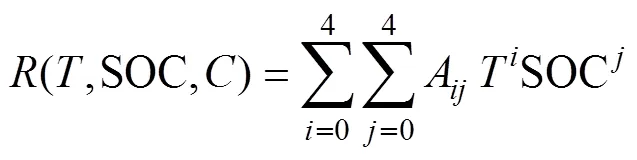
2 實驗

2.1 實驗設備

實驗測試平臺由電池充放電系統、恒溫箱和鋰離子電池三部分組成。充放電系統主要包括直流電源、電子負載儀和上位機等，充放電系統設備精度，主要參數見表1；恒溫箱用于控制電池實驗的環境溫度，其溫度的測量誤差值小于±0.5℃，測試電池為某商業18650車用動力三元鋰離子電池，具體參數見表2。

表1 直流電源及電子負載儀主要參數

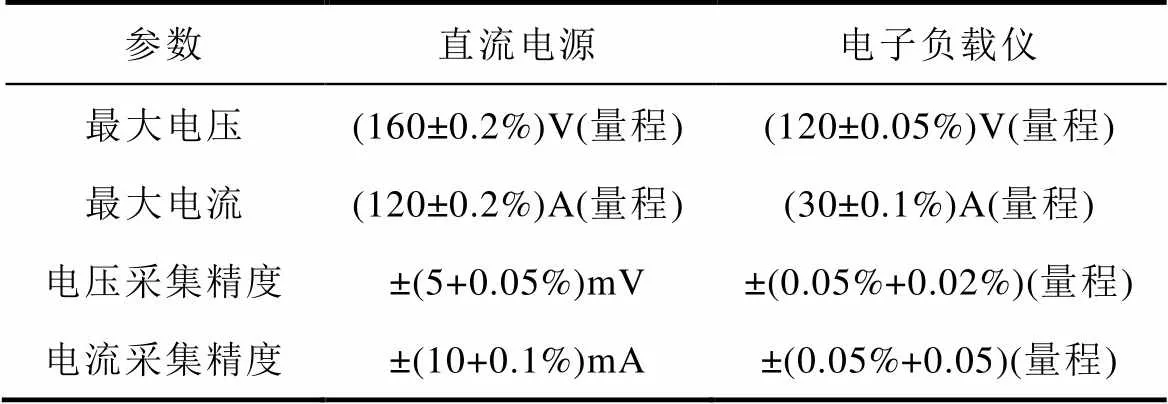
Tab.1 Main parameters of DC power supply and electronic load meter

表2 電池參數

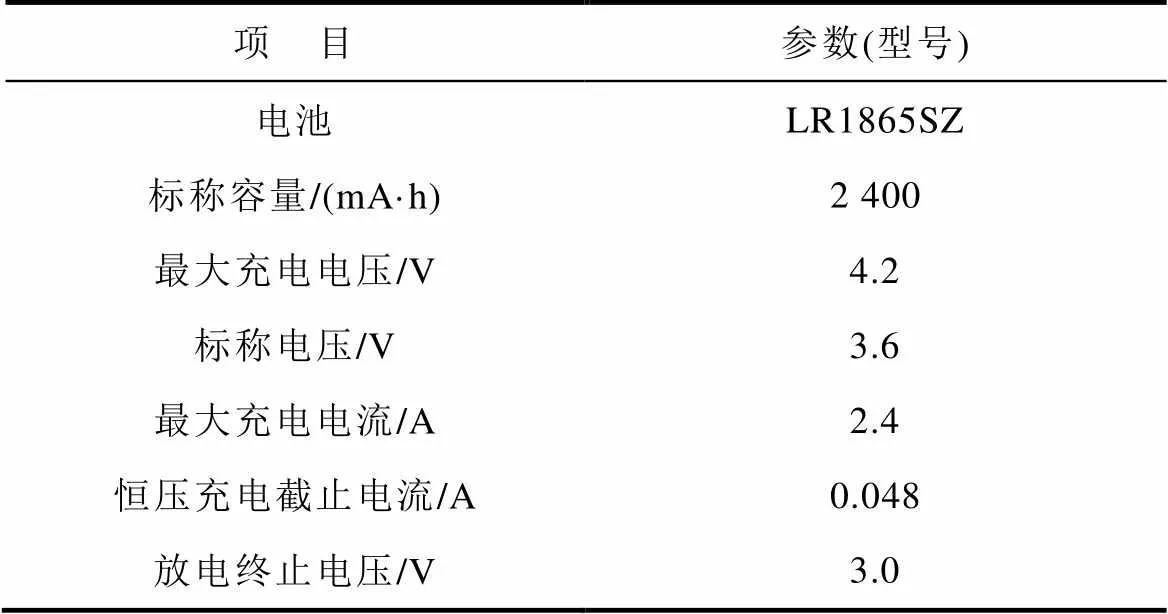
Tab.2 Battery parameters

2.2 實驗步驟

鑒于國內外相關標準中規定的電池內阻測試方法時間成本高，實驗測試采用本課題組提出的Multi- rate HPPC法測量電池的充電內阻[15]。Multi-rate HPPC電壓電流波形如圖2所示。該方法在完成每個充放電脈沖測試后增加一個容量補損的回充階段，避免傳統HPPC法充放電脈沖過程中容量的損失，既能對每一階段電池的SOC精確計算，又能完成多個倍率的充放電脈沖測試實驗。

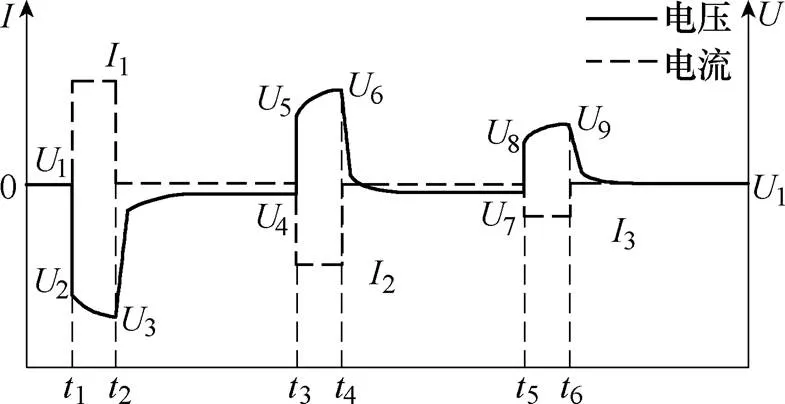
圖2 Multi-rate HPPC電壓電流波形

實驗測試電池在多溫度（5℃、15℃、25℃、35℃、45℃）、不同SOC及多種充電倍率下的充電內阻特性變化，步驟如下：

（1）將電池以標準恒壓-恒流（Constant Voltage- Constant Current, CV-CC）充電直至電池滿充，計此時荷電狀態SOC為100%，并靜置1h。

（2）將電池置于恒溫箱內，并設置第一個溫度測量點為5℃，以1恒流放電至SOC減少10%，靜置1h。

（4）九種SOC狀態下的內阻測試。分別調整電池SOC至0.9、0.8、0.7、0.6、0.5、0.4、0.3、0.2、0.1，重復上述步驟（2）、步驟（3），測量出電池在這九種SOC狀態下的響應電壓數據。

（5）四種溫度點下的內阻測試。將步驟（2）中的溫度測量點依次調整為15℃、25℃、35℃和45℃，重復步驟（1）、步驟（4），分別測量出電池在這四種溫度條件下的響應電壓數據。

（6）計算充電內阻。根據步驟（1）～步驟（5）得到電池在不同溫度、不同百分比SOC及不同倍率下響應電壓數據，計算出電池在不同溫度及不同百分比SOC下的多倍率充電內阻。

3 鋰離子電池充電內阻特性分析

根據Multi-rate HPPC實驗獲取電池在不同充電倍率、溫度以及SOC下的內阻數據，從鋰離子電池在實際充電過程中電池荷電狀態、溫度和充電倍率對電池內阻的影響展開分析。

3.1 不同溫度及荷電狀態對電池內阻的影響

電池在多溫度（5℃、15℃、25℃、35℃和45℃）下充電倍率均為0.25工況時的內阻隨SOC變化的平面圖如圖3a所示，不同溫度、SOC和內阻變化的三維立體圖如圖3b所示。由圖3整體可見，電池在充電過程中，當測量電池的環境溫度逐漸升高（由5℃升到45℃）時，各個SOC狀態下的電池充電內阻均減小，即溫度與充電內阻呈明顯的負相關。在低溫（5℃）下相較于常溫（25℃）和高溫（45℃）時電池內阻隨SOC的變化波動更為明顯，呈現出典型的非線性特征。當電池的環境溫度由15℃降低到5℃時，內阻值的增長幅度要遠大于由45℃降低到35℃。電池在低SOC（0.1～0.2）時，在低溫（5℃）和高溫（45℃）下測量出來的電池內阻值相差高達近60mW，這是因為溫度通過影響鋰離子在正負極脫嵌與嵌入速度以及電解液黏度等，進而影響電池內阻的阻值[16-17]。因此，溫度是影響電池內阻的關鍵因素之一。

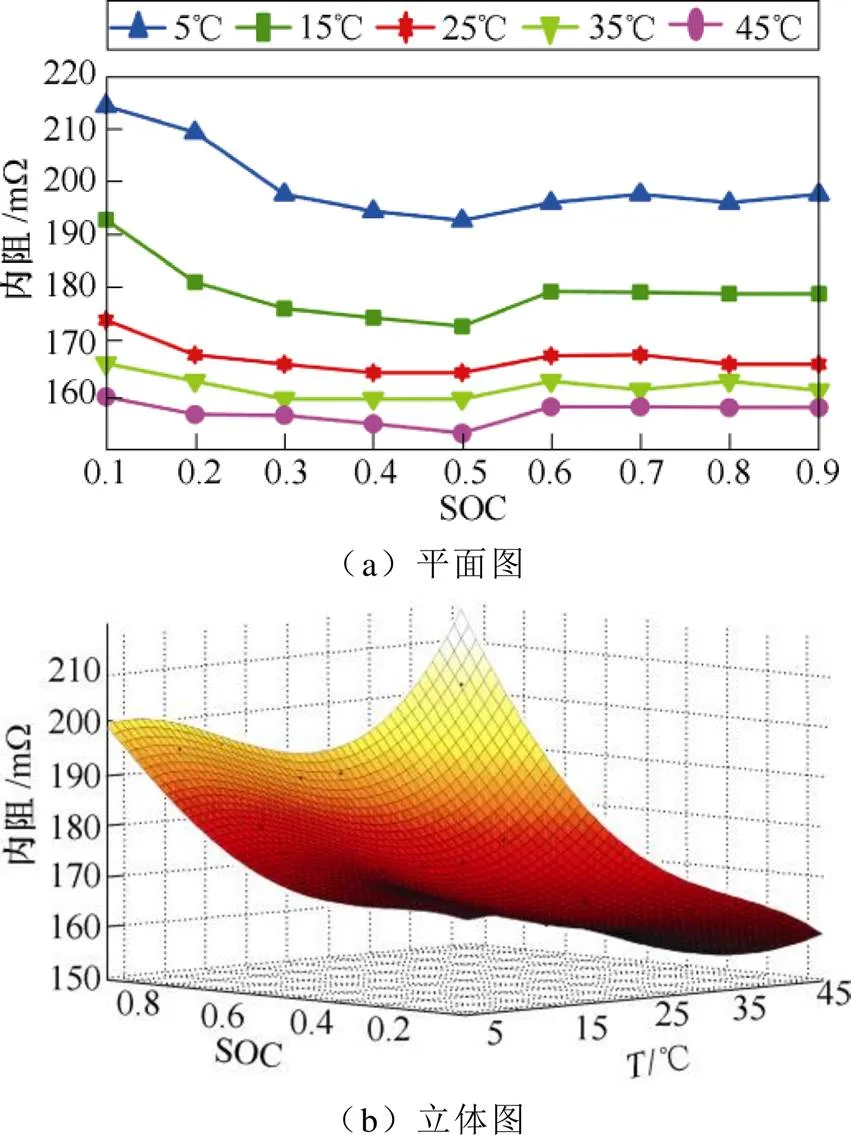
圖3 不同溫度和SOC下的充電內阻

電池在5℃和15℃下的內阻隨SOC呈現相同的變化規律（見圖3a），當SOC由0.1增大到0.5時，內阻值降低；但是，當SOC由0.5增長到0.6時，內阻值上升；SOC繼續由0.6增長到0.9時，內阻值基本不變。而在其他25℃、35℃及45℃溫度下，充電內阻隨SOC（0.1～0.9）的變化幅度很小。從高溫（45℃和35℃）、常溫（25℃）和低溫（5℃和15℃）時整體內阻值隨SOC變化曲線來看，當SOC在大于30%且小于80%范圍內時，充電內阻較?。划擲OC＜30%或SOC＞80%時，充電內阻較大。此外，不同溫度下的電池內阻隨SOC變化曲線的具體數值也存在差異。在低溫（5℃）條件下，SOC變化對電池內阻影響較大，內阻波動高達35mW，因此在進行低溫內阻建模時，應該重點考慮SOC對內阻的影響。

3.2 充電倍率對內阻的影響

選擇電池在低溫5℃、常溫25℃和高溫45℃下不同充電倍率的充電內阻進行分析，其不同充電倍率下的充電內阻如圖4所示。從圖4可知，電池在低溫（5℃）、常溫（25℃）及高溫（45℃）下，充電倍率大小對電池內阻阻值均有影響。特別在低溫下電池內阻隨著充電倍率的增加大致呈現為下降的規律，圖4a中內阻在充電倍率為0.75和0.125的變化最大為16.5mW。在常溫及高溫下，內阻隨著充電倍率的增加表現為上升趨勢，圖4b和圖4c中充電內阻在倍率為1和0.125下測量出來的內阻值分別相差近5mW和7mW。雖然充電倍率相較于和SOC對內阻的影響較小，但是，要建立準確的電池充電內阻模型，需要考慮電池充電內阻隨充電倍率的變化關系。

圖4 不同充電倍率下的充電內阻

4 多因素動態充電內阻模型的驗證與分析

根據圖1的模型構建方法，結合Multi-rate HPPC法測量的實驗數據，采用Matlab對內阻與溫度和SOC進行擬合，并提取擬合后的二元多項式函數的系數；然后，采用三次樣條插值算法構建所提取的二元多項式函數的系數與電池充電倍率的函數關系式。具體為：

（1）采用充電倍率為0.125、0.25、0.375、0.5、0.625、0.75、0.875和1下，分別構建在充電過程中的多因素動態充電內阻模型，根據式（2）分別擬合這9個倍率，因變量與自變量（5～45℃，每次間隔10℃，共5個溫度點）和SOC（0.1～0.9，每次間隔0.1，共9個SOC點）的二元四次多項式函數，并提取各倍率下的函數系數組，提取的不同充電倍率下二元四次多項式系數組a見表3。

表3 不同充電倍率下二元四次多項式系數組

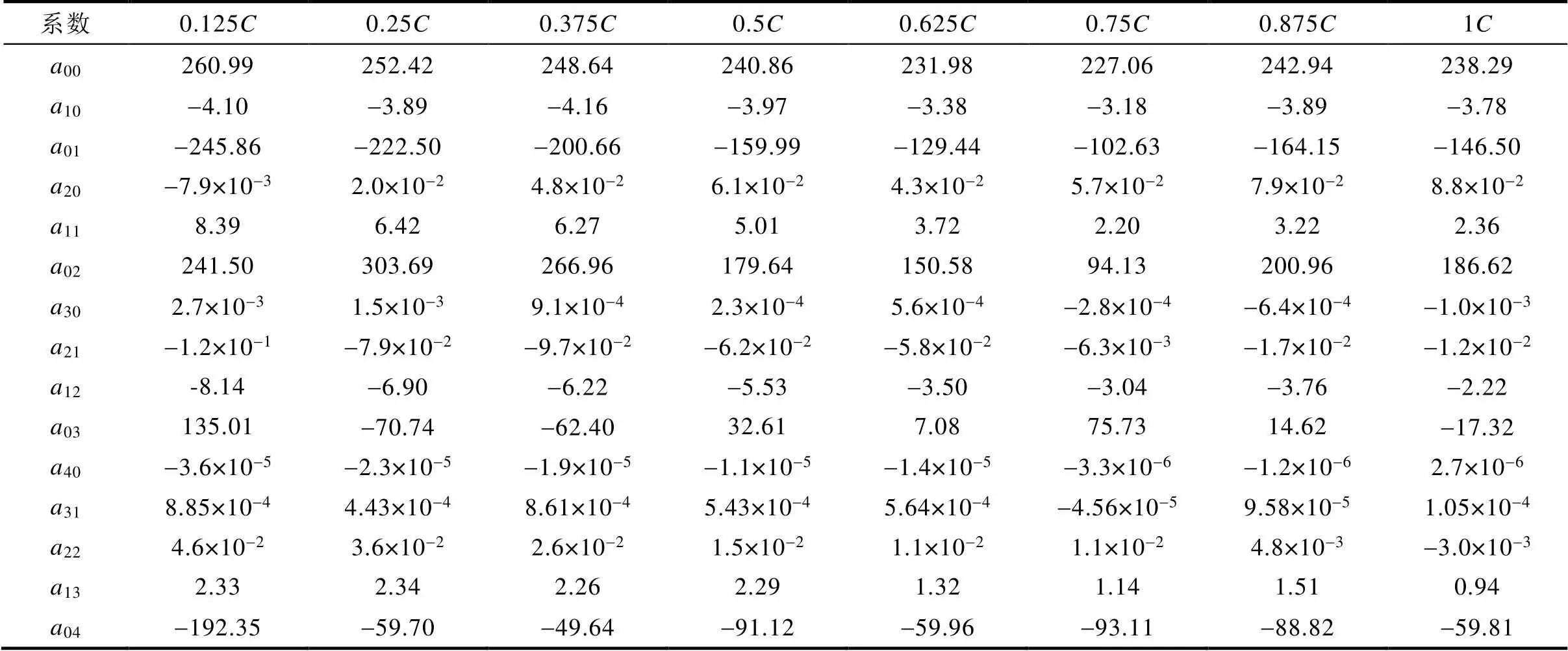
Tab.3 Binary quadric polynomial coefficient at different charging rates

（2）采用三次樣條插值法，根據式（4）將上一步中提取的各個倍率下的二元四次多項式系數組a分別擬合成關于以倍率為自變量，系數組a為因變量的三次樣條函數。表3中15個系數和倍率擬合的三次樣條函數圖像如圖5所示。在充電倍率區間[0.15, 1]內，每輸入一個倍率可以估算出一組與之對應的系數組（00～04），即可在該區間獲得其他充電倍率下的內阻關于和SOC二元四次多項式函數的系數，再由式（5）構建充電過程中關于、SOC和充電倍率的多因素動態內阻模型。

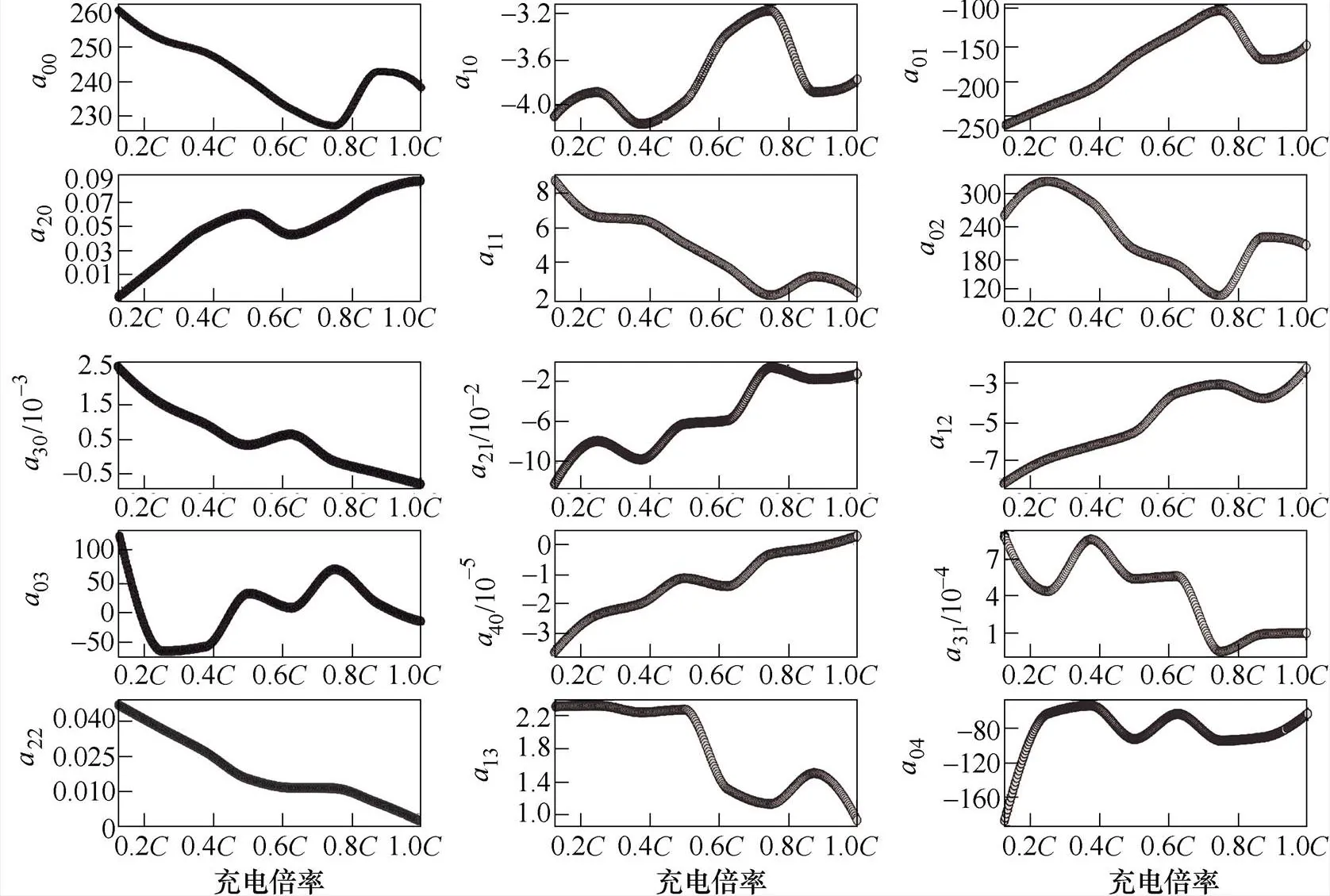
圖5 15個系數和倍率擬合的三次樣條函數圖像

為驗證模型估算的準確性，充電倍率分別選取0.187 5、0.562 5和0.937 5，溫度分別為5℃、25℃和45℃，SOC分別為0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，對充電內阻的實驗值與所建立的多因素動態內阻模型估算值進行比較如圖6所示。從圖6中可看出，內阻誤差值隨SOC的變化曲線具有相似的變化規律。通常估算內阻誤差值在低溫（5℃）和常溫（25℃）下隨SOC的波動幅度比在高溫（45℃）工況下大，且常溫內阻誤差數值大體要大于高溫的內阻誤差值，但是內阻絕對誤差的最大值卻發生在常溫下SOC=0.9時，倍率為0.937 5工況中。從具體數據來看，在0.187 5充電倍率下，5℃內阻估計誤差最大且不超過4mW；在0.562 5充電倍率下，25℃內阻估計誤差最大且不超過4mW；在0.937 5充電倍率下，25℃內阻估計誤差絕對值最大且不超過6mW。這表明在不同充電倍率和SOC的變化下內阻估計值與實驗值之間保持較好的一致性，驗證了所提出的多因素動態充電內阻模型能夠較好地估算不同溫度、不同SOC及不同充電倍率的充電內阻。

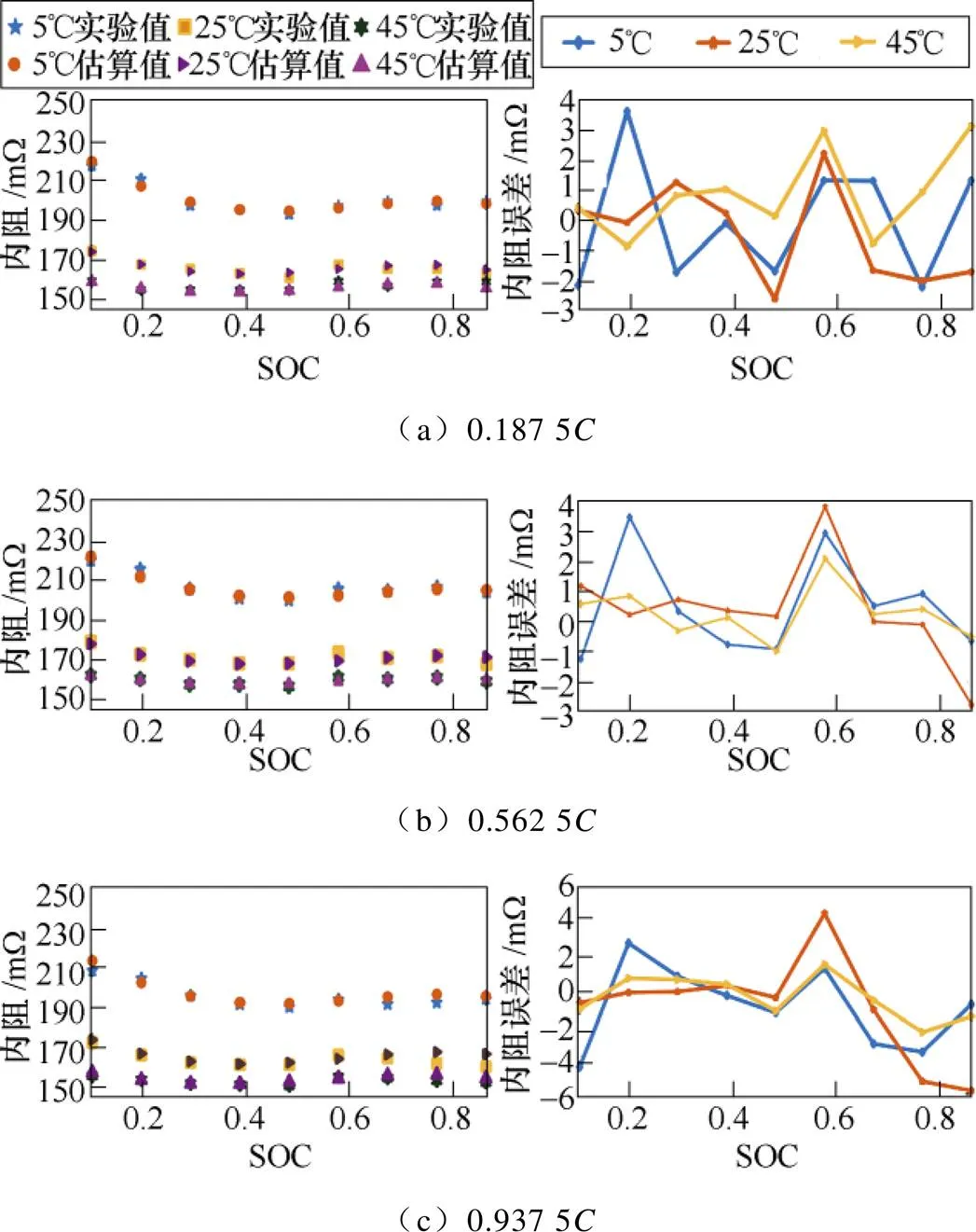
圖6 充電內阻估算結果

5 結論

1）通過分析鋰離子電池的實際充電數據，研究電池內阻受電池SOC、溫度和充電倍率的影響，并得到電池內阻和這些影響因素之間的關系。采用最小二乘法的二元多項式構建以充電內阻為因變量、溫度和SOC為自變量的二元四次多項式函數描述該關系。

2）提取不同充電倍率下的二元多項式函數系數組，采用三次樣條插值法擬合，構建出以溫度SOC和充電倍率為自變量，充電內阻為因變量的多因素動態內阻模型。實驗驗證結果表明，所建立的動態內阻模型在多種倍率和溫度下能夠實現準確估算電池充電內阻，估算誤差不超過6mW。

[1] 田華, 王偉光, 舒歌群, 等. 基于多尺度、電化學-熱耦合模型的鋰離子電池生熱特性分析[J]. 天津大學學報(自然科學與工程技術版), 2016, 49(7): 734-741.

Tian Hua, Wang Weiguang, Shu Gequn, et al. Analysis of heat generation in a Li-ion battery based on a multi-scale and electrochemical-thermal coupled model[J]. Journal of Tianjin University (Natural Science and Engineering Technology Edition), 2016, 49(7): 734-741.

[2] 孫丙香, 劉佳, 韓智強, 等. 不同區間衰退路徑下鋰離子電池的性能相關性及溫度適用性分析[J]. 電工技術學報, 2020, 35(9): 2063-2073.

Sun Bingxiang, Liu Jia, Han Zhiqiang, et al. Per- formance correlation and temperature applicability of Li-ion batteries under different range degradation paths[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2063-2073.

[3] 潘海鴻, 呂治強, 李君子, 等. 基于灰色擴展卡爾曼濾波的鋰離子電池荷電狀態估算[J]. 電工技術學報, 2017, 32(21): 198-205.

Pan Haihong, Lü Zhiqiang, Li Junzi, et al. Estimation of state of charge of lithium ion battery based on grey extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 198-205.

[4] 何錫添, 孫丙香, 阮海軍, 等. 鋰離子電池變頻變幅交流低溫自加熱策[J]. 電工技術學報, 2019, 34(9): 1798-1805.

Hen Xitian, Sun Bingxiang, Ruan Haijun, et al. A variable-frequency and variable-amplitude AC low- temperature self-heating strategy for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1798-1805.

[5] Gümü?su E, Ekici ?, K?ksal M. 3-D CFD modeling and experimental testing of thermal behavior of a Li-ion battery[J]. Applied Thermal Engineering, 2017, 120: 484-495.

[6] Nazari A, Farhad S. Heat generation in lithium-ion batteries with different nominal capacities and chemistries[J]. Applied Thermal Engineering, 2017, 125: 1501-1517.

[7] Waag W, Fleischer C, Sauer D U. Adaptive on-line prediction of the available power of lithium-ion batteries[J]. Journal of Power Sources, 2013, 242: 548-559.

[8] 陳英杰, 楊耕, 祖海鵬, 等. 基于恒流實驗的鋰離子電池開路電壓與內阻估計方法[J]. 電工技術學報, 2018, 33(17): 3976-3988.

Chen Yingjie, Yang Geng, Zu Haipeng, et al. An open circuit voltage and internal resistance estimation method of lithium-ion batteries with constant current tests[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3976-3988.

[9] 林春景, 李斌, 常國峰, 等. 不同溫度下磷酸鐵鋰電池內阻特性實驗研究[J]. 電源技術, 2015, 39(1): 22-25.

Lin Chunjing, Li Bin, Chang Guofeng, et al. Experi- mental study on internal resistance of LiFePO4batteries under different ambient temperatures[J]. Power Source Eechnology, 2015, 39(1): 22-25.

[10] Ratnakumar B V, Smart M C, Whitcanack L D, et al. The impedance characteristics of mars exploration rover Li-ion batteries[J]. Journal of Power Sources, 2006, 159(2): 1428-1439.

[11] Liu Xingtao, Chen Zonghai, Zhang Chenbin, et al. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation[J]. Applied Energy, 2014, 123: 263-272.

[12] Waag W, K?bitz S, Sauer D U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application[J]. Applied Energy, 2013, 102: 885-897.

[13] 姜久春, 時瑋, 張言茹, 等. 磷酸鐵鋰動力電池阻抗譜參數分析[J]. 北京理工大學學報, 2014, 34(5): 470-474.

Jiang Jiuchun, Shi Wei, Zhang Yanru, et al. Impe- dance spectra investigation and parameter analysis of traction LiFePO4battery[J]. Journal of Beijing Institute of Technology, 2014, 34(5): 470-474.

[14] 盧艷華. 車用三元鋰離子動力電池內阻特性分析[J]. 電源技術, 2017, 41(5): 702-704.

Lu Yanhua. Impedance characteristics of lithium ion power battery with NCM cathode for electric vehicles[J]. Power Source Technology, 2017, 41(5): 702-704.

[15] 韋海燕, 鐘騰云, 潘海鴻, 等. 基于改進HPPC鋰離子電池內阻測試方法研究[J]. 電源技術, 2019, 43(8): 1309-1311.

Wei Haiyan, Zhong Tengyun, Pan Haihong, et al. Study on measurement method of internal resistance of lithium-ion battery based on improved HPPC[J]. Power Source Eechnology, 2019, 43(8): 1309-1311.

[16] Ahmed S H, Kang X, Shrestha S O B, et al. Effects of temperature on internal resistances of lithium-ion batteries[J]. Energy Resources Technology, 2015, 137(3): 1901-1905.

[17] Zhao X, De Callafon R A. Modeling of battery dynamics and hysteresis for power delivery predi- ction and SOC estimation[J]. Applied Energy, 2016, 180: 823-833.

Establishing a Dynamic Model of Lithium-Ion Battery Charging Internal Resistance Based on Multiple Factors

11111,2

（1. School of Mechanical Engineering Guangxi University Nanning 530004 China 2. Guangxi Key Laboratory of Electrochemical Energy Materials Collaborative Innovation Center of Renewable Energy Materials Nanning 530004 China）

Modeling the internal resistance of lithium-ion batteries is of great significance for the thermal management of batteries. The internal resistance of charging is affected by many factors such as temperature and charging rate. Therefore, the relationship between the battery's internal resistance change characteristics and various influencing factors (charging rate, state of charge and temperature) is analyzed. The binary polynomial method based on the least square and the cubic spline interpolation algorithm are used to calculate the battery charging internal resistance at different charging rates, SOC, and temperature. The dynamic model of the internal resistance of multi-factor dynamic charge is established, and the charging internal resistance is estimated in different states. The results show that the maximum error between the internal resistance estimated value by the dynamic model and the experimental value does not exceed 6 mW, which proves that the proposed method for modeling battery charging internal resistance is effective.

Charging internal resistance, multiple factors, internal resistance model, least squares, binary polynomial, cubic spline

TM911

10.19595/j.cnki.1000-6753.tces.200320

國家自然科學基金（51667006）和廣西自然科學基金（2015GXNSFAA139287）資助項目。

2020-04-01

2020-04-29

潘海鴻 男，1966年生，教授，博士生導師，研究方向為動力電池系統信號采樣及電池管理。E-mail: hustphh@163.com

陳 琳 女，1973年生，教授，博士生導師，研究方向為信號檢測與處理和電池管理。E-mail: gxdxcl@163.com（通信作者）

（編輯 陳 誠）