基于卡爾曼濾波的在線量子態估計優化算法
叢 爽, 張 坤
(中國科學技術大學自動化系, 安徽 合肥 230027)
0 引 言
量子狀態估計(quantum state estimation, QSE)又稱為量子態層析,是一種基于量子系統的測量結果,并將QSE問題轉化為一個多目標最優化問題,通過優化算法的求解重構出量子狀態的方法[1-2]。QSE是量子信息的基礎,同時也是實現量子系統狀態反饋操控的重要組成部分[3]。一個n比特量子系統的狀態可以由一個d×d(d=2n)維的密度矩陣ρ描述,該密度矩陣同時滿足半正定和單位跡的厄米矩陣約束。QSE基于瞬時投影(強)測量,需要對待測的量子狀態制備大量的全同副本,并進行完備的(d2-1)次測量[4-5]。由Silberfarb 提出的連續弱測量提供了一種新的獲取量子測量信息的方式[6-7]。通過連續弱測量,可以間接地獲取量子態的部分信息,同時對被測系統動力學特性的影響很弱,因此能夠對量子系統實現在線的連續測量,為在線QSE提供了可能性[8]。由于QSE需要用到較多的測量數據,并通過多次迭代處理整個測量數據集來估計狀態,一般都是離線進行,而且多次測量和多次迭代所估計出的只是一個固定的量子態[9-10]。在離線QSE的算法方面,已經取得了很多研究成果,尤其在基于交替方向乘子法(alternating direction multiplier method, ADMM)的優化算法方面[2,4,11-13]。
在線QSE不僅要考慮每次只能在線獲取的一個測量值, 還要兼顧到系統的狀態是隨時間在線變化,也就是說, 在線量子態估計是對在線動態變化的量子態進行估計,這對在線QSE及其算法的實現提出了更大的挑戰[14]。在線QSE的算法方面,Silberfarb等人首先通過量子繪景變換,利用極大似然法,將動態的時變QSE轉化為對靜態初始狀態的估計[6-7]。Cong 等人提出了一種對時變量子態的在線估計算法,將每個采樣時刻的狀態估計問題轉化為一個約束最小二乘問題, 并利用Matlab凸優化工具箱進行求解[15-16]。極大似然法和凸優化工具箱本質上均為離線算法,其在線狀態估計過程實際上是一種雙層嵌套算法,即在每一時刻的在線優化過程中,執行多次的算法迭代,而不是每一次只執行一次算法迭代。Tsuda和Youssry等人提出利用矩陣指數梯度(matrix exponential gradient, MEG)的量子態在線學習算法[17-18]。Zhang等人提出一種基于在線鄰近梯度下降法(online proximal gradient descent method, OPG)和ADMM的量子態在線估計算法(簡稱為OPG -ADMM)[19-21]。本質上MEG和OPG -ADMM均是利用一階隨機梯度信息進行狀態在線更新。卡爾曼濾波(Kalman filter,KF)是一種時域狀態濾波算法,被廣泛應用于含有隨機擾動和測量噪聲的系統狀態估計或動態目標跟蹤系統中[22-24]。
本文將KF應用到在線QSE中,推導出滿足密度矩陣半正定和單位跡厄米矩陣約束的KF在線QSE優化算法。對于動態變化的量子狀態,在每一個采樣周期里,以在線測量一次估計一次的方式,進行一系列的在線量子態重構, 實時估計出動態變化的量子狀態。
由于待估計的狀態密度矩陣ρk的維度為d×d,對量子系統輸出值的每一次測量僅能獲得一個含有噪聲的測量輸出值。因此,本文首先通過演化算符的繪景等價變換,利用k時刻以及k以前所有時刻的測量值構造出測量值序列,作為對當前k時刻狀態估計的測量數據。然后,通過將帶有量子態約束條件的KF優化問題,分解成兩個凸優化子問題,先求解一個無約束條件下基于在線KF算法的量子測量更新問題的解析解,再考慮量子約束條件,通過求解矩陣的投影,在量子測量更新的基礎上獲得估計狀態的解析解。以此方式解決基于KF的在線QSE的應用問題,提出并實現一種實時重構動態量子狀態的在線KF算法,稱之為基于KF在線QSE(Kalman filter based online quantum state estimation, KF-OQSE)優化算法。將所提的KF-OQSE算法應用于估計4量子位系統的狀態密度矩陣,并與OPG -ADMM和MEG作性能對比分析。
本文基于連續弱測量的開放量子系統演化模型以及測量值序列的構造,推導了在線量子態KF算法,最后進行數值仿真實驗及其性能對比。
1 基于連續弱測量的隨機開放量子系統以及測量值序列的構造
一個n比特量子系統可以由薛定諤繪景下的連續隨機開放量子系統主方程[25]描述為
(1)

量子狀態在線估計的過程如圖1所示,由連續弱測量過程和量子狀態在線估計器兩部分組成。

圖1 基于連續弱測量的量子狀態在線估計過程Fig.1 Online quantum state estimation process based on continuous weak measurement
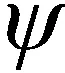


1.1 n-比特開放量子系統離散演化模型
n-比特量子系統的弱測量算符M(Δt)可以由m0(Δt)和m1(Δt)的張量積計算為
(2)

(3)
根據式(1)的隨機開放量子系統主方程以及式(3)的演化算符,通過令t=Δtk,被測量子系統S的動態離散演化模型為
(4)
式中,k=1,2,…,N表示采樣時間。
式(4)可以通過線性化變換為
(5)
式中,vec(X)表示將矩陣X的所有列組合串聯為一個列向量。
連續弱測量過程中作用在被測系統狀態上的測量算符的動態離散演化模型為
(6)
1.2 連續弱測量輸出序列的構造

(7)


實際應用中,測量值序列bk=[y1,y2,…,yk]。當然,對于從k=1采樣時刻起的QSE,由于測量總次數少于完備次數,所估計出的狀態一定是不準確的。隨著在線測量次數的增加,在達到一定測量次數后,就可以實現對隨時間變化的動態量子態的高精度估計。
采用本文所提出的測量數據值序列bk的構造方法,可以直接估計出每一個k時刻的量子狀態ρk。然后,再通過把初始狀態ρ1代入量子狀態演化模型,通過k步演化,得到k時刻的量子狀態。
測量采樣次數k是可以無限增大的,但不能一味地增加測量值序列的長度,增加計算負擔,并且在一定的測量次數下,就可以能獲得較高的估計精度。考慮到估計精度以及在線處理的計算代價,在量子態的在線估計中,本文限制并且固定一個測量值序列的長度,從第一次測量獲取數據開始,直到給定的測量長度,每一次新獲得的測量數據將替代掉已有數據序列中最早獲取的一個數值,從而始終保持估計數據序列限制在給定的長度里,稱為滑動窗口, 滑動窗口的更新策略為先進先出。由此可得實際QSE中所使用的帶有滑動窗口的測量值序列為
(9)
式中,l為測量值序列的滑動窗口長度。
根據式(8),構造與式(9)對應的采樣矩陣為

(8)
(10)
考慮到弱測量過程中不可避免地存在測量噪聲,結合式(9)和式(10),將測量值序列bk重寫為
bk=Akvec(ρk)+ek
(11)
式中,ek∈Rk(l 由此得到對連續弱測量過程中的量子系統離散狀態演化模型式(4),以及所構造的用于在線QSE的測量值序列式(11)。 本節將通過兩步來進行基于KF的在線QSE優化算法的設計及其求解過程的推導:① 量子預測狀態的時間更新,在此過程中,量子態濾波器基于上一時刻估計狀態和系統預測模型,對當前時刻狀態進行預測;② 量子估計狀態的測量修正和投影,在此過程中,量子態濾波器利用對當前狀態的觀測值對預測狀態值進行修正, 以獲得當前時刻狀態的估計值。 式(5)中的量子狀態的預測方程為 (12) (13) 式(13)可以轉化為一個凸優化問題: (14) 由于存在量子約束,對于式(14),直接求解帶有量子態約束條件的QSE測量更新的凸優化問題,以及推導滿足約束下的卡爾曼增益矩陣是十分困難的。為了能夠保證所估計出的量子狀態滿足量子約束條件,通過兩步運算來實現在線求解: 步驟 1當忽略狀態約束C時,優化問題式(14)退化為一個較容易求解的無約束二次凸優化問題: (15) (16) 基于求逆公式[27]: 可以求得式(16)為 同時, 通過定義卡爾曼增益矩陣為 (17) 則式(16)可以重寫為 (18) 需要強調的是,通過式(17)所獲得的卡爾曼增益矩陣Kk是無約束下的最小方差估計值。結合式(13)和式(18),可以推導出: (19) 式中,Q為系統隨機噪聲先驗統計特征。 (20) (21) (22) (23) 式(23)的拉格朗日函數為 (24) (25a) (25b) (25c) (25d) (26) (27) 本文所提KF-OQSE算法具體步驟如下所示。 算法 1 KF-OQSE算法初始化:變量^ρ0,W0,滑動窗口長度l∈Z+;步驟 1 for k=1,2,… do步驟 2 獲取測量輸出bk;步驟 3 根據式(13)計算時間更新預測狀態ρpre;步驟 4 根據式(17)計算增益矩陣Kk;步驟 5 根據式(18)和式(19)分別計算中間的測量更新 ρk以及矩陣Wk+1;步驟 6 對(ρk+ρ?k)/2進行特征值分解得到Udiag{ai}U?;步驟 7 根據式(26)和式(27)計算出{σ?i}di=1;步驟 8 根據式(22)獲得當前時刻最優估計狀態^ρ?k;步驟 9 end for 本節將通過數值實驗,將本文所提的KF-OQSE算法與其他已有的在線QSE算法對比,來驗證所提算法對動態量子態在線重建性能的優越性。實驗以n=4量子位系統為研究對象,系統相互作用強度ξ=0.7,外加控制量強度ux=2,系統測量效率η=0.5,系統隨機噪聲dW幅值為0.01;高斯測量噪聲信噪比(signal to noise ratio, SNR)為40 dB。 (28) (29) 保真度的值在0和1之間,越接近于1則認為兩個量子狀態越相似。在本文中, 所提KF-OQSE算法將分別與基于MEG[18]以及基于在線鄰近梯度ADMM(online proximal gradient-ADMM, OPG -ADMM)[21]的在線QSE算法作對比。正如在引言部分所提, 基于極大似然估計法[6-7]和凸優化工具箱[16]的在線估計算法,在每次狀態估計時內部都需要多次迭代,這個過程是相當耗時的,因此在本文中不作對比。OPG -ADMM算法首先通過引入輔助變量,并利用ADMM,將量子態在線估計問題分解為兩個分別關于量子態和測量噪聲的子問題,并通過在線臨近梯度法進行交替優化求解。MEG算法本質上仍然是利用一階梯度信息進行量子態更新,主要區別在于對量子態密度矩陣取對數和指數操作,通過矩陣的指數和跡歸一化操作保證估計狀態滿足量子約束。在數值實驗中, 對于KF-OQSE算法,初始化狀態預測誤差的協方差矩陣W0=10Id2×d2,OPG -ADMM 和MEG算法的參數均調至最優。數值仿真實驗運行環境為Matlab 2016 a,2.2 GHz Inter Core i7-8 750H CPU,內存16 GB。 圖2 不同滑動窗口長度下3種算法在線估計性能對比Fig.2 Performance comparison of three online estimation algorithms under different sliding window sizes 數值仿真實驗固定滑動窗口長度l=40,分別對比KF-OQSE,OPG -ADMM和MEG算法對4 量子位動態量子狀態的在線重構精度和估計耗時。圖3為3種算法在每一采樣時刻,在線估計狀態的歸一化估計誤差曲線圖。 圖3 固定滑動窗口長度下3種算法的在線估計性能對比Fig.3 Performance comparison of three online estimation algorithms under fixed sliding window size 圖4 k=100時真實以及估計的密度矩陣幅值和保真度Fig.4 Density matrix amplitude and fidelity of the real state and the estimated state with k=100 所提算法在處理多比特量子系統時,對于在線獲取的測量值,首先采用滑動窗口構造測量值序列,滑動窗口的設計可以認為是在線計算量和估計效能的折中,更加適合于在線的應用場景。KF-OQSE算法能夠在每次的狀態估計中,僅通過一次迭代就得到當前采樣時刻的估計值。同時,KF本身就是一種在線估計,可以有效地對動態目標進行實時跟蹤,因此本文所提算法可以進行實時連續在線估計。 對于連續弱測量中的動態量子系統狀態,本文提出了一種帶有量子約束條件的KF的量子態在線估計算法KF-OQSE。所提算法采取量子預測狀態的時間更新-量子估計狀態的測量修正和投影的更新策略,求解具有量子態約束的卡爾曼優化問題。此外,為了獲得較高的估計效率,采用了測量輸出序列的滑動窗口。數值實驗結果表明,所提算法能夠以更少的采樣次數和耗時實現高精度的量子態在線估計,驗證了KF-OQSE算法作為多量子位系統狀態在線估計方案的優越性。2 基于KF算法的在線QSE優化算法
2.1 量子預測狀態的時間更新


2.2 QSE的測量修正和投影














3 在線QSE數值實驗及其結果分析



3.1 不同滑動窗口長度下算法在線估計效能對比



3.2 固定滑動窗口長度下算法在線處理性能對比





4 結 論

