大數據技術在輸變電工程造價指標預測中的應用研究

劉哲, 何子東, 靳健欣, 張德廣, 董楦

(1.國網河北省電力有限公司， 河北 石家莊 050022; 2.國網河北省電力有限公司 經濟技術研究院， 河北 石家莊 050022;3.河北省送變電有限公司， 河北 石家莊 050070)

0 引言

科技的進步推動著各行各業不斷地進行著發展，電力建設的規模也隨之而持續擴大，輸變電工程的投資與造價不斷攀升[1]。基于此，電力網絡企業承擔著超負荷的市場壓力，輸變電工程造價由于受到多方面多角度的影響，包括社會環境、自然環境與經濟發展等眾多因素的影響，產生了越來越高的管理要求[2]。為了改變這一現狀，亟需構建一種合理高效的輸變電工程造價指標預測模型[3]。當今社會中，許多輸變電工程造價的模型均存在弊端，不能為工程建設的順利實施提供有力的幫助[4]。有鑒于此，此次研究將針對大數據技術，以及輸變電工程造價的影響因素等進行深入的分析，旨在為未來的輸變電工程造價指標預測提供參考。

1 輸變電工程造價指標預測方法

1.1 輸變電工程造價影響因素分析

對輸變電工程的相關影響因素進行分析，指的是對輸變電工程的基礎項目數據進行收集整理，對該數據之間的相互關系進行分析，最終獲得影響因素及其影響力[5]。針對輸變電工程造價影響因素進行分析，詳盡的技術路線圖如圖1所示。

在對影響因素進行識別的過程中，須對整個過程的環節進行合理的劃分，從自然因素與技術條件兩個方面著手，來構建工程造價影響因素庫。輸變電工程造價項目主要包含六個部分，分別為可行性研究階段、設計方案選擇和初步設計階段、技術設計和施工圖設計階段、招投標階段、施工階段，以及竣工階段。在可行性研究階段，主要影響因素包括政治、經濟與自然三方面的風險，以及工程復雜度等等，具體內容如圖2所示。

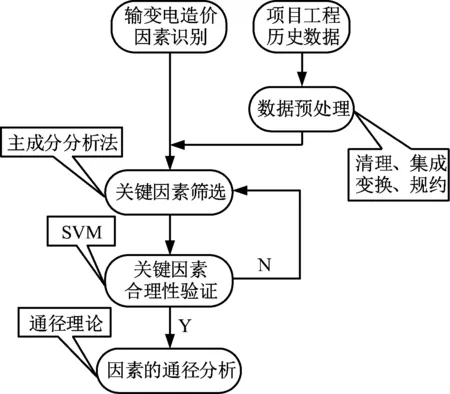
圖1 輸變電工程造價影響因素分析的技術路線

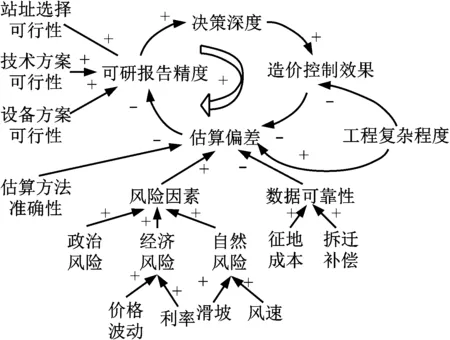
圖2 系統動力學流圖之可行性研究階段

由圖2可知，可行性研究階段的主要工作為可行性研究報告的擬定，該報告需要具有一定的真實性與科學性。其中顯示出可行性研究報告的站址選擇、技術方案與設備方案決定著該報告的精度，與輸變電工程決策的精度與深度緊密相關。對投資方案進行擬訂，隨后再按照投資目標進行比較，選擇出最優投資方案。除此以外，在設計及招投標階段部分，其系統動力學流圖如圖3所示。

圖3 系統動力學流圖之設計、招投標階段

由圖3可知，設計階段作為輸變電工程建設的核心，其規劃、數據、圖紙與技術等均為實現項目工程的建設起到重要的指導作用。工程造價的主要任務目標是對項目中的技術先進性與經濟合理性進行協調化處理，盡可能地降低估算與概預算之間存在的偏差。還需結合設備數量、規劃難度與技術要求，提高預算方法的準確性。隨后進入施工與竣工階段，對建設資源的實際值與目標值之間的偏差進行動態分析及管控[6]。

1.2 基于輸變電工程造價指標預測的模型構建與造價估算

為了對輸變電工程造價中的各項指標信息進行準確地預測，此次研究采用支持向量機(Support Vector Machine，SVM)來構建模型，支持向量機是一種機器學習方法，其監督學習流程如圖4所示。

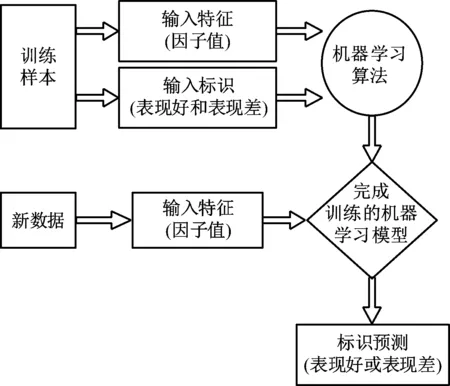
圖4 SVM監督學習流程示意圖

SVM對訓練樣本進行監督學習，對輸入特征進行分類，再將提前選擇的非線性映射用來對訓練樣本進行處理，將訓練樣本映射到高維特征空間后，創建最優分類超平面，最終獲取到復雜度較小的特征函數集。此最優超平面如圖5所示。

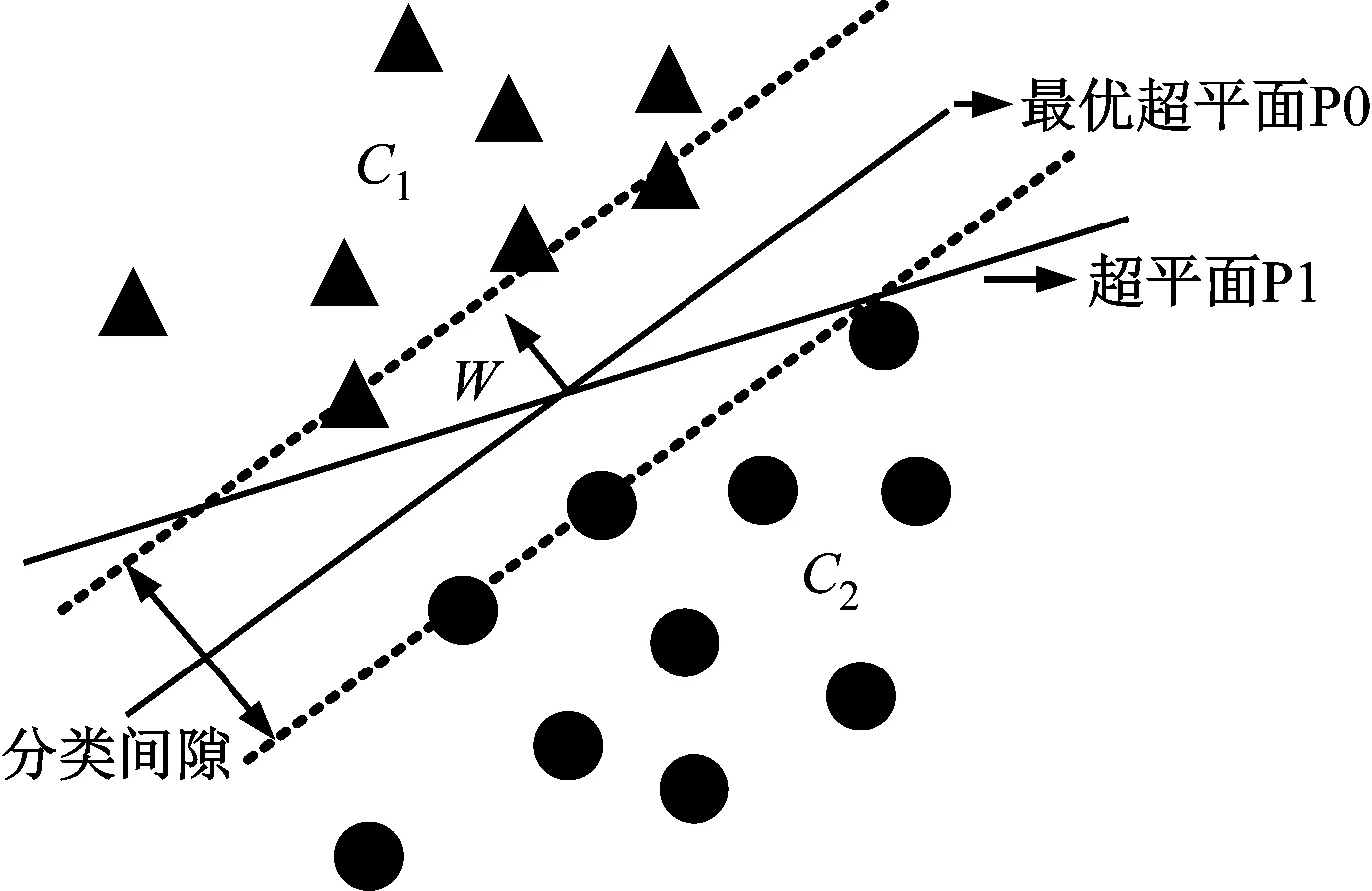
圖5 最優超平面示意圖

圖5中的C1與C2分別代表著二維數據樣本；P0與P1則指的是不同的分類函數。前者即最優超平面分類函數，后者為普通超平面分類函數。SVM模型的泛化性較強，能夠快捷高效地處理高維數據，因此其被廣泛應用到小樣本、非線性和高維等數據的分析處理中。此次研究中為了提高模型的精度，應用更具優越性的最小二乘支持向量機(Least Squares Support Veotor Maohine，LS-SVM)，將SVM的訓練過程靈活轉換為線性方程組的求解過程。LS-SVM令訓練樣本集為Sl，表明該樣本集的大小為l。在此條件下，則有Sl={(xi,yi),i=1,2,…,l}，且xi,yi∈Rn。LS-SVM通過機器學習，依據樣本集的變化規律來獲取相應的數據預測值，則有式(1)。

f(x)=wTφ(x)+b

(1)

式中，w∈Rn指的是該模型中的權向量；b指的是偏置項；φ(x)是低維空間到高維特征空間的映射函數。將該線性關系進行一定的轉換，如式(2)。

(2)

式中，αk代表著誤差變量；k=1,2,…,l；γ表示的是可調系數。隨后再運用拉格朗日函數對獲取到的線性關系進行轉換，得到式(3)。

式中，λk表示的是拉格朗日乘子，隨后再求偏導數，式(4)。

(4)

在該模型中存在核函數，令核函數為K(xk,xh)，則有式(5)。

K(xk,xh)=φ(xk)Tφ(xh)

(5)

核函數被選擇確定為徑向基(Radial Basis Function，RBF)核函數，如式(6)。

(6)

式中，核函數的寬度系數表示為g，因此可以得到該模型中樣本的預測值為yk，如式(7)。

(7)

根據式(1)至式(7)，再結合輸變電工程中的歷史數據，可以得到訓練樣本集{(xi,yi),i=1,2,…,l}，輸入向量表示為xi；輸出向量的期望值表示為yi；樣本個數仍然以l來表示。隨后再進行數據的歸一化處理，以提高模型的訓練速度和精度。輸變電工程造價中的核心點在于投資問題，其中包括靜態投資與動態投資，在此過程中獲取到的數據均為小樣本數據，故而需要采用主成分分析法(Principal Component Analysis，PCA)，將對該工程造價中的相關數據信息進行處理，以獲取原始輸入集與輸出集，輸入集包含了輸入電壓等等，輸出集則表示為靜態投資，其特征值與相對應的貢獻率如圖6所示。

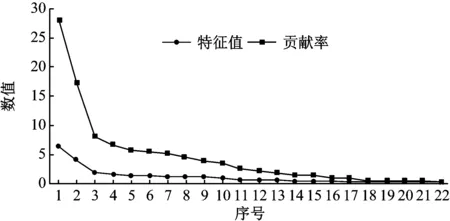
圖6 特征值和主成分貢獻率分析

圖6中的特征值為k，貢獻率以百分比來表示。其中輸入集共含有22個指標，輸出集指的是靜態投資，僅有1個指標。第一主成分擁有的原始指標信息量最多，往后依次減少。所有主成分相對應的特征值均為正數，主成分包含初始指標的數據量與主成分的值呈負向相關關系。

2 實驗與分析

通過構建輸變電工程造價指標預測模型的方式，采用SVM與LS-SVM對樣本進行估算。首先將樣本集輸入到SVM網絡中進行學習，并多次重復學習過程；隨后利用測試樣本得到最優的參數值，再將目標樣本輸入其中進行估算，最終將得出的結果與真實值進行對比分析，輸電工程造價估算模型的實驗結果如圖7所示。

圖7 不同估算結果與實際值對比

根據圖7可知，當測試樣本數量為1時，原始靜態的估算值為485萬元，SVM與LS-SVM的估算值分別為435萬元與500萬元；當測試樣本數量為3時，原始靜態的估算值為405萬元，SVM的估算值為465萬元，而LS-SVM為450萬元。綜上所述，當測試樣本的數量不同時，SVM與LS-SVM的估算值也會隨之而產生變化，然而無論處于何種樣本數量值時，LS-SVM的估算值均更加靠攏實際值，這表明LS-SVM的預測精度更高，預測的準確性更強。在LS-SVM模型中，為了更加精確地分析清楚模型的預測準確度，還采用了不同的核函數來進行橫向對比，結果如表1所示。

表1 輸電工程中不同核函數輸出的結果對比分析

表1中展示了在LS-SVM估算模型中，基于RBF核函數與Lin核函數輸出的不同結果。通過將實際值、RBF核函數與Lin核函數三種輸出結果進行對比可知，若選用傳統的Lin核函數，該模型的絕對誤差最小值為7.69萬元，絕對誤差的最大值為86.78萬元；當選用RBF核函數時，絕對誤差的最小值僅為2.58萬元，相對應的絕對誤差最大值則為14.84萬元。不同核函數的輸出結果對比圖如圖8所示。

圖8 估算結果與實際值對比

通過圖8 不同數量的測試樣本的估算結果來看，選用RBF核函數的估算精度更高，其估算值更加接近于原始靜態值。當測試樣本個數為3時，原始靜態值為410萬元，Lin核函數的估算值為500萬元，二者間的誤差高達90萬元；與此同時，RBF核函數的估算值則為402萬元，與實際的原始靜態值之間僅存在8萬元的誤差。因此，RBF核函數的估算準確度顯著高于Lin核函數。

3 總結

我國電力水平不斷提高，推動電力工程與社會經濟同步持續增長勢在必行。為了做好輸變電工程造價的管控，此次研究對輸變電工程造價中的各項影響因素進行了細致的探究，利用大數據相關技術構建了優化后的支持向量機模型，提出了一種新的工程造價管理方法。結果顯示，在輸變電工程的LS-SVM估算模型中，運用RBF核函數來對工程造價進行估算是最優選擇，其估算準確性更強，預測精度更高。此次研究有幸取得了一定的研究成果，然而由于個人能力的限制，在研究中仍然存在一些亟待完善的地方，如進行變電工程中不同核函數估算的工程數量較少。在未來的研究中，希望能進行更加全面客觀的探究。