表面有螺旋裝飾條的大跨貝殼形屋蓋風荷載特性

林擁軍 ，林池錟 ，周 祎 ，劉開齊 ，潘 毅

（1. 西南交通大學土木工程學院，四川 成都 610031；2. 南充市審計局，四川 南充 637003）

大跨屋蓋結構具有柔性大、阻尼小、自振頻率低等特點，對風荷載十分敏感[1-3]. 其中，大跨貝殼形屋蓋結構因造型獨特、體型復雜，風荷載在屋面的流動分離作用十分復雜. 但是，已有文獻和現行規范[4]并沒有類似外形的體型系數可供參考. 同時，為彰顯建筑物的藝術表現力，屋蓋表面往往需要設置肋條、波紋等復雜的建筑裝飾構件[5]. 在裝飾構件尺寸日趨大型化、布置形式復雜多變的情況下，屋蓋特征湍流以及風荷載的作用機理與普通大跨貝殼形屋蓋有很大的不同[6].

目前，在建筑物表面裝飾構件對結構風荷載特性的影響研究方面，Montazeri等[7]采用計算流體動力學 （computational fluid dynamics，CFD）方法研究了外挑陽臺對高層建筑風壓分布的影響，結果表明陽臺的細部構造對建筑立面的風荷載分布影響很大；Yuan等[8]通過風洞試驗模型的研究，發現高層建筑表面附屬構件會減小迎風面局部最大正壓峰值和側面局部負壓峰值；艾輝林等[9]采用CFD數值模擬技術研究了超高層建筑外表面裝飾條的風荷分布規律及其風載控制系數；全涌等[10]進行了建筑局部外形對圍護結構風荷載特性影響的試驗研究，結果表明最大正風壓系數并不受局部外形的影響，但對最大負風壓系數的影響較大；沈國輝等[11]研究了設有外鏤空裝飾的扭轉體型高層建筑的風荷載，結果表明裝飾結構能明顯減小主體結構側風面風壓的平均值和脈動效應.

綜上所述，已有關于裝飾構件對結構風荷載特性影響的研究主要集中于高層建筑和懸挑結構，針對大跨屋蓋，特別是大跨貝殼形屋蓋的研究還鮮有報道. 由于大跨貝殼形屋蓋與高層建筑以及懸挑結構的結構特性具有很大的不同，主體結構和局部構件的風荷載分布規律也不一樣. 因此，亟需對外表面有復雜裝飾條的大跨貝殼形屋蓋的風荷載特性進行研究，了解表面裝飾造型對屋面風壓分布的影響，為類似結構的抗風設計提供參考.

在已有關于結構風荷載特性的研究方法中，風洞試驗雖然已廣泛應用于工程結構的抗風性能評估，但要考慮裝飾構件對大跨度結構的影響卻非常困難，主要原因在于裝飾構件的尺寸相對較小，一般的縮尺模型難以呈現其幾何特征，而采用較大的縮尺模型除成本較高之外，一般風洞還難以滿足阻塞比的要求. 與風洞試驗相比，CFD方法具有可以建立建筑原型尺度、周期短、成本低等優點，已廣泛應用于大跨翹曲屋蓋、復雜體型高鐵站房屋蓋、可伸縮大跨體育場館屋蓋等大跨結構的風荷載特性研究[12-15].

為此，本文以某大跨高鐵站房屋蓋為對象，采用CFD方法，基于高性能計算機工作站和Rhino、Fluent15.0 軟件平臺，建立了該大跨貝殼形屋蓋的數值風洞模型，并采用風洞試驗數據對其可靠性和適用性進行驗證. 除建立有表面裝飾條 （surface decorative strips，SDS）的數值風洞模型之外，還建立了無表面裝飾條 （no surface decorative strips，NSDS）的數值風洞模型，研究了表面裝飾肋條對屋蓋風荷載特性的影響，并分析了其受力機理.

1 計算流體力學理論

湍流模擬采用工程中常用的雷諾平均法（RANS），并將大氣邊界層內建筑物周圍低速流動的空氣視為不可壓縮流體，其基本控制動量方程（Navier-Stokes方程）和連續方程[16]分別如式（1）、（2）.

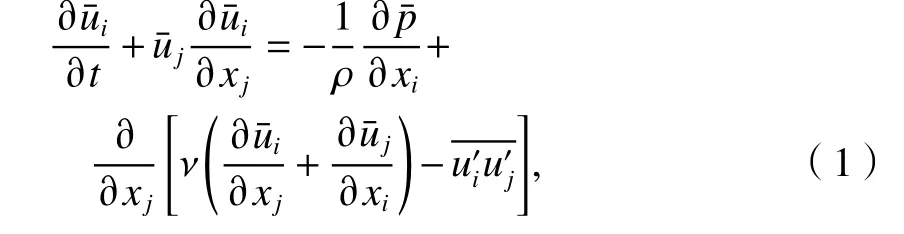
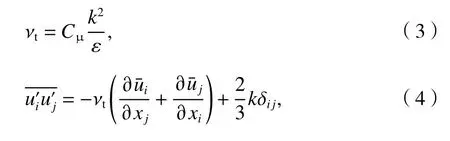
式中：δij為克羅內克（Kronecker）函數；Cμ為經驗系數；k和ε如式（5）、（6）.

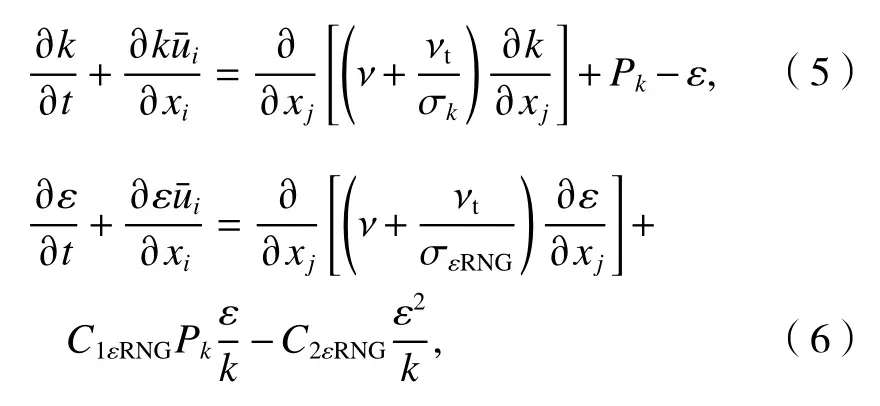
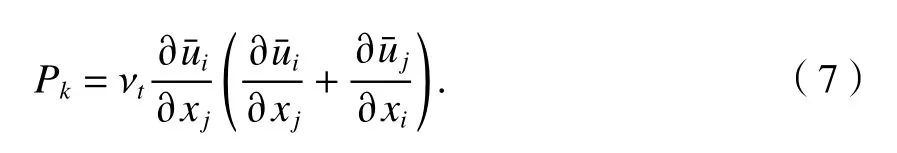
2 數值模型的建立

該屋蓋長跨143 m，短跨80 m，矢高24 m，其主體結構采用順時針和逆時針各36根雙螺旋鋼箱梁呈空間相交接而成四邊形網格，網格內填充有四周向中心有一定拱度的ETFE （ethylene tetra fluoro ethylene）氣枕，在屋蓋表面設有沿順時針鋼箱梁高出屋面約 50 cm的裝飾條，該屋蓋整體造型新穎獨特，類似于貝殼形，如圖1所示[17].

2.1 幾何建模及網格劃分

由于貝殼形屋蓋幾何形狀較為復雜，幾何模型的建立采用Rhino軟件進行. 屋蓋的幾何模型有兩種，分別為有表面裝飾條模型和無表面裝飾條模型. 有表面裝飾條模型與實際結構完全一致，裝飾條沿鋼箱梁螺旋布置，為200 mm × 500 mm的矩形截面，相鄰裝飾條間最大垂直間距（屋蓋底部）為3.965 m，最小間距（屋蓋頂部）為0.950 m，除建立了屋蓋結構表面的形狀之外，還呈現了ETFE氣枕（如圖2（a）所示）. 無表面裝飾條屋蓋模型僅考慮屋蓋結構表面的形狀，主要用作對比分析（如圖2（b）所示）.

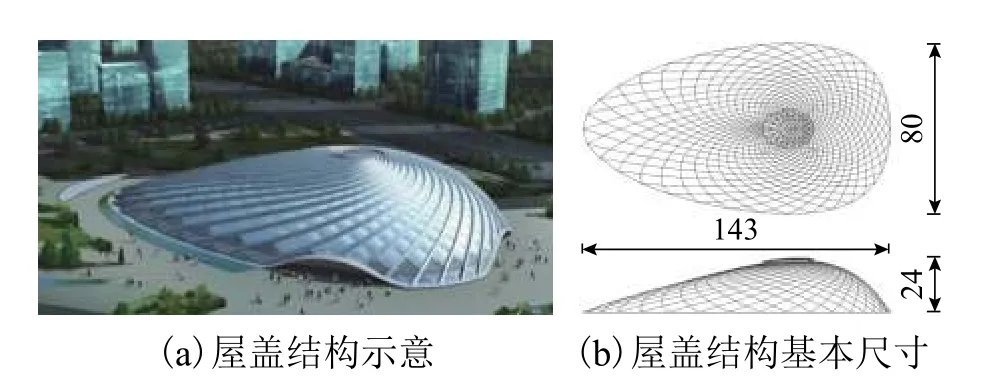
圖1 有表面裝飾條大跨貝殼形屋蓋（單位：m）Fig. 1 Large-span scalloped roof surface with decorative strips (unit：m)

圖2 貝殼形屋蓋幾何模型Fig. 2 Geometric model of shell-shaped roof

數值風洞模型流體計算域的確定也較為重要，Franke等[18-19]的研究表明：計算域的大小取決于建筑物覆蓋區域和邊界條件，根據該建筑物的實際尺寸（143 m（長） × 80 m（寬） × 24 m（高）），結合計算條件，將計算域取為1 200 m（長） × 800 m（寬） × 300 m（高）. 建筑物中心（結構平面長短軸交點）位于流場沿流動方向1/3處，中心距入口邊界5B，距出口邊界10B，距側面邊界5B，距頂面邊界10H，B和H分別為建筑物的寬度和高度，如圖3所示. 該數值風洞的阻塞率為0.57%，小于風洞試驗建議的3.00%，可以滿足模擬建筑物所處大氣環境的要求[20].

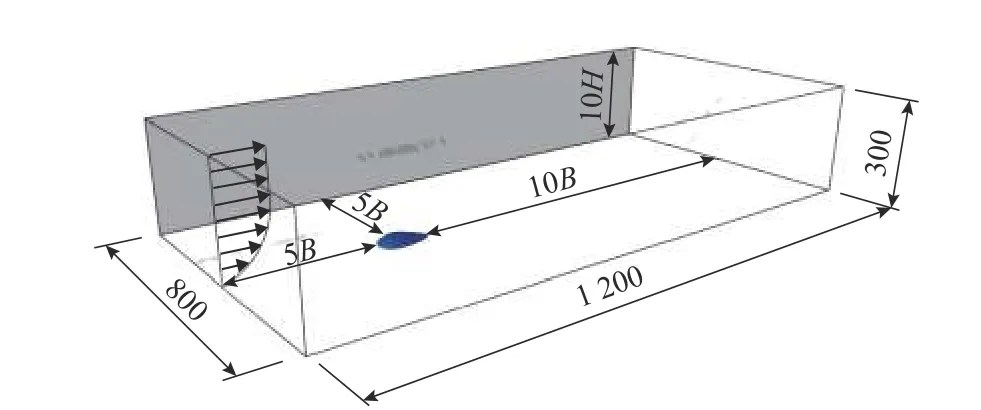
圖3 數值風洞的流體計算域和邊界條件（單位：m）Fig. 3 Fluid calculation domain and boundary conditions of numerical wind tunnel (unit: m)

在進行網格劃分時，采用了外流域使用結構化網格，建筑物表面使用非結構化網格的混合離散方法，網格尺寸隨距建筑物邊界距離的增大而增大. 相對于無表面裝飾條屋蓋，有表面裝飾條屋蓋由于表面裝飾條的存在，更加注重網格的精細化要求，對裝飾條及ETFE氣枕進行局部精細化加密. 運用處理軟件ICEM CFD 進行網格劃分，有表面裝飾條屋蓋共劃分網格單元3428941個，裝飾條旁最小體網格體積為1.178 × 105mm3，遠處最大體網格尺寸為6.034 × 107mm3. 無裝飾條屋蓋共劃分網格單元 2657728個，屋面局部網格劃分情況如圖4所示.

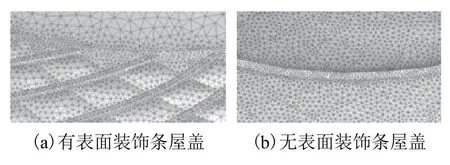
圖4 屋蓋表面局部網格劃分情況Fig. 4 Local meshing of the roof surface

2.2 邊界條件與求解

數值風洞的邊界條件如圖3所示. 入口邊界條件采用速度入口（velocity-inlet）模擬D類大氣邊界層風剖面，平均風速剖面、k和ε在入流口的分布均采用UDF編程與Fluent作接口實現. 出口邊界條件采用完全發展出流邊界條件（outflow），即流場任意物理量沿出口法向梯度為0. 計算域頂部和兩側采用對稱邊界條件（symmetry）來等價黏性流動中的無滑移壁面. 建筑物表面和地面采用無滑移的壁面條件Wall. 為計算方便，入口處湍流參數采用k和ε組合在邊界上賦值，如式（8）、（9）[20].

式中：V（Z）為平均風速，V（Z） =V10（Z/10）α，V10為模型前方來流未擾動區離地面10 m高度處的平均風速，α為地面粗糙度指數，取值 0.3；Z為離地高度；I為湍流強度；l為湍流積分尺度.

結合風洞實測數據，高度Z處的I和l計算如式（10）、（11）.

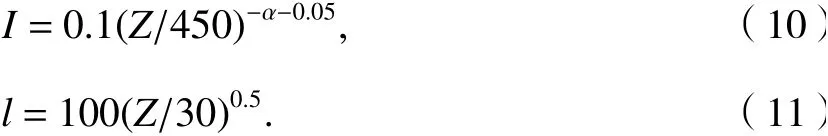
為保證計算的穩定性，對流項的離散選用了具有三階精度的二次迎風插值格式，速度壓力耦合采用SIMPLEC算法，同時各變量收斂殘差控制到10?5以下，以保證求解的精度.

3 數值模型的試驗驗證及分析

3.1 風洞試驗概況

試驗在西南交通大學風工程試驗研究中心XNJD-3大氣邊界層風洞中完成，風洞試驗段尺寸為36.0 m（長） × 22.5 m（寬） × 4.5 m（高）. 為考慮屋面裝飾條，模型縮尺比例取為1∶75，采用尖塔和立方體粗糙元組合的方法模擬D類風場，模型如圖5（a）. 風場風速比與湍流度剖面如圖5（b）所示（圖中：ZG、U、UG分別為參考點高度、風速和參考點處風速；Iu為湍流強度）.

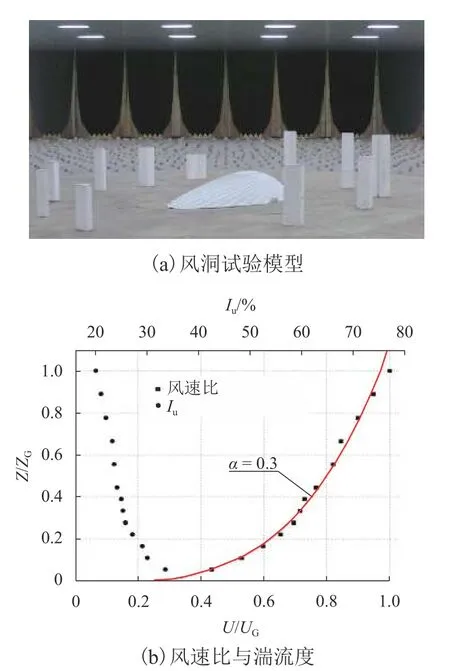
圖5 模型在風洞中的情況Fig. 5 Model in the wind tunnel

屋蓋結構表面共計布置673個測點，試驗風速為7 m/s，每個測點采樣時間為150 s，采樣頻率為200 Hz. 試驗風向角間隔為15°，共計測量了24個風向角，如圖6所示. 圖中：a1～a18、b1～b12均為測點. 每風向重復測量2次，所有壓力測點的脈動壓力時程同步獲得. 試驗結果表明，風荷載作用下，屋蓋以升力為主，屋蓋頂部區域風壓系數較大，各風向角下屋蓋頂部周邊區域的局部體型系數較其他區域大，屋蓋陡端區域局部體型系數較緩端局部體型系數大[16].

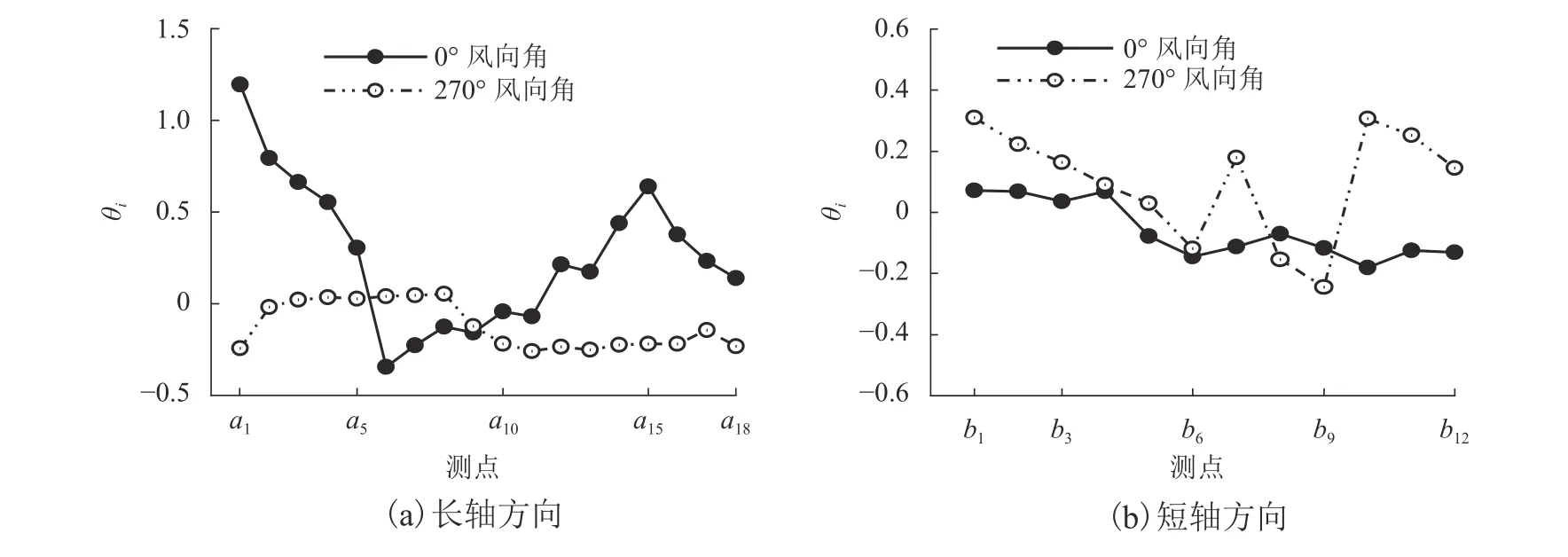
圖8 風壓系數偏差比隨測點的變化曲線Fig. 8 Variation curve of deviation ratio of wind pressure coefficient with measuring points

從圖7、8中可以看出：試驗值與計算值變化趨勢基本一致，總體而言，短軸方向平均風壓系數試驗值與計算值的差異較長軸方向小，270° 風向角較 0°風向角的差異小. 長軸方向：0° 風向角時，處于尾流區的遠端測點a1～a4的平均風壓系數試驗值與計算值的差異較大，風壓系數偏差比大于0.5，尾流區尾端測點a1的風壓系數偏差比約為1.2，其余測點風壓系數偏差比在 ± 0.5以內，說明數值模型對于尾流區的模擬仍有待于進一步研究；270° 風向角時，偏差比在 ± 0.26以內，長軸方向屋面緩端測點a10～a18的計算值比試驗值要高一些，主要原因可能在于測點附近裝飾肋條的旋轉方向為阻風向，氣流在局部的流向及流速會產生突變，在屋蓋上形成具有較高吸力特性的渦流，使得風壓系數計算值的絕對值大于風洞試驗. 短軸方向：0° 風向角時，偏差比在 ±0.18以內；270° 風向角時，偏差比在 ± 0.31以內.

3.2.2 屋面風荷載體型系數

為了解風荷載體型系數計算值與試驗值之間偏差情況，定義風荷載體型系數相對誤差為

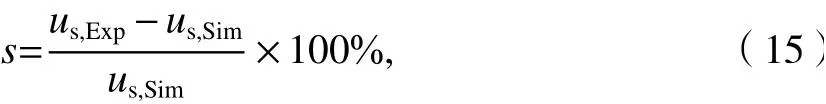
式中：us,Exp為風荷載體型系數試驗值；us,Sim為風荷載體型系數計算值.

將整個屋蓋分為27個區域， 0° 及270° 風向角下，經數值模擬和風洞試驗所得到的屋蓋局部區塊風荷載體型系數分布情況如圖9所示，圖中無框數字為數值計算結果，方框內數字為風洞試驗結果. 從圖中可以看出：0° 風向角時，來流側屋蓋前段的4個區塊的風荷載體型系數為正值，其余區塊的風荷載體型系數均為負值；270° 風向角時，除來流側的近端區塊風荷載體型系數為正值外，其余區塊的風荷載體型系數均為負值. 屋蓋各區塊風荷載體型系數計算值與試驗值的分布規律基本一致，風荷載體型系數大都為負值，以吸力為主，說明貝殼形屋蓋與圓球屋蓋及橢球屋蓋等大跨度結構具有相似風壓分布風特性[21-22]；0° 風向角時，除尾流區外，風荷載體型系數計算值略大于試驗值，屋蓋頂部區塊的風荷載體型系數最大，風荷載體型系數試驗值為 ?0.51，計算值為?0.54；270° 風向角時，在屋蓋的緩端及迎風面，風荷載體型系數計算值略大于試驗值，風荷載體型系數最大值出現在屋蓋頂部周邊區塊，風荷載體型系數試驗值為?0.69，計算值為?0.71.

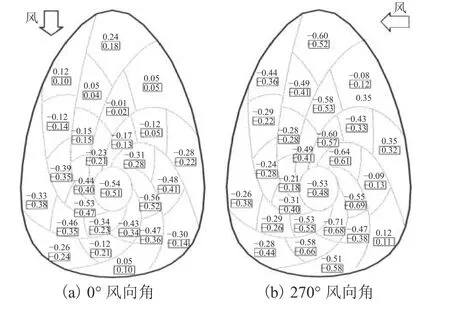
圖9 屋蓋局部區塊風荷載體型系數分布Fig. 9 Distribution of wind load shape coefficient of local block in the roof

在0° 及270° 風向角下，屋蓋各區塊風荷載體型系數相對誤差如圖10所示. 0° 風向角下，除屋面正負壓過渡區域風壓本身較小不具有參考價值，尾流區的數值模擬存在局限性[23]，相對誤差較大之外，其余區塊的風荷載體型系數相對誤差在 ± 25%以內. 與0° 風向角類似，270° 風向角下，除屋面正負壓過渡區域及尾流區的相對誤差較大之外，其余區塊的風荷載體型系數相對誤差也在 ± 25%以內.

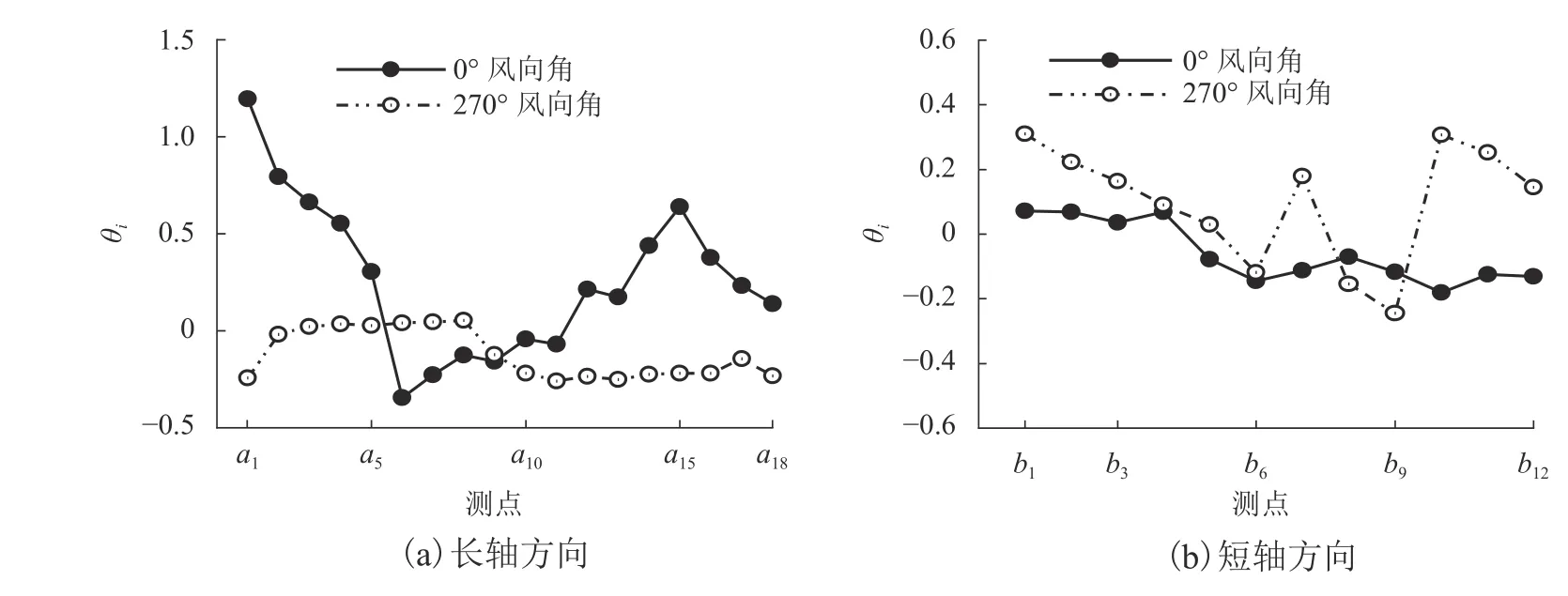
圖8 風壓系數偏差比隨測點的變化曲線Fig. 8 Variation curve of deviation ratio of wind pressure coefficient with measuring points

從圖7、8中可以看出：試驗值與計算值變化趨勢基本一致，總體而言，短軸方向平均風壓系數試驗值與計算值的差異較長軸方向小，270° 風向角較 0°風向角的差異小. 長軸方向：0° 風向角時，處于尾流區的遠端測點a1～a4的平均風壓系數試驗值與計算值的差異較大，風壓系數偏差比大于0.5，尾流區尾端測點a1的風壓系數偏差比約為1.2，其余測點風壓系數偏差比在 ± 0.5以內，說明數值模型對于尾流區的模擬仍有待于進一步研究；270° 風向角時，偏差比在 ± 0.26以內，長軸方向屋面緩端測點a10～a18的計算值比試驗值要高一些，主要原因可能在于測點附近裝飾肋條的旋轉方向為阻風向，氣流在局部的流向及流速會產生突變，在屋蓋上形成具有較高吸力特性的渦流，使得風壓系數計算值的絕對值大于風洞試驗. 短軸方向：0° 風向角時，偏差比在 ±0.18以內；270° 風向角時，偏差比在 ± 0.31以內.

3.2.2 屋面風荷載體型系數

為了解風荷載體型系數計算值與試驗值之間偏差情況，定義風荷載體型系數相對誤差為

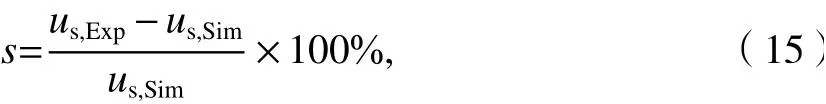
式中：us,Exp為風荷載體型系數試驗值；us,Sim為風荷載體型系數計算值.

將整個屋蓋分為27個區域， 0° 及270° 風向角下，經數值模擬和風洞試驗所得到的屋蓋局部區塊風荷載體型系數分布情況如圖9所示，圖中無框數字為數值計算結果，方框內數字為風洞試驗結果. 從圖中可以看出：0° 風向角時，來流側屋蓋前段的4個區塊的風荷載體型系數為正值，其余區塊的風荷載體型系數均為負值；270° 風向角時，除來流側的近端區塊風荷載體型系數為正值外，其余區塊的風荷載體型系數均為負值. 屋蓋各區塊風荷載體型系數計算值與試驗值的分布規律基本一致，風荷載體型系數大都為負值，以吸力為主，說明貝殼形屋蓋與圓球屋蓋及橢球屋蓋等大跨度結構具有相似風壓分布風特性[21-22]；0° 風向角時，除尾流區外，風荷載體型系數計算值略大于試驗值，屋蓋頂部區塊的風荷載體型系數最大，風荷載體型系數試驗值為 ?0.51，計算值為?0.54；270° 風向角時，在屋蓋的緩端及迎風面，風荷載體型系數計算值略大于試驗值，風荷載體型系數最大值出現在屋蓋頂部周邊區塊，風荷載體型系數試驗值為?0.69，計算值為?0.71.

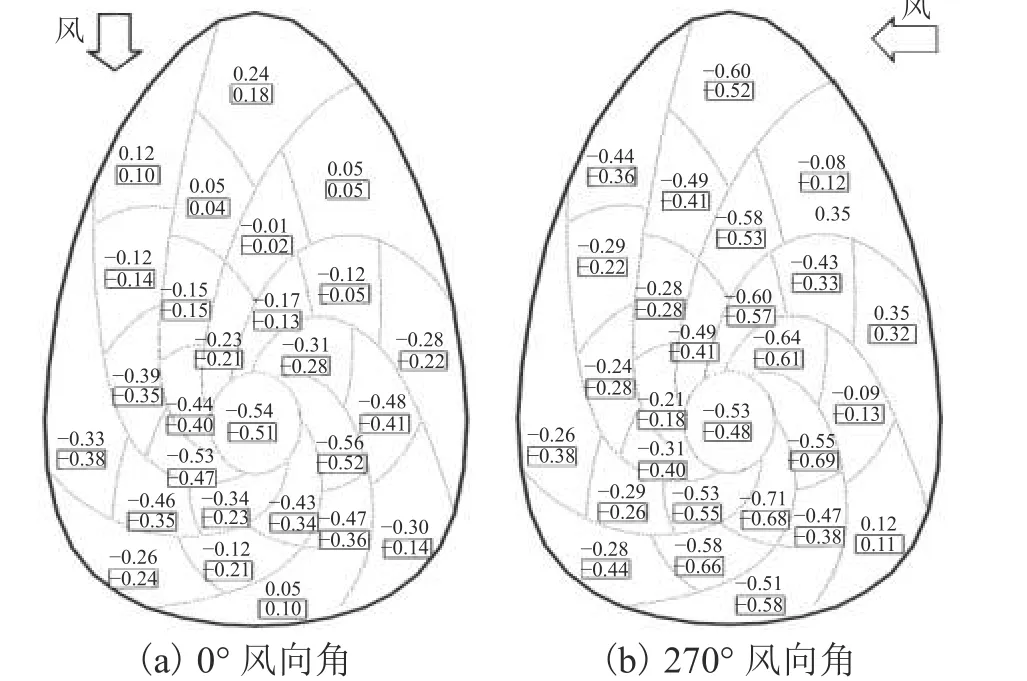
圖9 屋蓋局部區塊風荷載體型系數分布Fig. 9 Distribution of wind load shape coefficient of local block in the roof

在0° 及270° 風向角下，屋蓋各區塊風荷載體型系數相對誤差如圖10所示. 0° 風向角下，除屋面正負壓過渡區域風壓本身較小不具有參考價值，尾流區的數值模擬存在局限性[23]，相對誤差較大之外，其余區塊的風荷載體型系數相對誤差在 ± 25%以內. 與0° 風向角類似，270° 風向角下，除屋面正負壓過渡區域及尾流區的相對誤差較大之外，其余區塊的風荷載體型系數相對誤差也在 ± 25%以內.

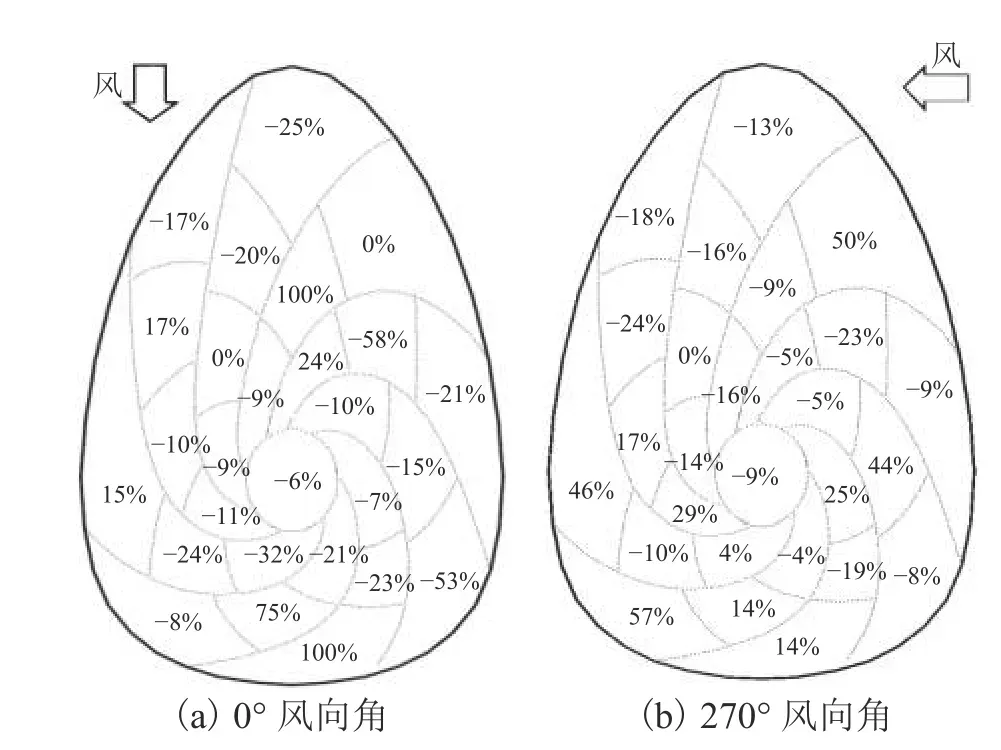
圖10 風荷載體型系數相對誤差Fig. 10 Relative error of wind load shape coefficient

綜上所述，數值模擬結果與風洞試驗結果除在屋蓋正負壓過渡區和尾流區存在較大差異之外，0°風向角時，長軸方向的測點風壓系數的偏差比在± 0.50以內，短軸方向的偏差比在 ± 0.18以內，270°風向角時，長軸方向的測點風壓系數的偏差比在± 0.26以內，短軸方向的偏差比在 ± 0.31以內；0°及270° 風向角下，風荷載體型系數相對誤差均在± 25%以內.

4 裝飾條對屋面風荷載特性的影響

為研究裝飾條對貝殼形屋蓋表面風荷載特性的影響，分別建立了某高鐵站房貝殼形屋蓋的有表面裝飾條和無表面裝飾條的數值風洞模型，并分別進行了數值模擬計算. 通過對各風向角下的風荷載升力系數、風荷載局部體型系數和速度矢量圖的對比分析，探討裝飾條對貝殼形屋蓋風荷載特性的影響.

4.1 風荷載升力系數

對有裝飾條模型采用數值模擬和風洞試驗得到了各風向角下的風荷載升力系數，對無裝飾條模型采用數值模擬計算升力系數. 此處，將風荷載升力系數定義為屋蓋所受豎向風荷載與屋面標準風荷載之比，如式（16）.

式中：βj為第j種情況時的風荷載升力系數，此處j取1、2、3，分別為有裝飾條模型數值計算、有裝飾條模型風洞試驗和無裝飾條模型數值計算，余同；Fj為第j種情況時屋蓋所受豎向風荷載；V為來流風速；A為屋面參考面積.

各風向角下，風荷載升力系數及偏差率見表1.從表中可以看出：有表面裝飾條模型數值計算與風洞試驗結果相比，二者的差異較小，風荷載升力系數偏差率在?7.1%～6.1%之間；有表面裝飾條模型風洞試驗結果與無表面裝飾條模型數值計算結果相比，各風向角下，無表面裝飾條模型的風荷載升力系數要大一些，偏差率在1.5%～22.4%之間，當風向角為90° 和270° 時，由于裝飾條的旋轉方向為阻風向且阻擋面積最大，偏差幅度較大，當風向角為0°和180° 時，二者的差異較小；有表面裝飾條模型數值計算結果與無表面裝飾條模型數值計算結果相比，除180° 風向角下，二者基本相同之外，其余各風向角下，均為無表面裝飾條模型的風荷載升力系數偏大，偏差率在?0.8%～22.4%之間，當風向角為90° 和270° 時，偏差率較大，當風向角為0° 和180°時，二者的差異較小.

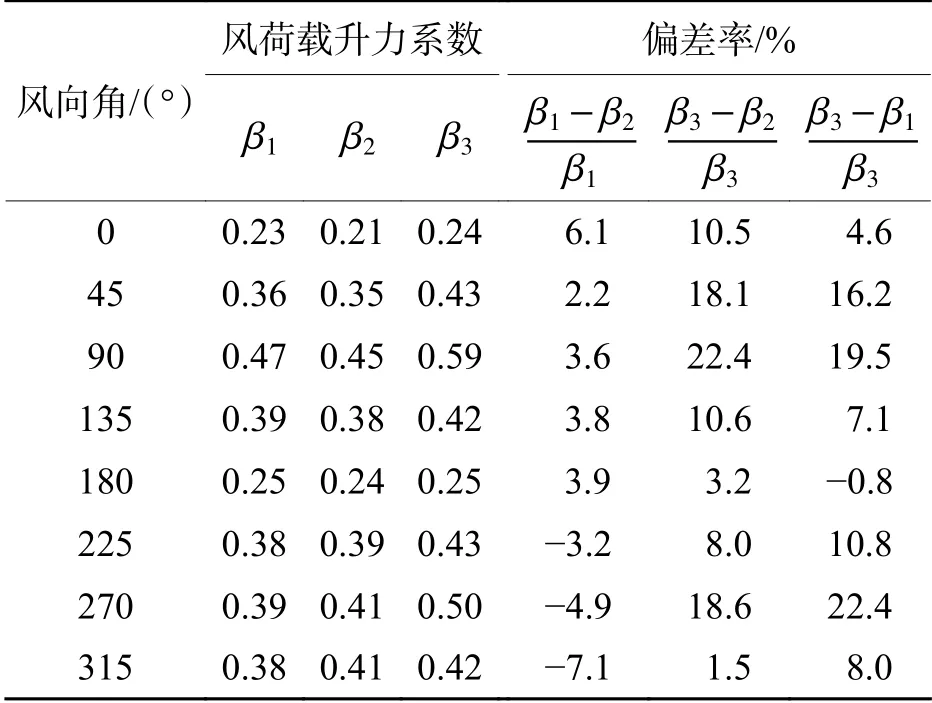
表1 各風向角下的風荷載升力系數及偏差率Tab. 1 Wind load lift coefficient and deviation rate undereach wind direction angle

風荷載升力系數隨風向角的變化情況如圖11所示，從圖中也可以明顯看出：各風向角下，有表面裝飾條模型數值計算結果與風洞試驗結果之間的差異較小，而與無表面裝飾條模型數值計算結果之間的差異隨風向角有較為明顯的變化，當風向角為90° 和270° 時，偏差率較大，當風向角為0° 和180°時，二者的差異較小.

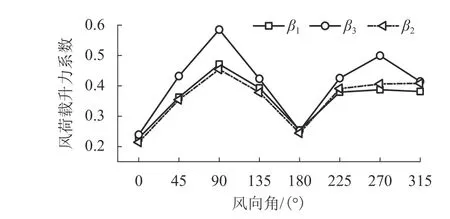
圖11 風荷載升力系數隨風向角的變化情況Fig. 11 Variation of lift coefficient of wind load with wind direction angle

總體說來，有表面裝飾條的貝殼形屋蓋較無表面裝飾條的風荷載升力系數小，說明表面裝飾條對于大跨度貝殼形屋蓋的整體抗風是有利的，這與Letchford等[24]的結論基本一致.

4.2 風荷載局部體型系數

為了解裝飾肋條對屋蓋局部圍護結構風荷載特性的影響，將整個屋面以相鄰4塊ETFE氣枕劃分為一個區塊，整個屋蓋總計有的235個區塊，區塊編號分別為1、2、···、235，區塊總體劃分情況如圖12所示. 風荷載局部體型系數的計算方法與風荷載體型系數的計算方法類似，此處不再贅述.

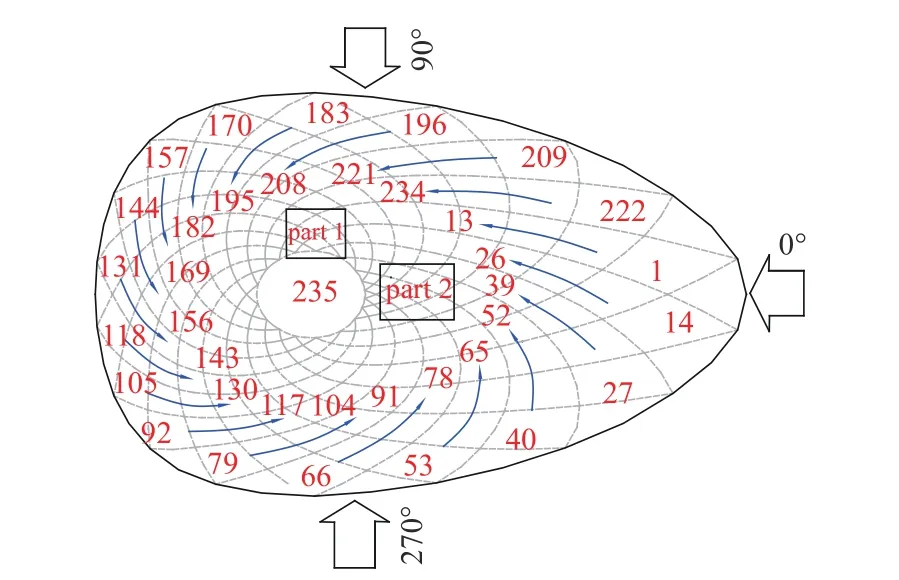
圖12 風向角及細部區塊定義Fig. 12 Definition of wind direction angle and detailed block

采用數值模擬方法分別計算有表面裝飾條模型和無表面裝飾條模型的風荷載局部體型系數（Us1），圖13為典型風向角（0° 和270°）下各區塊的風荷載局部體型系數隨區塊的變化曲線. 從圖中可以看出：裝飾條對風荷載局部體型系數的影響程度與風向角有關，0° 風向角時，裝飾肋條對局部風壓的影響較大，270° 風向角時，裝飾肋條對局部風壓的影響較小. 在迎風面，裝飾肋條對風荷載局部體型系數的影響較小，二者較為接近，越靠近屋蓋頂部二者差異越大. 在兩側繞流區域和尾流區域，有表面裝飾肋條屋蓋的風荷載局部體型系數小于無表面裝飾肋條屋蓋. 同時，無論是正壓還是負壓，有表面裝飾肋條屋蓋的風荷載局部體型系數都要小于無表面裝飾肋條屋蓋.

為了解裝飾肋條對屋面局部風壓的影響程度，定義風荷載局部體型系數偏差比為

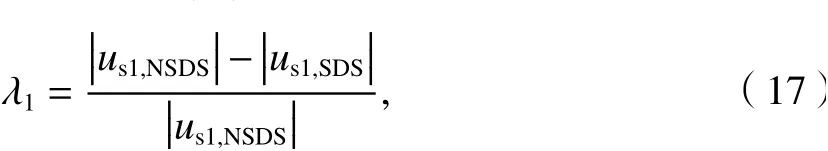
式中：usl,NSDS為無表面裝飾肋條屋蓋風荷載局部體型系數；usl,SDS為有表面裝飾肋條屋蓋風荷載局部體型系數.

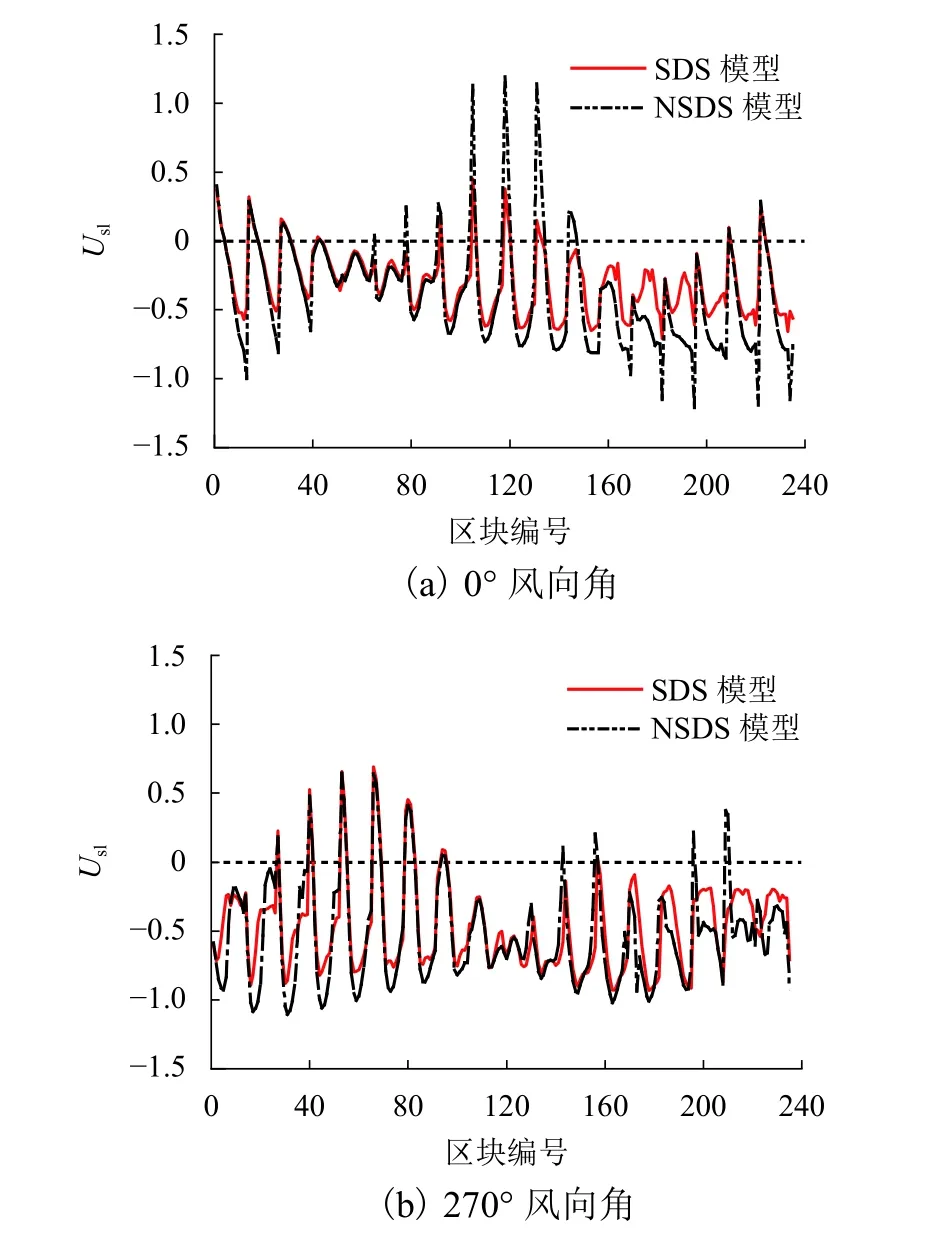
圖13 風荷載局部體型系數隨區塊的變化曲線Fig. 13 Variation curve of local shape coefficient of wind load with block size

圖14為風荷載局部體型系數偏差比隨區塊的變化曲線. 從圖中可以看出：各風向角下，裝飾條可以減少大部分區塊的局部風壓，同時也會使個別區塊的局部風壓增大. 與無表面裝飾肋條屋蓋相比，0°風向角下，設置裝飾肋條可以減小屋面局部風壓50%左右，同時會使得個別區塊的風壓最大增加4.5倍左右，270° 風向角時，大部分區塊的風荷載局部體型系數偏差比在0～0.5之間，個別區塊的風荷載局部體型系數偏差比較大，最大值接近?5.0.

綜上所述，裝飾肋條并未改變大跨度貝殼形屋蓋以吸力為主的風荷載作用機制，與無表面裝飾肋條相比，設置裝飾肋條可以使屋面大部分區域的局部風壓減小0～50%左右，但也會使得屋面個別區域的風壓增大最大達5倍，在對局部附屬構件的設計時應予以重點關注.

4.3 裝飾肋條對屋蓋風荷載特性的影響機理

為深入了解屋面裝飾肋條對貝殼形屋蓋影響機理，本文以屋蓋頂部附近典型區域part 1 （見圖12）為例，分析裝飾肋條對風壓系數分布和風速矢量的影響.

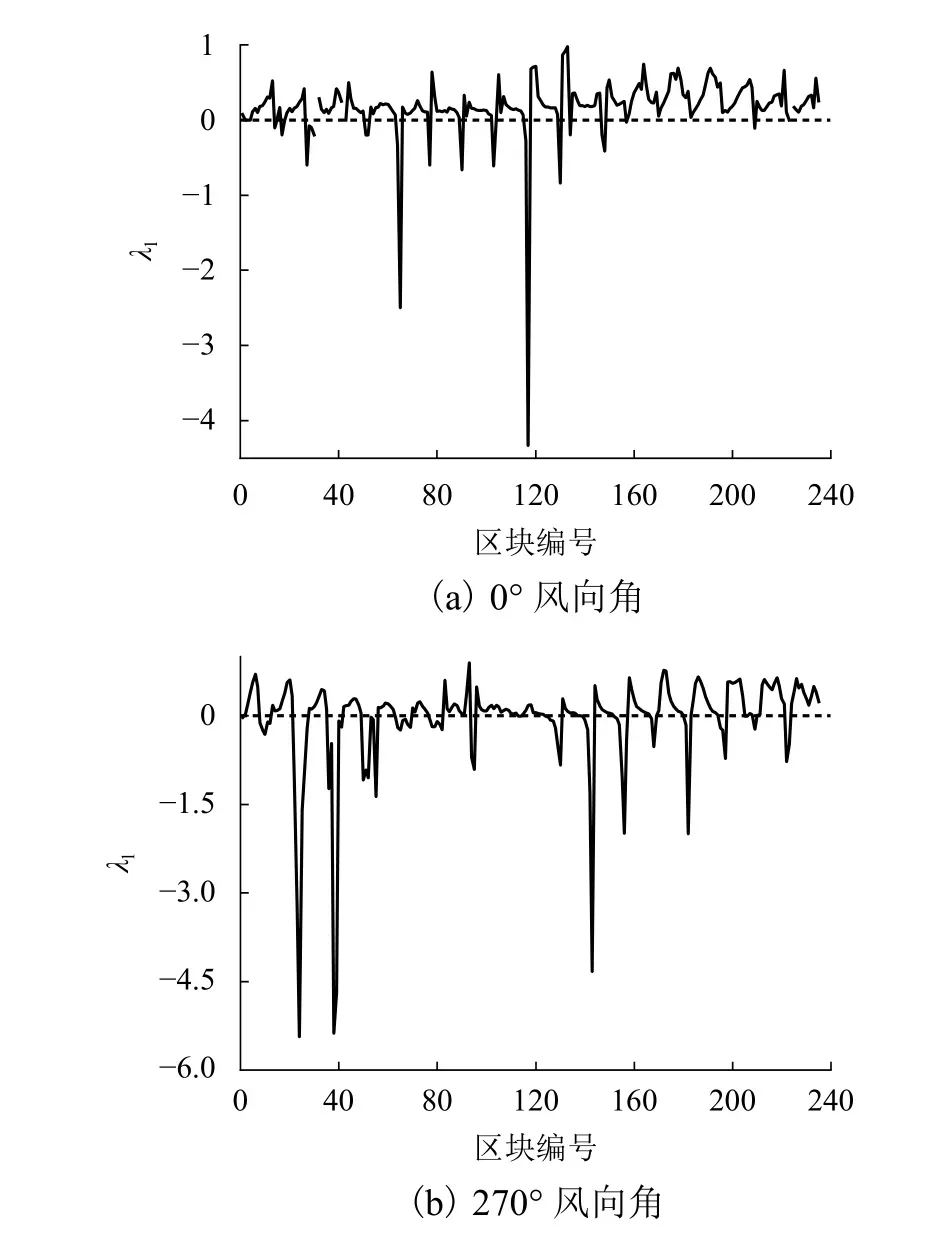
圖14 風荷載局部體型系數偏差比隨區塊的變化曲線Fig. 14 Variation curve of deviation ratio of local shape factor of wind load with block size

4.3.1 局部區域風壓系數分布

圖15為0° 風向角下的屋面part 1的風壓系數分布情況. 從圖中可以看出：在屋面頂部邊緣處，無表面裝飾條屋蓋的風壓系數在?0.70～?0.90，有表面裝飾條時為?0.60，減小風壓15%～33%；帶有肋條區域總體來講是肋條處的風壓系數較大，為?0.80，肋條之間風壓系數較小，為?0.40～?0.60，無表面裝飾肋條的風壓系數為?0.55～?0.70. 圖16為270° 風向角下的屋面part 1的風壓系數分布情況.從圖中可以看出：無表面裝飾條的屋頂風壓系數為?0.24～?0.38，有表面裝飾條屋頂為?0.15～?0.30，風壓降幅在27%～37%；無表面裝飾條的屋面風壓系數為?0.22～?0.34，而有表面裝飾條屋面為?0.10～?0.20，風壓降幅在40%～55%，而帶有裝飾條區域依然是肋條處的風壓系數較大，為?0.40. 出現這種較大差異的原因可能在于裝飾肋條之間存在一定的狹管效應以及肋條對風流的阻擋作用，裝飾肋條的設置會導致肋條自身的局部風壓較大，在設計時務必予以重點注意，同時，又可以降低無肋條區域的表面風壓15%～50%左右，這對ETFE氣枕的抗風是有利的.

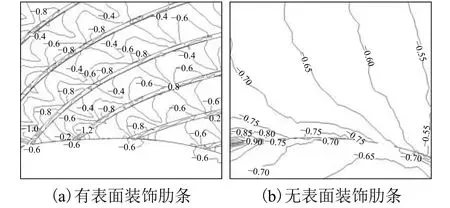
圖15 0° 風向角part 1風壓系數分布Fig. 15 Wind pressure coefficient distribution of part 1 under 0° wind angle

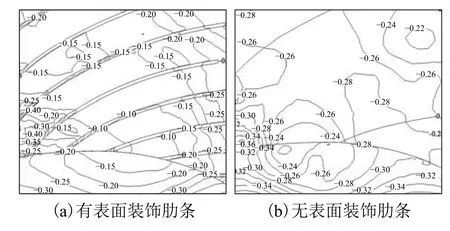
圖16 270° 風向角part 1風壓系數分布Fig. 16 Wind pressure coefficient distribution of part 1 under 270° wind angle

4.3.2局部區域速度矢量分布

圖17為屋面在0° 風向角下part 1區域的屋蓋表面風速示意. 從圖中可以看出：相較于無表面裝飾條屋蓋，裝飾肋條之間具有一定的狹管效應，肋條對風流的阻擋效應致使風流在肋條處有明顯的漩渦產生，這種漩渦可能對風速有放大作用，從而使得肋條處的風壓較高，風壓存在突變現象. 由于裝飾肋條呈螺旋形，風向角對裝飾肋條間的狹管效應以及肋條阻擋效應影響也較大. 0° 風向角下，肋條和屋蓋表面的風流均隨螺旋形肋條的旋轉改變，圖中非常清楚的顯示了裝飾肋條之間的狹管效應及導流作用.

圖17 0° 風向角下part 1速度示意Fig. 17 Velocity vector of part 1 for 0° wind direction angle

圖18為0° 風向角下10 m高度處水平風速矢量圖. 可以看出：有表面裝飾條屋蓋由于裝飾條的存在導致側面來流的分離而在背風面形成小區域尾渦，無裝飾條屋蓋則來流附著屋蓋表面流動，背風面無尾渦形成；圖19為270° 風向角下10 m高度處水平風速矢量圖，兩種模型均在背風面形成對稱尾渦，但有裝飾條屋蓋尾渦區域要大于無裝飾條屋蓋，這是由于此風向角下建筑物側面繞流明顯，而裝飾條的存在加劇了來流分離，從而在背風面形成較大尾渦區.

圖18 0° 風向角下10 m高度處水平風速示意Fig. 18 Horizontal wind speed vector at 10 m height under 0° wind angle

圖19 270° 風向角下10 m高度處水平風速示意Fig. 19 Horizontal wind speed vector at 10 m height under 270° wind angle

綜上所述，表面有螺旋形裝飾條的大跨貝殼形屋蓋表面流體運動復雜，影響其表面的風壓分布的因素眾多，有無裝飾條、裝飾條的布置形式以及來流方向等均會有影響，但有裝飾條屋蓋會降低整體風壓而局部出現小區域高負壓，設置裝飾條對結構整體抗風是有利的，但裝飾條及其周圍區域應加強局部抗風設計.

5 結 論

1） 采用已有試驗數據對有表面裝飾肋條的大跨貝殼形屋蓋的數值風洞模型的可靠性進行了驗證，軸向測點平均風壓系數試驗值與計算值變化趨勢一致，風荷載體型系數相對誤差在 ± 25%以內，風荷載升力系數偏差率在?7.1%～6.1%.

2） 各風向角下，無表面裝飾條模型的風荷載升力系數比有表面裝飾條模型大，最大偏差率可達22.4%，且風向角為90° 和270° 時，偏差率較大，風向角為0° 和180° 時，二者的差異較小，表面裝飾條的設置對于大跨度貝殼形屋蓋的整體抗風是有利的.

3） 裝飾條的設置并不改變大跨度貝殼形屋蓋以吸力為主的風荷載作用機制，與無表面裝飾條相比，設置裝飾條可以使屋面大部分區域的局部風壓減小0～50%左右，但也會使得屋面個別區域的風壓增大2～5倍，局部附屬構件的設計時應予以重點關注.

4） 裝飾肋條之間具有一定的狹管效應，肋條對風流的阻擋效應致使風流在肋條處有明顯的漩渦產生，這種漩渦可能對風速有放大的作用，從而使得肋條自身的風壓較高.