位場向下延拓系數矩陣性質及Barzilai-Borwein向下延拓法

張志厚 ，廖曉龍 ，姚 禹 ，范祥泰 ，路潤琪

（西南交通大學地球科學與環境工程學院，四川 成都 611756）

重磁位場向下延拓技術可以將海平面磁測數據大深度向下延拓至海底，將航空重磁數據延拓至地形線，不僅突出了有用信息，還可以彌補條件惡劣地區重磁場資料的不足，并且重磁位場的向下延拓運算是許多重磁數據處理的核心步驟[1-5]. 此外，重磁位場的向下延拓技術在軍事領域具有非常重要的作用[6-9].

重磁位場向下延拓的主要方法從類型上大體可以分為泰勒級數法[10-13]、等效源法[14-20]、積分迭代法[1-4,21-23]、Tikhonov正則化法[24-29]、Landweber正則化法[26,28,30]、奇異值分解法[26]等.

泰勒級數法的主要缺點是更高階次的導數計算會導致數據的高頻成分被無限放大，曾小牛等[31]對求導的頻譜函數進行了改進，但階次越多誤差也被疊加得越多，最終導致下延誤差反而很大；等效源法的主要缺點是計算時間長，且延拓效果受到“源”的類型、個數、深度及其組合的影響.

位場向下延拓的積分迭代法[21,32]計算效果好，諸多學者研究了其魯棒性等性能[33-36]，該方法在數學上也被稱為對稱核第一類Fredholm積分方程的逐次逼近解法[37]. Tikhonov正則化法相比Landweber迭代法具有最好的綜合下延性能[26,28]. 然而Tikhonov正則化法存在正則化參數的選取問題.

空間域的位場向下延拓實質上是求解一個第一類Fredholm型積分方程，該方程最突出的特性是其“不適定”性. 向下延拓方程離散化后的系數矩陣為實對稱矩陣. 本文首先證明了該系數矩陣為對稱的雙重Toeplitz系統矩陣 （blak-Toeplitz-Toeplitzblock, BTTB）；其次假定在其正定的條件下，采用Barzilai-Borwein （BB）法[38-39]求解該線性方程組，并對迭代步長進行限制，保證了假定系數矩陣為正定情況下算法的收斂性，實現了位場的向下延拓計算，在迭代計算中使用BTTB與向量乘積的快速算法[40]對大數據進行計算，一定程度上節約了計算成本，并對該方法進行了理論模型無噪聲數據與實際資料的檢驗，以及對比分析了該方法的收斂速度與位場向下延拓的積分迭代法的收斂速度.

1 空間域位場向下延拓

假設位場觀測面為笛卡兒直角坐標系o-xyz的水平面 （z=0 ），該平面上的位場為f0(x,y)，計算z=h（h> 0）平面的位場fh(x,y)，且該平面為觀測面以下至場源以上空間（z軸向下）.

根據向上延拓公式，可得

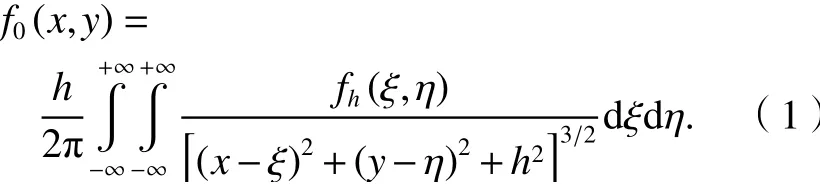
表示成褶積的形式為

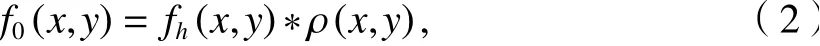
2 位場延拓系數矩陣的性質

陳龍偉等[41]較為詳細地證明了位場向下延拓系數矩陣為對稱的分塊Toeplitz矩陣，本文提供一種簡潔的證明方法. 已知f0(x,y) 通過式（1）求解fh(x,y)即為向下延拓，由于已知場與待求場皆為離散化數據，且f0(x,y) 與fh(x,y)離散化網格規格一致，因此將

式（1）離散化[42]為

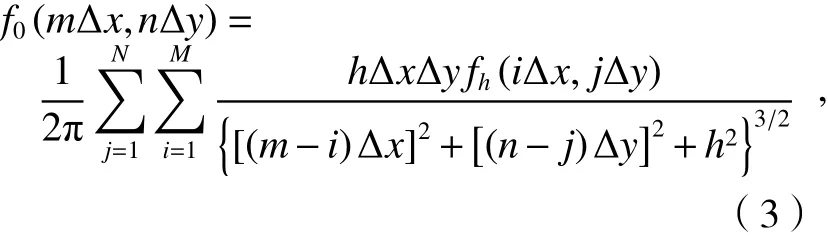
式中：Δx、Δy分別為方向x、y的離散化網格間距；M、N分別為方向x、y的離散化網格點總數，m=1,2,3,···,M，n=1,2,3,···,N.

由于離散化網格間距固定，為了方便表示，將f0(mΔx,nΔy) 與fh(iΔx,jΔy) 分 別 寫 成f0(m,n)與fh(i,j) ，將式（4）中的f0和fh重排為列向量，分別記為

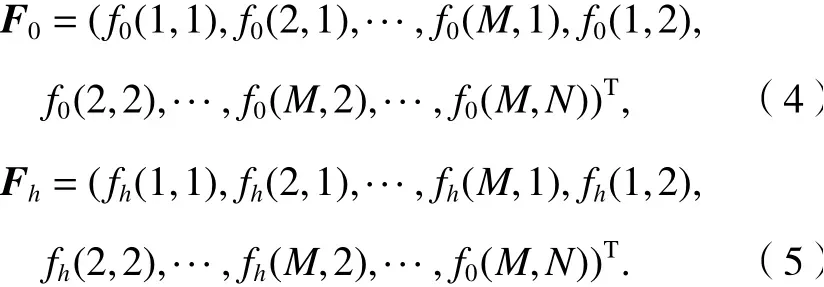
式（4）用矩陣表示為

式中：A為位場向下延拓的系數矩陣.

根據式（4），位場向下延拓的系數為

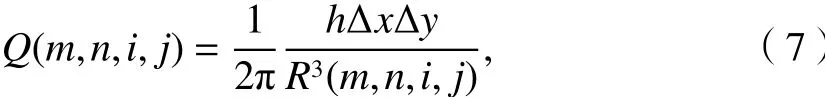
借鑒“格架函數”概念[43]，發現Q也具有平移等效性、互換對稱性，等價關系為

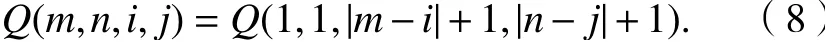
式（8）左右兩端分別代入式（7）即可得證. 根據式（8），4位數組Q(m,n,i,j)的前兩個參量都是常數1，故其可表示為二維數組，即將Q(m,n,i,j)簡記為Q|m?i|+1,|n?j|+1.Q為四維數組，以行列式的形式排列即可得到：

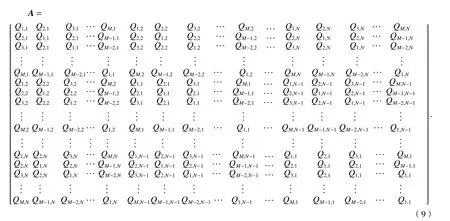
可以看出：A為對稱矩陣，大小為MN×MN，內部包含了N2個分塊的對稱矩陣，大小為M×M，即矩陣A為雙重Toeplitz系統矩陣.

3 BB法

BB法是一種特殊的最速下降法[44]，假設A正定，式（7）采用BB法求解，位場向下延拓BB法的迭代格式為

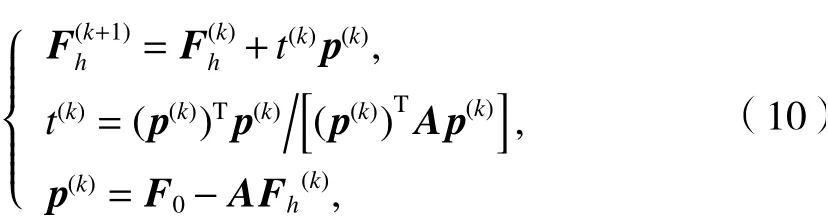
式中：k為迭代次數為第k次向下延拓的計算值；t(k)為第k次的迭代步長；p(k)為第k次迭代待延拓場向上延拓值與已知場的差值向量

迭代停機準則：當 (p(k))Tp(k)<τ，即Cτ 時可停止計算，其中 τ為給定的適當小正數，C為常數，此時

若式（11）中的t(k)為常數時，上述迭代方法即為位場向下延拓的積分迭代法. 而向下延拓BB法相當于變步長的積分迭代法；王順杰等[36]采用不動點原理證明了位場向下延拓積分迭代法的收斂性，但迭代步長的取值范圍在0～2. 因此在求解式（4）時，將其迭代步長約束在0～2范圍內可確保向下延拓BB法的魯棒性. 考慮到迭代過程中必然會存在計算數據量大的問題，采用對稱Toeplitz矩陣與向量相乘的快速算法[40]對式（11）中的和進行計算，有效地提高計算效率.

4 模型試驗

4.1 二維模型

二維模型為無限延伸的水平圓柱體，正演計算兩個不同高度觀測線的理論重力異常，其中觀測線與模型體垂直，對計算結果和收斂速度進行分析.

圓柱體模型的半徑為500 m，線密度 λ=1000kg/m3，模型的中心埋藏深度為3 km. 計算點距為100 m，計算了z=0 和z=2km的理論重力異常. 將z=0理論異常分別采用BB法與積分迭代法向下延拓至z=2km. 理論重力異常與不同方法向下延拓后的結果如圖1所示.

z=2km 理論重力異常的最大值與最小值分別為10.477 × 10?5、0.064 × 10?5m/s2；z=0理論重力異常的最大值與最小值分別為3.492 × 10?5、0.182 ×10?5m/s2. 結果表明：1） 迭代10次BB法計算結果的最大、最小值分別為8.645 × 10?5、?0.015 × 10?5m/s2，積分迭代法計算結果的最大、最小值分別為7.715 ×10?5、?0.164 × 10?6m/s2；2） 迭代50次BB法計算結果的最大、最小值分別為9.542 × 10?5、?0.173 × 10?6m/s2，積分迭代法計算結果的最大、最小值分別為9.132 ×10?5、?0.171 × 10?6m/s2. 由此可見，相同迭代次數下，BB法的計算結果與理論重力異常更為接近.

為了定量地評價本文所提方法的計算精度、穩定性，采用不同迭代次數計算結果的均方誤差來評估其效果，均方誤差為

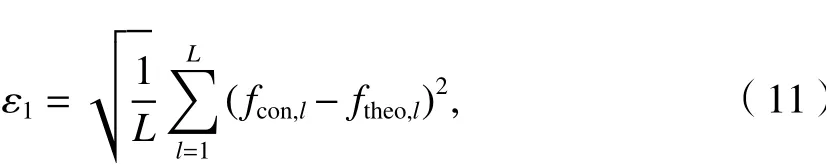
式中：fcon,l和ftheo,l分別為第l個計算點的延拓值和理論值；L為計算的點數.

圖2為位場向下延拓的BB法與積分迭代法在不同迭代次數下計算結果的均方誤差. 可見兩種方法都具有較好的收斂性，但向下延拓BB法的收斂速度更快.

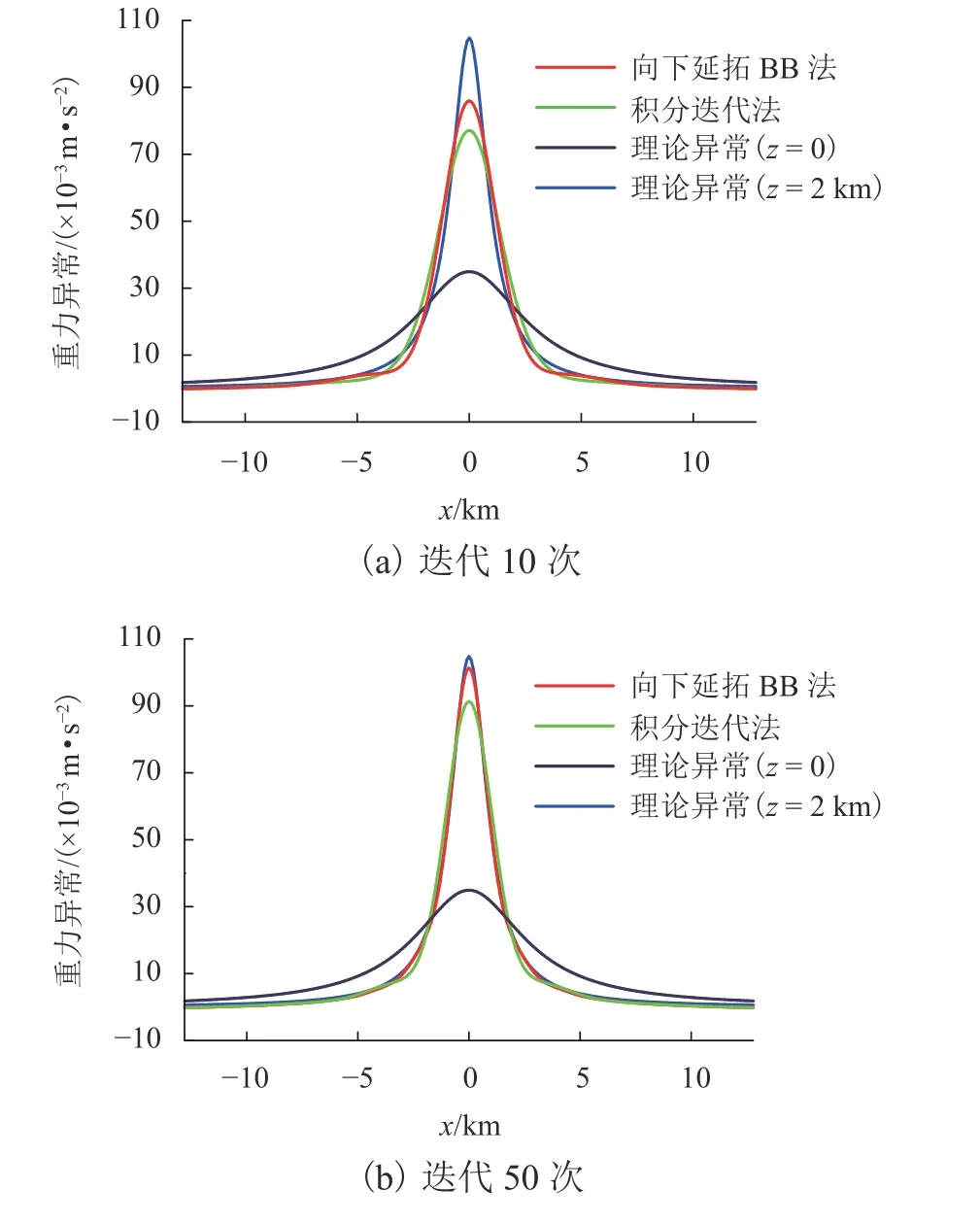
圖1 理論重力異常與不同方法向下延拓結果對比Fig. 1 Theoretical gravity anomaly compared with downward continuation results of different methods

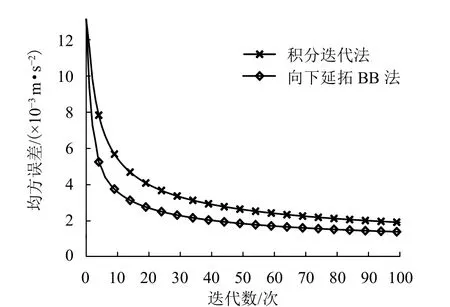
圖2 重力模型計算結果的均方誤差Fig. 2 Mean square error calculated by gravity model

4.2 三維模型

三維模型為組合圓球型磁異常體，通常被用于位場向下延拓效果的檢驗[45-47]. 首先通過正演計算兩個觀測面的磁異常，然后采用不同計算方法將距離場源較遠處的平面磁異常向下延拓至另一平面，通過均方誤差來評估計算效果. 三維組合圓球形磁異常體參數見表1. 表中：(x0,y0,h0)為圓球型異常體中心坐標；r0為圓球異常體半徑；M0異常體磁化強度；I0和A0分別為地磁場傾角和剖面磁偏角；I′和A′分別為異常體磁化強度的傾角和磁北夾角. 根據圓球型磁異常體的正演計算解析式[48]，分別計算兩個不同觀測面上的磁異常，如圖3所示，其中虛擬觀測區網格點個數為401× 401，Δx與 Δy都為50 m.

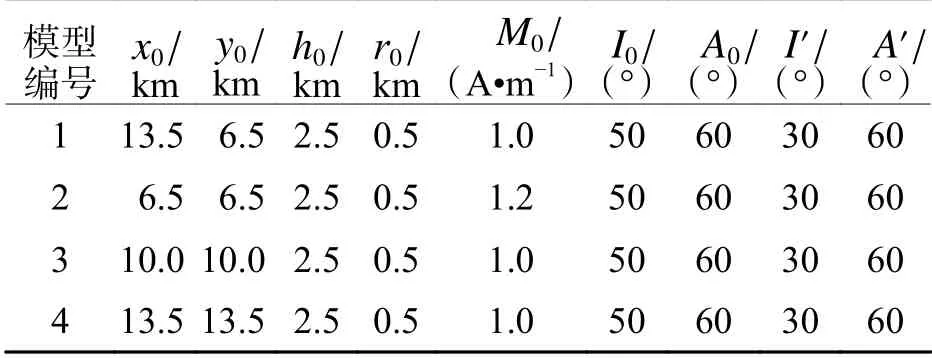
表1 三維組合圓球型磁異常體參數Tab. 1 Magnetic anomaly parameters of 3D combination sphere

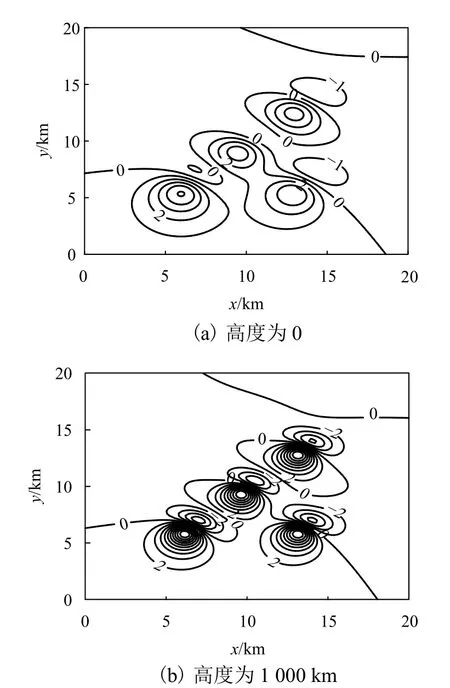
圖3 不同高度面上的磁異常等值線（單位：nT）Fig. 3 Magnetic anomaly isolines at different planes (unit： nT)

將位于z= 0高度的理論磁異常分別采用BB法以及積分迭代法下延至z= 1 km的平面，計算結果見圖4所示. 其結果除了邊部的零等值線略有偏差，其余部分都與理論場（圖3（b））高度吻合.

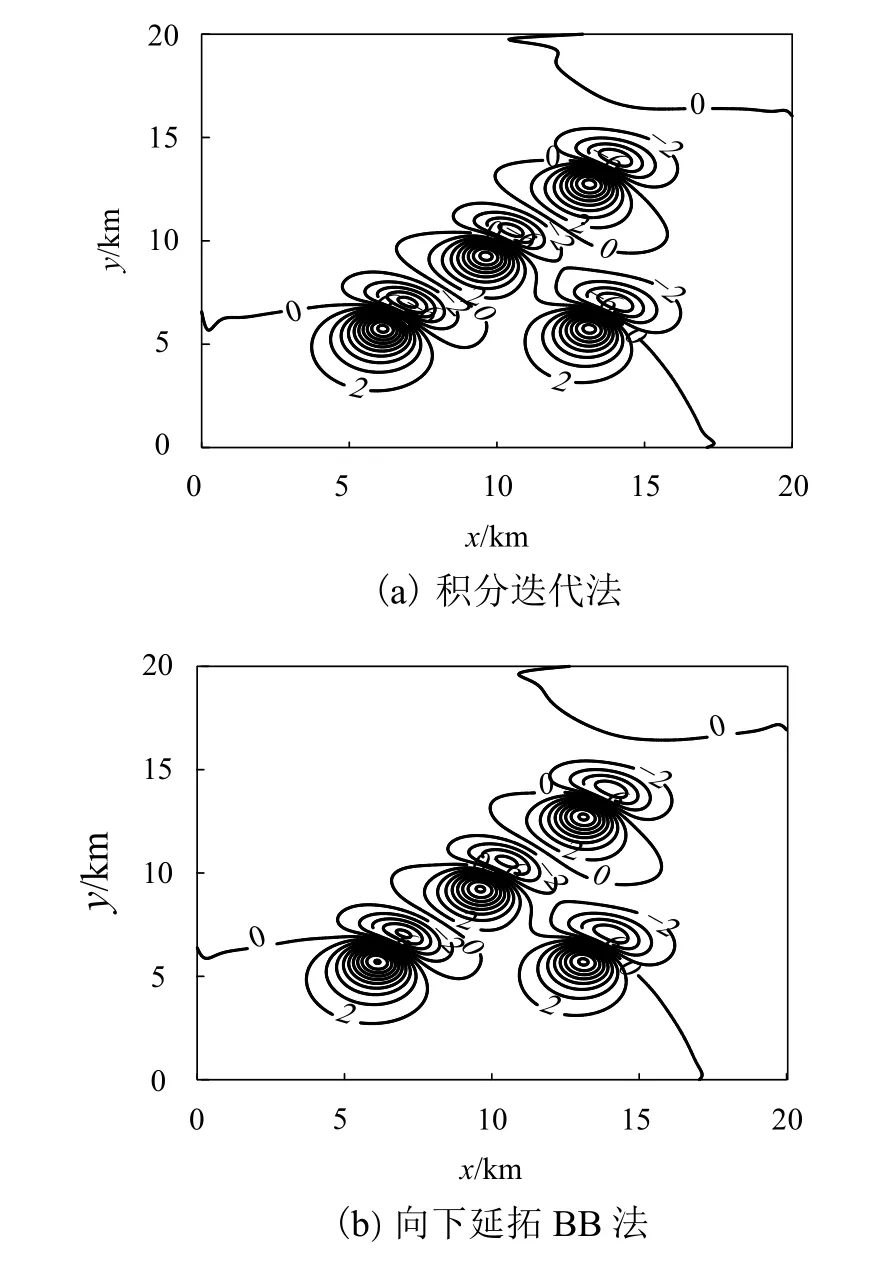
圖4 理論磁異常向下延拓后的計算結果（單位：nT）Fig. 4 Calculation results of theoretical gravity anomaly after downward continuation (unit： nT)

兩種方法計算結果的均方誤差如圖5所示，可以看出：隨著迭代次數的增加，均方誤差都在急劇衰減，BB法相比積分迭代法的收斂速度更快；在相同迭代次數的情況下，位場向下延拓BB法的計算結果的精度高于積分迭代法；同一收斂精度下，當均方誤差在0.4 nT以下時，BB法需要迭代次數15次，而積分迭代法需要迭代35次以上，可見向下延拓BB法的計算速度提高了2倍.

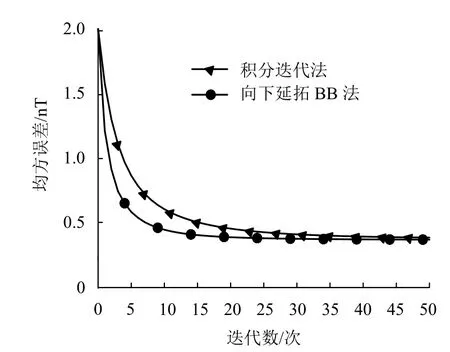
圖5 三維磁場模型計算結果的均方誤差Fig. 5 Mean square error calculated by3D magnetic field model

此外，隨著迭代次數增加，位場向下延拓BB法與積分迭代法的計算結果精度趨近，兩種方法的本質都是迭代法，迭代法求解反問題時都會出現所謂的“半收斂”現象[44]，即在迭代的早期階段，估計解可以得到很好的改善，但其長期行為會出現“飽和”效應，甚至會走向無序[49-50]，故而兩種方法的計算精度極有可能會越來越相近.

5 計算速度

在主頻2.30 GHz、內存1024 MB的計算機上，1024 × 1024個數據向下延拓迭代50次，BB法計算時間約為130 s. 另外，一般情況下依據經驗取一定的迭代次數作為停機準則，BB法相比積分迭代法只需要較少的迭代次數便可達到相同的計算精度.

6 實際資料檢驗

通過某銅鐵礦區實測網格化磁異常資料來評估下延計算效果，如圖6所示. 圖6（a）為已知實測的網格化磁異常，點距為50 m. 將該異常向上延拓10倍點距（向上延拓方法采用快速傅里葉變換方法），其結果如圖6（b）所示. 隨后再將該高度上的異常分別采用BB法與積分迭代法向下延拓500 m至原始高度，其結果如圖6（c）、（d）所示（兩種方法迭代次數相同），計算結果都與圖6（a）基本一致.

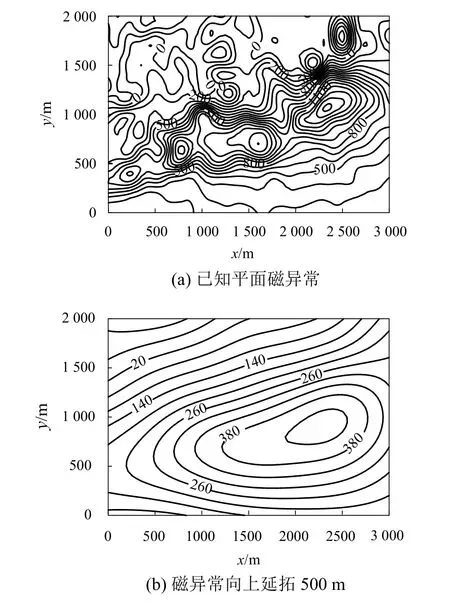
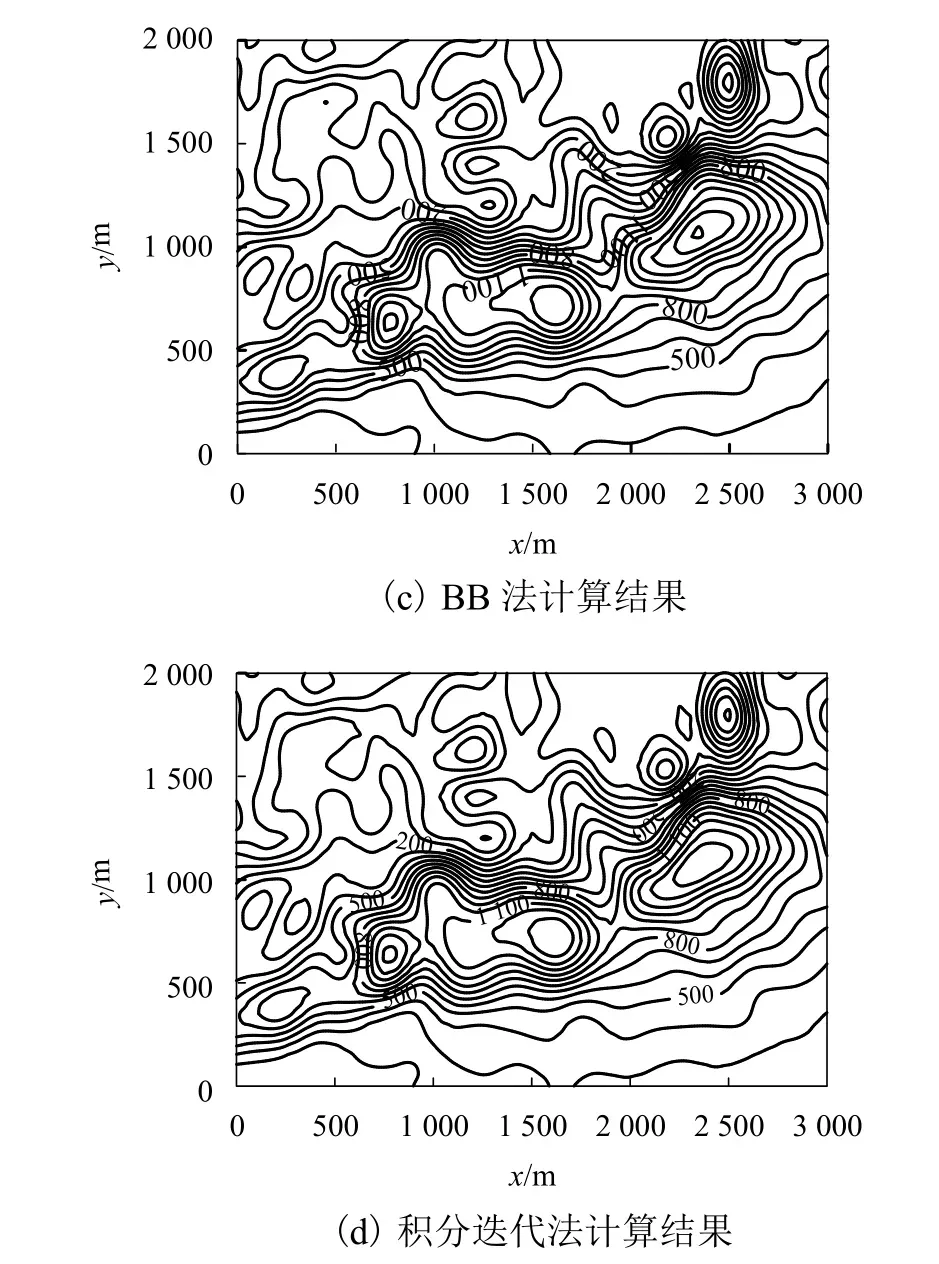
圖6 實例驗證（單位：nT）Fig. 6 Validation by measured data (unit： nT)

原始場的最大、最小值分別為1518.3、?669.2 nT.對應的，向下延拓BB法計算結果的最大、最小值分別為1507.7、?640.7 nT，積分迭代法計算結果的最大、最小值分別為1497.3、?623.5 nT. 用式（11）計算BB法和積分迭代法下延結果的均方誤差分別為24.4 nT和29.7 nT. 相比原始場的最大、最小值，兩種方法的均方誤差都較小，但BB法的精度更高.

為了進一步評價兩種方法的計算精度，采用平均相對誤差 ε進行評估，如式（13）所示.

用式（13）計算本文所提BB法和積分迭代法的平均相對誤差分別為6.1%、7.7%，可見在實際應用中本文所提方法的效果優于積分迭代法.

7 結 論

1） 本文首先證明了位場向下延拓的系數矩陣為對稱的雙重Toeplitz系統矩陣，該性質可為今后的位場數值模擬節省成本.

2） 實現了一種位場向下延拓的計算方法，即位場向下延拓的BB法，該方法主要優點的計算精度高、速度快. 相比普遍采用的Tikhonov方法，文中方法不存在正則化因子的選擇問題.