基于MVTV Copula方法的多風電場電力系統經濟調度分析

李 奇 ，潘俞如 ，邱宜彬 ，陳維榮

（西南交通大學電氣工程學院，四川 成都 610031）

就不包含風電場的電力系統而言，系統中引入的不穩定因素較少，此時的經濟調度方案制定起來較為容易. 隨著國家對風力產業的重視與相關研究的發展，引入電力系統中的風電場數量逐漸增加，系統中涉及的不穩定因素也隨之增多，經濟調度策略的制定變得越來越困難 然而不當的經濟調度策略可能使電力系統運行成本增大，嚴重時甚至會引起電力事故，因此必須對接入風電場或其他新能源的[1].電力系統進行經濟調度研究，這是確保電力系統穩定、經濟運行的重要措施[2].

以往的經濟調度分析主要側重于風力發電的隨機性，對風電出力相關性考慮較少. 近期有許多專家學者開始進行考慮風電出力相關性的經濟調度研究[3]. 鑒于電力資產之間非線性的的動態相關結構，文獻[4]采用對上、下尾部相關性敏感的時變SJC Copula （symmetrized joe clayton Copula）函數描繪電價序列間的相關性，以此擬合電價序列；為了最大程度上描述風電場機群的風速序列的相關性，建立由多種Copula函數組成的混合Copula風電場出力模型，相較于只采用某一種Copula函數構成的模型更切合實際[5]；文獻[6]通過采用3種時變Copula函數分析兩風電場出力數據并獲得擬合模型，通過與靜態Copula函數生成的出力模型對比，證明時變Copula函數對多風電場的相關性擬合精度更高；文獻[7]采用Gumbel Copula函數建立考慮相關性的兩風電場聯合出力模型，并基于該模型采用柔性負荷調峰方法進行隨機經濟調度.

需要指出的是，以上文獻均認為所描述的相關性模型在研究時段內是不變的. 而事實上，考慮時間波動給相關性帶來的影響更符合實際情況，因此Patton提出了可以有效反映相關性內部變化的時變Copula[8]，其準確度在金融、股票市場等相關性研究的問題中均取得了較好的驗證. 除此之外，大部分文獻僅就兩維風電出力數據進行研究，這并不能滿足當下多風電場并網的現狀. 實際中的多維風電出力分布存在隨機性，且不同地區具有不同的特征，如若仍利用兩維變量相關性分析方法分析多維風電出力數據的相關性，則模擬數據會具有明顯的對稱性，這與實際情況不符，偏離實際的數據又會在分析問題與應用時產生更大誤差，后果嚴重者甚至危及電力系統穩定運行與設備安全[9]，因此有必要探索接入多個相關風電場的電力系統經濟調度.

從此角度出發，本文提出MVTV Copula （mix vine time-varying Copula）方法對電力系統進行考慮多維風電出力相關性的經濟調度研究. MVTV Copula方法是基于藤結構與動態、靜態Copula建立的多維變量相關性分析方法，對數據分場景后得到對應的最優Copula函數，并采用混合藤結構建模得到一日內的典型隨機場景. 為驗證所述方法的有效性，采用IEEE-30節點系統，并結合我國某地區的風電歷史出力數據進行研究，分別建立不考慮風電出力相關性的隨機場景，以及依據所述MVTV Copula方法的考慮多風電場出力相關性的隨機場景. 然后再以預測場景下的煤耗費用和隨機場景下的再調度費用最小值為目標，利用回溯搜索算法（backtracking search algorithm，BSA）[10]求解目標函數約束內最優解及其對應調度方案，并通過考慮風電出力相關的經濟調度目標函數值、不考慮風電出力相關的經濟調度目標函數值與實際風電出力數據經濟調度目標函數值的對比分析，對所提出經濟調度方法與相關性建模方法的有效性進行驗證.

1 Copula理論

1.1 概述

Copula函數由Sklar定理推導而來，Sklar認為，必然存在一個函數能將二維隨機變量所對應的聯合分布函數結合起來. 已知n維隨機變量X=(X1,X2···,Xn)，F1,F2,···,Fn為各變量對應的邊緣分布，F為所有變量的聯合概率分布函數，則必有一個Copula函數C使得式（1）成立.

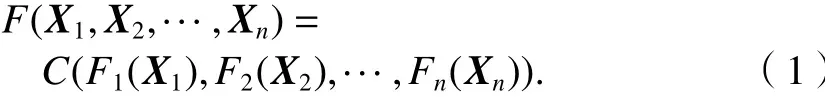
Copula函數對變量的邊緣分布和相關性先后進行建模，在此基礎上構造多元隨機變量的聯合概率分布，是一種可以簡便、清晰地描述數據相關性的計算方法. 常見的Copula函數包含正態Copula函數、Guassian Copula、t-Copula和Gumbel Copula、Clayton Copula、Frank Copula. 由于每種Copula函數的參數性質與計算方式均不同，因此對應不同的相關性結構，這就要求在對二維變量相關結構進行建模時必須選擇對應的最優Copula函數.

1.2 時變Copula函數

時變Copula函數在靜態Copula函數的基礎上考慮時間變化給相關性帶來的影響，認為涉及參數服從與時間相關的動態方程，再通過相關系數與參數之間的映射關系，從而建立參數的動態計算方程.若以正態函數為例并記C為分布函數，u=(u1,u2,···,un)和v=(v1,v2,···,vn) 為相關變量，φ?1(?)表示正態分布的反函數，s、r為分布函數的相關變量，θ 、ρN,t分別為靜態與時變相關系數，后者由對應的時變系數方程求得，其下標N代 表Normal Copula，t為時刻. 靜態與時變Copula函數的具體表達式分別如式（2）、（3）所示.

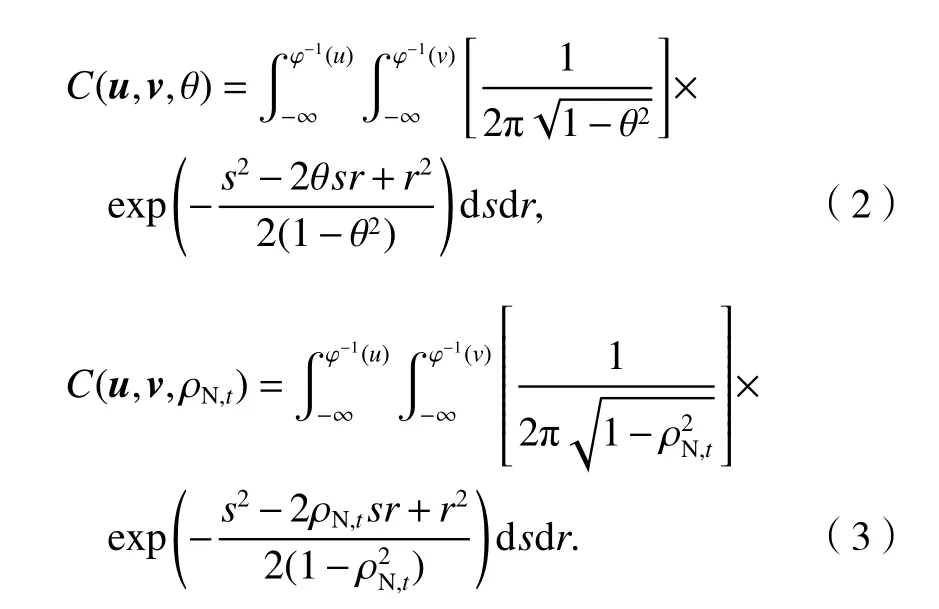
1.3 藤Copula模型

僅單純采用Copula函數法考慮多維風電出力之間的關系時，其相關性描述僅限于兩維變量. 為打破數據維度對Copula函數的限制，有學者提出結合藤結構與Copula函數，采用pair-Copula對多維變量相關性進行分析[11]，該模型先拆分多維變量并通過Copula理論得到兩兩變量之間的相關性，再結合聯合概率分布函數求解. 本文采用C藤（正則藤）和D藤分析數據結構. 當多變量中某個變量與余下變量均具有較強相關性，且整個數據的相關性結構呈現星型放射狀時，C藤結構具有較高精度[12]；D藤模型則具有平鋪式結構，可以更好地描述兩兩變量相關程度高的數據相關性[13]. 在進行藤Copula模型建模時，選擇適應其相依結構的藤結構有助于提高相關性分析精度.

2 基于MVTV Copula方法的隨機場景獲取方法

受限于預測技術，風電出力還無法實現精確預測[14]，但實際情況下的風電有功出力數據符合風電出力的隨機分布[15]，對于這一過程可以用隨機場景來刻畫. 本文為獲取更貼近實際的多風電場出力隨機場景，提出先利用混合藤結構與多種Copula函數構建多維風電出力模型，再在此基礎之上利用蒙特卡洛抽樣和場景縮減法獲取典型隨機場景. 所述基于MVTV Copula方法的隨機場景獲取方法具體如下：

1） 確定最佳聚類參數

統計歷史數據中一天內同一時刻的風電出力數據，由此將一段時期內的歷史風電出力劃分成24組，利用K-means聚類法分析每組數據，并依據中心值進行分場景. 針對傳統K-means方法聚類參數需要根據經驗值人為設定，不能根據數據的不同自適應選取最優聚類參數的問題，本文利用基于密度的聚類數確定（density based index，DBI）法[16]計算幾種聚類數對應的DBI值（D），以此指導K-means聚類方法選取最優聚類參數，如式（4）所示.

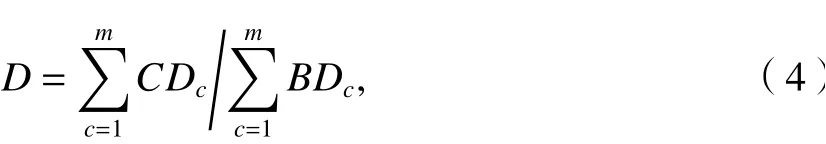
式中：m函數總數；B為類邊緣密度；C為類中心密度；Dc為第c類聚類數對應的DBI指標.

然后再根據最佳聚類數對待分析數據進行聚類劃分.

2） 確定最優Copula函數

以第一組數據（即歷史風電出力數據每日時刻01：00的風電出力數據）為例，分別選擇各組聚類結果對應的最優Copula，其中靜態Copula函數的最優參數均由最大概似估計確定（具體實施可以使用MATLAB自帶copulafit函數完成，在此不做贅述），時變最優參數由對應的時變方程確定[17]. 最優函數類型則根據赤池信息（Akaikein formation criterion，AIC）法計算各備選Copula函數和經驗Copula函數的AIC值，具體計算方式如式（5）.

式中：k為擬合模型的參數個數，其大小反映了模型的復雜程度；L為似然函數，其大小反映了模型擬合度.

時變Copula函數對應的復雜程度雖然較高，但AIC法會引入懲罰系數提高擬合度. 從多個擬合模型中判斷最優模型時，一般較小AIC值對應的模型對應較高的擬合精度.

3） 獲取采樣點

基于以上理論基礎，多維變量的采樣點獲取方式可以概括如下：

步驟1利用MATLAB自帶unifrnd函數模擬生成1組M×N（數據個數 × 維數）均勻變量z，z=(z1,z2, ···,zN)；

步驟2令第1維待求變量u1等于步驟1中的第1列，即u1=z1；

步驟3根據

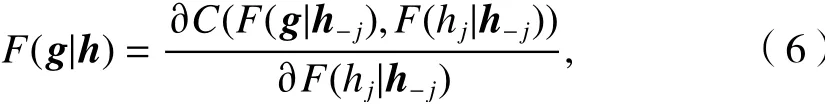
第2維待求變u2可利用式（7）來計算.

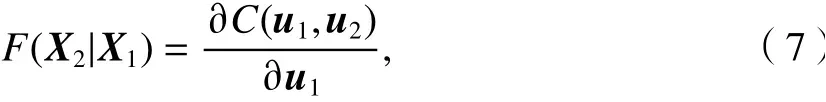
式（6）、（7）中：g、h分別為樣本數據中不同維度的采樣點向量；hj為h中的第j個變量；h?j為h去除hj后的向量；Xi= (ui,vi).

計算時z2為步驟1生成，C(u1,u2)表示u1、u2在對應Copula函數處的函數值，可以通過copulacdf函數計算. 對等式（7）右邊求解，加一個while循環，循環內采用二分法求解u2，直至等式右邊計算出來的數據和左邊相差很小時結束，此時隨機出來的u2即為所求模擬數據.

步驟4令Zi為Xi對應的采樣點，則利用

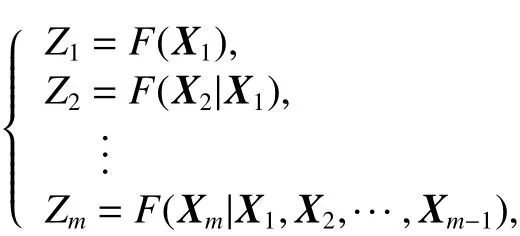
進行迭代求解后續維數模擬數據.

4） 確定最佳藤結構本文選取CvM （cramer von mise）距離（dCvM）來作為模型模擬效果評判指標，通過對比不同藤結構建模結果對應指標值來判斷藤結構模擬效果的好壞，從而完成最優藤結構的選取工作，具體實施方式如式（8）所示[17].

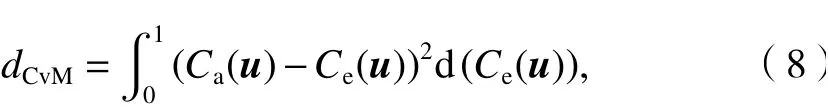
式中：Ca(?)與Ce(?)分別為各備選Copula函數與經驗Copula函數的聯合分布函數值.

最后選取最小的CvM距離所對應的藤結構為該類數據的最優藤結構.

5） 獲取典型隨機場景

上述第 4）步所確定的最優藤結構對應的隨機場景即為所求隨機場景，但因其數量一般較多，所以有必要對所獲取的隨機場景進行相應場景削減以獲取典型隨機場景，本文采用根據距離進行場景削減的同步回代法完成隨機場景的獲取[18]：

步驟1對待分析對象進行場景初始化，利用場景生成方法隨機抽取S個場景，其中各生成場景s（s∈S）相應的概率為

步驟2獲取兩兩場景的歐氏距離，具體表達為

步驟3利用概率與歐式距離進行場景縮減步驟，獲取與場景s相距最近的場景s′，并使用s′代替s，概率距離計算方式如式（9）.

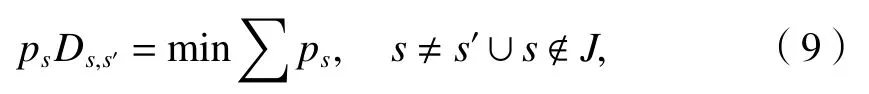
式中：Ds,s′為場景s和s′的歐氏距離；J為所有被削減的場景的集合，其概率修正方式為

式中：ps′為場景s′ 的概率.

步驟4重復步驟2與步驟3，削減至預定的保留數目即可停止.

重復進行以上建模步驟24次，將24次典型隨機場景進行組合，即可獲取一日內的典型隨機場景.

3 考慮風電出力相關性的電力系統經濟調度模型

3.1 目標函數

鑒于風電場正常運行期間所需的運行費用較低[19]，本文在建立電力系統經濟調度目標函數時忽略風電場的運行成本，僅考慮常規的火電機組（以下簡稱機組）在運行期間的煤耗費用以及在隨機場景下的再調度燃料費用作為目標函數（f），如式（11）.

式中：fy為電力系統在預測風電場出力場景對應的機組燃料成本；fw為隨機場景對應的電力系統再調度費用.

對于fy來說，其燃料成本與機組的發電量呈二次函數關系，具體函數形式如式（12）.

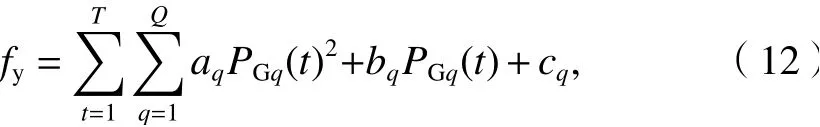
式中：T為一個調度周期內總共包含的時間；Q為電力系 統 中包 括 的機 組 的個數；PGq(t) 為 在時刻t機組q的輸出功率；aq、bq、cq為機組q的煤耗費用價格系數，由機組本身性質決定.

對于fw，其具體表達式為

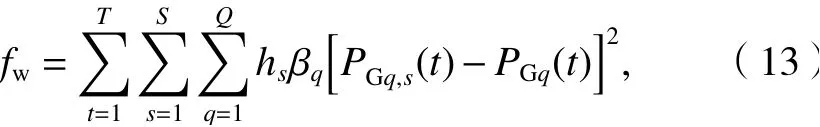
式中：hs與 βq分別為各個隨機場景對應的概率與機組q的再調度費用；PGq,s(t) 為場景s下時刻t機組q的功率.

3.2 約束條件

在進行經濟調度研究時，必須考慮實際情況對經濟調度模型的約束限制，只有這樣才能獲取符合實際情況的調度結果. 除了機組出力限值約束和機組爬坡約束外，還包括系統功率平衡約束. 各約束條件表達如式（14）[20-21].

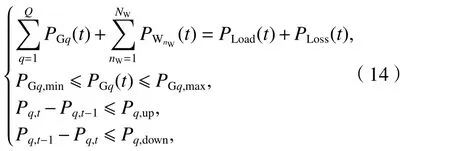
式中：NW為系統中接入的風電場的總數；PWnW(t)為第nW個風電場在時刻t輸出的有功功率；PLoad(t)以及PLoss(t)分別為系統在時刻t的系統負載以及系統網損；PGq,min、PGq,max分別為機組q的有功功率下限、上限；Pq,t和Pq,t?1分別為機組q于時刻t和時刻t?1發出的有功功率；Pq,up和Pq,down分別為最大上升功率和最大下降功率.

4 算例分析

為驗證所述基于MVTV Copula方法的電力系統經濟調度方式的有效性，本文借助IEEE30節點系統對所述方法進行驗證，風電出力原始樣本取自我國某地域3個毗鄰風電場的歷史數據. 其中，風電接入節點分別為8、16、21節點，常規機組接入節點分別為1、2、13、22、23、27節點，調度間隔取1 h. 所述IEEE30節點的拓撲圖如圖1所示[22-23].

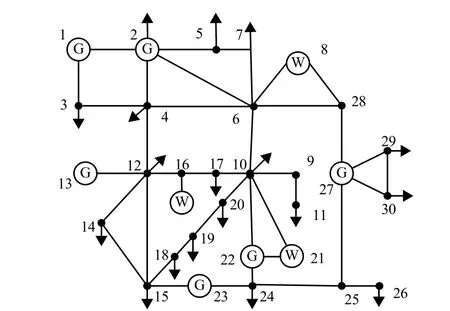
圖1 仿真系統拓撲Fig. 1 Topology of simulation system

因實際運行中負荷曲線一般較為固定，所以算例中不考慮負載曲線的預測，而僅對調度周期內的風電場出力數據進行預測. 算例中使用2012年4月某天的風電實際出力及預測出力為數據進行經濟調度分析，各風電場實際出力曲線及預測出力曲線如圖2所示.

鑒于同一地區氣候條件一般不會發生較大改變，所以本文利用該地區歷史同期數據來構建2012年4月某天不同時刻的風電出力MVTV Copula模型.以01：00時刻風電出力數據的MVTV Copula模型為例，首先利用DBI指標獲取各模型的最佳分類數目，具體操作過程中將K-means聚類參數分別設置為2～14，并選取DBI指標最大的聚類方案確定多維數據的最佳聚類數，所得結果如圖3所示.

從圖3可以看出：根據DBI指標所確定的最佳聚類數為5類，據此對待分析數據各聚類結果分別進行最優藤結構及最優Copula判別，備選靜態Copula函數有：Gumbel Copula函數、正態Copula函數、Frank Copula函數、Clayton Copula函數與t-Coopula函數；備選時變Copula函數有：時變Gumbel Copula函數、時變正態Copula函數與時變SJC Copula（symmetrised Joe Clayton Copula）函數. 所得各參數詳細情況如表1所示.

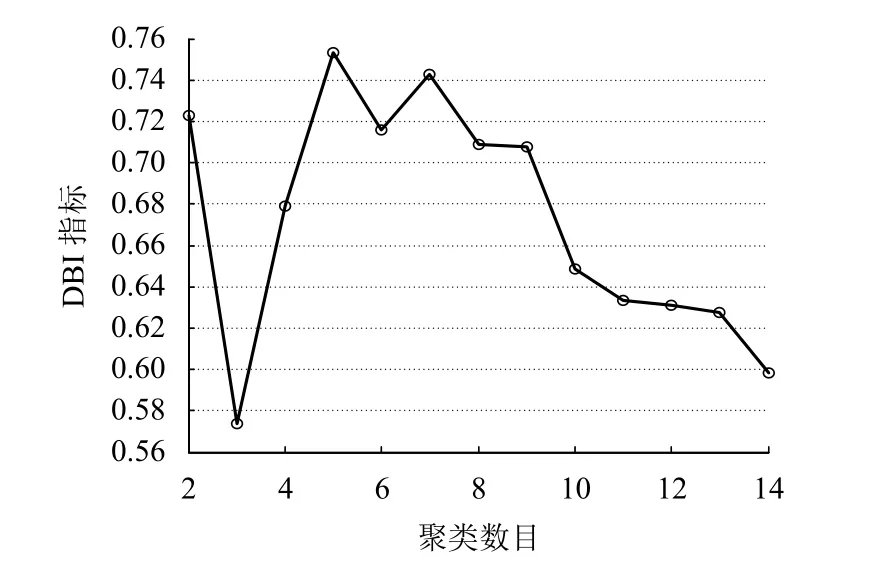
圖3 DBI指標與場景數關系Fig. 3 Relationship between DBI index and scenario number

表1 各場景下最優藤結構及最優參數Tab. 1 Optimal vine structure and optimal parameters for different scenarios

同時，為了更加直觀地反映混合藤結構能在模擬多風電場相關性建模中相較孤立的藤結構獲取更高的準確性，本文仍采用AIC值作為模型與原始數據接近程度的衡量標準，采用混合藤與兩種孤立藤結構的AIC值對比，如表2所示.

表2 采用混合藤與孤立藤結構的AIC值對比Tab. 2 AIC values of mix vine and isolated vine structures

在獲取最佳聚類數和最優Copula函數的基礎之上，利用采樣方法獲取24 h內不同時刻風電出力的720個隨機場景，此時按照同步回代削減法可獲取若干典型隨機出力場景. 本文中典型隨機場景的數量定為10個，具體分布如圖4所示.

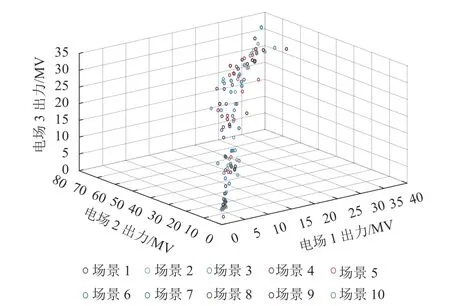
圖4 基于MVTV Copula模型的典型隨機場景Fig. 4 Typical random scenarios based on MVTV Copula model

由圖4可以看出：基于MVTV Copula方法生成的多風電場擬合數據基本分布在坐標軸對角線附近，說明所模擬的風電數據表現出同增同減的正相關特性，該分布較為符合實測相鄰風電場實測出力數據情況. 而圖5所示為不考慮風電出力相關性的隨機場景，風電數據則分布較為零落，未表現出明顯分布特征，與實際相鄰風電出力數據分布差別較大.根據以上兩類典型隨機場景進行電力系統經濟調度研究，采用BSA算法進行求解，分別計算相應的再調度費用，如表3所示.

由表3可以看出：雖然不考慮風電出力相關性的系統再調度費用估計值小于考慮風電數據相關性的經濟調度方式，前者僅為實際調度費用的43.6%，后者為實際調度費用的82.0%，但不考慮相關性所得結果卻與實際情況存在較大偏差，而考慮相關性則較為接近實際調度結果. 這是由于實際的風電數據之間存有一定正相關性，某一個風電場的出力數據增大將大大提高其余風電場的出力數據增大的概率，考慮風電出力相關性的經濟調度方式一定程度上能夠反映這種相關性，得出更貼合實際狀況的分析結果. 考慮風電出力相關性時各典型隨機場景下不同時段常規機組出力和風電出力總和曲線以及負荷曲線如圖6所示.

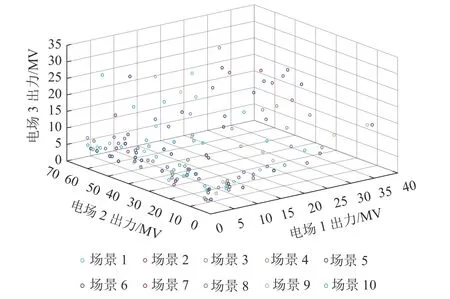
圖5 不考慮相關性的典型隨機場景Fig. 5 Typical random scenarios ignoring dependence of wind outputs

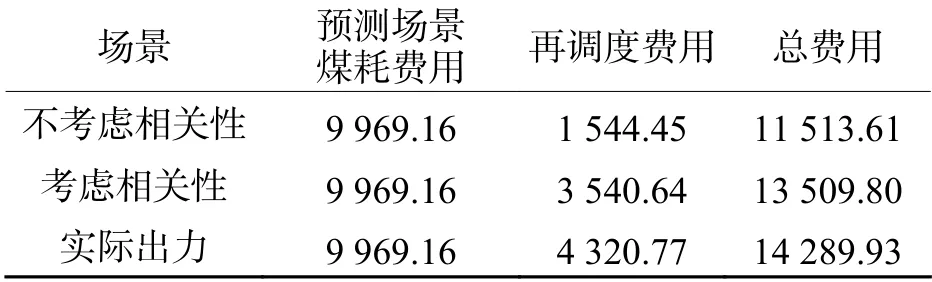
表 3 兩類典型隨機場景情況調度費用對比Tab. 3 Economic dispatch results of two typical random scenarios USD

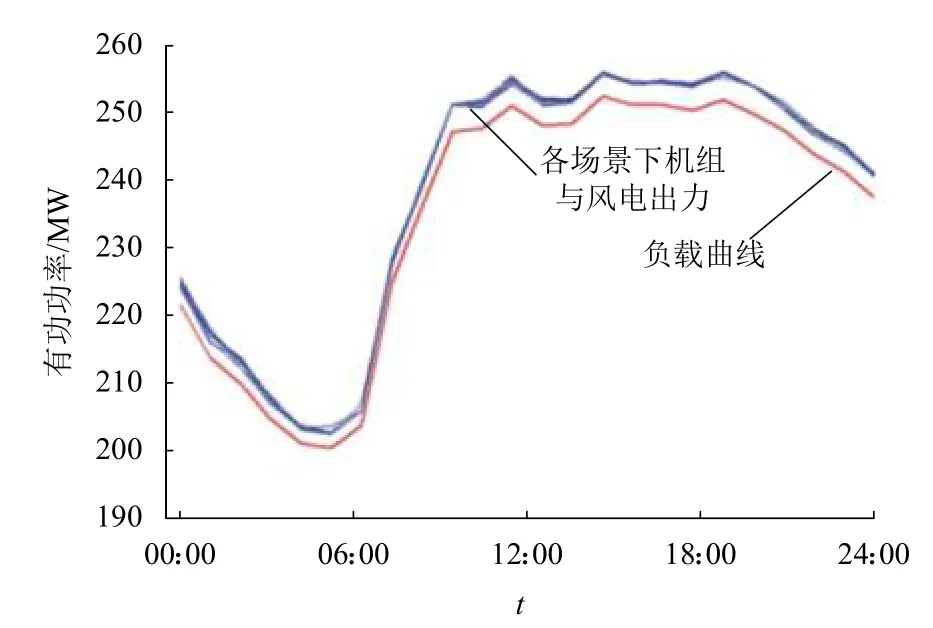
圖6 負載曲線及各場景下機組和風電總出力曲線Fig. 6 Load curve and total output curve of unit and wind power output under different scenarios

從圖6中可以看出：對于所述10個典型隨機場景，利用BSA算法所獲取的考慮風電出力相關性的常規機組有功出力方案，在和風電場有功出力的共同作用下，其總出力曲線可以很好地跟蹤負荷曲線，說明系統的有功出力可以滿足負荷以及網損需求，所得調度策略在滿足經濟最優的同時也滿足系統約束，策略具備一定實際參考價值.

5 結 論

針對涉及風電出力相關性的經濟調度分析忽略多維風電場出力相關性這一問題，通過建立基于MVTV Copula方法的多風電出力模型對電力系統經濟調度進行研究. 該經濟調度模型先對歷史數據采用K-means聚類分析，并利用MVTV Copula方法采樣生成隨機場景，將預測風電出力場景對應的常規機組運行成本和隨機場景對應的電力系統再調度費用最低做為調度目標，利用BSA進行經濟調度問題的求解. 為驗證所述方法的有效性，采用IEEE30節點系統，并結合我國某地3個相鄰風電場的歷史數據對所述方法進行仿真驗證，所得結果表明，根據MVTV Copula模型模擬獲得的風電數據所呈現的分布特性更貼合實測數據情況，并且計及相關性的再調度費用與實際再調度費用的更為接近，進一步說明多風電場相關性在電力系統研究中的重要性. 同時，調度人員可以根據所得隨機場景制定合理調度計劃，減小風電出力相關性對系統安全經濟運行的危害.