高速鐵路接觸網腕臂系統的力學特性

張 靜 ，劉金增 ，劉志剛 ，儲文平

（1. 西南交通大學機械工程學院，四川 成都 610031；2. 西南交通大學電氣工程學院，四川 成都 610031）

隨著高速鐵路的迅速發展，對高速鐵路接觸網安全運營的要求也越來越高. 弓網的動態性能決定了電能傳輸的可靠性和供電質量. 接觸網具有大跨度、高柔性的特點，對外部荷載的擾動非常敏感，在外部荷載（風載、覆冰、受電弓抬升力等）的作用下，接觸網會出現振動現象[1-7]. 過大的振動會導致弓網系統的受流性能惡化，更容易引起接觸網系統疲勞、受電弓離線等問題，嚴重時，甚至會發生刮弓事故.腕臂是接觸網的支撐裝置，對接觸網起支持和定位作用，并且承受電氣和機械載荷. 接觸線和承力索承受的環境載荷會傳遞到腕臂，容易引起腕臂的疲勞和破壞.

目前，國內外學者對腕臂做了大量研究，但這些研究主要集中在接觸網腕臂的檢測方面[8]，對腕臂的有限元分析計算不是很多，并且腕臂有限元計算都存在不同程度的簡化[9-12]. 文獻[10]腕臂結構的有限元模型采用梁單元BEAM188建立的，并編制了平腕臂的參數化分析程序，完成腕臂的模態分析. 文獻[11]采用BEAM188建立有限元模型，對腕臂進行靜力學和動力學分析，得到腕臂的最大應力和腕臂的模態以及諧響應分析，但銜接處的連接件（螺栓、定位環等）是一種簡化結構. 文獻[12]采用互推方法，給出一種腕臂系統應力傳遞的研究方法，并用試驗完成有限元模型的驗證. 但這些文獻的研究都忽略了螺栓以及套管雙耳等連接件對腕臂的影響，也都未考慮不同的環境荷載對腕臂應力水平的影響，使得腕臂系統分析計算結果不夠準確.

本文以高速鐵路接觸網正定位腕臂系統為研究對象，建立了一種新的腕臂有限元模型. 對腕臂不同環境荷載下的靜力分析，得到最大應力點分別在平腕臂和斜腕臂連接處的螺栓處和定位線夾處，此處為結構的薄弱點；通過對腕臂的動力學分析得到腕臂的固有頻率和振型，為腕臂設計和工作時避免共振提供依據；推導了載荷在腕臂系統中的傳遞規律和力傳遞到支柱的分布，為腕臂設計時的載荷合理分布提供參考依據. 最后，通過腕臂裝置的靜力學和動力學試驗結果和仿真結果的比較，驗證了腕臂結構有限元模型的正確性，完成了腕臂系統的力學特性研究.

1 腕臂靜力學分析

采用二次位移模式實體單元，建立腕臂的有限元模型如圖1所示. 有限元模型中考慮了套管雙耳和螺栓等連接件，為模擬定位線夾處的彈性約束，在定位線夾處施加彈簧約束. 在定位器與定位器支座連接處、定位管和斜腕臂連接處、平腕臂和上底座連接處以及斜腕臂與下底座連接處設置鉸接，如圖2所示，并在腕臂上下底座設置固定約束. 圖中：Lx、Ly、Lz分別為x、y、z軸的平移自由度；Rx、Ry、Rz分別為x、y、z軸的旋轉自由度.

接觸網采用“TM-120+CTM-150”全補償鏈形懸掛，跨距為50 m. 計算不同風速、不同覆冰厚度下腕臂的應力和變形分布. 根據接觸網網頁載覆冰負載和“之”分布的計算理論，得到腕臂不同工況下的荷載如表1所示. 將載荷和約束施加到腕臂有限元模型，得到腕臂在不同工況下的計算結果如圖3所示.

圖1 腕臂有限元模型Fig. 1 Finite element model of cantilever

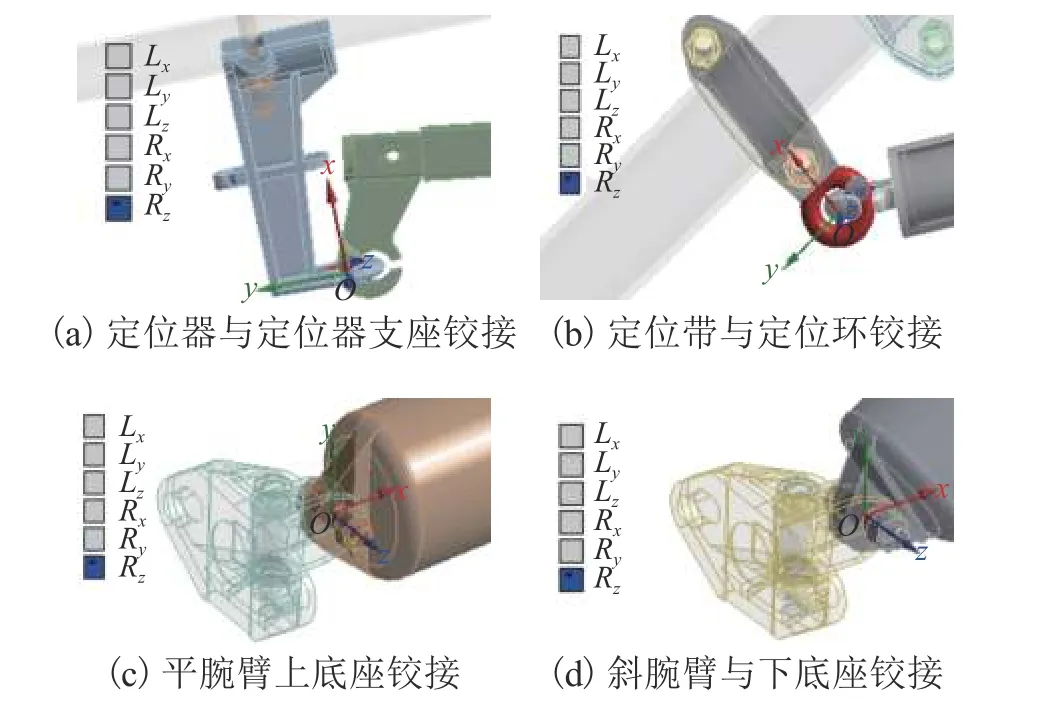
圖2 腕臂中的旋轉連接Fig. 2 Cantilever rotation connection

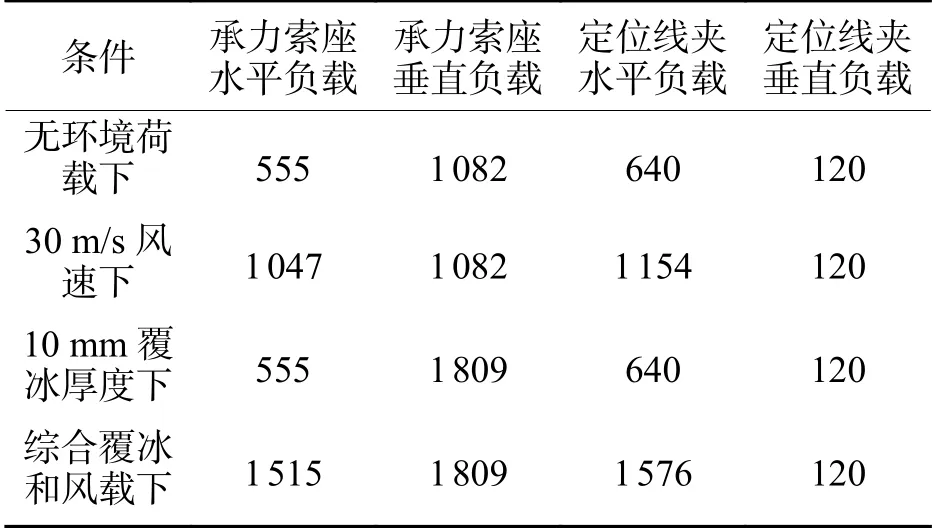
表 1 腕臂載荷Tab. 1 Cantilever load N

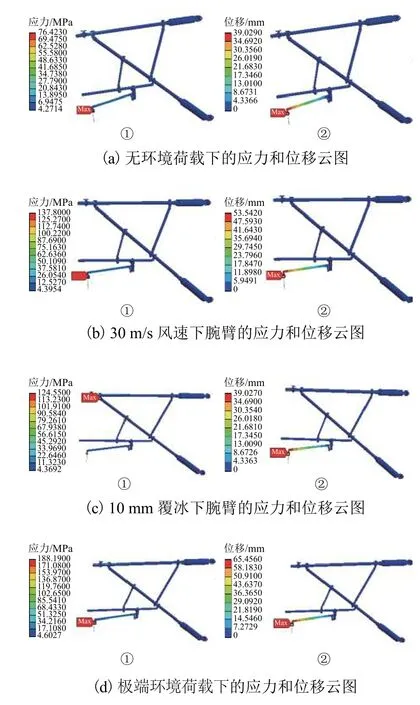
圖3 不同工況下腕臂的有限元計算結果Fig. 3 Finite element calculation value of cantilever with different working conditions

由圖3可知：在不同的環境荷載下，腕臂的最大應力點不同，覆冰載荷時最大應力點在斜腕臂和套管雙耳連接處的螺栓處，靜風荷載時最大應力點在定位線夾處. 在不同的環境荷載時，腕臂不同的受力點的荷載變化不同. 覆冰荷載主要以重力的形式作用到腕臂承力索座處，且為垂直向下的荷載，靜風載荷作用在承力索、接觸線和吊弦處，并通過承力索座和定位線夾傳遞到腕臂.

腕臂的最大位移均在定位線夾處，主要由于定位器能夠繞定位器支座旋轉，且定位線夾處的約束為彈簧約束，此處的位移為定位器繞定位器支座旋轉后的位移變形，包括定位器的彈性變形和剛體位移.

2 腕臂動力學分析

2.1 模態分析

采用ANSYS Workbench軟件，完成腕臂的整體模態分析，獲得模型的前10階固有頻率，計算結果如表2所示.

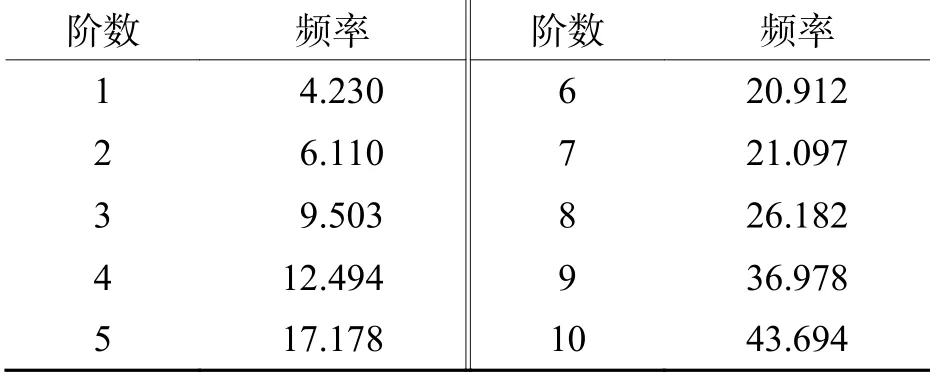
表 2 腕臂前10階固有頻率Tab. 2 First ten order natural frequencies of cantilever Hz

由表2可知：腕臂固有頻率從4.230 Hz不斷增加， 第1階振型的固有頻率最小，在低階振動時載荷的能量比較強，振動比較容易激發. 腕臂前6階振型如圖4所示.

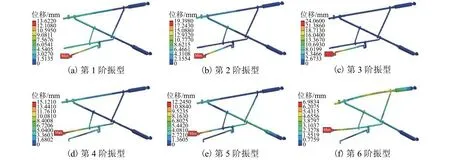
圖4 腕臂系統前6階模態振型Fig. 4 First six order vibration mode shape images of cantilever system

由圖4所示，腕臂系統在不同的階數時其振型不同：第1、2、3階振型下的腕臂在定位線夾處有較大的空間振動位移，第4、5、6階振型下的腕臂在定位管的端點處有較大的空間振動位移.

圖4所示的變形是腕臂模型各個節點之間的變形的相對量，顯示了各節點間的振動傳遞情況. 在振動中，腕臂各個桿件之間的夾角會發生變化，這將直接導致各個桿件的相位差發生改變，從而產生慣性力和慣性力矩，對腕臂工作的安全穩定性產生不良影響，導致各個桿件之間的相對位移發生變化，這將直接導致腕臂的結構會發生變化，同時，也會導致連接處的螺栓松動，這將對腕臂的安全可靠性帶來巨大的隱患.

2.2 載荷傳遞規律

考慮定位器和定位器支座之間的剛度、阻尼和摩擦等因素，建立了定位線夾通過定位器傳遞到定位器支座的響應模型，如圖5所示. 圖中：Fz為外部激勵載荷；Cj為關節處的阻尼；Kj為關節處的連接剛度；Ff為關節連接處的摩擦；Fq為外部激勵載荷傳遞到掛接另一側的載荷.

圖5 定位器鉸接模型Fig. 5 Articulation model of steady arm

研究載荷傳遞到腕臂底座的分布規律，建立力學模型可以對不同時速下腕臂的載荷傳遞規律進行研究.

由于鉸鏈非線性接觸特性中恢復力具有奇函數特性，故可對恢復力擬合兩組只包含奇次項的多項式，用一次項和三次項表示恢復力FRF的非線性函數，如式（1）.

式中：k1和k3分別為恢復力中一次項和三次項的剛度系數，恢復力中的剛度系數可有試驗數據擬合得到；xj為關節處的位移.

當定位器在受到外部振動時，由于定位器和定位器支座的工作狀態，其鉸鏈僅存在接觸一種狀態.鉸鏈在自由運動階段慣性力與外部激勵相平衡，在受拉階段除了鉸鏈的慣性力外，還受到黏性阻尼力、摩擦力和接觸力的作用. 因此，考慮阻尼、摩擦和非線性恢復力時，鉸鏈的非線性動力學方程為

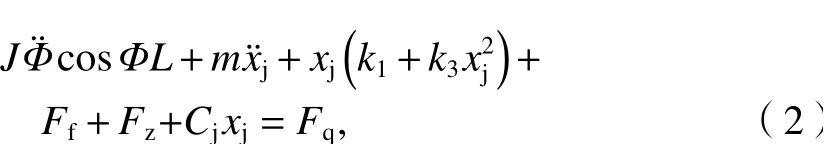
式中：J為定位器繞鉸鏈的轉動慣量；m為定位器質量；L為定位器的長度.

方程中考慮了定位器轉動、鉸接處的摩擦、阻尼和剛度對載荷傳遞的影響.

圖6為腕臂的桿件簡化模型，顯示了腕臂各個部分的長度和角度. 圖中：F為腕臂整體受到的外力.DE桿為腕臂支撐，僅受到軸力作用，將DE桿的軸力用F3和F4表示，腕臂的載荷F1～F8如圖7所示.

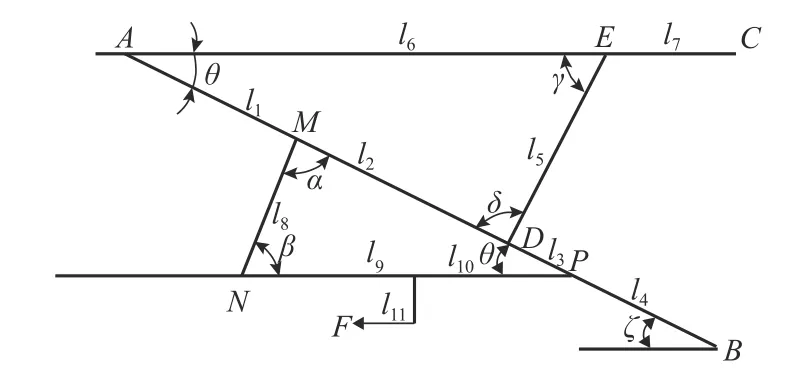
圖6 腕臂桿模型Fig. 6 Bar model of cantilever

圖7 腕臂載荷模型模型Fig. 7 Load model of cantilever

腕臂上框架ABC結構為超靜定結構，忽略桿DE的軸向變形，通過變形疊加，在F1、F2、F3的作用下DP段的變形方程如式（3）.

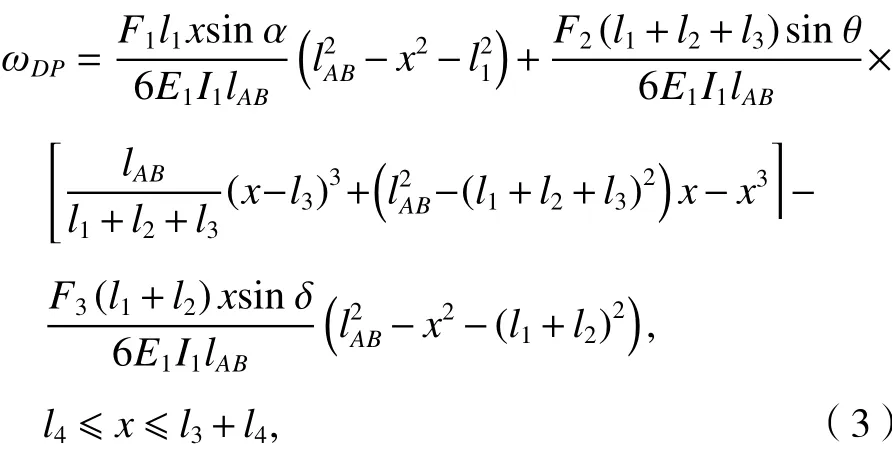
式中：E1為斜腕臂的彈性模量；I1為斜腕臂的慣性矩；lAB為斜腕臂AB的長度；ωDP為位移變形函數，后同.

式（3）可簡化為

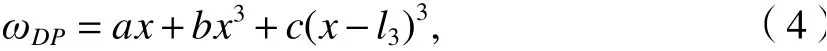
式中：

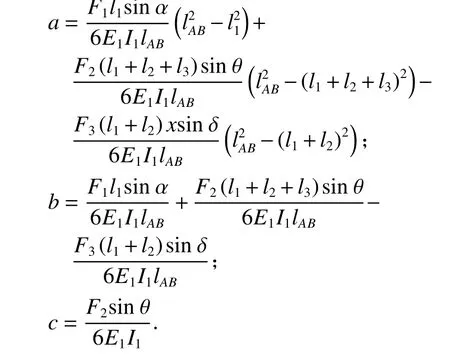
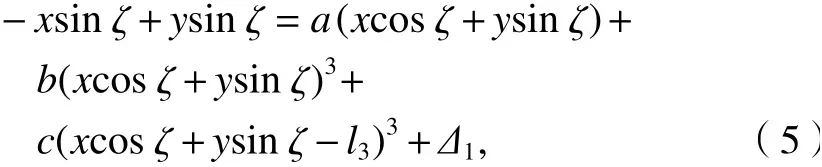
式中：Δ1為桿AC和桿AB的變形對桿AB影響的位移變形量.

同理桿AC的位移變形方程如式（6）所示.

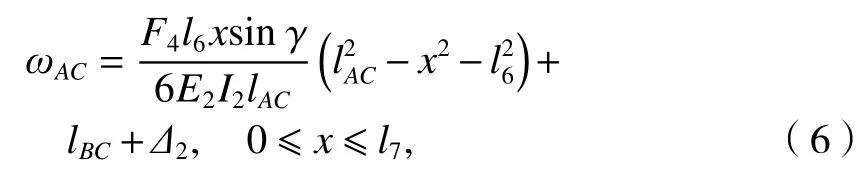
式中：E2為平腕臂的彈性模量；I2為平腕臂的慣性矩；lAC為平腕臂AC的長度；Δ2為桿AC的位移變形量.

通過聯立式（5）和（6），根據桿DE的長度不變的假設，可得到

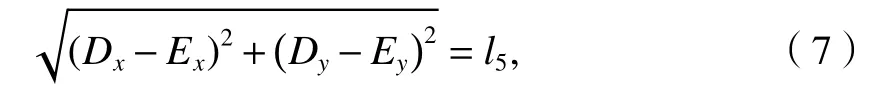
式中：Dx、Dy和Ex、Ey分別為點D和點E的x和y方向的位移.

解出F3、F4，從而框架結構ABC就可以以一個靜定結構得到F5～F8的值，得到定位器上的載荷傳遞到腕臂底座的規律.

本例中腕臂圓管的外徑為60 mm，內徑為50 mm，材料為不銹鋼，在定位器處施加式（8）的正弦形式水平載荷F，得到在正弦載荷下腕臂的響應.

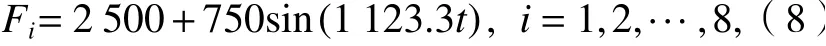
式中：t為時間.

本方法計算得到的F5～F8的值和有限元方法得到結果的對比如圖8所示.

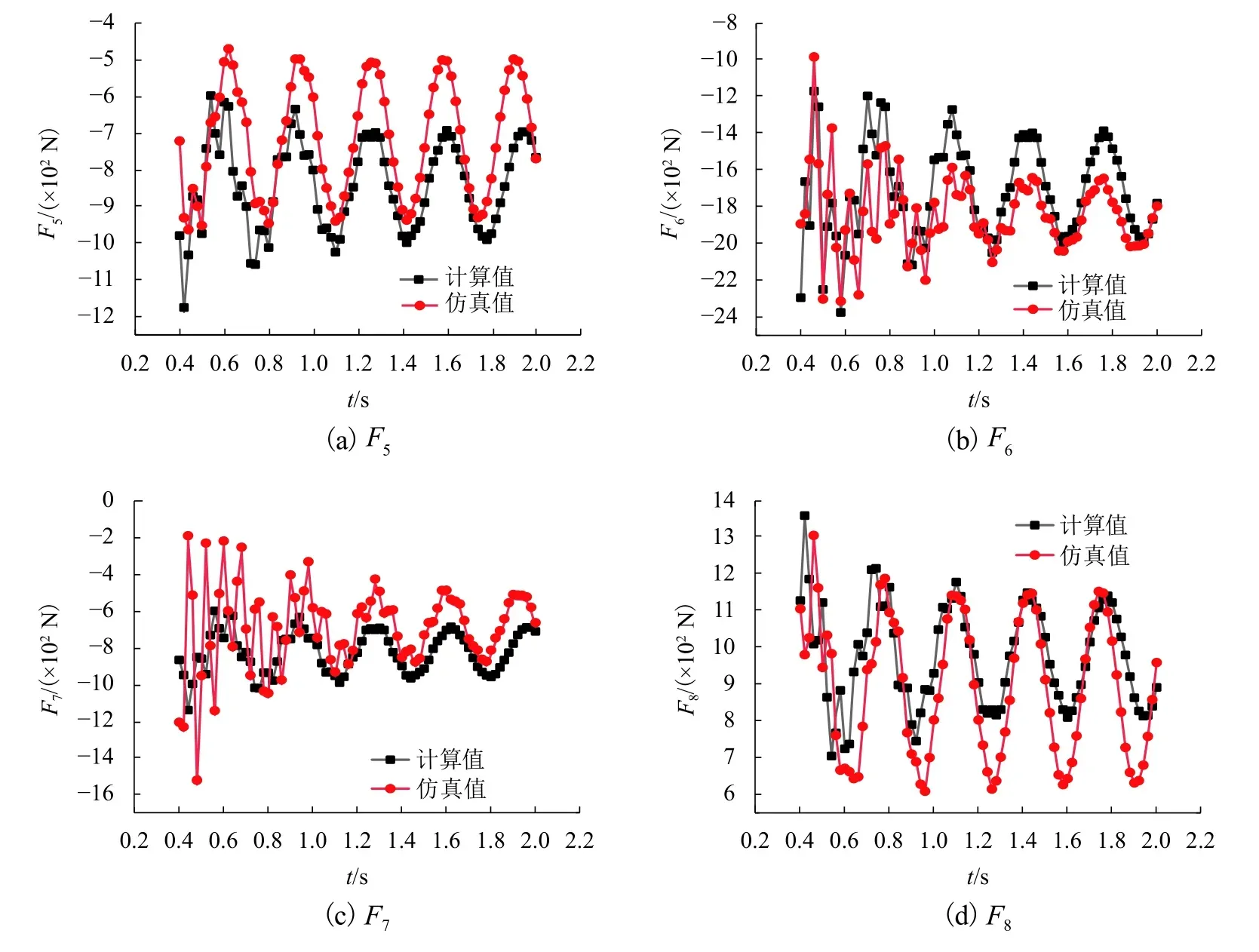
圖8 計算結果和仿真結果對比Fig. 8 Comparison between calculation value and simulation value

由圖8可知：仿真值的振幅大于計算值的振幅，主要原因是仿真數據中考慮了腕臂的摩擦、阻尼和接觸剛度等因素，但是計算式中并未完全考慮這些因素. 在曲線穩定后，計算值和仿真值的吻合性較好.

3 試驗驗證

腕臂系統試驗采用鋼腕臂，圖9（a）為腕臂試驗安裝圖，圖9（b）為腕臂的施加荷載圖. 試驗分為兩個部分，首先測試腕臂在靜態載荷下的靜態應變，通過疲勞試驗機對腕臂施加水平方向2.5 kN的靜態應力，然后施加動態荷載，測試腕臂在動態載荷下的動應變.

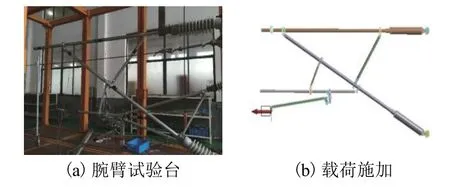
圖9 腕臂試驗Fig. 9 Cantilever test

在關鍵部位布置相應的應變片，采集試驗過程中靜態和動態應變數據，腕臂裝置采樣點分布和應變片如圖10所示.

采集靜態試驗結果并與有限元仿真結果對比，如表3所示. 由表3可知：測點 ①～⑦ 的測試值和計算仿真值的誤差在可接受的范圍內. 故可認為，在靜態時，腕臂的試驗結果和仿真結果一致.

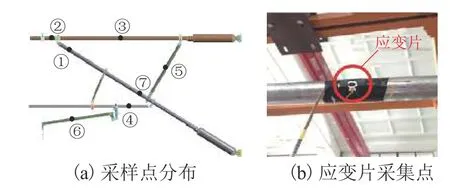
圖10 腕臂靜力學試驗Fig. 10 Cantilever statics experiment

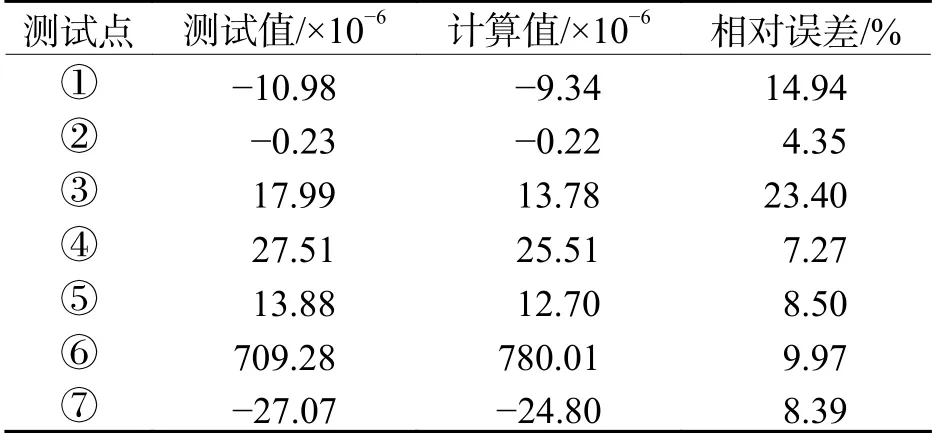
表3 腕臂裝置靜態強度試驗與仿真結果對比Tab. 3 Comparison of static strength test and simulation results of cantilever

動力學試驗采樣點布置和靜態試驗相同，通過疲勞試驗機對腕臂施加式（8）的載荷.

在腕臂結構振動平穩后采集動態應變數據，采集相同時段的數據，將仿真結果和試驗結果對比，結果如圖11所示.

圖11 測點 ①、③、④、⑦ 仿真和試驗結果對比Fig. 11 Comparison of simulation and test value of measuring points ①，③，④ and ⑦

由圖11可知，由于在仿真時未考慮套管雙耳等部件的滑動以及有可能發生的螺栓松動，在進行腕臂振動臺架試驗時，由于腕臂裝配以及其他因素的影響下，試驗時的振動較為劇烈，使得測試數據的幅值相較于仿真數據較大，但測試數據和仿真數據的平均值、趨勢以及振動頻率相同. 通過對腕臂結構靜態和動態的試驗和仿真結果的對比可以得出：腕臂結構仿真和試驗結果數據比較吻合，仿真結果是真實可信的.

4 結 論

1） 考慮螺栓、套管雙耳等連接件對腕臂的影響，建立了腕臂的實體有限元模型. 得到了腕臂在不同工況下的最大應力點和應力分布圖，為腕臂的優化設計提供思路.

2） 腕臂在振動時定位器的振動幅值較大，相比與其他部位振動劇烈，并結合靜態分析的結果，得到定位器處容易產生疲勞損傷.

3） 通過數值計算和仿真計算，載荷從定位點處傳遞到腕臂底座的傳遞路徑及其各桿件之間的載荷傳遞規律. 在腕臂優化設計時，為腕臂中載荷的合理分布提供依據.

4） 通過臺架試驗驗證了有限元模型的正確可靠性，同時也為其他型號腕臂的試驗提供參考依據.