基于混合高斯先驗分布的地質統計學反演

賀東陽，李海山，何 潤，王 偉

（中國石油勘探開發研究院西北分院，蘭州 730020）

0 引言

利用地表觀測的地球物理資料來推斷地下介質物理參數是一個地球物理反演問題。地震反演通過結合地震、測井、鉆井資料及已知的地質規律來估計儲層彈性參數，對巖性預測和流體識別具有重要的指導意義。常規的確定性反演只能提供一個最優解［1-3］，無法對模型參數進行不確定性分析。而概率統計反演方法將反演結果以概率的形式表示，可以獲得模型參數的多次實現，能夠對反演結果進行不確定性分析。因此，概率統計反演在一定程度上可以避免反演結果不確定性導致的預測風險。概率統計反演分為貝葉斯反演和地質統計學反演兩類方法。

在貝葉斯反演中，將模型參數的解表示為后驗概論密度函數［4-6］。后驗概率密度函數的解析解通常無法求取，可利用馬爾科夫蒙特卡洛（Markov chain Monte Carlo，McMC）方法進行抽樣求解［7-8］。張廣智等［9］將該算法應用于疊前地震反演，獲得了縱橫波阻抗和密度反射系數。王輝等［10］利用該算法在疊前域反演了縱橫波速度和密度。但對于高斯線性假設，即模型參數的先驗概率密度函數是高斯分布并且正演算子可以線性化，則可以獲得后驗概率密度函數的解析解［5］。Buland 等［11］通過線性高斯假設并利用疊前地震資料進行縱橫波速度和密度參數反演。滕龍等［12］通過線性高斯假設進行彈性參數與物性參數的聯合反演。為表征離散巖性和流體對模型參數的分布影響，Grana 等［13-14］將模型參數的先驗分布表示為混合高斯分布，通過線性假設得到混合高斯線性反演解。

在地質統計學反演中，通過序貫模擬或非序貫模擬算法來構建模型參數的先驗信息，然后不斷擾動模型參數來匹配觀測數據，從而得到模型參數反演解，這種方法通常計算量非常大，且不能保證反演解收斂。Bortoli 等［15］和Haas 等［16］最早將序貫高斯模擬算法應用于地質統計學反演。余振等［17］利用序貫高斯模擬和序貫指示模擬算法進行地質統計學反演，并實現了高分辨率的流體預測。由于序貫高斯模擬通常須要對模型參數進行正態變換，Soares 等［18］、Caetano 等［19］、Azevedo 等［20］利用直接序貫模擬算法進行地震隨機反演。為快速構建模型參數的先驗信息，孫瑞瑩等［21］、王保麗等［22］、Yang等［23］利用非序貫模擬的FFT-MA 譜模擬算法進行隨機反演。針對兩點地質統計學的不足，González等［24］和劉興業等［25］利用多點地質統計學進行地震隨機反演。由于傳統的序貫模擬算法通過求解克里金方程組來獲得待模擬點的均值和方差［26-29］，再利用蒙特卡洛的方法逐點隨機模擬該點的值。當克里金方程組較大時，求解過程非常耗時。因此，Hansen 等［30］將線性高斯理論與序貫模擬相結合來求取待模擬點的后驗均值和方差，避免求解大型協方差矩陣和擾動優化過程，直接獲得模型參數的多次實現，但是該方法沒有考慮離散巖性和流體對模型參數的先驗分布影響，只能單一地反演連續變量的模型參數。

在Hansen 等［30］的研究基礎上，將模型參數的先驗分布表示為受離散巖性影響的混合高斯分布，并將線性混合高斯理論與序貫模擬相結合，同時獲得聲波阻抗與巖性的多次實現，以期反演結果具有較好的空間連續性和穩定性。

1 序貫模擬的線性混合高斯反演

1.1 混合高斯先驗分布

由于離散巖性的影響，模型參數如彈性阻抗、孔隙度、含水飽和度等連續變量呈現多峰的混合高斯分布。模型參數服從多峰的混合高斯概率密度函數，可以表示為

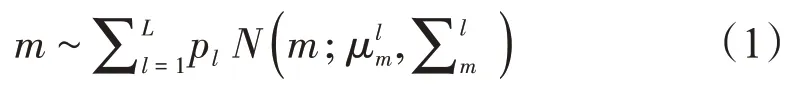
式中：L為高斯分量的個數，這里表示離散巖性的個數；pl為第l個高斯分量的先驗權值；N為混合高斯的第l個高斯分量，表示為

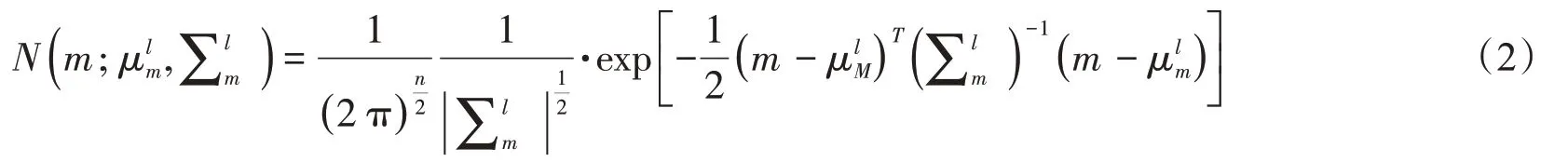
1.2 混合高斯線性反演解

假設觀測數據d和模型參數m之間的正演關系可以用線性算子G表示，即d=G m+ε，地震噪聲ε服從高斯分布。如果模型參數m的先驗信息服從混合高斯分布，那么模型參數m的后驗條件分布也服從混合高斯分布［13-14］，如下：

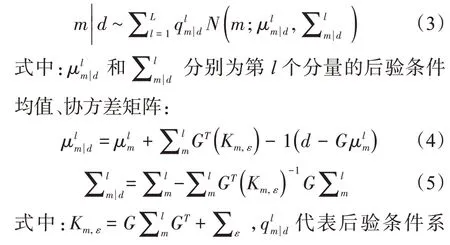
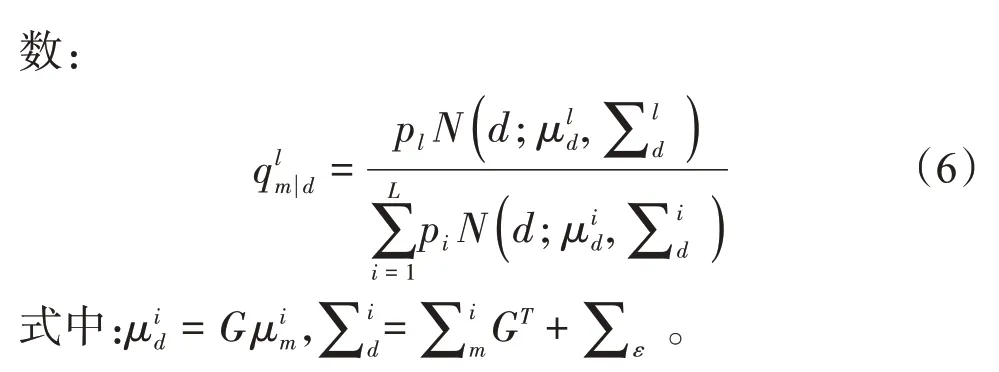
1.3 線性混合高斯序貫采樣

為了提高反演解的精度和穩定性，將低頻模型df作為待采樣點的條件數據，低頻模型可以通過井插值或者其他方法獲取。低頻模型可以表示為［31］：

式中：εf是一個協方差為∑f的噪聲，描述了反演結果與模型參數的相似度。

將d=G m+ε和式（7）聯合可以寫成：

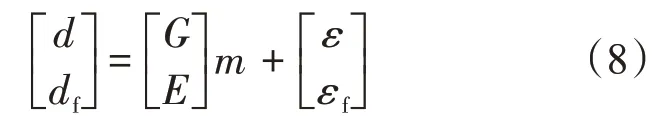
式中：E表示單位矩陣。

如果d′=，則式（8）可以寫成：

根據Hansen 等［30］提出的線性高斯序貫采樣理論，在線性混合高斯序貫采樣過程中，須要估算待采樣點mx在三類條件數據（mk，d及df）下的后驗條件分布，這里的mk表示已采樣點的模型參數自身。該后驗條件分布mx|(mkd,df), 也服從混合高斯分布，即mx|(mk,d′) 服從混合高斯分布：

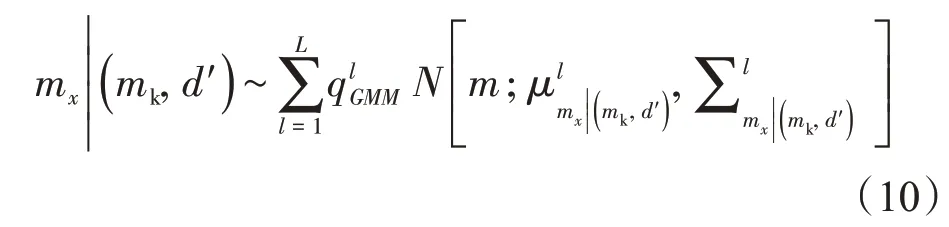
其均值和協方差分別變為：

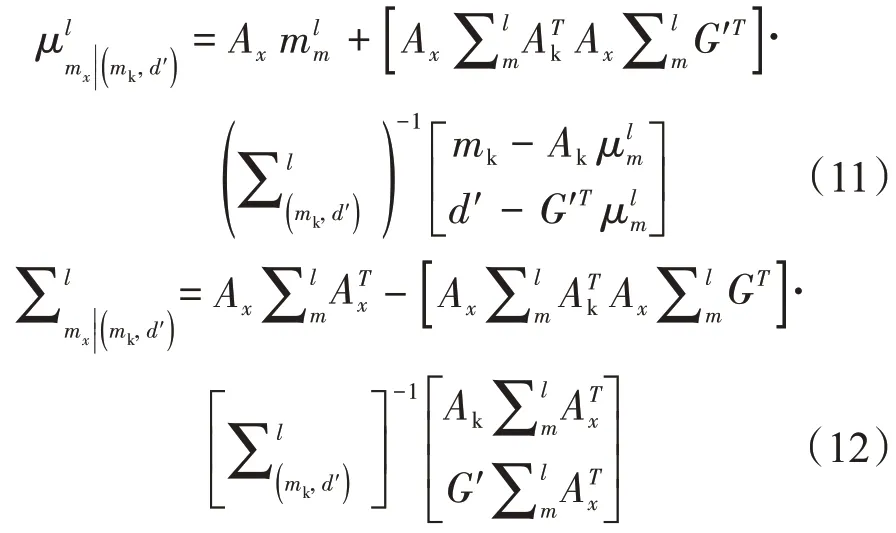
后驗條件權值變為：

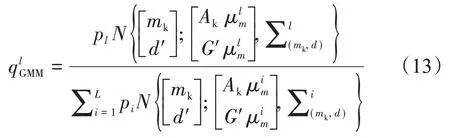
線性混合高斯序貫采樣的步驟如下：

（1）定義模擬網格，利用隨機種子隨機訪問模擬網格中的待采樣點mx。

（2）利用式（11）—（13）分別計算待采樣點的后驗條件均值、協方差以及后驗條件權值

（3）比較后驗條件權值系數確定待采樣點的離散巖性，即高斯分量，然后從確定的高斯分量中隨機抽取一個值，作為當前待采樣點的連續變量的模型參數值。

（4）隨機訪問下一個待采樣點，并將上一次采樣點的值作為該點的條件數據。

（5）重復步驟（1）—（4），直到訪問完所有采樣點。

這種逐點序貫采樣的方法，在反演每一個點的時候，由于考慮了模型參數、觀測數據及低頻模型等多類條件數據，實際上是對空間相關的后驗分布進行采樣，使得反演結果具有較好的空間連續性。通過選取合理的反演時窗和模擬鄰域，可以避免大型協方差矩陣的計算，從而提高計算效率。

2 模型測試

為驗證本文提出的方法的有效性，這里利用二維模型來驗證本文提出方法的有效性。

圖1（a）是聲波阻抗模型，圖1（b）是巖相模型，圖1（c）是真實記錄，一共206 道，每道302 個采樣點，并假設每個網格大小為1 m×1 m。模型中的黑線表示抽取的偽井，偽井可以用來求取協方差矩陣，并在反演過程中充當條件數據。圖2 是從抽取的偽井中統計的變差函數，利用球狀理論變差函數來擬合實驗變差函數，聲波阻抗在橫向上的變程為110 m，縱向上的變程為75 m。利用變差函數與協方差函數的關系：γ（h）=1-C（h），可以求取聲波阻抗的空間協方差。首先進行無噪測試，反演結果如圖3 所示。可以看到，反演的兩次聲波阻抗、巖性及合成記錄與模型數據吻合較好。其中2 次巖性反演結果的歸類正確率分別為93.63%和93.53%。圖3（g）和圖3（h）是2 次反演的砂巖概率，可以用于巖性的不確定性分析，然后進行信噪比為4 的加噪測試，反演結果如圖4 所示。可以看到，2 次的反演結果與合成記錄的精度較圖3 有所下降，但仍然與模型數據能夠較好地吻合。其中，2 次巖性反演結果的歸類正確率分別為92.18%和92.24%。圖4中砂巖概率的2 次反演結果較圖3 的結果出現了一定的波動性，這是加入的噪聲所引起的，但這并沒有對巖性的歸類結果產生大的影響。

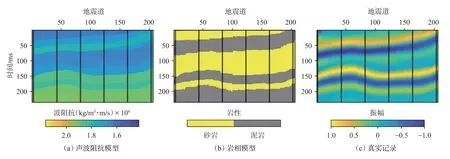
圖1 模型數據Fig.1 Model data

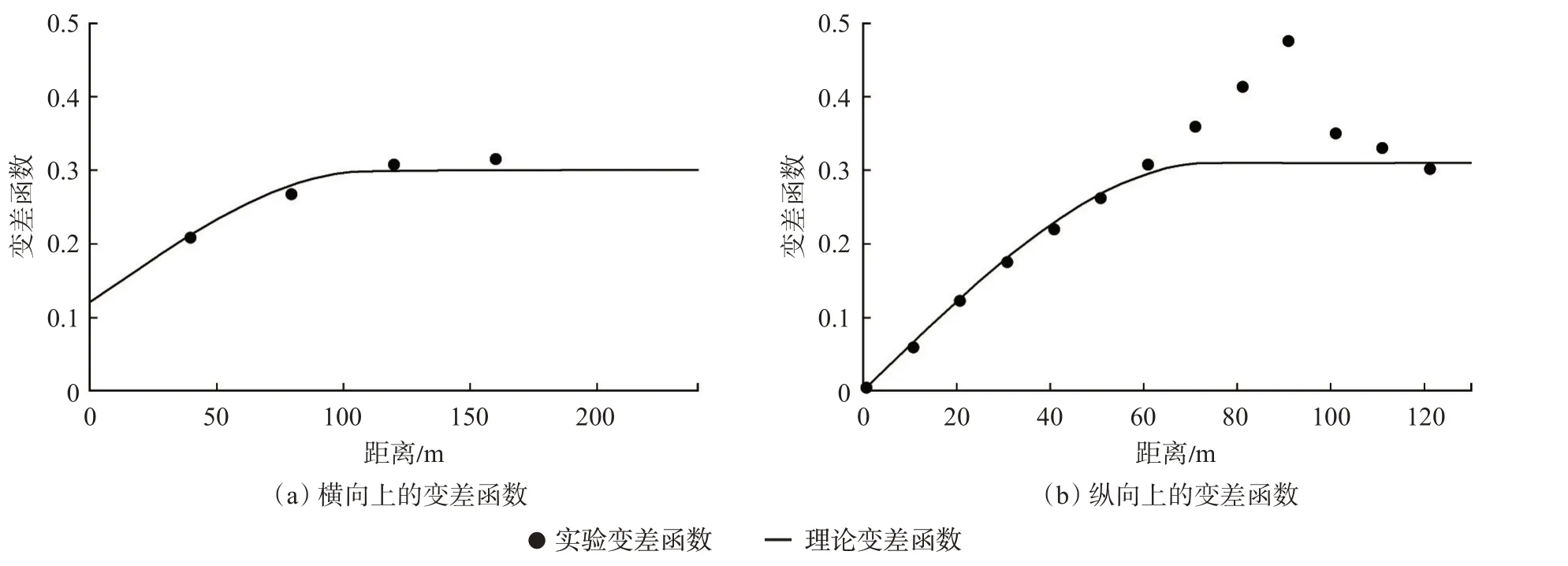
圖2 聲波阻抗的變差函數統計Fig.2 Variogram statistics of acoustic impedance

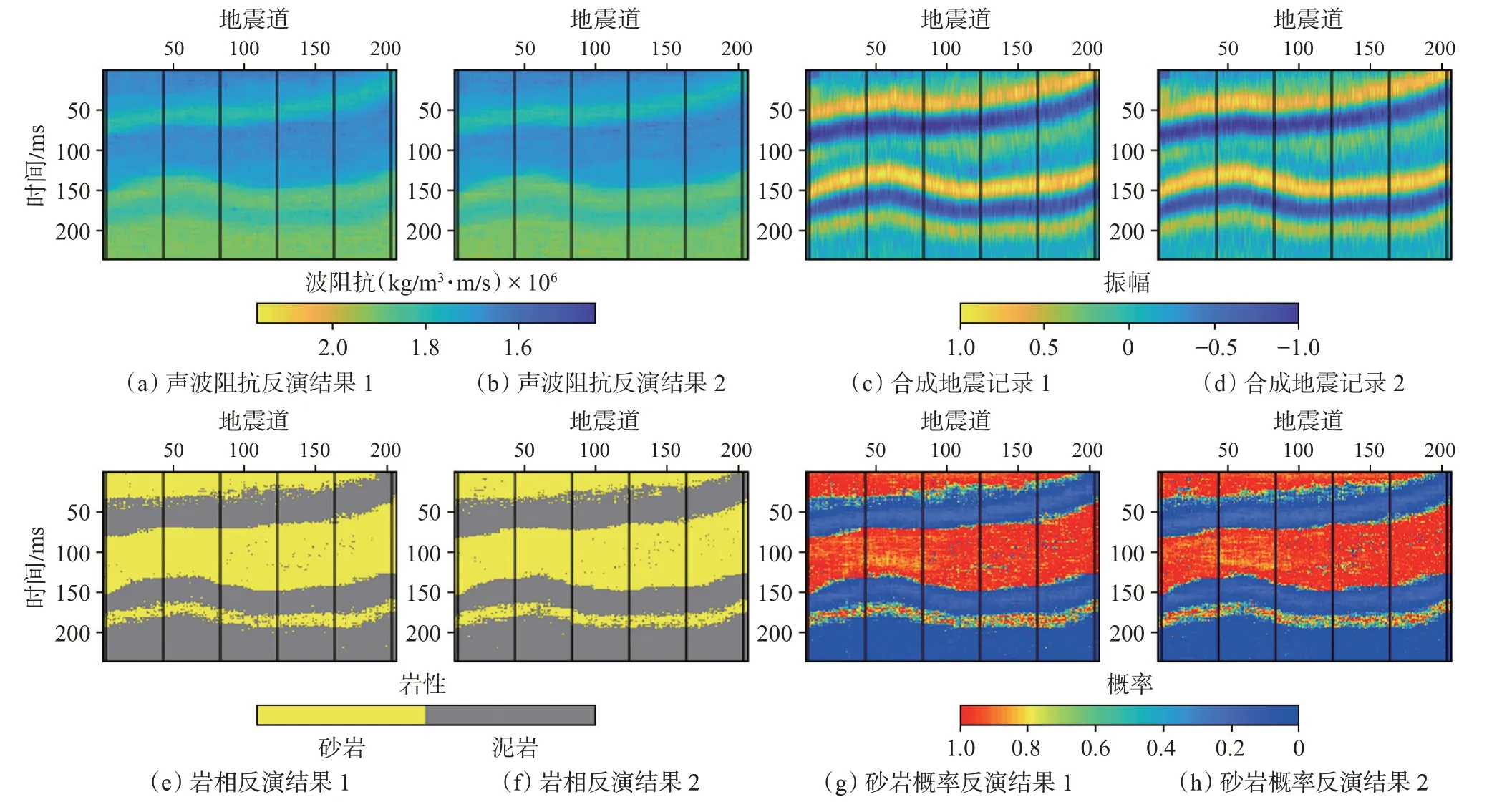
圖3 無噪聲時的兩次反演結果Fig.3 Two inversion results without noise

圖4 信噪比為4 時的兩次反演結果Fig.4 Two inversion results when SNR is 4

3 實際應用

為了驗證該方法的實際效果，以國內東部某油田的工區資料進行了應用。該工區以砂泥巖為主，且砂巖的阻抗較高，泥巖的阻抗較低。圖5（a）為原始的二維疊后地震記錄，共有139 道，反演時窗為2 450～2 680 ms，采樣率為2 ms，其中A 井用作驗證井。圖5（b）和圖5（c）分別是聲波阻抗和巖性的反演結果，可看到反演結果具有較好的橫向展布，將反演的聲波阻抗與子波合成的地震記錄如圖5（d）所示，與真實的地震記錄吻合較好。圖5（e）是砂巖概率的反演結果，可以預測有利儲層的位置。為了驗證本文提出的方法的可靠性，將A 井位置處抽取的反演結果和A 井數據對比，如圖6 所示，可以看到聲波阻抗吻合較好，巖性結果除了少數點被錯誤歸類外，大部分與真實巖性吻合較好，歸類正確率達82.76%。

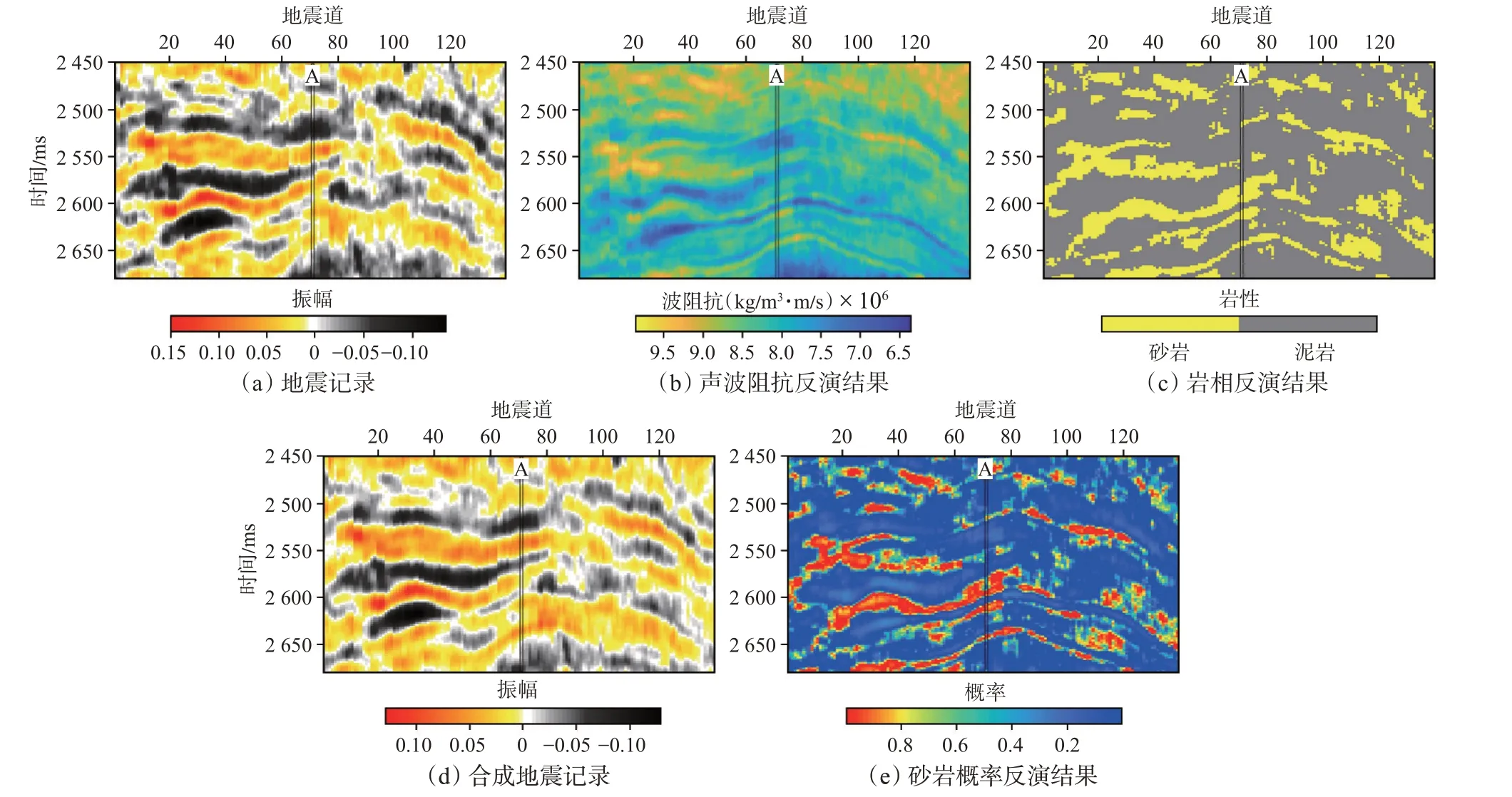
圖5 地震記錄和反演結果Fig.5 Real seismogram and inversion results

4 結論

（1）混合高斯模型能夠表征模型參數的多峰分布，將其與地質統計學的序貫模擬相結合可以同時反演連續變量和離散巖性。相比傳統的地質統計學反演，這種方法在序貫采樣的過程中，同時考慮了模型參數自身、觀測數據及低頻模型，屬于邊模擬邊反演的過程，而不是先模擬再反演的過程。

（2）低頻模型的加入能讓反演結果更加穩定，不易受噪聲的影響，空間相關的后驗序貫采樣使得反演結果具有較好地空間連續性。這種方法還可以用于彈性阻抗反演、疊前AVO 反演。

（3）需要指出的是，這種邊模擬邊反演的方法由于直接以地震數據作為條件數據，缺少了模型參數的小尺度變化性，使得這種方法的垂向分辨率受到一定的影響。