中學(xué)生物理成績與其它多門學(xué)科的相關(guān)性研究

摘 要：中學(xué)階段在人的求學(xué)一生中具有承上啟下的重要作用，而物理學(xué)科具有重要的基礎(chǔ)地位.所以有必要專門研究中學(xué)生物理學(xué)習(xí)成績與其它多門功課之間的相關(guān)性問題.通過對中學(xué)生各個學(xué)科的成績進行對比，采用SPSS23軟件處理數(shù)據(jù)得到偏相關(guān)系數(shù)，定量得出物理與數(shù)學(xué)、化學(xué)相關(guān)程度較高，與語文關(guān)聯(lián)程度很低，與英語、生物相關(guān)程度相對中等的結(jié)論.

關(guān)鍵詞：中學(xué)生;物理成績;相關(guān)性;偏相關(guān)系數(shù);學(xué)習(xí)遷移

中圖分類號：G633.7 文獻標(biāo)識碼：B 文章編號：1008-4134（2021）01-0007-04

作者簡介：朱俊林（1988-），男，安徽阜南人，碩士，助教，研究方向：大學(xué)物理教學(xué)及物理教育研究.

1 問題的提出

知識原本并無學(xué)科之分，隨著生產(chǎn)力的發(fā)展和人類文明的進步，分工越發(fā)的精細.而知識的分類也越來越規(guī)范，由此誕生了學(xué)科.中學(xué)在人的求學(xué)一生中具有承上啟下的重要作用，同時物理學(xué)科具有重要的基礎(chǔ)地位.學(xué)習(xí)物理能夠啟發(fā)學(xué)生探索自然好奇心，同時也能為學(xué)生今后的深造打下基礎(chǔ).所以我們有必要專門研究影響中學(xué)生物理學(xué)習(xí)成績的諸多因素.不可否認個體的認知差異以及生活經(jīng)歷對學(xué)習(xí)物理有著重要的影響，本文著重探索的是中學(xué)生物理成績與其它諸多門功課之間的規(guī)律.

作為教師經(jīng)常能聽到一些說法，能學(xué)好數(shù)學(xué)的學(xué)生也能學(xué)好物理，能學(xué)好物理的學(xué)生腦瓜聰明等類似的話.這是教師的日常教育經(jīng)驗，屬于教育認識的習(xí)俗形式.教育習(xí)俗性認識及由此產(chǎn)生的日常教育經(jīng)驗通常會有局限性，浮于表面.能不能經(jīng)得起考驗，必須用科學(xué)的方法來檢驗.

2 已有研究綜述

現(xiàn)成的許多類似研究，大多是某兩門功課之間的對比.例如，高中生數(shù)學(xué)對物理成績影響的量化研究[1]，中學(xué)階段各學(xué)科相關(guān)系數(shù)差異分析及教學(xué)建議[2]等.大多數(shù)的研究者做相關(guān)性分析時，樣本采集幾乎都是割裂出要分析的兩組數(shù)據(jù)做皮爾遜相關(guān)系數(shù)計算.

相關(guān)系數(shù)常用來反映變量之間的密切程度，問題是如果把其它的科目全都忽略而單獨拿兩門功課來研究它們之間的關(guān)系，得出的結(jié)論很可能是片面的.因為中學(xué)生要學(xué)的功課不止一門，在校期間學(xué)習(xí)時間總量是一定的，如果是單獨用兩個學(xué)科成績做相關(guān)性比較的話，忽略了其它學(xué)科的影響也是不科學(xué)的.

基于以上考慮，除了把單獨的兩組變量列出做出一般性的散點圖外，本文特別考慮到了高中理科所有的高考科目.列出六組變量運用控制變量法得出偏相關(guān)系數(shù)，因為充分考慮到了多變量影響，所以得出的結(jié)論更有說服力.

3 研究設(shè)計

3.1 研究目的及意義

本文選取某中部省份一所重點中學(xué)兩千多名學(xué)生的六大學(xué)科成績數(shù)據(jù)，旨在通過數(shù)據(jù)挖掘，量化分析高中生物理成績與語文、數(shù)學(xué)、英語、化學(xué)、生物五大高考科目之間的相關(guān)性.

《國家中長期教育改革和發(fā)展規(guī)劃綱要（2010-2020年）》指出全面提高普通高中學(xué)生綜合素質(zhì)，高中生要學(xué)習(xí)的文化科目中，語、數(shù)、英、物、化、生六科占據(jù)著極重要地位.通過本研究讓更多的人認識不同學(xué)科之間的相關(guān)性和它們的特點，促進學(xué)生各學(xué)科的全面提高，提升高中生的綜合素質(zhì).

同時也讓更多的人認識學(xué)習(xí)遷移理論，服務(wù)于一線教師，把遷移理論用于學(xué)生培養(yǎng)，對于高中生的全面均衡發(fā)展具有重要意義.

3.2 樣本選取

除去缺考人員設(shè)定三個樣本：設(shè)定樣本一，高一718人;樣本二，高二709人;樣本三，高三664人.樣本選自不同的群體，不同學(xué)段，因此具有廣泛的代表性.

3.3 數(shù)據(jù)處理工具

本次研究涉及一萬兩千多個數(shù)據(jù)處理，有六組變量而且數(shù)據(jù)之間可能存在復(fù)雜關(guān)系.因此借助SPSS Statistics23軟件，利用了散點圖功能和相關(guān)性分析功能.

3.4 研究方法及分析角度

首先，把不同樣本的物理成績與語文、數(shù)學(xué)、英語、化學(xué)、生物成績單獨列出來得到散點圖，觀察分布尋求規(guī)律.

其次，分別把樣本一、樣本二、樣本三做偏相關(guān)性分析.偏相關(guān)性是指當(dāng)兩個變量同時與第三個變量相關(guān)時，將第三個變量的影響剔除.在實際情況中，相關(guān)分析往往有第三變量的影響，而使得相關(guān)系數(shù)不能真實地體現(xiàn)其線性相關(guān)程度.所以必須要用控制變量法，得出的結(jié)論才是更客觀的.不考慮到這一點的話，難免會得出片面的結(jié)論.

最后，對相關(guān)性的量化指標(biāo)做一個綜合的對比得出結(jié)論.

4 研究結(jié)果與分析

4.1 物理與語文成績的相關(guān)性分析

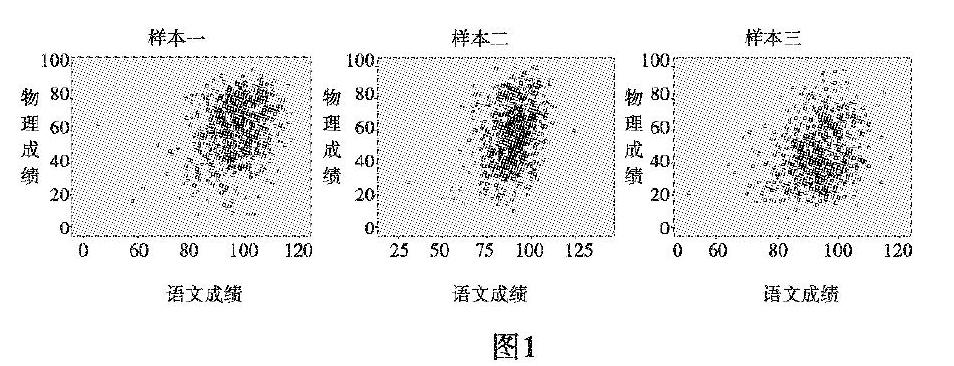
如圖1分別是樣本一、二、三物理成績與語文成績的散點分布圖.即使是從高一到高三不同學(xué)段、不同群體，定性地看物理成績與語文成績正相關(guān)性不明顯.

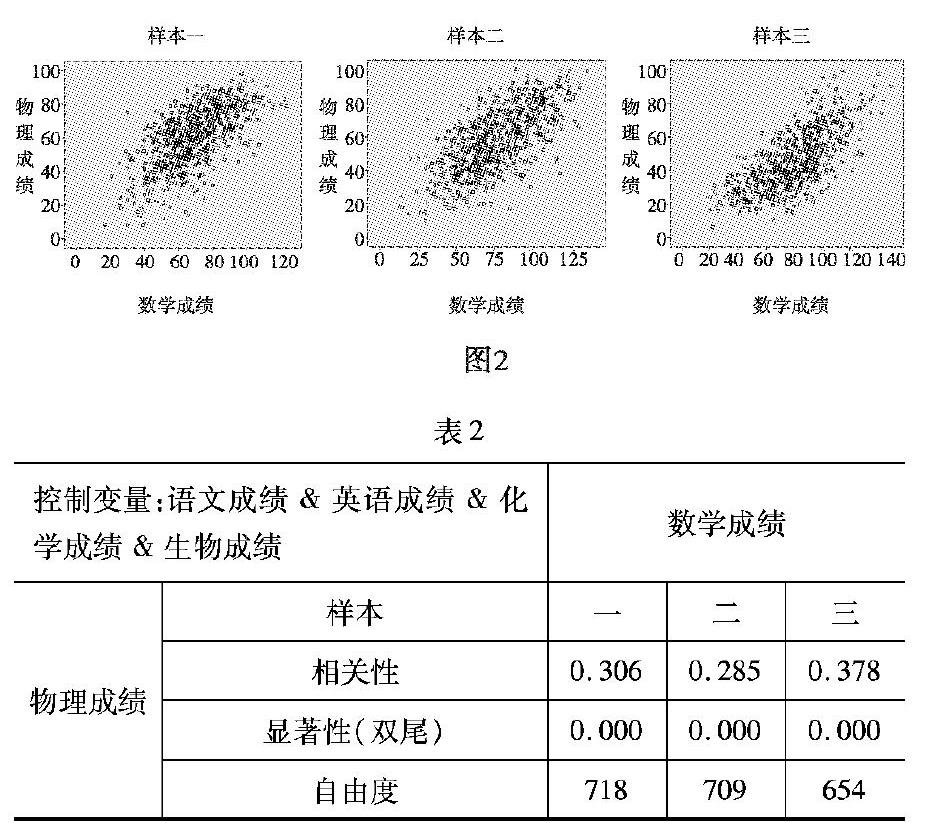
下面做進一步分析，對三個樣本分別做偏相關(guān)性分析.由表1可見，樣本一相關(guān)性0.051小于顯著性（雙尾）0.172，樣本二0.027小于顯著性（雙尾）0.465，樣本三相關(guān)性0.008明顯處于低水平.由此得出結(jié)論：中學(xué)生的物理成績與語文成績相關(guān)性很小處于低水平.

4.2 物理與數(shù)學(xué)成績的相關(guān)性分析

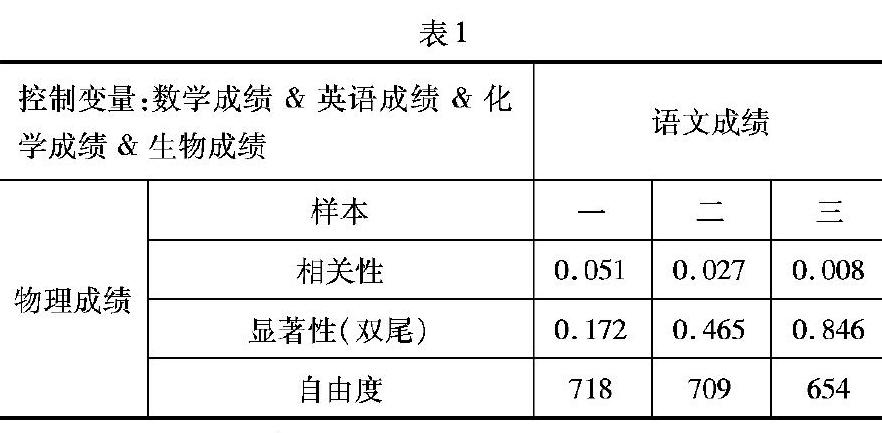
如圖2分別是樣本一、二、三物理成績與數(shù)學(xué)成績的散點分布圖，呈現(xiàn)出明顯的正相關(guān)性.

進一步分析由表2可見，樣本一相關(guān)性0.306大于顯著性（雙尾）0.000，樣本二0.289大于顯著性（雙尾）0.000，樣本三相關(guān)性0.378大于顯著性（雙尾）0.000.由此得出結(jié)論：中學(xué)生物理成績與數(shù)學(xué)成績相關(guān)性明顯而且處于較高水平.

4.3 物理與英語成績的相關(guān)性分析

如圖3分別是樣本一、二、三物理成績與英語成績的散點分布圖.與語文相比類似相關(guān)性不明顯.

進一步分析由表3可見，樣本一相關(guān)性0.170大于顯著性（雙尾）0.000，樣本二0.098大于顯著性（雙尾）0.009，樣本三相關(guān)性0.023小于顯著性（雙尾）0.555.我們發(fā)現(xiàn)物理與英語的相關(guān)性比較復(fù)雜，其相關(guān)性比語文高比數(shù)學(xué)小，相對處于中等水平.

4.4 物理與化學(xué)成績的相關(guān)性分析

如圖4分別是樣本一、二、三物理成績與化學(xué)成績的散點分布圖，呈現(xiàn)出明顯的正相關(guān)性.

進一步分析由表4可見，樣本一相關(guān)性0.361大于顯著性（雙尾）0.000，樣本二0.386大于顯著性（雙尾）0.000，樣本三相關(guān)性0.316大于顯著性（雙尾）0.000.由此得出結(jié)論：中學(xué)生物理成績與化學(xué)成績相關(guān)性明顯而且處于較高水平.

4.5 物理與生物成績的相關(guān)性分析

如圖5分別是樣本一、二、三物理成績與生物成績的散點分布圖.與生物相比呈現(xiàn)出正相關(guān)性，相關(guān)性沒有數(shù)學(xué)、化學(xué)明顯卻又比語文、英語明顯.

進一步定量分析，由表5可見，樣本一相關(guān)性0.226大于顯著性（雙尾）0.000，樣本二0.185大于顯著性（雙尾）0.000，樣本三相關(guān)性0.220大于顯著性（雙尾）0.000.由此得出結(jié)論：中學(xué)生物理成績與生物成績相關(guān)性處于較高水平.

4.6 結(jié)論

通過對比分析，物理與其它五門學(xué)科的相關(guān)性P物數(shù)>P物化>P物生>P物英>P物語.同時也能明顯地看出物理與數(shù)學(xué)、化學(xué)的相關(guān)性處于相對較高的位置，物理與語文處于一個相對偏低的位置.

如何理解這種現(xiàn)象呢，從學(xué)科內(nèi)容上來看，高中數(shù)學(xué)需要學(xué)生具備分析計算能力、邏輯推理能力和空間想象能力等.高中化學(xué)需要學(xué)生具備必要的計算能力和很強的邏輯推理能力.而高中物理也是需要很強的計算能力和空間想象能力，邏輯推理能力尤為重要.學(xué)習(xí)遷移是指人在一種情境中的學(xué)習(xí)影響他在其它情境中的學(xué)習(xí).桑代克的共同要素認為，學(xué)習(xí)遷移就是相同聯(lián)結(jié)的遷移，在兩種學(xué)習(xí)中存在著共同的聯(lián)結(jié)，一種學(xué)習(xí)上的進步轉(zhuǎn)移到另一種學(xué)習(xí)上去.物理與數(shù)學(xué)、化學(xué)的正遷移效果明顯.

語文、英語是語言類學(xué)科，在內(nèi)容上它們和理科的物理差異性很大.但語言類學(xué)科的學(xué)習(xí)對記、用、模仿的相關(guān)能力要求很高.雖然它們與物理的相關(guān)性不那么明顯，但是也存在一定的相關(guān)性.形式訓(xùn)練說認為，學(xué)習(xí)的遷移就是非物質(zhì)的心靈功能受到發(fā)展的結(jié)果.即通過某種學(xué)習(xí)，使某種心靈功能得到訓(xùn)練，從而轉(zhuǎn)移到其它學(xué)習(xí)上去.以這種觀點來看，也能解釋物理與語文、英語的某種相關(guān)性，只是在此處不占主導(dǎo)作用.

生物是一個文理摻半的學(xué)科，一方面對學(xué)生的邏輯推理、計算能力有一定要求，另一方面有眾多需要記的概念和名詞.它與物理的相關(guān)性綜合了數(shù)學(xué)和語文與物理的相關(guān)性.這樣就不難理解相關(guān)性P物數(shù)>P物化>P物生>P物英>P物語這樣的現(xiàn)象了.

5 結(jié)束語

就物理與其它五門學(xué)科的相關(guān)性P物數(shù)>P物化>P物生>P物英>P物語結(jié)論和它們量化的指標(biāo)而言，本文雖然是以考試分數(shù)為載體來進行研究，但也應(yīng)客觀地認識到，考試分數(shù)受多方面影響，僅僅依靠收集、整理、統(tǒng)計的一些數(shù)據(jù)還是不能夠完全反映中學(xué)生的學(xué)習(xí)能力的.教育的天職是促進個體的發(fā)展，不能唯分數(shù)論.馬克思主義教育學(xué)指出：既要看到教育現(xiàn)象的復(fù)雜性，不能用簡單化的態(tài)度和方法來對待教育研究，又要堅信教育現(xiàn)象是有規(guī)律可循的.

本研究充分考慮到教育影響，教育影響即教育活動中教育者作用于學(xué)習(xí)者的全部信息.學(xué)生某一科的學(xué)習(xí)偏好很容易受科任教師的影響.例如，如果某個富有感染力的教師深受學(xué)生喜歡，課堂效果極好，學(xué)生平時也偏愛在這一科多花一些時間，樣本數(shù)據(jù)過少和方法不當(dāng)?shù)脑捄苋菀椎贸銎畹慕Y(jié)論.因此選取兩千多個學(xué)生跨度不同、學(xué)段不同群體的上萬個數(shù)據(jù)，應(yīng)用到了控制變量法，從而有效避免了可能的偏差.例如，研究物理與語文相關(guān)性時用偏相關(guān)性顯著性雙尾是0.846，與不用控制變量法得到的結(jié)論有明顯的不同.

一線教師如果能充分認識到不同學(xué)科的相關(guān)性以及背后的理論體系，就可以通過表層的現(xiàn)象分析出

背后的規(guī)律，從而用理論來指導(dǎo)教學(xué)實踐，更好地培養(yǎng)學(xué)生鑄造國之棟梁.

參考文獻：

[1]趙陽.高中數(shù)學(xué)對物理成績影響的量化研究[J].現(xiàn)代教育科學(xué)，2016（07）：36-42.

[2]劉補云.中學(xué)階段各學(xué)科相關(guān)系數(shù)差異分析及教學(xué)建議[J].考試研究，2016（05）：67-73.

[3]王苑.高中理科生數(shù)學(xué)成績與其它學(xué)科相關(guān)性分析[J].數(shù)學(xué)之友，2016（08）：1-3.

（收稿日期：2020-10-27）