基于網絡流方法的集成電路布線設計
楊尚霖,謝龍韜
(石河子大學 機械電氣工程學院,新疆 石河子832000)
集成電路是利用半導體技術把電子元件集成在一起的具有特定功能的電路,在生活中的多個方面得到廣泛運用。集成電路內的電子元件隨著技術的高速發展,其內的電子元件數目已高達十億級別,因此在制作集成電路時需要依靠專業的計算機軟件,該類軟件統稱為電子設計自動化(EDA)工具。制作分為多步驟完成,制作過程中的一大難點是“布線”問題,即在矩形網格中將器件擺放合適之后,利用金屬線將其相互連接,但引線之間不能相互交叉避免造成短路。本問題主要研究“布線”中的特例“通道布線”,它是指在一個橫向的布線區域,需要連接的方格分布在區域頂部和底部,再利用金屬線將其引腳連接起來。
集成電路的通道設計一直是個NP完全問題,由于它的算法時間復雜度高,過去學者對其求解進行過許多研究。20世紀80年代以來,Nobuo Funabiki等[1]人提出了一種并行算法來解決二層通道布線的設計問題;Jens Lienig等[2]人在此基礎上,采用遺傳近似算法對通道布線問題進行了求解,降低了尋找可行解的時間;隨著集成電路的發展,Chen Y K等[3]對二層通道布線方法進行改進,提出了適用于三層通道設計的布線方法;褚靜[4】、周曉娜[5]研究了圖論在通道布線中的運用;K.Madhavi等[6]、黃訓誠[7]、徐寧[8]研究了現代智能算法在通道布線求解問題中的運用。學者們對集成電路通道布線設計求解算法進行了充分的探討,而對于通道布線問題的數學機理模型的討論較少。在上述研究的基礎上,本文結合網絡流理論構建了用于解決集成電路通道布線問題的單目標優化混合整數線性規劃模型。運用LINGO求解器對于最為常見的二層通道布線設計問題進行求解。最后結合實例說明了模型的可行性,如圖1所示。
1 問題分析
通道布線設計是將對應的引腳用導線相連,在布線的途中不出現串線問題的同時,使布置的導線總電阻值最小為目的的優化問題。對于不同規模的網格,其拓撲結構、引腳位置對求解結果有著十分關鍵的影響。本節針對網格的結構和連線約束兩個方面進行闡述。
1.1 網格結構
(1)網格規模大小直接限制了導線走線,連線不能超出網格。
(2)相鄰網格和網格之間才能用導線連接。
1.2 連線約束
(1)對應各個引腳必須用導線連接。
(2)一層通道內,每個網格只能有一條導線經過,否則存在串線問題。
(3)導線在穿過兩層通道之間時,需在中間安置通孔,通孔對電路電阻有影響。
2 數學模型建立
2.1 符號含義說明
集成電路通道布線設計是將對應的引腳通過矩形網格用導線相連,尋找連線總電阻值最小的優化問題。為了解決此問題,首先需對一些符號進行定義說明,見表1所示。

表1



2.2 目標函數與約束條件

上述模型中,目標函數式表示的是布線總路徑電阻值最小;約束條件反應的是:(2)式要求每條導線的連接是連續的;(3)式表示的是每條線只能經過一個網格一次;(4)(5)式表示的是第1、2層的每個網格最多只能由一條導線經過;(6)式表示通孔的存在條件;(7)式表示每條線的對應引腳起點和終點必須相連;(8)(9)式表示只能用導線連接相鄰的網格;(10)(11)式表示決策變量均為0-1變量。
3 結果分析
通過將不同規模大小、不同引腳個數的集成電路代入模型進行布線設計,通過LINGO求解,分析模型結果的可行性,見表2、圖2所示。
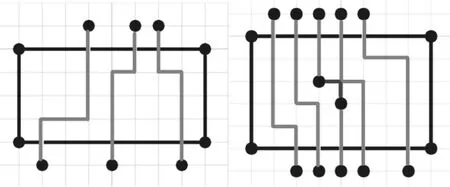
圖2 通過LINGO求解得到的布線效果圖
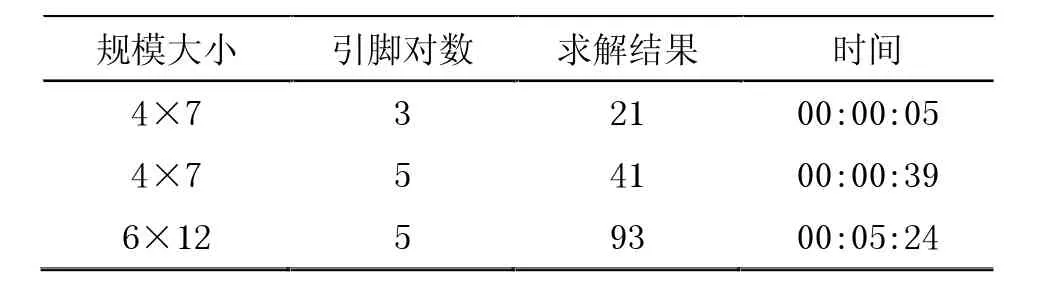
表2 算例求解結果
4 結論
本文針對集成電路通道布線問題進行研究,以布線電阻值為布線主要因素,考慮到布線長度以及通孔個數對于線路電阻值的影響,建立設計了一個以線路電阻值最小為優化目標的數學模型,通過將模型代入LINGO求解得到的結果,可以大大降低布線電阻值,提高了布線電路的性能和可靠性。
本文未考慮線路彎曲對于線路電阻值的影響,線路電阻會由于線路的彎曲而變化,它對電路性能有著很大影響。

