基于M-WFRFT的物理層安全傳輸技術

李 勇，宋志群，王 斌，趙彥惠

(1.通信網信息傳輸與分發技術重點實驗室，河北 石家莊 050081； 2.中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

由于無線傳輸信道的開放性，無線通信的安全問題十分突出，特別是在軍事無線通信系統中，一旦信息被截獲或破解，整個無線通信安全將受到極大威脅，只要在信號傳輸范圍之內，無線竊聽者可以無限制地接收和分析信號[1-4]。

傳統的信息安全主要靠加密算法，例如AES算法，但是隨著未來計算能力的提升，特別是量子計算的出現，加密算法的使用將受到很大限制[4]。

除信息層面的加密算法外，無線通信物理層的安全傳輸也是近年來研究的熱點，典型的物理層安全傳輸技術是基于擴展頻譜算法。例如經典的擴頻和跳頻技術，這兩種技術主要是擴展頻譜，降低信號的功率譜密度，將信號隱藏在噪聲之下，達到信號隱藏的目的。這種物理層安全技術發展的同時，相應的截獲技術也在快速發展，甚至截獲技術的發展更快，因此傳統擴頻技術的使用也受到一定的限制，并且擴頻技術也降低了符號速率[2-4]。

智能天線[5-6]和人工噪聲[7-8]也是物理層安全技術，主要依靠物理層信道特性，達到無線傳輸安全的目的。這需要在硬件上進行改進，代價和成本較高。因此，發展新的物理層安全理論具有重要意義。

近年來，基于加權分數傅里葉變換(Weighted Type Fractional Fourier Transform， WFRFT)的物理層安全傳輸技術得到了發展[9-10]，主要是利用變換階數、變換參數的多樣性，達到信號特征隱藏的目的。經典的WFRFT以四項加權為主，可以表示為4-WFRFT。作者已經在前期發表的論文中通過擴展變換項數，得到了一種多項加權分數傅里葉變換(M-WFRFT)[11]，并且給出了其與4-WFRFT之間的關系。但是M-WFRFT的物理層安全性能并未給出，本文基于此目的，給出了基于M-WFRFT的物理層安全傳輸技術，通過實驗仿真，可以證實本文提出的算法對于物理層安全性能的提升。

為了后文推導方便，將四項加權分數傅里葉變換記為4-WFRFT，多項加權分數傅里葉變換記為M-WFRFT。

1 M-WFRFT技術

滿足f(t)∈L2空間的f(t)多項加權分數傅里葉變換的定義表示為：

(1)

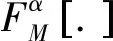
(2)

fl(t)表示4l/M階的4-WFRFT，可以表示為：

(3)

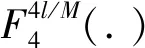
(4)

此外，式中，將α變換成-α，則完成多項加權分數傅里葉逆變換的過程。

本文所提出的多項加權分數傅里葉變換是基于四項加權分數傅里葉變換，二者是否存在某種關系，已經有人證明[11]，并且給出了證明過程，為了后文推導方便，引用此定理：

(5)

以上定理證明了4-WFRFT和M-WFRFT之間的關系，實際上多項加權分數傅里葉變換之間的關系，也可以從上述定理推出。

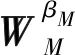
(6)

根據推論1可以看出，對于M-WFRFT和N-WFRFT變換而言(M≠N)，當且僅當式滿足時兩種變換才相等。依據這種理論，考慮設計收發兩端的通信系統模型，如圖1所示。

圖1 基于M-WFRFT的點對點安全通信系統傳輸模型Fig.1 Piont to point transmitting model of security communication based upon M-WFRFT

2 系統模型

本節將依據上述理論設計系統模型，包括相應的幀結構設計，該技術可以應用在以下兩種場景：一是點對點通信，收發兩端的調制密鑰和解調密鑰互異，可以達到物理層安全傳輸的目的；二是點對多點通信，同樣可以利用收發兩端密鑰互異性，每個接收端利用不同的密鑰進行解調。

2.1 點對點安全通信系統模型

為了進一步描述這種安全通信系統，首先給出基于M-WFRFT的點對點通信安全系統傳輸模型。如圖1所示，對于長為N的原始信號X=[x0,x1,...xN-2,xN-1]，假設X是α階的M-WFRFT變換域信號，首先經過基帶映射(BPSK/QPSK)，通過-α階M-WFRFT變換后的信號變為時域信號：

(7)

式中，M>4，并且α∈。

系統中幀結構設計是點對點安全通信系統的重要方面，這能夠保證系統同步以及安全參數的傳遞。下面將著重介紹基于M-WFRFT的安全通信系統的幀結構設計，再經過數模變換后，信號將經過無線信道發送出去。

2.2 幀結構設計

圖2 幀結構設計Fig.2 Designation of frame structure

本文設計的通信系統是處于安全考慮，收發兩端的密鑰互異。如果收發兩端密鑰一致，則退化到傳統的廣義混合載波系統，但是安全性能會受到影響。

在接收端，信號經過模/數變換后，首先進行幀同步，利用直接序列擴頻相關算法得到幀同步信號。經過幀同步模塊處理后的接收信號可以表示為：

(8)

本文關注的物理層安全算法，經過無線信道后的信道均衡算法等，不是本文關注的重點，因此假設均衡算法利用已有文獻的算法已經完成。經過β階的N-WFRFT后的信號為：

(9)

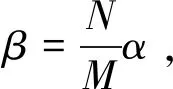
(10)

由上式可知，對于截獲方而言，必須同時已知變換階數(β)和變換項數(N)才能有效解調信號。

2.3多用戶安全通信系統分析

以上主要給出了點對點的安全傳輸模型，由于多項加權分數傅里葉變換的多樣性，很容易擴展到多用戶的場景，在此進行簡單的描述。

假設發送端利用α階的M-WFRFT，發送變換信息，接收端可以有多個用戶接收，需要系統控制每個接收端的接收時隙，并且規定每一個接收端的接收項數。假設有N個接收用戶，每個接收用戶應用的變換為M1-WFRFT，M2-WFRFT， …，MN-2-WFRFT， MN-1-WFRFT，則根據式(6)，接收階數可以表示為β1,β2,...βN-2,βN-1，其中βk表示第k個接收用戶的接收階數，如式(11)表示：

(11)

此處仍需要考慮發送端的幀結構設計，保證不同用戶互不干擾。也可以考慮空間調制技術，保證不同用戶之間獨立接收。本文主要考慮點對點系統，多用戶系統的設計將在后續考慮。

3 數值仿真

本節主要針對點對點系統進行性能仿真，首先針對M-WFRFT可行性進行分析，設計仿真如下：

對于長度為N=128點的sinc信號，不失一般性，采用16-WFRFT進行仿真，發送端的變換階數為3。仿真結果如圖3所示。

假設非合作方也可以截獲發送端的變換項數，但是未知接收端變換項數(假設非合作方的變換項數是4項)的情況下恢復信號和原始信號的對比，可以看出恢復信號和原始信號差別很大，說明本方法的有效性。 由圖3可以看出，收發密鑰互異之后，即使發送接收端的變換階數，由于截獲方只能截獲發送端的信息，也就是可以截獲發送端發送的變換階數與發送端的變換項數，而無法知道接收端變換項數，同樣無法正確解調信號，說明本文提出的基于多項加權分數傅里葉變換的物理層安全傳輸方法的有效性。

以上是對于收發參數互異性的定性測試。下面將針對截獲方或者竊聽者，已知正確解調階數，但是并不知道變換項數的情況，進行誤碼率仿真實驗。假設發射端是用0.25階的4-WFRFT，正常接收端的變換階數是0.5階的8-WFRFT，截獲方或者竊聽者通過截獲手段截獲變換階數0.5，但是接收端的變換項數未知，仿真效果如圖4所示。

由圖4可知，當截獲方或竊聽者的變換項數為16-WFRFT時，相比較于正確變換項數8-WFRFT，誤碼率上升1個數量級；32-WFRFT解調時，誤碼率性能更差，說明本文提出算法的有效性。

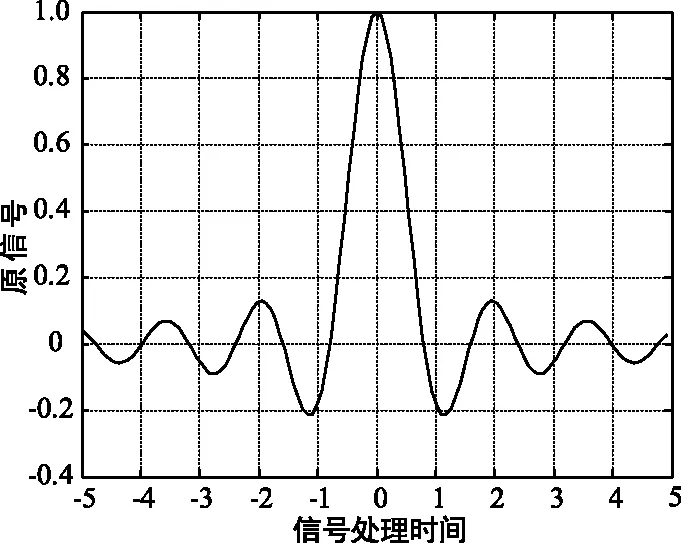
(a) 原始sinc 信號

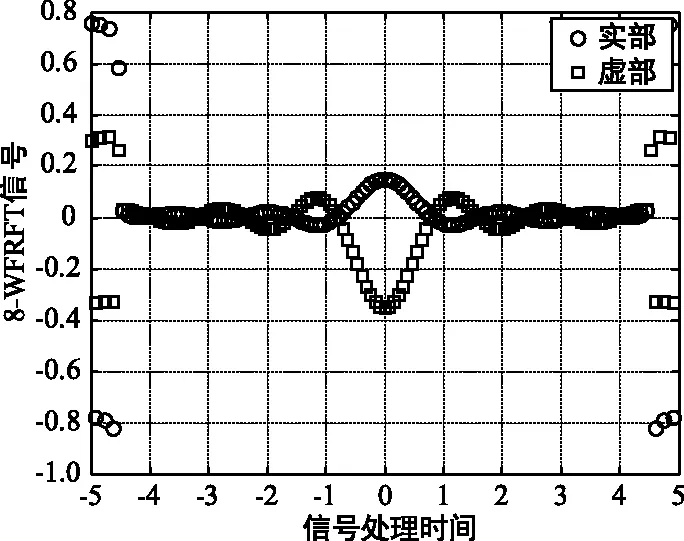
(b) 經過3階16-WFRFT變換后的信號，實虛部信號組成

(c) 非合作方截獲發送階數

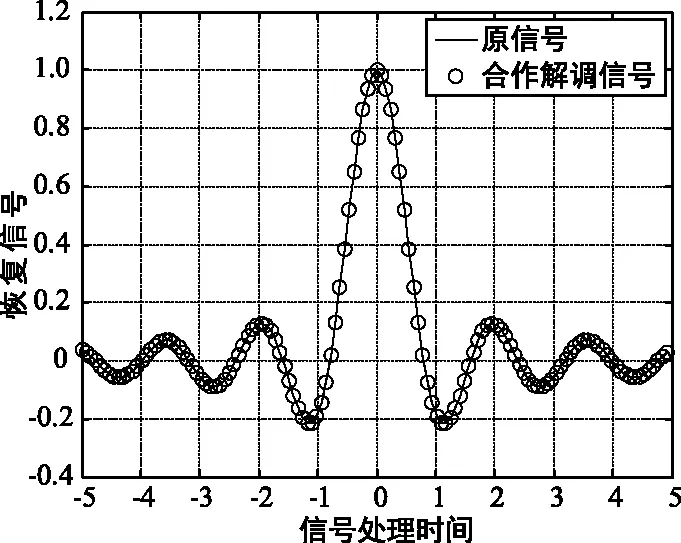
(d) 正確解密過程

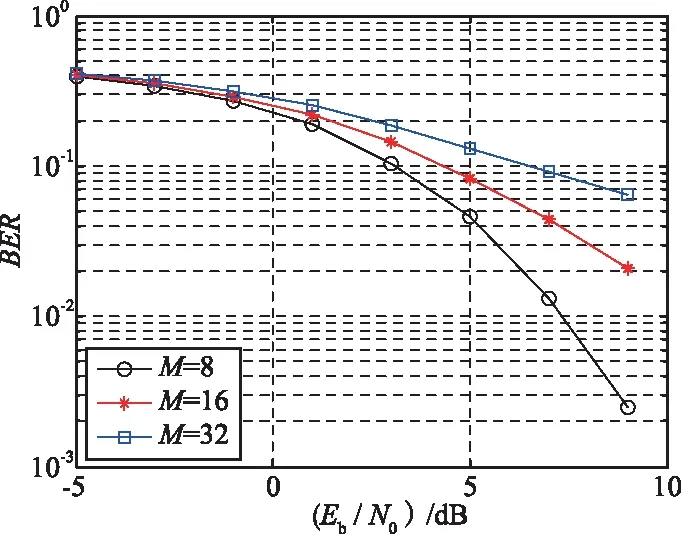
圖4 誤比特率仿真Fig.4 Simulation testing of BER

4 結論

本文針對無線通信物理層安全傳輸問題，提出基于M-WFRFT的物理層安全傳輸技術，其主要貢獻是收發兩端的變換參數可以互異，避免了在接收參數被截獲時信息被破譯的風險。通過數值仿真，在收發變換參數互異情況下，有效避免了信息截獲，物理層安全性能得到進一步保障。