基于GARCH-VaR模型的中國鐵礦石期貨市場風險度量的有效性研究

姚愛萍，丁曉文

(1. 西南大學 經濟管理學院，重慶 400715 ；2. 西南大學 智能金融與數字經濟研究院，重慶 400715)

一、引言

鐵礦石期貨，是以鐵礦石為標的物的期貨品種，利用期貨合約的標準化特性，制定的商品期貨合約。鐵礦石期貨的推出與發展，為全球鐵礦石供應商、貿易商以及終端用戶規避市場風險提供了途徑。作為工業大國，中國一直是全球最大鐵礦石的進口國和消費國，據海關總署披露，2020年，中國進口鐵礦石11.7億噸，同比增加9.5%；對應金額8228.7億元人民幣，同比增加17.4%。兩者均創下歷史新高，但中國在鐵礦石價格方面一直缺乏與消費地位相匹配的影響力。

2020年8月7日，中國鋼鐵工業協會和大連商品交易所組織部分鋼鐵企業召開專題會，計劃在現有交割制度上分批增加一些礦種作為可交割品牌，這些礦種符合交割規范、為市場廣泛接受，旨在更好地為鋼鐵產業服務，由此鐵礦石價格走勢進一步引起社會各方的關注。在現期新冠肺炎疫情對全球經濟影響的大背景下，國際各類資產紛紛下跌，大宗商品也經歷了寬幅震蕩，其中以石油為甚。原油與鐵礦石作為全球兩種重要的大宗商品，它們的價格走勢具有較高的相關性，然而在沙特發動原油價格戰后，在國際原油跌破30美元/桶的情況下，鐵礦石價格依舊堅挺，這無疑對鐵礦石期貨投資者、中國鋼鐵行業的發展等產生巨大影響。鑒于此，本文將GARCH-VaR模型用于鐵礦石期貨市場風險的比較度量研究，選取鐵礦石期貨主力合約收盤價經過處理后的數據建立GARCH-VaR模型，通過似然比(LR)檢驗對比不同分布下模型的精確度。這對期貨投資者投資策略的制定、期貨交易所保證金的設置以及監管部門對期貨市場的合理監管標準的制定等都有重要意義。

二、文獻綜述

(一)期貨市場有效性研究

Garbade和Silber(1983)[1]首先運用實證方法分析商品與現貨市場價格之間的關系，形成了著名的GS模型，后續大量的研究文獻實現了GS模型的擴展。Engle和Granger(1987)[2]提出并發展了協整理論，為市場有效性檢驗提供了一種新的方法，有效地解釋了價格序列的非平穩問題。在此基礎上，Gay等 (2009)[3]利用誤差修正模型分析了基于高頻數據的天然氣期貨價格發現函數，發現期貨價格與現貨價格長期一致性。Milunovich和Joyeux(2007)[4]利用協整檢驗分析了歐洲棉花期貨的現貨價格和期貨價格序列，并發現不同期限的二者存在非平穩序列。

國內學者對于期貨市場的有效性也做過諸多研究。魯瑞榮(2005)[5]通過對大豆和小麥的期貨與現貨價格的擬合檢測，得到大豆期貨市場短期有效而小麥無效的結論；蔣舒與吳沖鋒(2007)[6]則在前兩個品種的基礎上，新增了3個主力品種銅、鋁和膠，通過Johansen協整檢驗、VaR框架下的方差分解進行實證研究，認可了中國期貨市場的有效性。除此之外，還有對具體期貨市場分析，如滬深300股指、黃金等期貨市場的研究[賴文煒和陳云(2015)[7]，季俊偉等(2019)[8]]，研究結果皆表明所研究的期貨市場已經實現了弱勢有效。

(二)期貨市場風險度量研究

在期貨市場的風險度量方面，最初的風險管理工具是JP Morgan公司于1994年提出的VaR模型(在險價值模型)，Wipplinger和Philippe(2007)[9]在他們的文章中詳細地給出了該模型的建立過程，并明確了模型存在的局限性。然而金融時間序列數據往往都表現出尖峰厚尾的特征，基于此Bollerslev(1986)[10]將GARCH模型與VaR模型聯合起來，先利用GARCH模型計算出收益率序列的條件異方差，再運用到VaR值的計算中。Kupie(1995)[11]提出了基于失敗率的回測方法，初步實現了對VaR模型有效性的驗證。Alexander等(2013)[12]則認為過去一些精確的VaR估計值建立在特定的GARCH族模型基礎上，實證結果則獲得了在多個視野和顯著性水平下的準確的GARCH-VaR預測。

鑒于我國的期貨市場屬于新興市場，對其理論研究較少，主要偏重于實證分析。在這些實證研究中，很多學者都用到了GARCH-VaR模型，楊懷東等(2010)[13]在模型的基礎上加入一種新的綜合性流動指標，建立了動態交易保證金模型；劉向麗和常云博(2015)[14]則是將模型用于度量滬深300股指期貨的總體風險。除了GARCH-VaR模型，Realized HAR GARCH模型也受到廣泛應用，蔡光輝和項琳(2020)[15]考慮到滬銅期貨收益所表現的長記憶性，而采用HAR結構提升模型的預測性能，為風險度量和預測提供了新思路。此外還有對不同風險指標估計精度差異的對比實證分析，如王鵬等(2012)[16]運用Backtesting分析對中國金屬期貨市場進行研究。

(三)鐵礦石期貨市場研究

鐵礦石期貨市場研究主要集中在期貨與現貨價格之間的關系以及與期貨價格的定價上。Indriawan等(2019)[17]對我國三種重要的工業金屬期貨展開研究，分析表明螺紋鋼和銅期貨在信息效率方面的可比性，并且要高于鐵礦石，還發現鐵礦石與螺紋鋼期貨之間存在著雙向聯系。Yves Jégourel(2020)[18]回顧了世紀之交以來金融化對鐵礦石市場的影響，并解釋了中國鐵礦石期貨市場的存在，重點分析了這種金融化對于鐵礦石市場的未來乃至采礦業的啟示。Jingjing Tuo和 Fan Zhang(2020)[19]提出一種混合的EEMD-戈魯模型和一種新的數據重構方法，探索中國鐵礦石期貨和現貨市場的價格風險和波動相關性。他們認為中國鐵礦石期貨市場的遠期價格無法充分反映國內鐵礦石期貨市場的變化，因而無法充分傳播國內鐵礦石市場信息。國內研究一般在期貨和現貨價格的波動分析的基礎上做出延伸，基于GARCH、MSVAR等模型，或是加入了市場情緒探究對二者的影響[李莉(2017)[20]，王萌和樊燕萍(2019)[21]]；在與定價有關的研究方面，各學者運用不同的模型與分析方法將國內鐵礦石期貨的國際定價能力作為研究焦點，雖然定價影響力較弱，但對其引導能力逐年增強做了肯定[鄧超和袁倩(2016)[22]，胡振華等(2018)[23]，朱學紅等(2018)[24]]。另外，潘昭帥等(2020)[25]則梳理了鐵礦石主流的定價工具并做比較研究，指數定價仍被視為最重要的定價工具。

通過對國內外文獻梳理后發現，國外風險量化與管理的相關理論體系更加系統與完善，并遠遠領先于國內的研究，現今廣泛使用的一些模型與方法大都是國外的研究成果。對比國內的研究雖然在某些方面有些創新，但更多的是對國外研究成果的應用，并且由于國內外金融市場發展狀況的巨大差異，導致一些風險度量方法并不適用于我們的研究。本文的創新之處在于將國外的風險度量模型應用于我國的鐵礦石期貨市場，基于對日收益率的不同分布假設來找出最適合度量我國鐵礦石期貨市場的模型，這對鐵礦石期貨市場風險管理的進一步研究有重要意義。

三、我國鐵礦石期貨市場發展現狀

在已經具備成熟市場條件的情況下，我國于2013年10月18日在大連期貨商品交易所推出首個鐵礦石品種合約，國內所有鐵礦石供應商皆可參與，隨著交易量的上升，會逐漸吸引國際資本參與國內鐵礦石期貨的交易，進而提升鐵礦石定價機制的話語權。2018年以后，鐵礦石期貨市場加快了對外開放的步伐，繼3月底啟動原油期貨全球化貿易之后，大連期貨交易所于同年5月4日推出以人民幣結算的鐵礦石期貨，這意味著鐵礦石期貨成為第二個邁進國際化的期貨品種。鐵礦石對于我國工業發展的重要性不言而喻，但其需求主要依賴進口這一趨勢中長期內不會改變。

近年來，鐵礦石期貨在人民幣國際化的進程中也貢獻著力量，2020年5月，寶鋼股份與澳大利亞力拓集團在區塊鏈技術的加持下完成一筆總值逾1億元的人民幣跨境結算，其交易標的就是鐵礦石。毫無疑問，大宗商品的結算易于促進人民幣國際化，這也意味著在該領域內國內企業話語權的提高。

圖1 2018年1月—2020年6月大連商品交易所鐵礦石期貨成交量與同期增減百分比

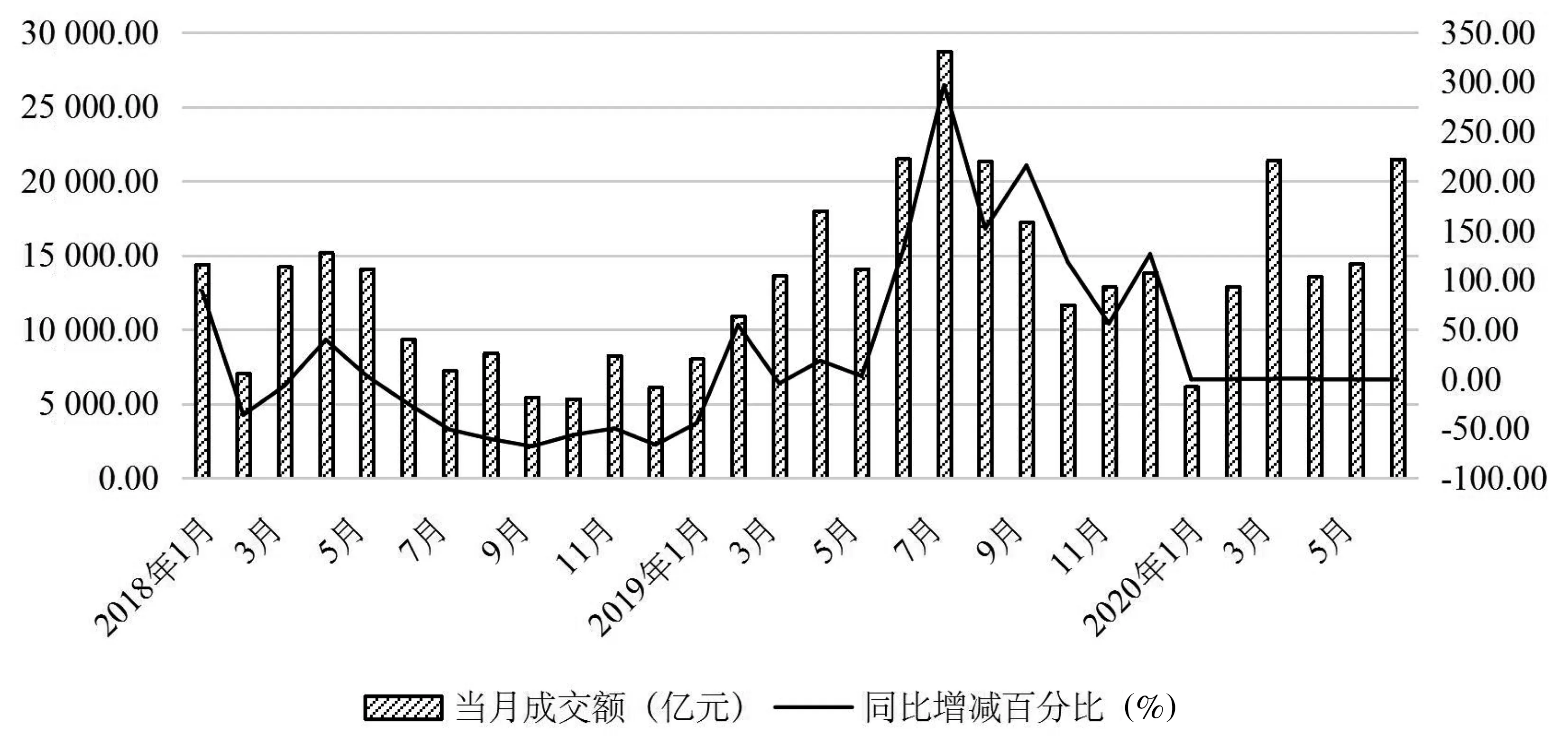
圖2 2018年1月—2020年6月大連商品交易所鐵礦石期貨成交金額與同比增減百分比

根據大商所的數據顯示，鐵礦石期貨在2019年的累計成交總額為19.87萬億元，同比增長72.39%，成為國內成交額最大的商品期貨。如圖1、圖2所示，是2018年1月—2020年6月大連商品交易所鐵礦石期貨成交量與成交金額，在成交量提升幅度沒有超越以往高點的情況下，2019年的鐵礦石期貨成交金額創下了歷史新高，其成交量與成交金額皆在7月達到頂峰，在2020年1月之前同比增減百分比都處于震蕩的狀態。

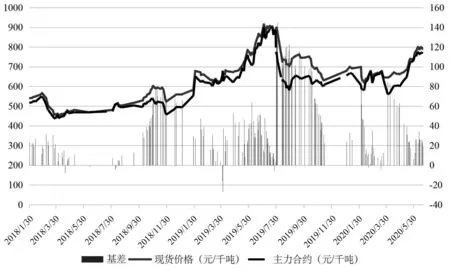
圖3 2018年1月30日—2020年6月19日鐵礦石現貨價格、主力合約價格及基差情況

從圖3可以看出，自2018年1月30日以來，鐵礦石的現貨及主力合約價格上漲明顯，并于2019年7月突破900元/千噸，并在高位震蕩了月余，且基差在此期間的絕大部分時間都是正值。此外，值得關注的是，在經歷了短時間的大幅下降后，從2020年4月開始，鐵礦石需求端持續攀升，截至6月中旬，鐵礦石期貨也從4月初的542元/千噸上漲至752元/千噸。多種因素的作用使得鐵礦石的價格高位震蕩，在海外供應端收縮的情況下，國內對鐵礦石的需求不降反升，國內鋼鐵行業的巨額利潤早已使得海外礦山盆滿缽滿，中國在進口鐵礦石市場的勢力不可小覷。

四、鐵礦石期貨收益率波動及風險的實證分析

(一)數據的收集及統計分析

本文從大連期貨交易所官網(http://www.dlfe.com.cn/)的每日鐵礦石期貨收盤價(除周末與節假日外)，時間從2018年1月30日至2020年6月19日共205個鐵礦石期貨主力合約收盤價，用對數的一階差分rt=lnxt-lnxt-1對收盤價進行處理，得到日收益率。

1.時序圖

本文利用Eviews8.0軟件，對處理后的數據進行描述性統計分析，首先是收益率序列時序圖，如圖4所示。

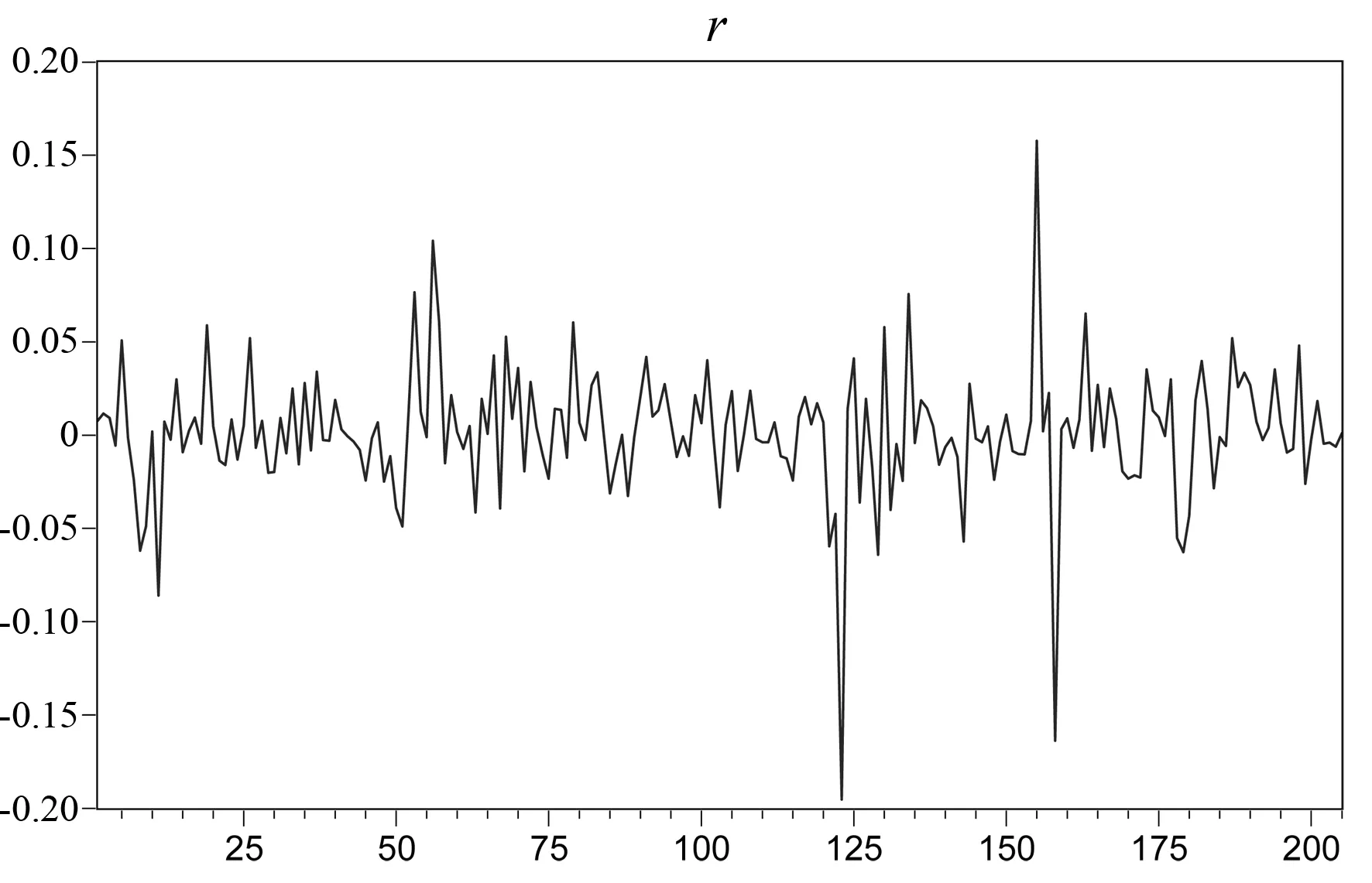
圖4 收益率時序圖

從圖4可知，收益率在0處上下波動，總體來說波動范圍較穩定，但也有幾處波動異常。第一處波動出現在2019年7月29日至2019年8月12日，第二處波動出現在2019年11月12日至2020年2月13日。前者主要是鐵礦石期貨出現遠期合約交換和遠期升水，因為國內鐵礦石期貨是10%的保證金交易，再加上消息面和基本面的影響，一天內可能有100%左右的價格波動，導致出現期貨價格的漲停板。后者的波動則是新冠肺炎疫情的影響，國內封鎖了大部分的對外出口項目，導致鐵礦石價格出現程度比較大的波動。

2.直方圖

由圖5可以看出，序列的均值是0.001367，標準差為0.034270，最小值為-0.195321，數據的偏度為-0.870576，其值小于0意味著序列分布有長的左拖尾，峰度是11.87556，要高于正態分布3的峰度值，說明其日收盤價的收益率序列具有“尖峰厚尾”的特征；Jarque-Bera統計量值達到了698.7702，同時P值為0，故拒絕該對數收益率序列服從正態分布的假設。對于這里的尖峰厚尾，本文之后運用GED分布和t分布來擬合。通過以上檢驗結果，可以分析得出收益率分布顯著地不服從于正態分布，而是出現了具有尖峰厚尾現象，所以本文選擇使用GED分布與t分布來擬合，并且用QQ圖來檢驗。這里以t分布為例，如圖6所示，是在該收益率序列服從t分布的假設下使用QQ圖的檢驗結果。

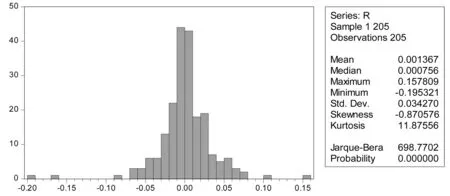
圖5 收益率直方圖

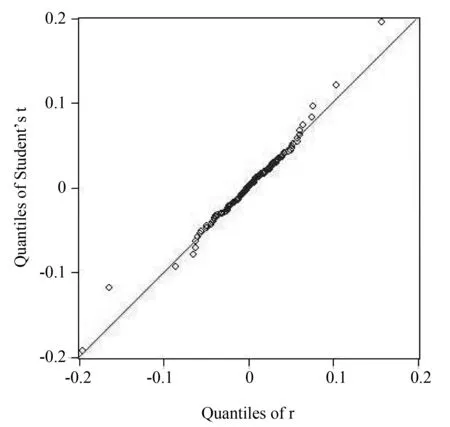
圖6 t分布下的收益率序列QQ圖

據QQ圖所示，t分布描述得很好，在隨后的模型建立過程中，我們以殘差服從t分布與GED分布的假設確定參數來完成GARCH模型的建立。然后研究殘差平方序列的自相關性，為此建立殘差平方序列的均值方程，并用Ljung-Box檢驗確定殘差平方序列的相關性。經檢驗，其值均小于0.05，因此拒絕原假設，判定殘差平方的時間序列具有自相關，具有ARCH效應。

3.平穩性檢驗

接下來對鐵礦石期貨收益率序列進行ADF檢驗，結果如表1所示。

表1 收益率序列的ADF檢驗結果

根據表1中的結果，鐵礦石期貨收益率序列的ADF值為-13.62005，小于1%、5%、10%顯著性水平下的臨界值，對應P值接近0，這表明收益率序列不存在單位根，拒絕序列隨機游走的原假設，認為序列是平穩的，說明我們建立GARCH模型進行實證部分的研究過程是有效的。

4.相關性檢驗

本文通過杜賓-沃森(D-W)和自相關檢驗進行序列相關性檢驗，由杜賓-沃森(D-W)檢驗的結果，鐵礦石期貨合約收益率序列的D-W值是2.003920，約等于2，因此我們可以認為該收益率序列的殘差不存在序列相關性。接下來再對該收益率序列進行相關性檢驗，結果見表2。

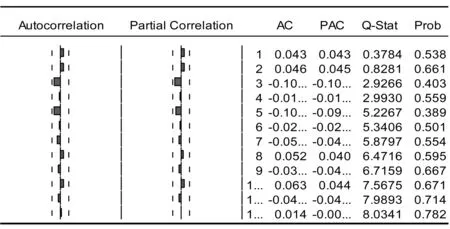
表2 收益率序列的自相關檢驗結果

由表2可知，自相關和偏自相關系數基本都落在兩倍的估計標準差內，且Q-stat統計量對應的P值均大于0.05，故該序列在5%的顯著性水平上不存在顯著的相關性，因而可將均值方程設定為白噪聲，設立模型rt=πt+εt。

(二)建立GARCH模型

1.ARCH-LM檢驗

由于金融時間序列常存在異方差，因此在建立GARCH模型之前，還需判斷收益率序列是否存在ARCH效應，我們依舊使用Eviews8.0來進行下列的檢驗過程，首先對滯后一階的收益率序列進行最小二乘估計，然后對其殘差序列進行ARCH-LM檢驗。

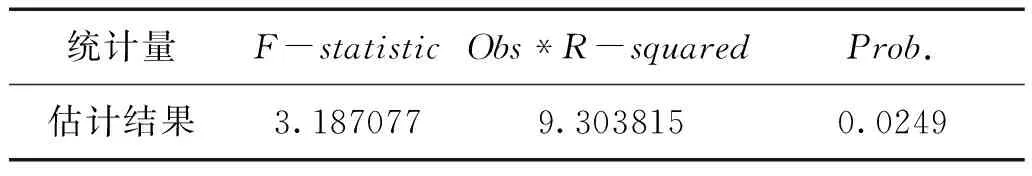
表3 收益率序列的ARCH-LM檢驗結果

由表3可知，在5%的顯著性水平下，收益率序列的F統計量所對應概率小于0.05，故拒絕收益率序列不存在ARCH效應的原假設，從而存在條件異方差。

2.GARCH模型的建立

由上述分析檢驗可知，鐵礦石期貨的收益率序列符合我們建立GARCH模型的條件。再由描述性統計量的分析結果可知，序列存在明顯的“尖峰厚尾”特征，正態分布不能恰當描述其特點，所以本文只給出了GARCH模型在t分布與GED分布下的估計結果。

首先將收益率序列GARCH模型的均值方程設定為白噪聲，然后在t分布和廣義誤差分布下，比較GARCH(1,1)、GARCH(1,2)、GARCH(2,1)及GARCH(2,2)模型產生的AIC和SC值的大小，據此選擇對應的模型。根據GARCH(1,1)、GARCH(1,2)、GARCH(2,1)及GARCH(2,2)模型的擬合結果，得出表4。

基于以上四個不同參數的比較結果，綜合來看選擇GARCH(1,2)-t與GARCH(2,1)-GED模型來擬合擾動方程，具體結果見表5。

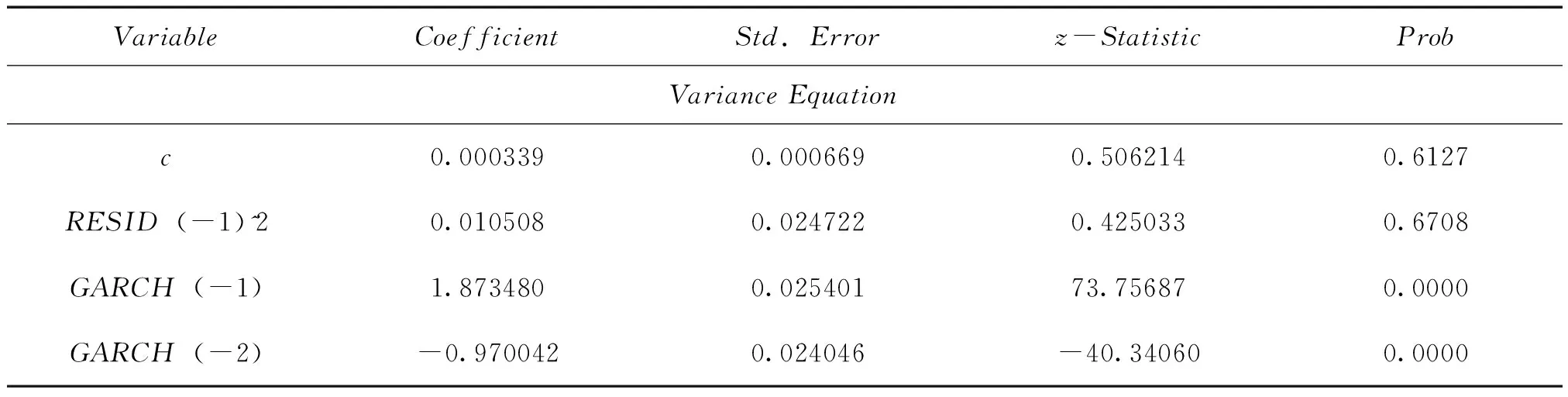
表5 收益率序列的GARCH(1,2)-t模型估計結果

根據表5所示的估計結果得出GARCH(1,2)-t模型的均值方程與擾動方程如下：

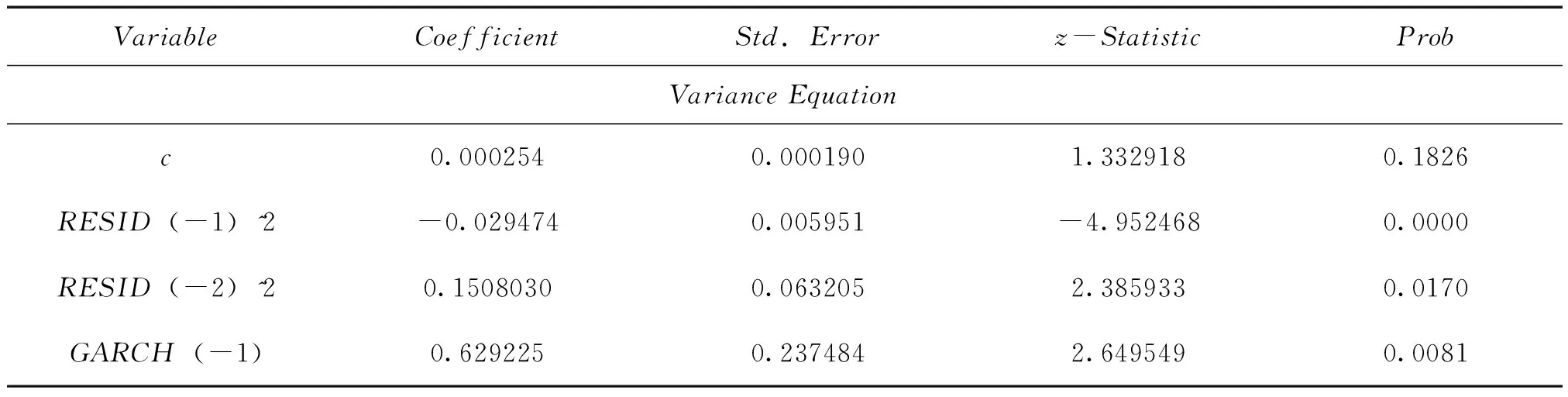
表6 收益率序列的GARCH(2,1)-GED模型估計結果

根據表6所示的估計結果得出GARCH(2,1)-GED模型的均值方程與擾動方程如下：

接著還需要對上述所建立的GARCH模型再次進行ARCH-LM檢驗，觀察模型是否消除了殘差序列ARCH效應，結果如表7所示。

表7 模型建立后的ARCH-LM檢驗結果

由表7可知，在95%與99%的置信度下都不能拒絕原假設，所以本文建立GARCH(1,2)-t模型與GARCH(2,1)-GED模型都成功消除了殘差序列的條件異方差性。

(三)基于GARCH模型的VaR計算與分析

1.VaR的計算

將GARCH模型族與VaR的計算結合起來，也是計算VaR值的一種相對有效的新思路。在Eviews8.0軟件中可以通過對金融資產的收益率序列建立適當的GARCH模型，來完成對收益率序列條件方差的預估，再將其轉化為收益率序列的方差，代入VaR值的公式中，比如計算相對VaR的公式：

便可求得VaR的值。以GARCH-N為例，假設收益率與均值方程的誤差項均服從正態分布，則GARCH模型計算相對VaR值可以使用如下公式：

VaRt=pt-1zασt

其中pt-1為前一時刻股票收盤價格；zα為標準正態分布下的臨界值，通過查表可得，在置信度為95%的水平下，取zα=1.645；σt是根據GARCH模型求出的收益率序列的條件方差。在已知t-1時刻信息集Ft-1的情況下，收益率序列的條件均值和條件方差為：

μt=E(rt|Ft-1)

然而正態分布下的GARCH-VaR模型忽略了股市收益波動的集聚現象，不能反映收益率序列的峰值和厚尾特征，會對VaR的計算精度造成影響。所以我們在計算GARCH-VaR模型時可以考慮其他的分布，本文的研究我們考慮的是使用t分布與GED分布來模擬收益率變化。計算公式也很簡單，在上述正態分布計算公式的基礎上，將zα更改為t分布下在置信水平分位數Tα或廣義誤差分布下的分位數Gα，從而求出t分布與GED分布下的VaR值。

按前文所述，這里對VaR值的計算采用如下公式：

VaRt=ZασtPt-1

計算鐵礦石期貨的收益率序列在95%與99%的置信度下，基于GARCH(1,2)-t與GARCH(2,1)-GED模型的結果，其中Zα是t分布與GED分布在不同置信度水平下對應的分位數；σt是收益率序列的條件方差，再經過開方得到的標準差；Pt是代表金融資產在時刻t的價值，這里我們采用的是鐵礦石期貨在研究區間內的收盤價。除此之外，還需要在t分布與GED分布下的自由度，在上述通過Eviews8.0的模型建立過程中可得到兩種分布下的自由度，分別為T-DIST.DOF=2.191430、GED PARAMETER=0.866964，再有關于不同分布下對應分位數的確定，對此整理出表8：

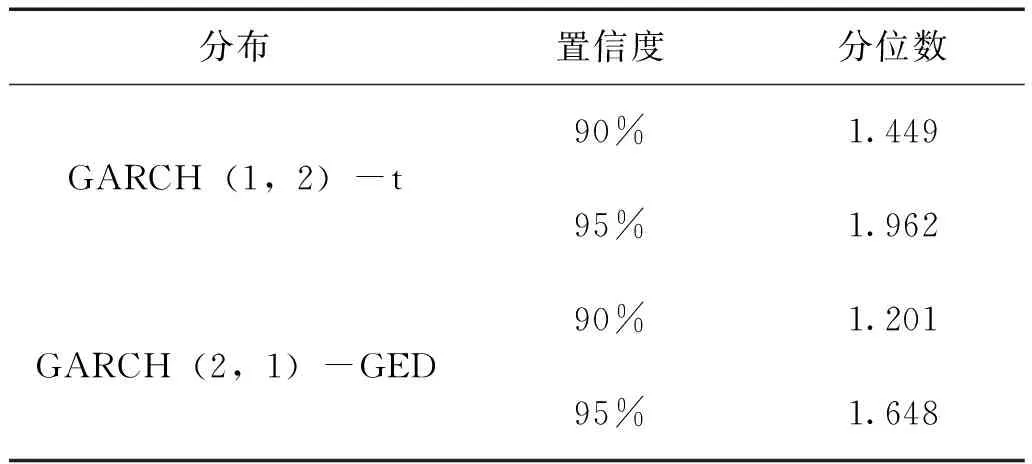
表8 不同分布下的分位數

通過表8給出的分位數，以及在上述過程中得到的GARCH(1,2)-t與GARCH(2,1)-GED模型所預測到的條件異方差序列，代入計算公式即可預測出不同置信度水平下的VaR值。

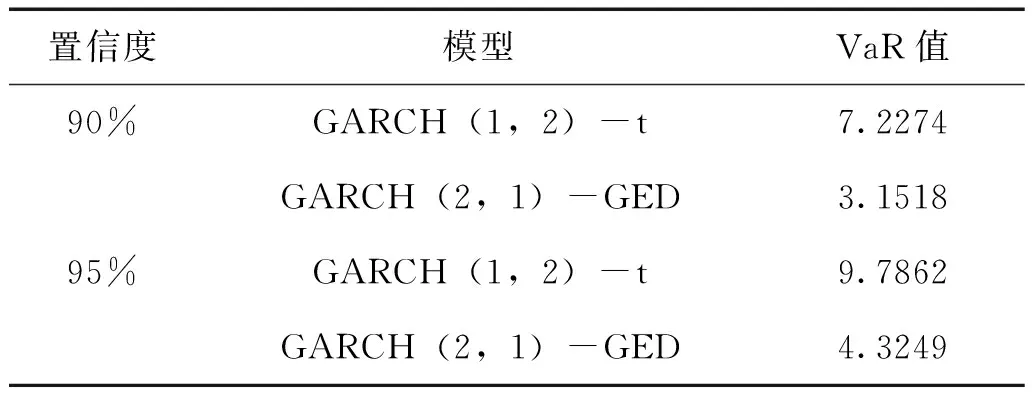
表9 不同模型與分布下預測的平均日VaR值

由表9可以得到：無論是在哪一種置信水平下，GARCH(2,1)-GED模型所預測的VaR值要小于GARCH(1,2)-t模型所預測的VaR值。

2.VaR的檢驗

VaR模型可以加深監管部門和金融機構對當前金融風險的了解，但是模型的建立是否準確，測量精度高不高，還有待檢驗。Kupiec的失敗頻率檢驗法就是其中應用最廣泛的一種，主要思想是得出VaR值超出實際損益的概率，對數據樣本進行返回檢驗，計算溢出天數。基本操作流程如下：

(1)判斷模型是否有效——首先采用似然比來預測和判斷；

(2)判斷模型是否準確——對比失敗率的大小來判斷。

在每個單日失敗的概率不會對其他單日造成影響的情況之下，我們可以將Kupiec失敗頻率檢驗當作一個獨立的伯努利實驗，這里引入虛擬變量Nt，當金融資產真實盈虧大于VaR值時，視為實驗失敗，記Nt=0；當真實盈虧小于所計算出的VaR值時，視為實驗成功，記Nt=1，以此來進行回測檢驗，計算出溢出天數N，具體表述如下：

若要計算置信水平1-c下的VaR值，還要根據溢出天數與樣本容量的比得到失敗頻率p，原假設與備擇假設分別為H0:p=1-c、H1:p≠1-c，下面給出似然比檢驗：

LR=-2ln[(1-p*)T-N(p*)N]+2ln[(1-p)T-N(p)N]

其中T表示樣本容量，N表示失敗天數，p*表示置信水平。和其他統計量相同，LR在不同的置信水平下的臨界值不同，若計算得到的LR值小于臨界值，則接受原假設，說明VaR模型是相對準確的，反之則反。此外，Kupiec還給出如表10所示的接受區間：

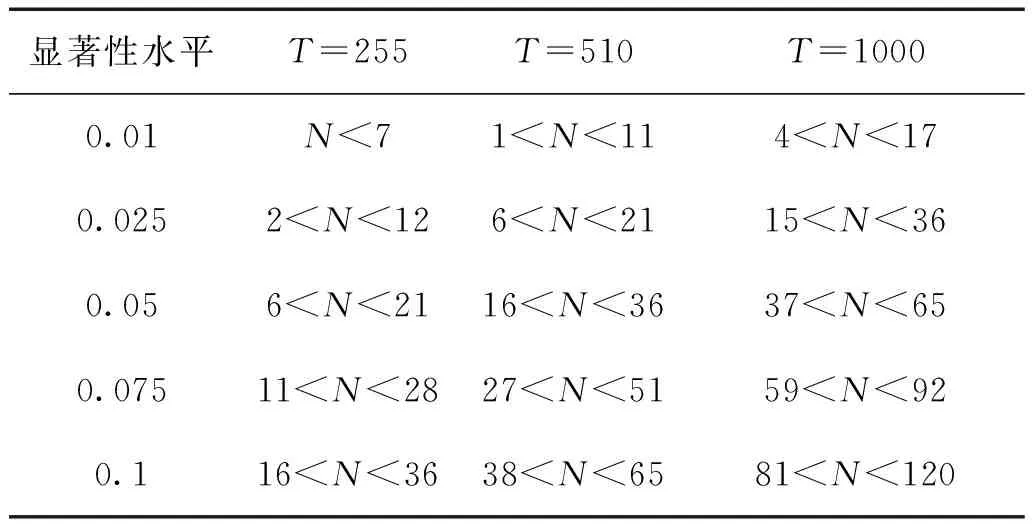
表10 Kupiec檢驗置信域

通過表10可以與實際數據得到的失敗天數作比較，當失敗天數處于置信域時就不能拒絕原假設，反之則反。

按照前述內容介紹的似然比檢驗：

LR=-2ln[(1-α)T-N(α)N]+2ln[(1-p)T-N(p)N]

其中T表示樣本容量，N代表失敗天數，理論上來說，N服從概率為p*=1-α貝努利分布。似然比檢驗的統計量LR～χ2(1)和其他統計量相同，若計算得到的LR值小于臨界值，則接受原假設，說明VaR模型是相對準確的，即

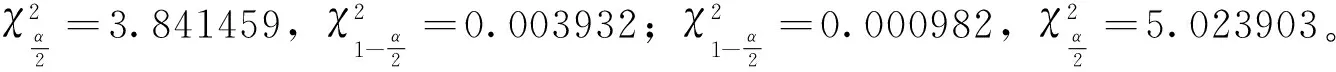
將T=204,P*=α(α=0.1,α=0.05)分別代入LR統計量的公式計算得到統計量的值，表11給出鐵礦石期貨在不同分布下的VaR值的失敗率及失敗天數的有效性檢驗結果。

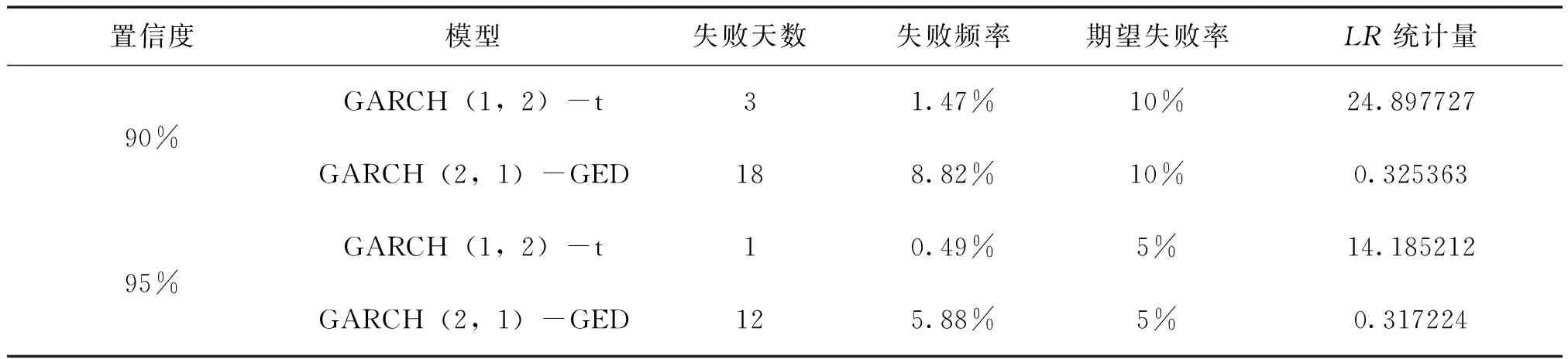
表11 不同分布下的VaR值有效性檢驗

3.結果分析

在前述內容中我們已經通過計算得到：在90%的置信度下，不能拒絕原假設的范圍是0.003932≤LR≤3.841459；在95%的置信度下，不能拒絕原假設的范圍是0.000982≤LR≤5.023903。觀察表11可以得到：

(1)從失敗天數與失敗頻率的角度來看，GARCH(1,2)-t模型下得到的失敗天數較少，導致失敗頻率與期望失敗率相差甚遠，我們認為在t分布假設下對鐵礦石期貨市場風險的度量模型過于保守使得精確度有較大偏差；反觀GARCH(2,1)-GED模型基于失敗天數得到的失敗頻率與期望失敗率相差不大。從該角度我們初步認為GARCH(2,1)-GED模型對鐵礦石期貨收益率的精確度更高。

(2)從LR統計量的計算結果來看，通過GARCH(1,2)-t模型得到的LR值在兩個不同的置信度下均落在了拒絕域，通過GARCH(2,1)-GED模型得到的LR值在兩個不同的置信度下均落在了接受域，通過整理得到表12：

表12 VaR值的LR檢驗結果

在90%與95%置信度水平下的GARCH(2,1)-GED模型均通過了檢驗，我們有理由認為該模型能夠較好地描述鐵礦石期貨日收益率時間序列，較為準確地度量鐵礦石期貨市場的風險，預測效果較好，可以作為風險管理的依據。為進一步評價兩個模型對風險的度量情況，我們更進一步地給出關于所預測的VaR值序列的描述性統計分析結果，如表13所示：

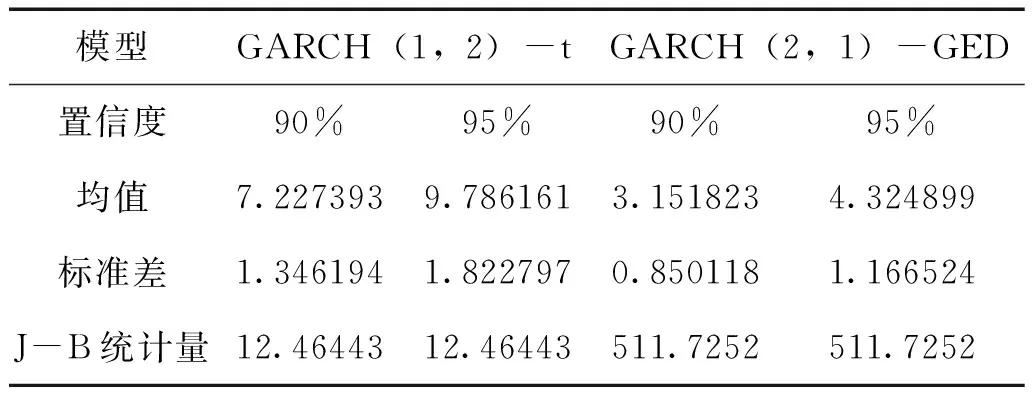
表13 GARCH模型的VaR值描述性統計分析

均值反映了VaR值的平均水平，標準差反映了VaR值的偏離均值的程度，由上表的描述性統計結果可知，GARCH(1,2)-t與GARCH(2,1)-GED模型基于10%與5%的置信水平下，在均值和標準差兩個方面均存在差異。其中在均值方面，GARCH(1,2)-t模型在兩種置信度水平下的預測結果要大于GARCH(2,1)-GED模型所預測結果的2倍，說明后者對預期損失程度的減少，而前者高估了鐵礦石期貨市場的風險；在標準差方面，GARCH(2,1)-GED模型的結果要小于前者，這表明模型所表達的VaR偏離均值的程度也在下降。整體來看，GARCH(2,1)-GED模型要優于GARCH(1,2)-t模型，GARCH(2,1)-GED模型對市場的估計更加接近預期風險值。

五、研究啟示

根據以上研究結論，得出如下啟示：

(1)將VaR方法納入風險管理體系中。結合國外經驗及本文的實證結果，將GARCH-VaR模型納入鐵礦石期貨風險管理體系中具有現實意義。

對于期貨投資者來說，可以利用VaR值來衡量期貨合約未來可能發生風險的情況，通過評估所持有期貨合約的風險值來調整期貨投資組合，將風險控制在自己的承受范圍之內，達到分散和規避風險的目的，規劃好投資策略降低盲目性導致的損失。

站在期貨交易所的角度，VaR方法可用來設定保證金水平，其對期貨交易所和投資者雙方都很重要。若設定值過高，在違約概率降低的同時會增加投資者的交易成本，交易信用雖然得到了維護卻吸引不了投資者；若設定值過低，會導致杠桿效應增大，違約概率增大，不利于整個期貨市場的健康發展。

對監管部門來說，重視VaR方法并將其引進到金融監管中，縮小與發達國家在期貨市場風險管理水平方面的差異，為適應監管部門應對金融市場波動對監管技術提出了更高要求。

(2)進一步發掘和完善期貨市場。中國的鐵礦石期貨市場距離成熟狀態還有很長一段路程，與發達國家的差距較大，各方都應該發掘期貨市場在資源配置、價格發現等功能方面做出努力，提高在預警及抵御風險方面的能力，爭取有朝一日我國鐵礦石期貨市場在世界舞臺上的定價權和話語權。

(3)強化鐵礦石現貨市場的有效性。期貨市場的成熟程度建立在現貨市場是否發達的基礎之上，任何市場都要按照市場機制和價格規律運行，政府應努力建立健全相關法律法規，促進鐵礦石市場化。

(4)建立有效的鐵礦石價格波動預警體系。在當下信息化時代，不妨利用大數據對所收集的有關鐵礦石價格信息來掌握鐵礦石價格的波動情況，隨著國際間交流程度的加深，我國受國際市場的影響程度會越來越深，我們需要一個有效的國際鐵礦石價格預警系統。

(5)注重高級金融人才的培養。進一步落實教育興國、人才強國計劃，培養高素質的風險管理方面的人才，服務于我們的監管部門與各大金融機構，填補我國金融人才缺口。