五步遞進教學法在微積分課程中的應用
李文姿
(山西工程科技職業大學,山西 晉中 030619)
黨的十八大以來,以習近平同志為核心的黨中央堅持把教育擺在優先發展的戰略位置,重點提出堅持深化教育改革創新,堅持深化教育改革創新是我國教育事業實現歷史性變革的根本動力,也是新時代加快實現教育現代化,建設教育強國,辦人民滿意教育的必由之路。在這樣的改革背景下,作為一線教師,如何在教學方法上改革創新成為我們關注的一大問題[1-3]。
另外,大自然中物理現象的分析、神秘的宇宙太空探索、變化復雜的金融市場研究、現代通信技術的發展等等,各種改變世界的高科技,處處需用到微積分的相關知識。而隨著大數據、人工智能技術對自然、社會科學乃至人們日常生活影響的不斷加深,微積分顯得越來越為重要,學習任何一門近代數學或其他許多專業技術都需要先來學習微積分。微積分也成為許多高等學校經濟類、管理類等專業本科學生必修的一門數學公共基礎課程,該課程的學習質量直接影響到學生對后續專業的學習,在培養復合型高素質人才上,具有不可替代的重要作用。然而,由于微積分課程具有難度較大,內容相對枯燥,理論過于抽象等特點[2],導致部分學生對微積分的學習具有畏懼心理,掛科率也較高[3]。如何使微積分的教與學更有成效?只有方法精彩,課堂才能精彩[4],學生才能提高學習興趣,因此如何在微積分教學方法上進行創新改革[3,5],成了微積分任課教師必須思考的問題。本文在微積分教學方法改革方面,提出并應用了五步遞進的教學方法,希望能對微積分的教學有幫助.
一、五步遞進教學方法的內涵與意義
微積分教學中,如果只是教師一味地將概念、定理等知識照本宣科地灌輸給學生,不留給學生充分的主動學習和內化的時間,學生只能感受到微積分就是一堆空洞的文字和符號,不知道其來處,更不知其去處,那么導致的直接結果是學生被動接受知識從而失去學習的興趣。因此,微積分教學方法應致力于從怎么教向怎么學轉變,重視學生為中心,改變過去單純的講授式為主的教學方法,根據教學內容的不同,選擇合適的教學方法,有講授式、啟發式、討論式等,也可采用多種教學方法的組合,本文重點推出“五步遞進”教學法:
從問題出發,引導學生一起分析并探究解決問題的障礙,及時引入所需新知識,精講新知識的重、難點后給予學生內化的機會,并進行小組討論,最終解決問題。這樣的教學方法中,將學生所有的感官進行了充分調動,并將課堂中應有的話語權還給了學生,實現學生主體地位,激發學生學習的主動性。
第一步,聚焦問題,明確目標:我們從實際中尋找與新知識相關的問題,讓學生明確要解決的具體問題,從問題出發,學會梳理問題中的已有條件和缺乏條件,這個過程中讓學生了解到人們的實際生產和生活是需要微積分的,概念、定理的來源是有實際背景的,并在這個過程中學會抽象問題的方法。
第二步,溫習舊知,還原背景:引導學生溫習并運用當前問題所需用到的相關知識,并注意還原知識的背景,做好相關準備工作,揭示微積分概念、公式和定理的實際來源和應用,恢復并暢通微積分與外部世界的聯系。
第三步,結合問題,探究新知:結合要解決的問題學生分組初步探究要解決的問題,并梳理出解決問題的障礙,在此基礎上與老師共同探究還需要用什么新知識來輔助解決當前面對的問題,并及時引入和學習新知識,這個過程中注重突出微積分的基本思想和方法,也要把握微積分課程思政的教育契機。
第四步,應用新知,解決問題:有了新知識的鋪墊后,讓學生小組再次探究解決問題,嘗試給出解決問題的方法步驟,然后與老師共同探究規范解決問題的方法步驟,培養學生應用所學知識解決問題的能力。
第五步,融會貫通,舉一反三:這是強化新知識的過程,融入與所學內容相聯系的、與生產實踐和所學專業結合緊密的實例,讓學生分組解決實例中的問題,給予充分的內化過程,回歸學生在課堂的主體地位,學生可充分體會到數學本身就是刻畫現實世界的數學模型,并非純理論的推導和無處用的游戲。
二、五步遞進教學方法的教學案例——以定積分概念為例
下面我們以定積分概念這節內容為例,來看五步遞進教學法的具體應用。
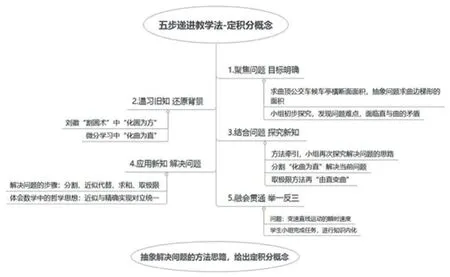
聚焦問題 目標明確:設計某城市的公交車候車亭時對它的容積是有一定要求的,要求出候車亭的容積,首先需要先來求其橫斷面的面積,我們從解決一個曲頂的公交車候車亭的橫斷面面積這樣一個實際問題出發,引導學生抽象出具體問題,聚焦問題即求一個曲邊梯形的面積,這個過程中重點培養學生抽象問題的能力。
溫習舊知 還原背景:面對問題,讓學生分組初步探究,集思廣益,表達出自己的解決辦法,允許思維的獨特性,總結大家的解決辦法,會發現解決問題的難點在于圖形的上方邊是曲邊,面對直與曲的矛盾問題。如何解決直與曲這對矛盾,我們溫習舊知、知識牽引,回顧前面所學的微分的知識中,當時也面臨這樣的矛盾,當時采用了化曲為直再由直變曲的解決辦法。此時,要把握課程思政的融入契機,這種智慧前人在解決很多問題時已經有所體現。比如我國古代數學家劉徽“割圓術”中就有所應用,而且在《九章算術》中也有這樣的記載“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體無所失矣。”讓學生懂得欣賞和感恩,鼓勵學生在今后的學習中善于發現和思考。
結合問題 探究新知:引導學生嘗試用“化曲為直、由直變曲”的辦法來解決當前問題,整個曲邊梯形面積無法直接計算出,那我們就將其先分成若干小的曲邊梯形,每個都近似看成小矩形,也就是將曲線邊近似看作直線邊,為什么分割以后可以近似看作小矩形呢?需要學生去思考,這里應用了連續函數的定義,當自變量變化不大時,函數值變化不大,也就是分割后小區間長度變化不大,其對應的曲邊梯形的高變化不大,可以近似看作小矩形。思考這個問題的同時,能讓學生們感受到,函數連續的概念是有實際應用價值的,不是無用的文字游戲。接著就用所有小矩形面積的和作為所求曲邊梯形面積的近似值。最后,關于如何得到精確值,這是一個從量變到質變的過程,發起討論,學生可以討論各自的解決思路,找到最好的解決辦法是需要將區間分割得無限細,這樣誤差才無限小,此時需要借助極限思想實現“無限”這種狀態,實現由近似到精確的過程。學生們會再次體會到微積分中的概念是用來解決問題的,并非無用的,激發學生學習的積極性。
應用新知 解決問題:結合上面的解決方法和分析思路,先讓學生自己按小組嘗試給出解決問題的步驟,再由老師引導規范解決問題的步驟:分割、取近似、作和、求極限,最終得到解決的結果。在這個過程中,讓學生體會數學中蘊含的哲學思想,近似與精確實現對立統一,解決問題的步驟中,分割、求和式形式邏輯思維的體現,而取極限得到精確值則是高級的辯證邏輯思維的體現與培養。
融會貫通 舉一反三:為了強化新知識,我們會繼續引導學生用同樣的思路去解決另一個實際問題,變速直線運動的瞬時速度,學生分組完成任務,內化所學知識,達到觸類旁通,舉一反三的效果。通過兩個問題的解決,與學生一起比對兩個問題的共性。雖然問題背景不同,但解決問題的思路方法相同,結果的形式也相同。抽象出解決問題的共性,在此基礎上給出定積分的概念。
三、結束語
通過五步遞進的教學方法,有助于實現高階教育目標,學生不僅可以掌握微積分的相關知識、思想和方法,還能更深切感知到微積分中概念、定理的來源是有其實際背景,知道概念、定理的來處,才能知道它們的應用方向。五步遞進教學法的過程中離不開學生小組多次探究解決問題,讓學生積極參與到課堂中來,激發學生學習的主動性和積極性,培養學生學以致用的能力。另外,該教學方法中,注重課程思政內容的有效融入,有助于培養學生的科學素養及創新能力,幫助學生建立正確的世界觀、人生觀、價值觀,讓學生在成長過程中受益終身!

