面向個性化繼續教育的關聯規則挖掘算法研究

胡 悅，羅小楠，王 彬，張 偉

（空軍軍醫大學教學考評中心，陜西西安 710032）

近年來，隨著社會教育水平的不斷提高，繼續教育的需求逐年增加[1]。利用互聯網發展的紅利，實現互聯網+繼續教育的模式是繼續教育行業的一個新的趨勢[2-3]。為了更優地提高繼續教育的教學水平，滿足不同人群的需要，面向個性化繼續教育研究新方法成為一個研究熱點。在個性化推薦方面，關聯規則挖掘算法在諸多領域均得到了應用[4-6]。文獻[7]提出利用關聯規則算法，實現高校圖書館書籍個性化推薦。文獻[8]利用學生信息進行關聯規則挖掘，在教育管理系統上實現了個性化管理。相似的，文獻[9-10]分別利用關聯規則模型建立了銀行產品個性化推薦模型和醫療用品推薦模型。這些研究和應用在一定程度上說明了關聯規則算法可以實現個性化的方案推薦，能夠挖掘數據間的關聯關系。

為了進一步提高關聯規則算法的性能，針對算法的改進也得到了廣泛的研究[11-12]。文獻[13]基于MapReduce 計算模型對關聯規則算法改進進行了總結。針對基于關聯規則的數據挖掘方法，文獻[14-15]分別提出利用模糊邏輯規則和聚類方法提高關聯規則挖掘的算法性能。此類算法改進在較大程度上可以提高關聯規則挖掘的準確性，為個性化推薦提供依據，但在非確定性屬性關聯情況下仍需研究新的方法[16]。

該文面向個性化繼續教育方案優化的需求，研究了關聯規則挖掘算法。在構建個性化繼續教育方案的基礎上，文中利用關聯規則算法，通過建立強關聯規則和頻繁項集，實現數據屬性的關聯規則挖掘。為了獲得更準確的強關聯規則，該文利用DBSCAN 聚類算法進行不確定聚類數目的自適應規則聚類。通過仿真試驗與數據分析，說明所提算法相對于現有算法規則聚類結果更加合理，在個性化繼續教育方案優化方面，具有更高的實用性。

1 系統模型

繼續教育個性化是目前的發展趨勢，為了滿足大規模用戶人群的個性化繼續教育的需求，文中提出基于關聯規則挖掘算法的個性化繼續教育優化方案。其可以有效挖掘不同用戶群體的需求與期望，根據用戶自身情況進行個性化教育優化，方案架構設計如圖1 所示。

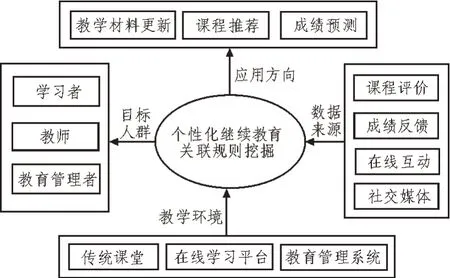
圖1 個性化繼續教育方案架構

文中設計的基于關聯規則挖掘的個性化教育方案架構主要分為目標人群、應用方向、教學環境和數據來源4 部分。

1）目標人群。個性化教育方案的目標人群主要包括學習者、教師和教育管理者3 種，教育管理者與教師根據個性化數據挖掘為學習者制定個性化教育方案；

2）應用方向。個性化教育主要可以應用于教材更新、個性化課程制定推薦和學生成績預測等，針對學生的個人情況和課程匹配程度制定學習方案；

3）教學環境。除了在傳統課堂教學環境上進行應用，個性化教育還可以應用于線上教育平臺和教育管理系統；

4）數據來源。進行個性化繼續教育數據挖掘，需要保證數據的充分性和多樣性，數據來源主要包括課程評價、學生成績反饋、師生在線互動以及社交媒體上的評價，通過多種渠道確保數據的多元性。

2 算法架構

文中提出的面向個性化繼續教育的關聯規則挖掘算法的架構如圖2 所示。算法流程分為數據庫準備、數據預處理、關聯規則建立、產生頻繁項集和關聯數據挖掘5 部分。

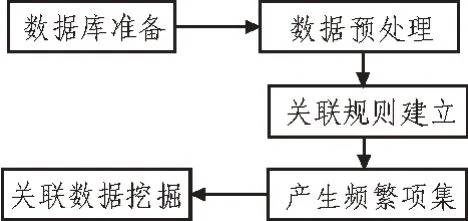
圖2 關聯規則挖掘算法架構

基于關聯規則的數據挖掘，首先需要建立挖掘數據庫，將需要挖掘的數據放入數據庫中。在準備好原始數據后，需要進行數據預處理。預處理內部如圖3 所示，數據預處理的效果在較大程度上影響算法的挖掘效果和運行效率。

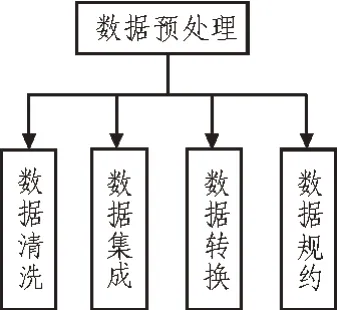
圖3 數據預處理架構

建立關聯規則是算法的核心，在若干可組合規則中選擇具有最大影響的核心規則，可保證數據挖掘結果的有效性。與關聯規則有直接關系的是頻繁項集，兩者是互偶關系。在若干屬性中確定最頻繁出現和結果關系最大的屬性，才能建立正確的關聯規則。確定完兩者后，即可對預處理后的數據進行數據挖掘。如圖3 所示，數據預處理架構主要包括數據清洗、數據集成、數據轉換和數據規約4 部分。

3 個性化關聯規則挖掘

面向個性化教育的數據挖掘算法設計，首先需要建立關聯規則。其是指由事件X必然可以導致事件Y的發生，事件Y是事件X的結果，事件X是事件Y的原因，即X?Y。

假設所有預處理后的數據集合為D，事件X?D，事件Y?D，且X?Y=φ。若有X?Y，則事件X與事件Y之間存在關聯規則。

關聯規則可分為強關聯規則和弱關聯規則，根據規則的支持度和置信度來進行劃分。關聯規則的支持度是指同時包含集合X和集合Y的事件數量與數據集合中D事件總數之比：

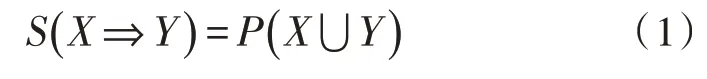
置信度是指集合中同時包含集合X和集合Y的事件數量與包含集合X的事件數量之比：

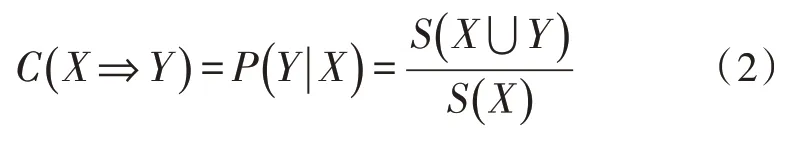
設最小支持度與最小置信度為Smin和Cmin，若規則的支持度與置信度可以同時大于最小支持度和最小置信度，則此規則為強關聯規則；否則，為弱關聯規則。

為了制定個性化的繼續教育方案，需要對數據進行分類，文中提出基于聚類算法對數據間的關聯規則進行分類。數據集合中的數據由事件、事件子集和關聯規則等元素組成，對數據進行聚類，需要計算集合元素間的距離。

設數據庫中任意兩個事件I1和I2，其中I1∈X，I2∈Y，則I1與I2之間的距離定為：

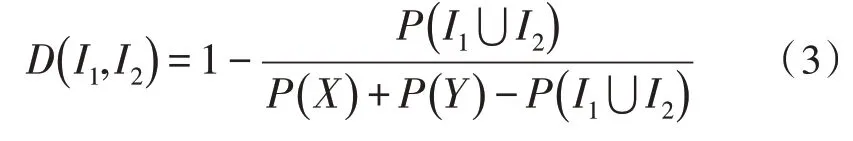
事件之間的距離定為兩個事件同時發生的次數占所有包含I1或I2的事件數目之比，其取值范圍為0～1，即兩個事件總是同時發生，其距離為0；兩個事件完全無法同時發生，則其距離為1。

設事件集合X與Y分別包含m和n個元素，則兩個事件集合的距離定義為集合內所有元素的平均距離，即：

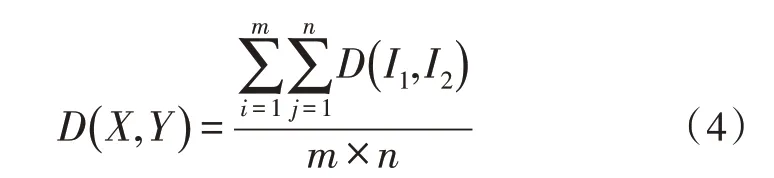
事件集合之間的距離范圍為0～1。

關聯規則之間的距離定義較為抽象，設數據庫存在規則r1和r2，其規則定義可表示為：

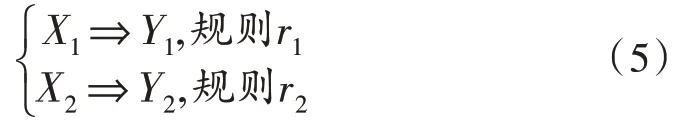
則r1與r2之間的距離可定義為：

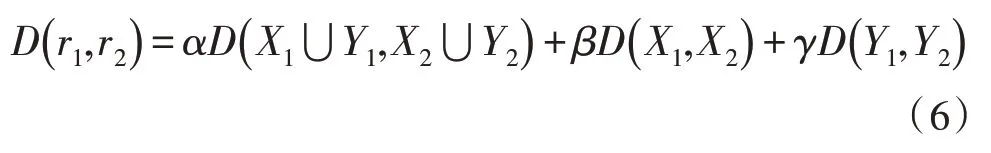
其中，α、β和γ是自定義調節參數，可根據實際數據情況進行調節，對參數進行歸一化處理：

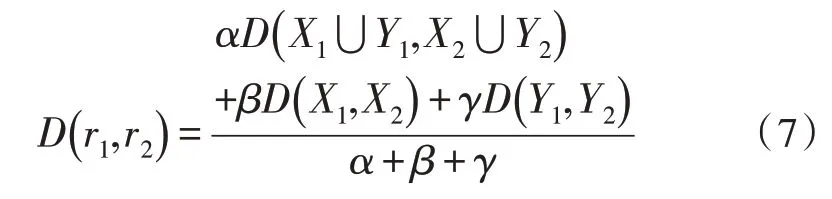
為了簡便分析，一般使自定義調節參數之和為1，α+β+γ=1。

隨著計算機技術的不斷發展與完善，計算機病毒問題也變得越來越棘手。計算機病毒的防范是一個綜合的系統工程，它主要包括了對單個計算機系統與整個網絡的病毒防范過程。如果想要對整個計算機網絡進行防范就必須要進行統一的管理，首先必須要使用統一的網絡病毒查找軟件，這個軟件能夠及時準確地對網絡中的病毒進行識別并及時的做出相應的處理。第二，網絡殺毒軟件要對整個網絡進行殺毒處理，這些軟件也要能夠在沒有人工干涉的條件下自動升級，自動對病毒進行深層次的消毒處理，保證網絡系統的安全性與穩定性。

為了實現關聯規則挖掘，文中提出利用DBSCAN 聚類算法進行分類，并使用輪廓系數來評估聚類算法的性能，輪廓系數的定義為：

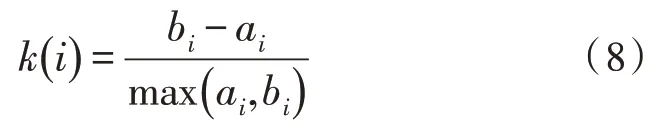
其中，ai表示樣本i到同一規則集合其他樣本的平均距離，bi表示樣本i到其他任一規則集合樣本的平均距離。式（8）可以改寫為：

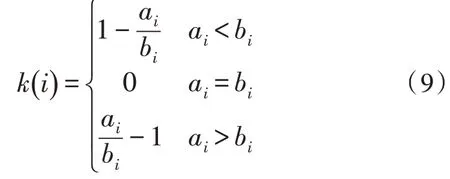
由式（9）可知，輪廓系數取值范圍為-1～1。輪廓系數越接近于1，說明該樣本屬于該規則集合的概率越大；輪廓系數越接近于-1，說明該樣本屬于該規則集合的概率越小。當輪廓系數為0 時，該樣本屬于兩個規則集合的概率相等。

文中提出的DBSCAN 聚類算法流程，如圖4 所示。其中，可達規則密度是指在規則可達半徑內的樣本數目。

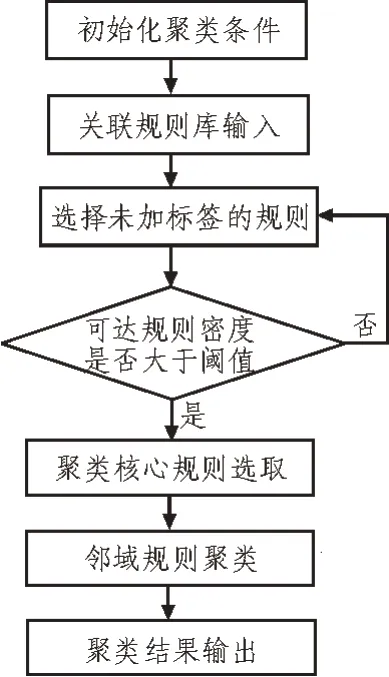
圖4 DBSCAN聚類算法流程圖

面向個性化繼續教育的需求，文中設計了基于DBSCAN 聚類的關聯規則挖掘算法，其步驟如下：

1）輸入：數據集合g，最小聚類數目Nmin，可達密度閾值e；

2）隨機確定聚類中心Ci；

4）將元素i從數據集合g中剔除；

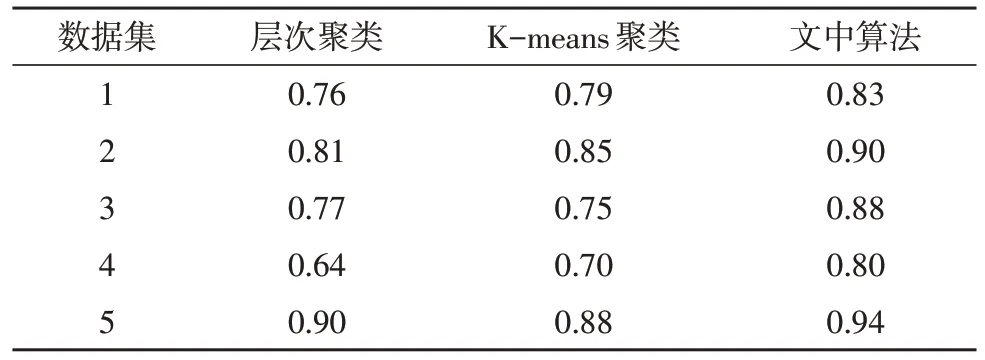
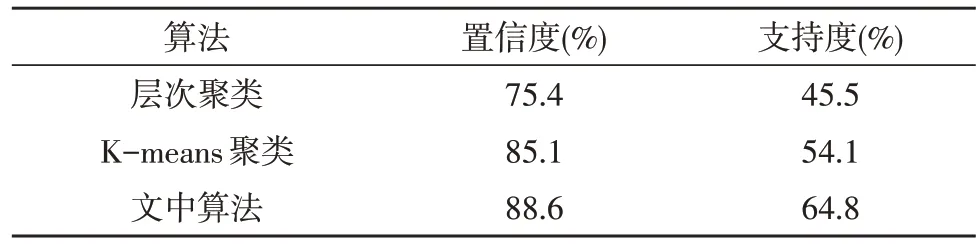
5）若N（Ri）

6）計算集合中元素j到聚類中心的距離εij；

7）若εij≥e，則繼續執行步驟8）；否則轉到步驟9）；

8）將元素j加入到關聯集合Ri；

9）將元素j從數據集合g中剔除；

10）j=j+1；

11）生成若干個數據類別集合{Ri}；

12）輸出：數據類別集合{Ri}。

4 仿真驗證及數據分析

為了驗證所提的面向個性化繼續教育的關聯規則挖掘算法的有效性，文中通過對比現有算法與所提算法的聚類輪廓系數，比較聚類算法的合理性。另外，通過分析對比不同聚類算法下的關聯規則置信度和支持度，說明了所提算法的有效性。

如表1 所示，該文在5 個不同數據集上進行關聯數據挖掘，對比層次聚類算法、K-means 聚類算法和文中所提的DBSCAN 聚類算法的聚類輪廓系數。整體上看，K-means 聚類算法略優于層次聚類算法。但在部分情況下，由于K-means 聚類算法的聚類中心數目錯誤，導致其性能反而低于層次聚類算法。文中所提算法在不同數據集合上的輪廓系數均高于其他兩種算法，說明聚類結果更合理。

表1 不同算法聚類輪廓系數對比

如表2 所示，在同一數據集下，該文對比了基于3 種聚類算法的關聯規則挖掘算法的置信度和支持度。文中所提算法的關聯規則置信度與支持度均高于層次聚類算法和K-means 聚類算法，說明文中所挖掘的關聯規則屬于強規則，利用所挖掘的規則可以更智能地進行個性化繼續教育方案優化推薦。

表2 不同算法關聯規則置信度和支持度對比

5 結束語

為了滿足個性化繼續教育方案優化的需求，基于關聯規則挖掘算法提出了一種智能的個性化繼續教育方案制定技術。利用DBSCAN 聚類算法實現數據集內聚類中心數目不確定情況下的自適應聚類，并根據聚類結果提取核心規則進行個性化繼續教育方案優化。通過仿真分析證明，所提算法相對于現有聚類算法，聚類結果更合理，且具有較高的魯棒性，而且該算法可以挖掘的規則關聯性更強，在繼續教育方案優化領域具有良好的實際應用價值。