雷達信號偵察處理系統研究

蚩建峰

(解放軍92785部隊，河北 秦皇島 066200)

1 緒 論

電子戰接收機是電子情報偵察體系和干擾機中的重要組成部分，它的主要功能是接收復雜信號環境下的非合作信號[1]。電子戰接收機需要能適應現代高密集的信號環境[2]，對接收到的大量信息必須實時或準實時地進行處理，其偵察接收結果的性能直接影響電子對抗干擾的效果。最主要的特點[3-4]有：(1) 寬輸入帶寬；(2) 高靈敏度；(3) 高的測頻精度和頻率分辨率；(4) 大動態范圍；(5) 處理同時到達多個信號的能力。

如圖1、圖2所示，傳統的模擬式信道化接收機把瞬時帶寬劃分成相互交疊的多個信道，每個信道對應1個模擬濾波器，對每個濾波器的輸出信號檢測之后，判斷信號駐留于哪個信道，后面再進行AD采樣和識別、參數測量等信號處理。獲取的雷達基本特征參數包括：載波頻率、脈沖寬度和幅度、脈沖到達時間等。干擾機根據雷達參數進行干擾決策，以獲取最佳干擾參數。傳統的接收機不僅體積龐大，結構也比較復雜，而且由于某些器件本身是非線性的，導致接收機下變頻后的基帶信號相位有偏差，從而影響接收結果的判斷和后續處理。因此數字化信道接收機[5]近年來被廣泛使用，由于干擾機目前主要是采用現場可編程門陣列(FPGA)實現信號的偵收處理，因此本文重點研究易于FPGA實現的相關處理算法[6]。

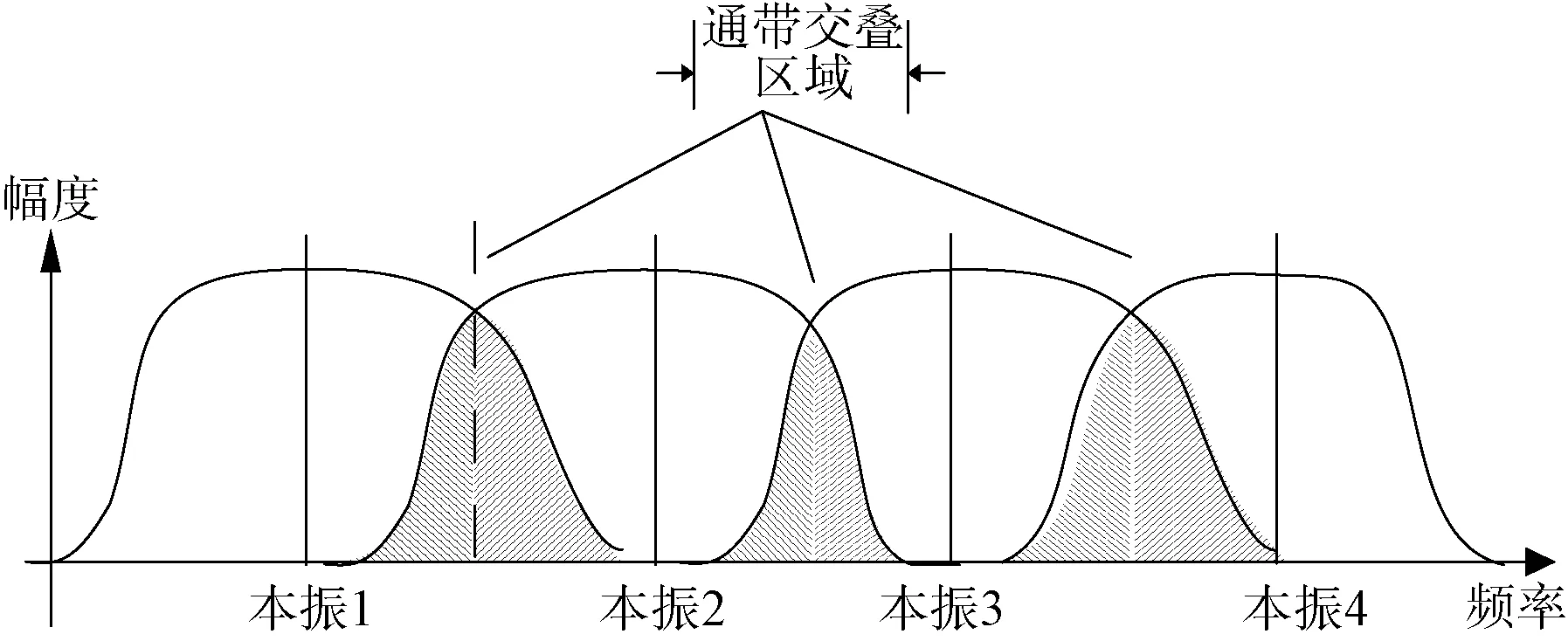
圖1 模擬信道化示意

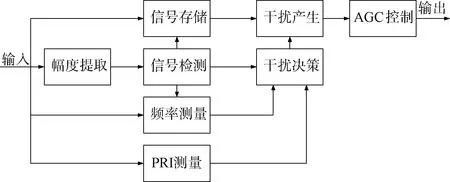
圖2 偵收處理模型

2 信號檢測原理及實現方案

信號檢測實現雷達信號的檢測、幅度信息提取，為后續同步存儲以及實現相關干擾時序(如間歇采樣、假目標、距離波門拖引等)服務，瞬時測頻接收機(IFM)也需要檢波信號引導接收機工作。

檢波性能的好壞直接影響著干擾機對雷達信號的判斷，以及后續的處理性能。檢波分為模擬檢波和數字檢波，模擬檢波方法具有溫度性差和檢波線性不好等固有缺陷，且檢波的精度低，丟失了信號的相位信息，一般作為模擬信號檢測引導使用，在接收機中一般采用數字檢波的方法。

2.1 檢波原理

理想的正交下變頻后，I，Q兩路信號可表示為：

si(t)=rcosφ(t)

(1)

sq(t)=rsinφ(t)

(2)

由公式(1)、(2)可以得到：

(3)

(4)

在FPGA中，用查找表的方式很容易實現反正切函數和求平方根函數，而且可以達到很高的精度。為了減少存儲空間，可以在查找表中完成信號功率與閾值比較的運算，輸出為0或1的檢波結果。用查找表方法實現如圖3所示。

圖3 用查找表求幅度法檢波

但是在使用查找表的時候，由于存儲空間的限制，也不能完全使用IQ兩路數據的全部16 bit數據。例如對于8 bit的模數轉換器(ADC)，需要16位的只讀存儲器(ROM)地址。這么大的查找表在FPGA上很難實現。一種易于實現的方法是對I、Q數據舍棄低m位，近似為：

(5)

(6)

舍棄低位，會使算出來的幅度值并不是1個常數，通過固定檢測門限后，會使檢波結果存在1個閃爍區。

另外一種簡單的算法是利用I，Q兩路數據的絕對值的最大值來近似代替信號的幅度，如圖4所示。

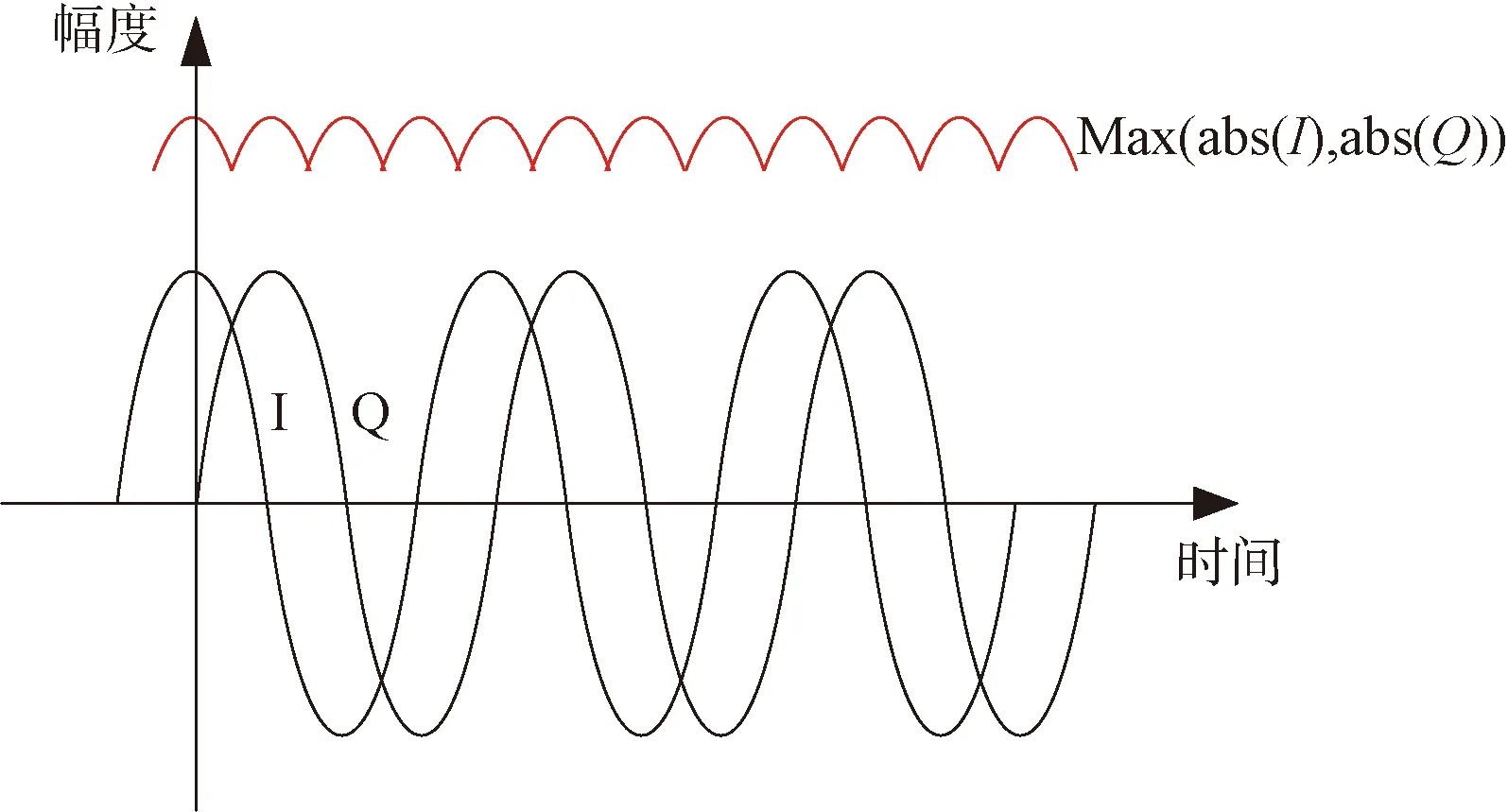
圖4 用Max(abs(I)，abs(Q))來近似信號的幅度

具體實現方法如圖5所示。

圖5 用絕對值最大值法檢波

用比較器就可以直接實現，運算資源占用較少。但是由于I，Q數據的絕對值的最大值是對信號幅度的近似，存在凹坑，會引起檢波閃爍的現象。如圖6所示，I，Q相等點的幅度與信號幅度相差3 dB，即存在3 dB的幅度閃爍區。

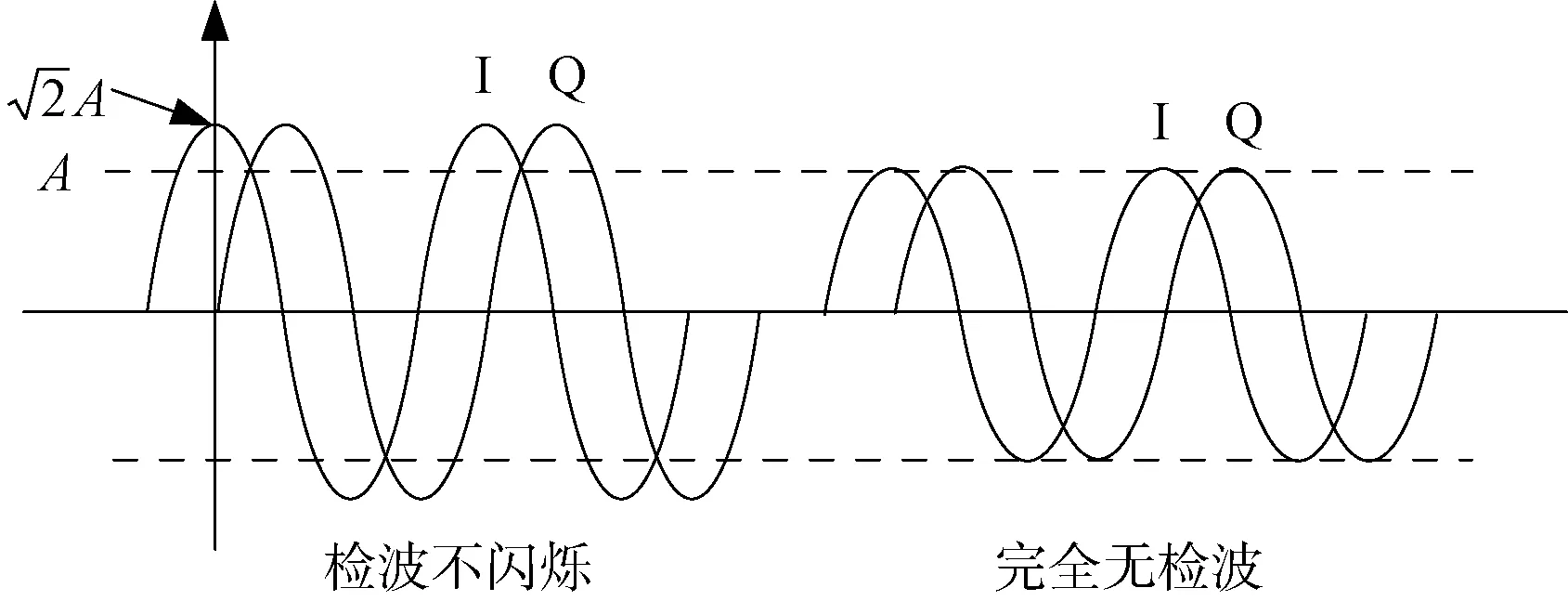
圖6 近似算法帶來檢波閃爍原因示意

2.2 遲滯比較器

對于幅度判斷,如果只設定1個判斷閾值，則會出現如果輸入幅度為門限時，由于噪聲和幅度測量誤差的影響，輸出的檢波信號來回閃爍，如圖6所示。使用遲滯比較器就可以解決這個問題。

遲滯比較器輸出狀態的轉換取決于輸入信號的變化過程，它有2個判斷門限：輸入信號從低電平上升的過程中，對應的檢測門限為上門限；輸入信號從高電平下降過程中，對應的檢測門限為下門限。另外由于遲滯比較器內部存在正反饋，所以輸出電壓波形的邊沿很陡。遲滯比較器檢測過程如圖7所示。

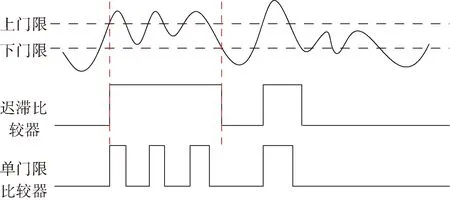
圖7 遲滯比較器和單門限比較比較器效果比較

2.3 脈寬濾波

脈沖寬度濾波器也稱為計數濾波器，主要采用計數的方法來實現數字濾波。由于干擾機工作靈敏度較高，信號檢測門限較低，同時受散熱和收發隔離等影響，其內部會存在噪聲的尖峰干擾，有可能超過信號檢測門限，但是通常其幅度不穩定，持續時間較短，因此根據先驗知識，當脈寬小于某一設定值時，不可能是真實的雷達信號，應給予濾除，從而抑制尖峰干擾。這也就是脈寬數字濾波電路的工作原理。

當原始輸入信號由低變高后，基準時鐘信號開始被計數，當檢測到的脈沖寬度小于一定的值(如200 ns)時，確定為尖峰干擾，不予輸出，當輸入信號寬度大于預置濾波寬度時，濾波器輸出方波供后序電路處理。濾波脈寬的選擇是影響計數頻率濾波器濾波效果的關鍵，脈寬太小，部分尖峰干擾信號不能濾除；太大將會丟失有效的雷達信號，所以應用中應根據實際現場情況，選擇適當的濾波脈寬。

如果當前檢測到2個有效的雷達信號脈沖，并且2個脈沖之間的間隔小于一定的距離，則認為可能是接收機內的噪聲或者其他因素導致的同一個雷達檢測信號的中斷，需要將其作為同一個信號。

脈寬濾波的實現與遲滯比較器類似。即其上門限為脈沖寬度大于a，判斷脈沖有效，其下門限為低信號脈寬大于b，判斷脈沖結束。

3 測相測頻原理及實現方案

測相測頻的作用主要如下：

(1) 采用快速測頻的方法，在檢波有效內測出當前輸入信號的粗測頻率，用于判斷當前頻率是否位于零頻或者多信道交疊區域，用來輔助后續電路操作。

(2) 粗測雷達信號的形式，以及是否存在多雷達信號，用來輔助后續干擾設計：

(a) 在偵收的完整脈沖內，測出起始頻率和終止頻率，如果其差值大于一定的值，則判斷為線性調頻信號，否則為單載波信號。以選擇相應的干擾模式；

(b) 在每個脈沖前沿測出其起始頻率，并判斷它與上一個脈沖起始頻率差值是否超過一定的值(如5 MHz)。如果超過，說明當前空域存在多雷達信號或者雷達存在頻率捷變；

(c) 在偵收的完整脈沖內，檢測每個采樣點之間的角頻率差值，如果角頻率差值大于一定的值(如2/3π)，則判斷雷達采用二相編碼信號。

3.1 測頻原理

可見，在dt時間內測出相位的變化值，就可以得到頻率的值。為得到頻率的值，首先需要求出相位的值。可以使用查找表法根據公式(3)或者是CORDIC算法求相位值，這里使用CORDIC算法。測頻實現方案如圖8所示。

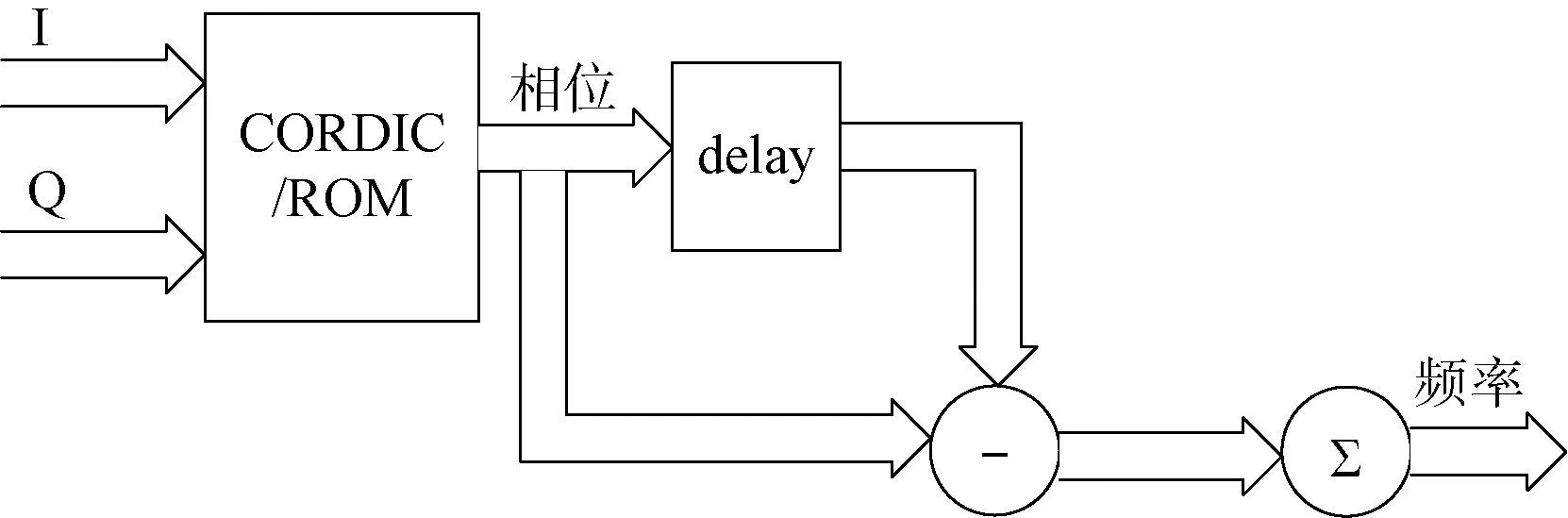
圖8 測頻實現方案

3.2 測相原理及實現方案

對于某向量的角度，CORDIC算法通過對一系列固定角度的旋轉將該向量逼近坐標軸，通過將旋轉的角度值疊加獲取選擇的角度，從而間接獲取原始向量的角度。CORDIC算法旋轉示意圖如圖9所示。

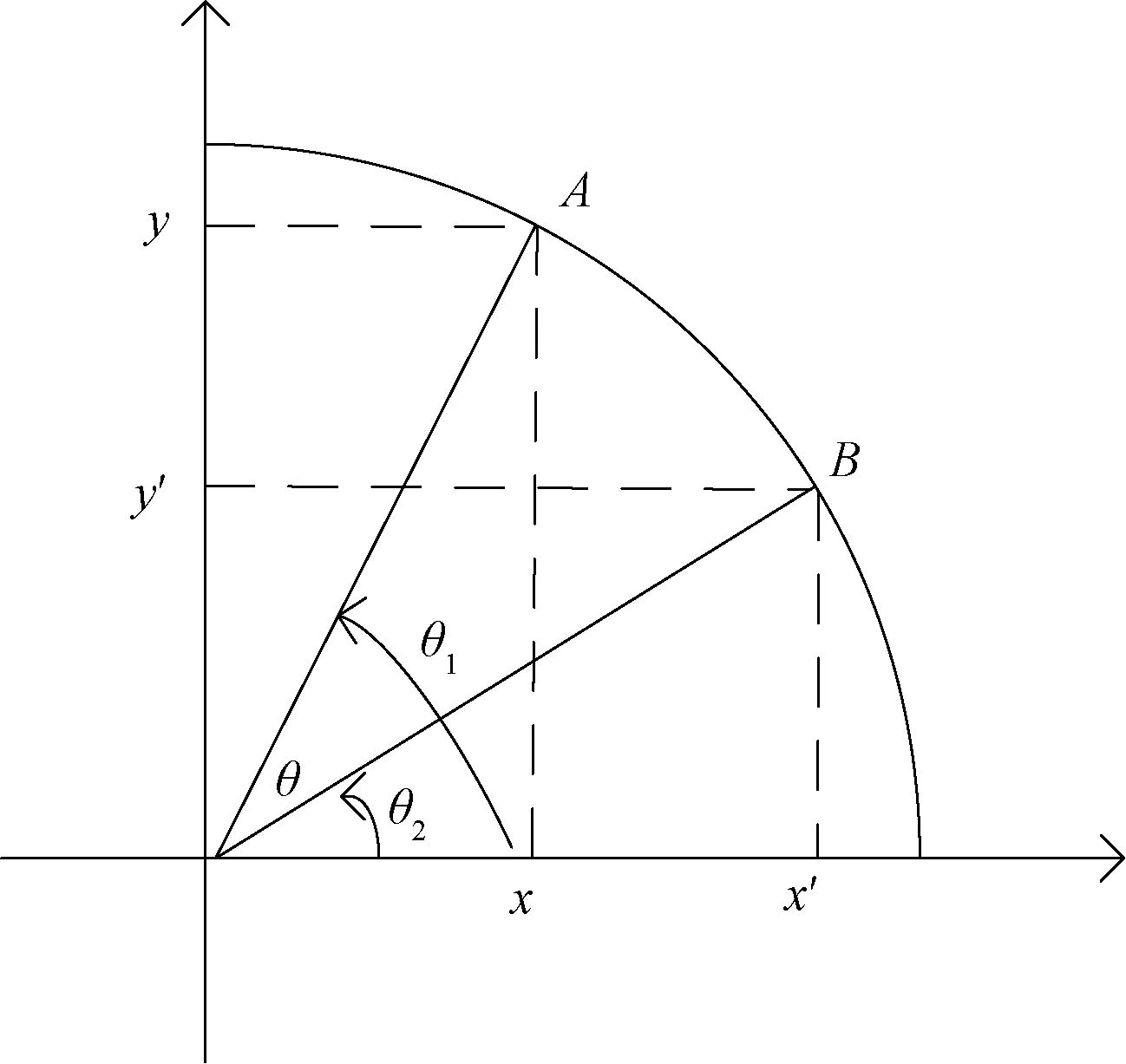
圖9 CORDIC算法旋轉示意

設|A|=r，則x=rcosθ1，y=rsinθ1，θ=θ1-θ2，x′=rcosθ2=cosθ(x+ytanθ)，y′=rsinθ2=cosθ(y-xtanθ)。

假如每次旋轉θi，當tanθi=2-i，公式中的乘法操作就可以轉化成相應的移位操作。y的符號決定下次旋轉的方向，即要求靠近x正半軸，用σi表示，當y′=0時，中間每次旋轉的角度和θi就是所求的相位。在每次旋轉的時候，可以將前面的乘積項cosθ部分提取出來，不參與運算，這對于旋轉的角度并沒有影響。如果需要得到真實的幅度值，可以對結果再加以校正。這樣，每次迭代的公式為：

(7)

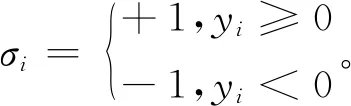
可以看出，x，y相當于每次都移i位后進行加(或減)運算，而z則是每次加(或減)arctan(2-i)的角度。

n次迭代后，變為：

(8)

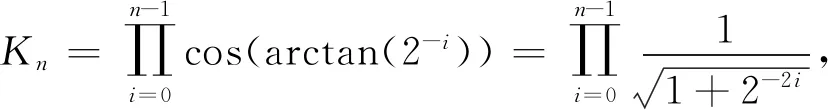
由于第1次迭代時旋轉了arctan(20)，旋轉角度總和在-π/2和π/2之間，這個限制導致當要計算角度絕對值大于π/2時，需要增加旋轉。可以多增加2次45°的旋轉。

如果需要獲取真實的幅度值，可以將xn的結果乘以Kn得到。

對于8 bit的數據，如圖10所示，由于增加2次45°旋轉，在流水的方式下，結果的輸出要延時10個時鐘周期。

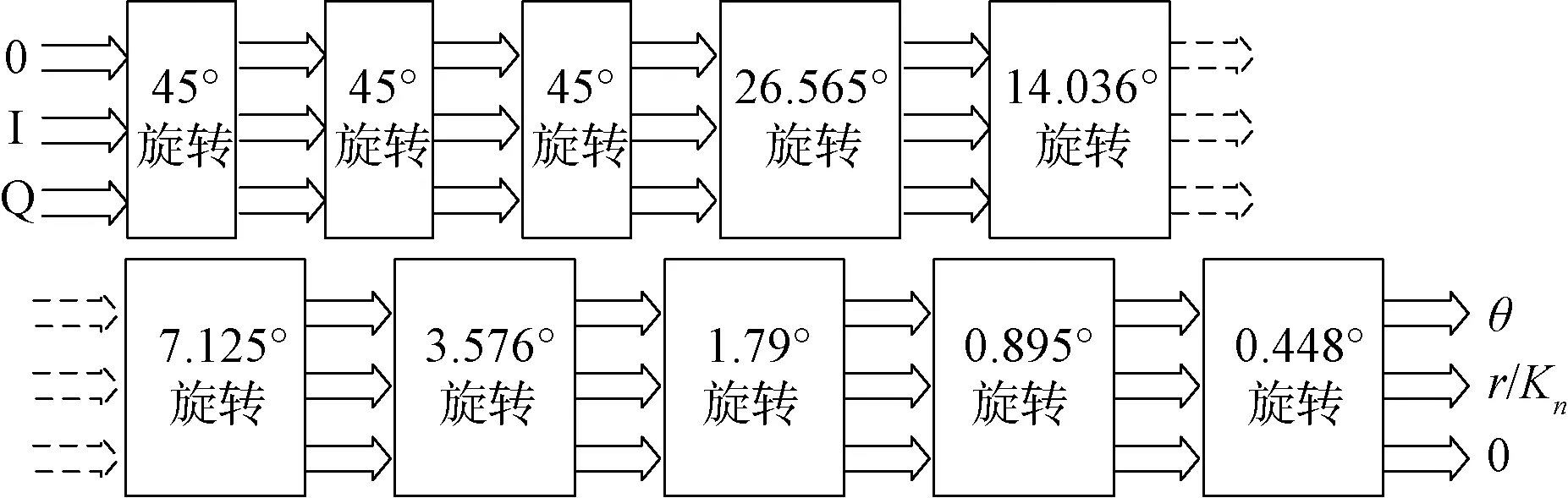
圖10 每次旋轉角度

CORDIC算法實現可分為迭代結構和流水結構兩種，其中流水結構是以面積來換速度。干擾機的接收機中考慮到系統實時性要求，一般采用流水結構，如圖11所示。

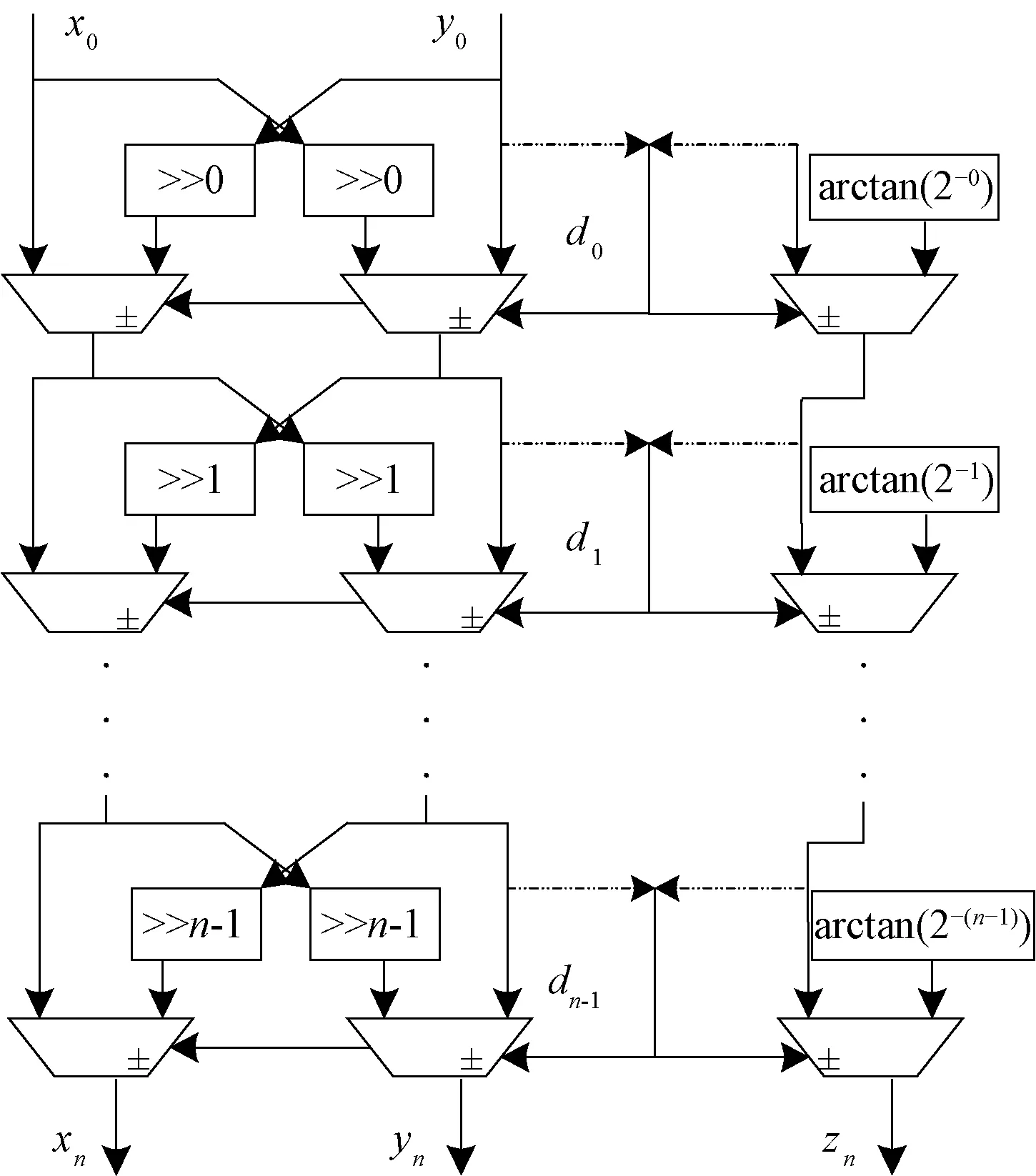
圖11 流水結構實現CORDIC算法

實際應用中，對于800 MHz的采樣率，dt=1.25 ns，則：

Δθmax=360°·fmax·Δt=180°

即對于400 MHz以下的頻率，最大相位差在±180°內，不存在相位模糊的問題。

4 數字AGC原理及實現方案

對于常用的信號存儲轉發的干擾模式，它存在的一個問題是，其輸出功率取決于輸入功率。由于射頻接收前端需要有很大的動態范圍，通常在30 dB左右。而數字射頻存儲器(DRFM)的輸出信號功率則要求超過一定的值，才能實現對于目標雷達的有效干擾。

DRFM中一種解決措施是不使用AGC控制，此時為了保證小功率輸入信號的輸出功率，接收端的放大器需要很大的增益，這樣容易造成大輸入信號時放大器飽和，或者AD/DA削頂失真，導致諧波分量和雜散顯著增大，影響干擾效果。

另外一種措施是使用AGC控制。在接收的雷達信號與干擾輸出之間實現自動增益控制。AGC系統由幅度測量和可變增益放大器組成。幅度測量部分從ADC輸入的信號中提取幅度，自動調節可變增益放大器的增益，當輸入信號幅度增大時，反饋回路控制其增益按一定關系減小，減小時，其增益則按一定關系增大。這樣無論輸入信號強弱，經AGC放大后都能得到電平基本恒定的輸出信號，從而保證整個系統的動態范圍。數字AGC的反饋部分由數字處理實現，與模擬AGC相比，數字AGC降低了調試難度而且增強了穩定性、收斂性和精確性。

5 數字信道化原理及實現方案

模擬信道化雖然在一定程度上稀疏了每個信道的脈沖流密度，但是在單個信道內，由于其帶寬較寬，還是存在寬帶接收機中較難解決的同時到達信號的處理問題。對于同時到達信號，其幅度和頻率的測量都會有較大的誤差，導致后續處理性能下降，而采用數字信道化的方式可以較好實現對同時到達信號的處理。

如圖12所示，借鑒模擬信道化的思想，數字信道化接收機是使用1組濾波器把接收機的整個工作帶寬劃分成若干個小塊，每個小塊稱為1個信道，接收到的信號經過濾波器組以后，不同頻率的信號會在不同的濾波器輸出，即在不同的信道輸出。每個信道輸出的信號是1個窄帶的帶通信號。對每個信道輸出的窄帶信號進行頻譜搬移，變成低通信號。為了降低信號后續處理的速率，可以對每個信道的低通信號進行抽取。

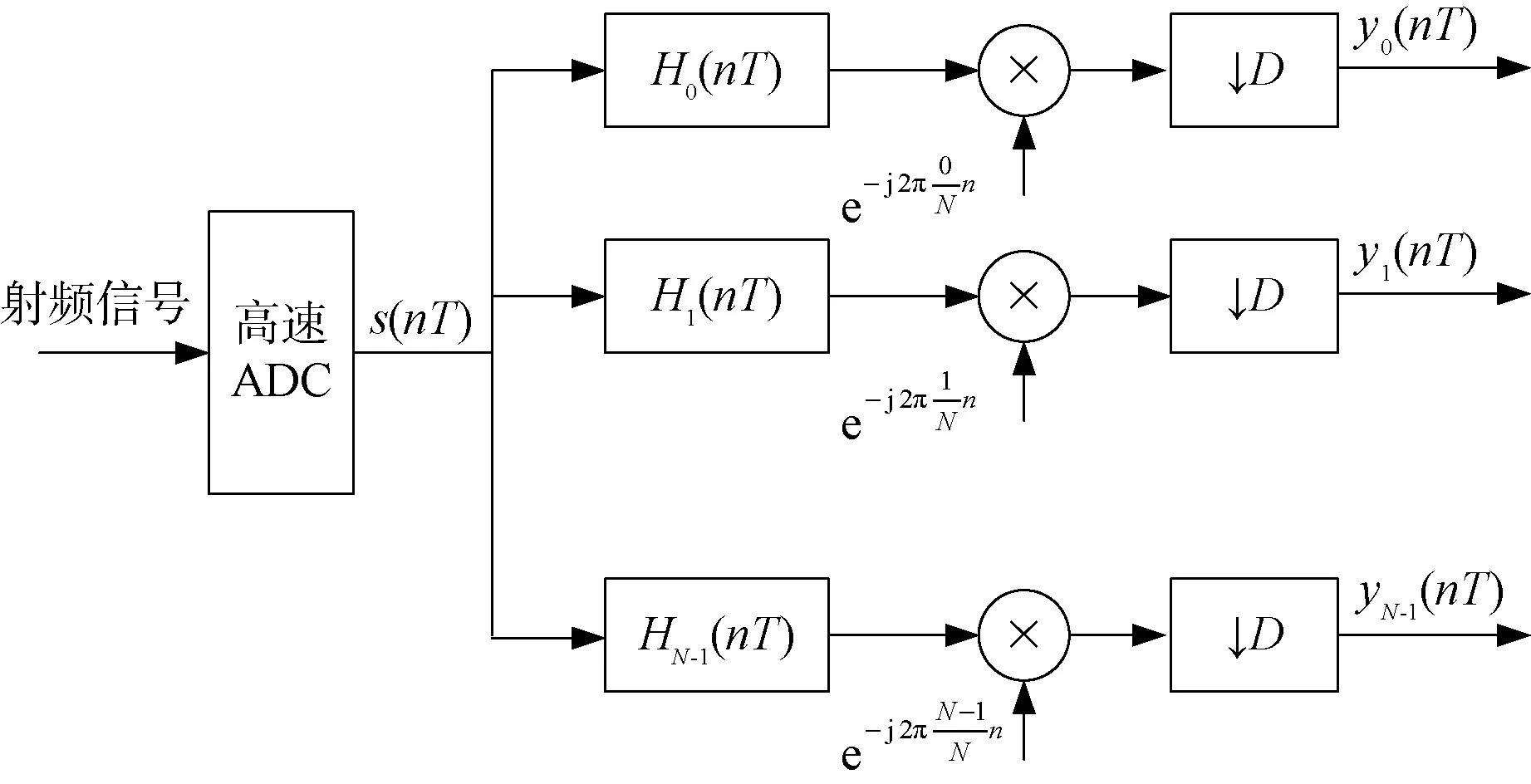
圖12 通過帶通濾波，然后進行下變頻的信道化接收機結構

這種結構的信道化接收機信道的劃分比較靈活，通過設計不同的帶通濾波器，就可對信道進行不同方式的劃分。這有利于在使用過程中根據實際需求對信道進行靈活劃分，可以只對有用頻段的信號進行處理，丟棄不關心頻段的信號。

等效結構如圖13所示，先進行下變頻，然后進行低通濾波。

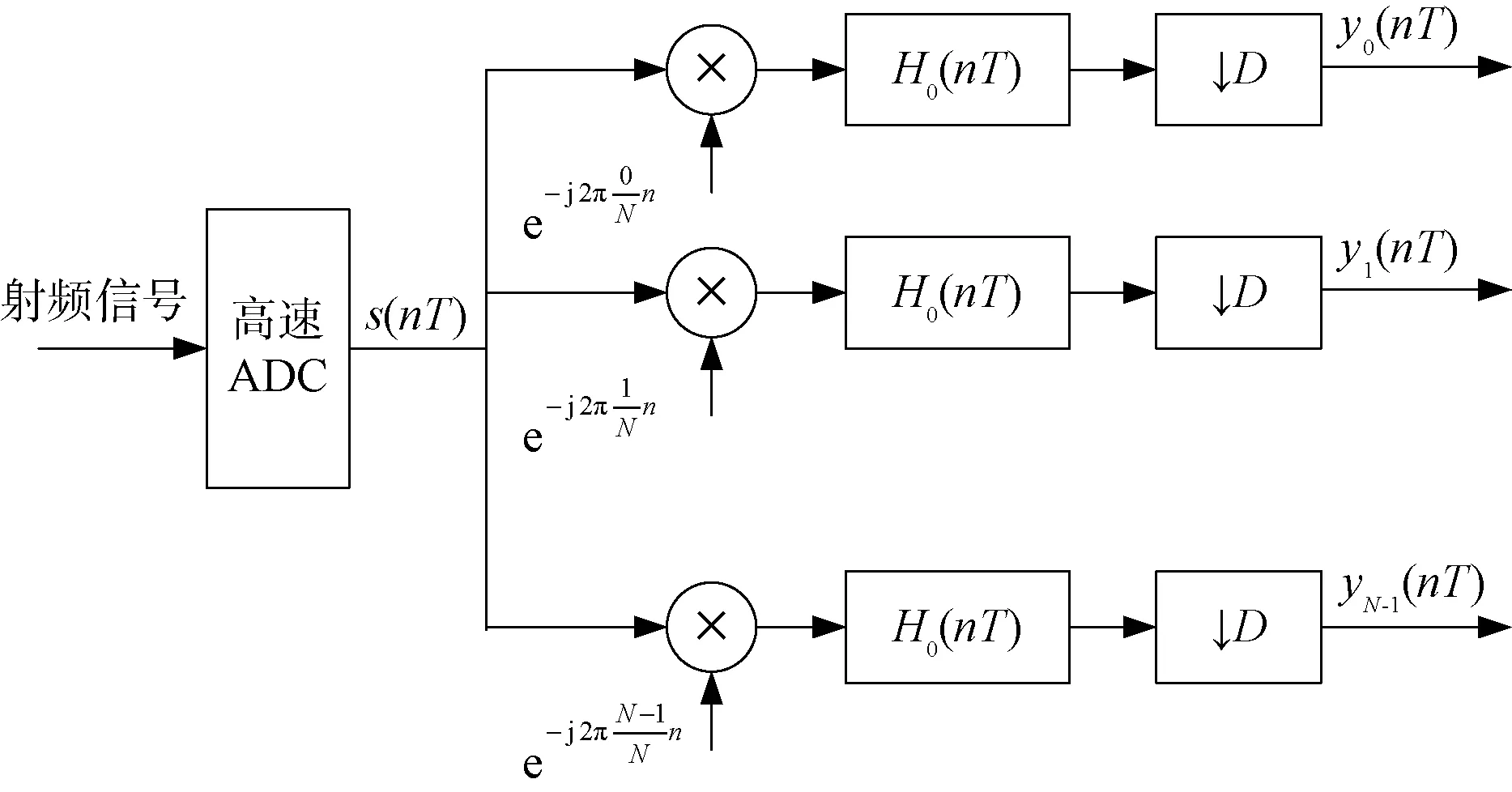
圖13 信道化接收機等效結構

這種結構的信道化接收機與上一種是完全等效的，只是每一個濾波器都是低通濾波器。如果信道寬度是均勻劃分的，那么每個信道的低通濾波器可以是一樣的，也就是說只需要設計1個低通濾波器，簡化了系統的設計。

但是，用圖12和圖13所示的濾波器組來實現信道化是很不經濟的，由于濾波運算位于抽取因子之前，對運算速度要求很高，對實時處理極其不利，尤其是當信道數多，抽取系數D值很大時，圖中的濾波器所需的階數可能會變得非常大，而且每一信道就要配一個這樣的濾波器，濾波后的數據大部分被抽取運算舍棄了，實現效率非常低，需要找到高效實現結構。

對于正交采樣系統，假設系統的采樣頻率為fs，整個系統的帶寬為fs，每個子帶帶寬為B，信道劃分為N份，抽取比D=N(N為偶數)，即：

fs=B·N

(9)

信道劃分形式如圖14所示。

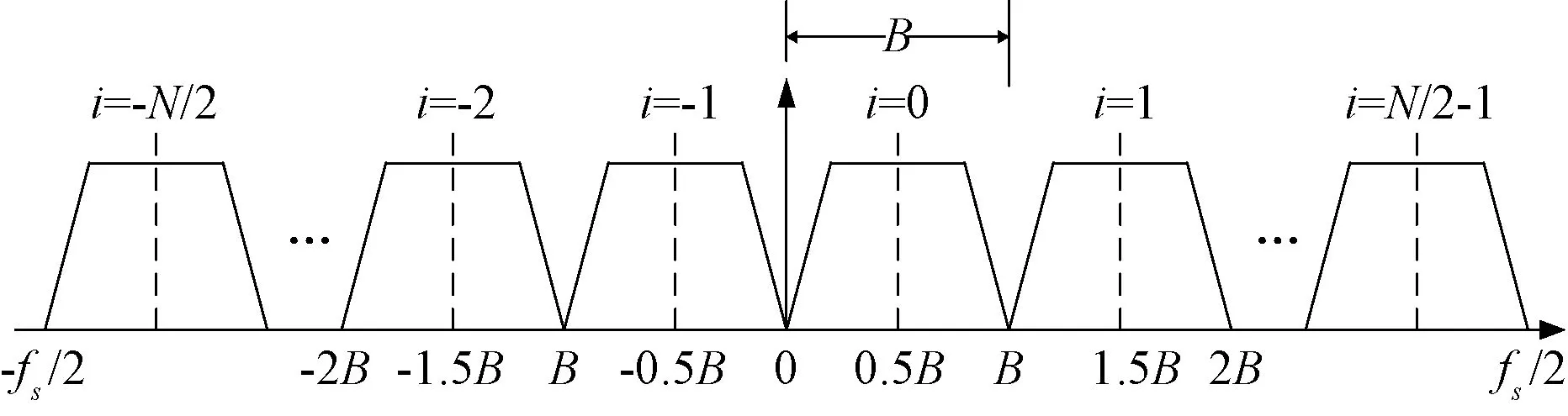
圖14 正交采樣系統下的信道劃分示意

下變頻時，取每個信道的中心頻率為本振頻率，即fo=i·B+B/2,i=-N/2,-N/2+1,…,0,1,2,…,N/2-1。

為了表示方便，一般取i～[0,N-1]，此時：

fo=(i-N/2)·B+B/2，i=0,1,2,…,N-1

(10)

則本振信號可以表示為：

(11)

當用數字方式產生本振信號時，t可以用nT來表示，T為采樣時間。得到第i個信道的數字化本振：

(12)

令低通濾波器的沖擊響應為h(t)，對于輸入信號為y(t)，經過傳統的數字下變頻后，信號可以表示為:

y(t)=[s(t)e-jωot]*h(t)=

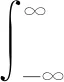
(13)

設采樣時間為T，經過離散化之后可以表示為：

(14)

用序列的形式來表達：

(15)

經過D點抽取后的信號可以表示為：

(16)

根據式(11),當抽取系數與信道數相同時，即D=N時，則:

(17)

則對于第i個信道，其輸出為：

i=0,1,2,…D-1，n=0,1,2,3…

(18)

利用多相濾波器的原理，將濾波器系數劃分為D部分(D與信道數一致)，每部分長度為M，M=ceil(K/D)，(不足部分作補零處理)，K=MD。即可以將k表示為如下的形式：k=m·D+L,L=0,…，D-1;m=0,…，M-1，將之代入式(18)，得到：

(19)

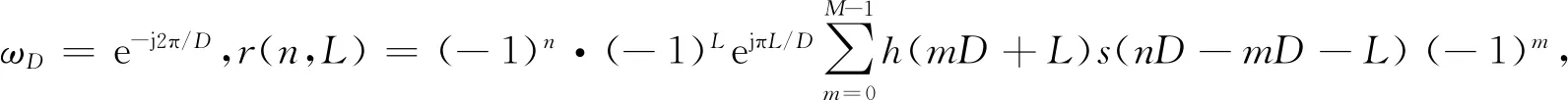
(20)

即第i信道的輸出為D個卷積結果r(n,L)進行離散傅里葉逆變換(IDFT)后的第i個頻率分量。

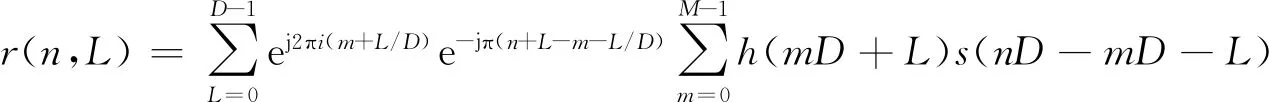
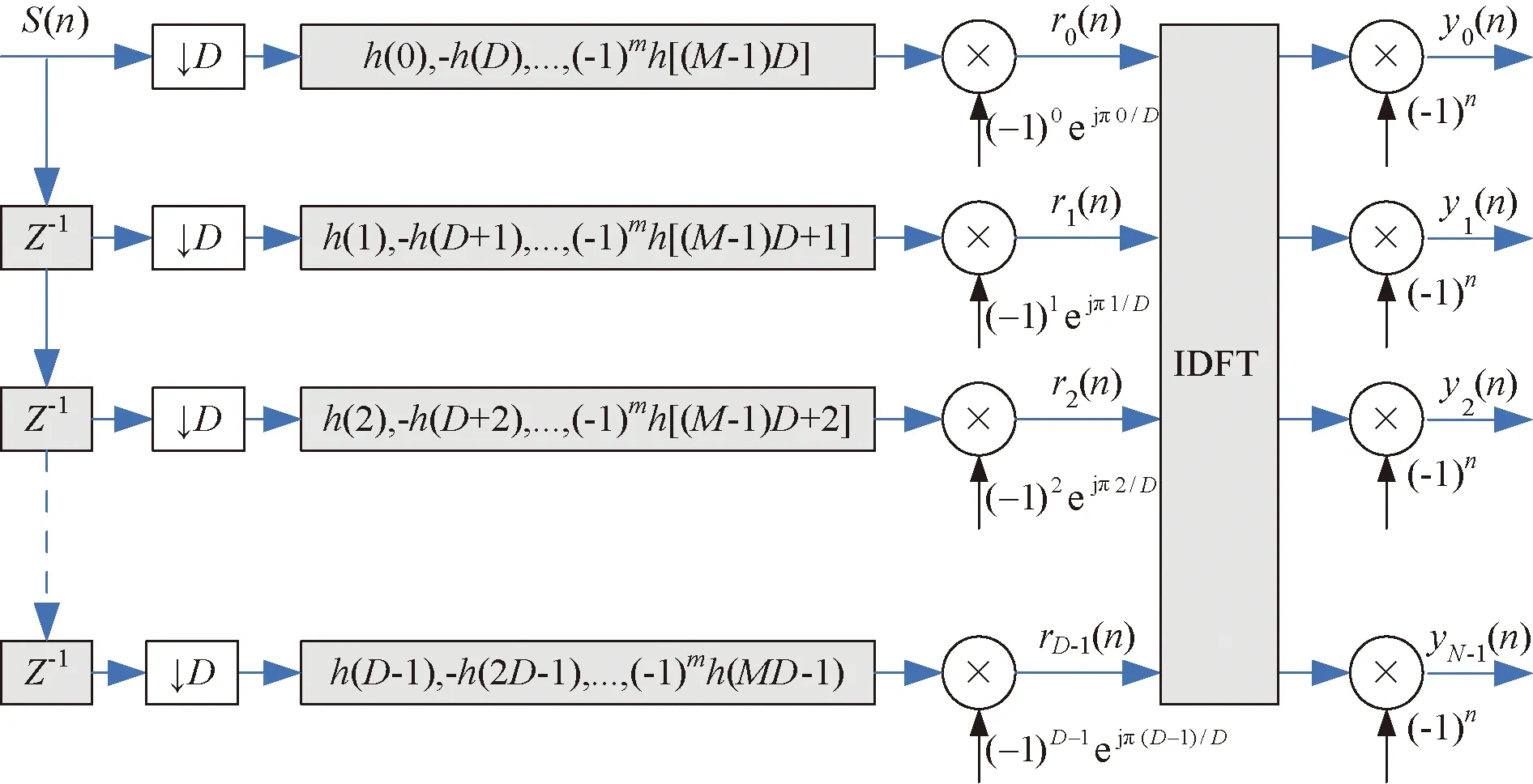
圖15 基于多相濾波器結構的數字信道化

對數字信道化的效能進行仿真驗證，以實際存在的多信號交疊場景為例，假設接收機到達的3個信號為：信號1：頻率-40 MHz的單頻信號；信號2：頻率30 MHz的單頻信號；信號3：中心頻率305 MHz，帶寬10 MHz的線性調頻信號。

3個信號在時間域重疊，在頻域位于不同頻率范圍。相對關系圖如圖16所示，同時到達信場景如圖17所示。

圖16 信號1，2，3相對時間關系圖

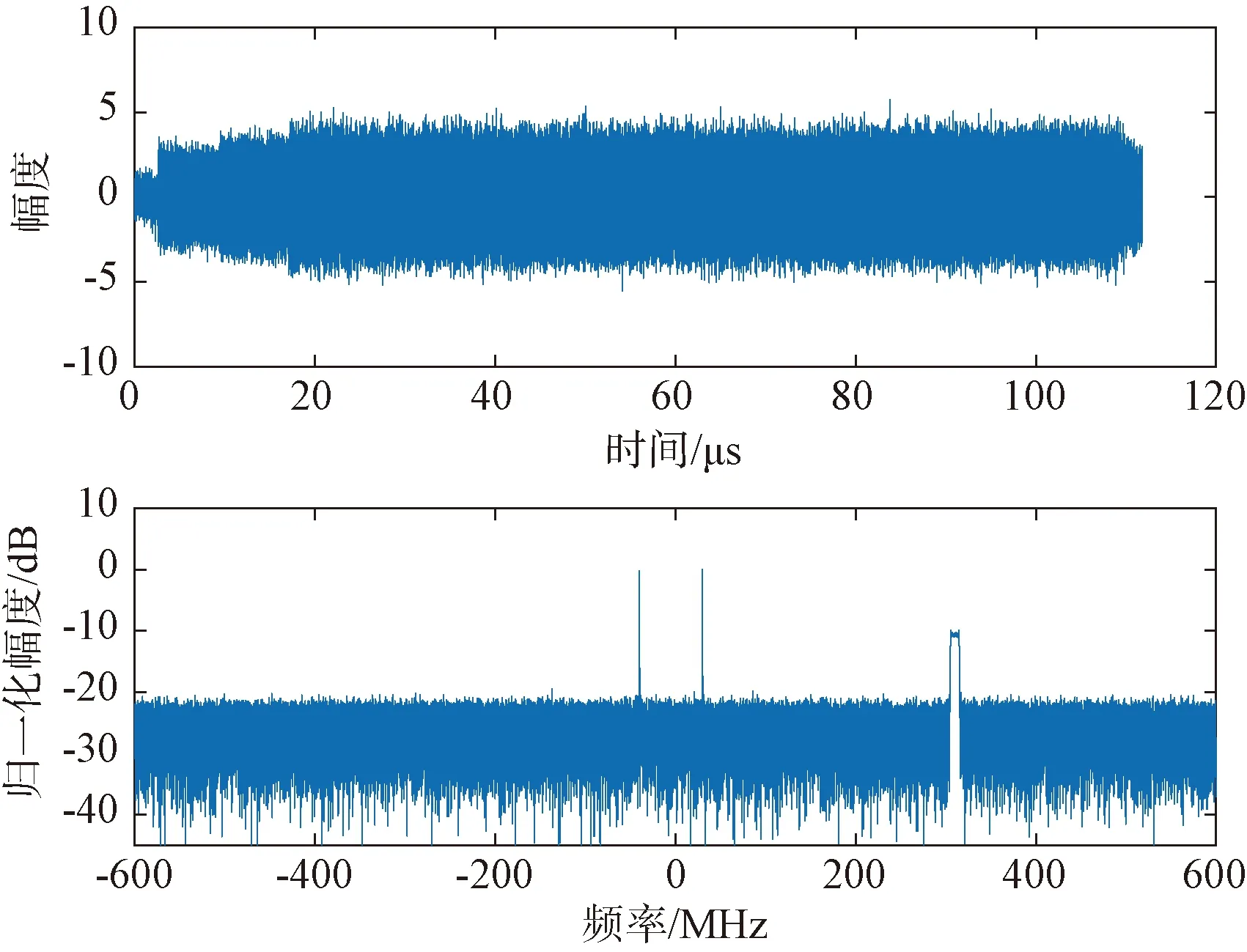
圖17 同時到達信號場景

進行64信道化信號的時域和頻域如圖18、圖19所示。有信號存在的信道如圖19所示。

圖18 64信道化處理后時域

未進行信道化處理前，3個信號時域重疊在一起，無法準確測量信號參數。信道化后能夠區分開，信道化細分后對同時到達信號的參數測量更準確，有利于后續信號分選和目標數據融合。

同時從圖19可以看出，信號3由于信道化的劃分導致信號被分割到2個信道，因此需要對信道17，18進行合并，在多信號到達時還需要進行通道融合處理，判斷跨信道信號和邊帶信號。這是下一個階段需要研究的內容。

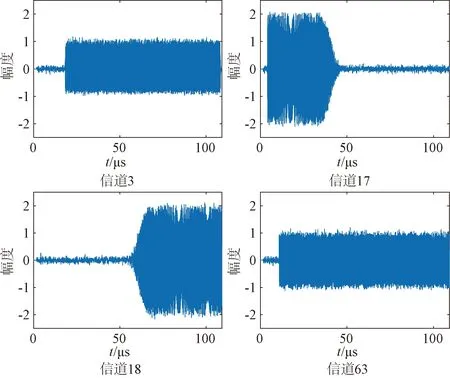
圖19 16信道3，17，18，63信道時域

6 展 望

目前的主流是將傳統的信道化接收的概念和寬帶數字接收機相結合起來的軟件化電子偵察接收機，將目前成熟的中頻數字處理技術應用于信道化接收機，用數字中頻信道化代替模擬濾波器組，克服傳統信道化接收機存在的問題和缺陷。這樣數字信道化接收機具有傳統模擬信道化接收機同樣的優點，又由于采用了數字技術，濾波器的一致性好、可靠性高，這不僅能夠大大提高測頻精度，而且符合數字化趨勢的發展潮流，整個接收機性能上將產生質的改變。

目前數字信道化主要應用在信號的偵察接收模型中，隨著FPGA器件的發展，在FPGA內實現發射信道化已經成為可能，將給雷達的抗干擾帶來更大的挑戰。