一種基于PCA-BP的直升機起落架著艦載荷評估方法

鄭甲宏，趙敬超

（中國飛行試驗研究院，陜西 西安 710089）

0 引 言

軍用直升機起落架研制在國軍標和型號規范中都有具體要求，如GJB 5771—2006《艦載直升機通用要求》中5.3.1描述“直升機起落架系統應充分吸收不小于3.05 m/s相對下沉速度著艦時的沖擊能量，不會發生永久變形，1.5倍的上述沖擊能量時，結構不會破壞”。因此直升機起落架在進行鑒定試飛考核時，必須測量著艦下沉速度達到飛行包線邊界的著艦載荷，考核起落架著艦載荷是否超過其結構的使用設計值，從而給出起落架鑒定試飛結論。

然而，研制的新型直升機起落架在進行大質量，大下沉速度，尤其是包線邊界及包線擴展工況下的著艦載荷飛行試驗時，起落架必然承受很大的著艦載荷。為了降低試飛風險，國內目前對于起落架著艦載荷的鑒定試飛并沒有考核到邊界狀態，而是采用起落架地面落震試驗來評估邊界狀態的著艦載荷。雖然落震試驗盡可能地模擬直升機在飛行試驗中的著艦工況，但是由于存在海上著艦環境、起落架與機體的約束、直升機著艦方式、著艦姿態等因素的差異，實際上地面落震試驗并不能取代飛行試驗。因此，準確地評估起落架的著艦載荷具有重大意義[1-2]。

研究人員嘗試采用建立數學模型的方法評估著艦載荷[3-6]。但是，由于模型涉及很多理論假設，且參數之間有很強的非線性關系，數學模型很難得出一個好的評估結果。目前很多研究通過建立神經網絡模型的方法來評估飛行載荷。美國海軍已經證明了通過飛行參數來評估結構載荷應變的可行性，并成功應用于F-14B的機體載荷應變評估。Cabell R H等[7]通過建立神經網絡模型，評估了AH-64A型直升機處于健康監控下的直升機關鍵飛行部件的交變載荷。在訓練過程和測試過程中，評估值和測量值有較高的相關性。

雖然通過建立神經網絡模型評估飛行載荷已經可以得到一個不錯的評估精度，但是有很多的參數影響直升機部件的載荷模型，而且這些參數之間有很強的相關性，如果將這些影響因素直接作為輸入變量應用于神經網絡模型，那么評估模型的結構將會非常復雜，容易使模型在訓練的過程中陷入局部最小值，通用性也會變得很差。本文采用主成分分析（PCA）與后退式神經網絡（BP）相結合的方法建立了評估模型，并對模型進行了驗證，取得了較好的效果，提高了直升機起落架著艦載荷的評估精度。

1 PCA-BP模型原理

1.1 PCA基本思想及求解

主成分分析采用一種降維的思想，通過產生幾個綜合變量，使它們包含盡可能多的原始變量信息，并通過這些選定的變量來解釋原始數據中的大部分變化[8-9]。

1）原始數據的標準化

通過下式對原始變量進行標準化：

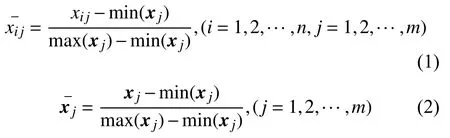
2）計算相關系數矩陣R

相關系數矩陣R可用下式計算：

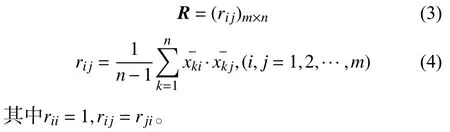
3）計算特征值和特征向量

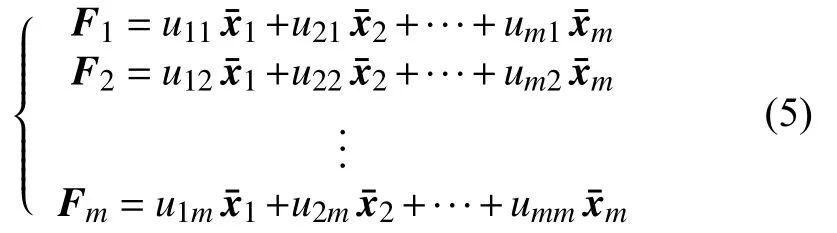
其中，Fm表示第m個主成分。

4）提取p個主成分

計算主成分的貢獻率和累積貢獻率，根據累積貢獻率提取p個主成分，直到特征值的累計貢獻率達到90%以上。通過下式可計算出第j個主成分的貢獻率bj與累計貢獻率ap：

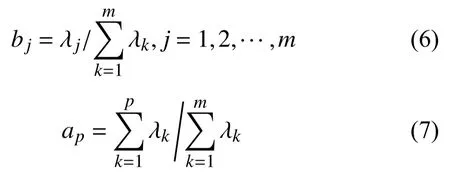
最后，原始樣本用p個主成分表示：

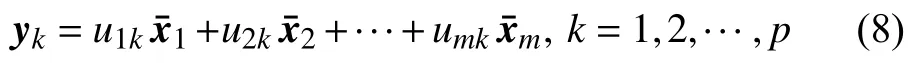
1.2 BP神經網絡原理

BP神經網絡已迅速發展成為一種重要的數學應用工具，成功解決了多個領域的評估問題。該方法具有強大的自學功能和非線性處理功能，可以不必確定自變量與因變量的函數關系，而是不斷地通過自身的學習訓練，達到求解復雜工程問題的目的，具有結構簡單，易于實現的功能的優點。

BP神經網絡結構如圖1所示，其中首尾兩層分別稱為輸入層和輸出層，中間各層稱為隱含層。BP神經網絡中各層之間的神經元為全連接關系，層內的各個神經元之間無連接。

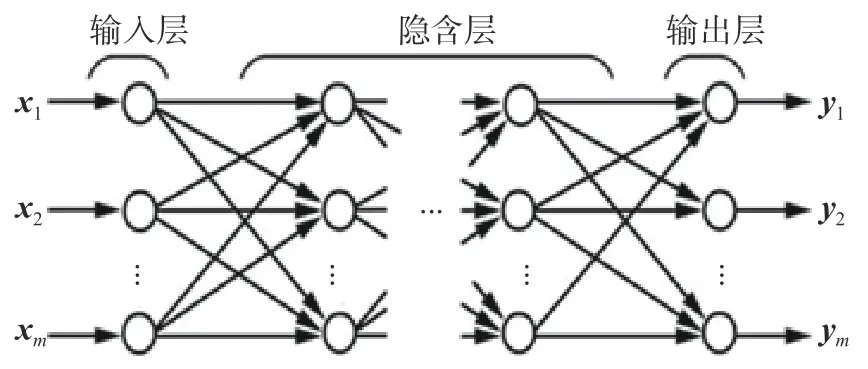
圖1 BP神經網絡的典型結構

BP神經網絡采用有指導的學習方式進行訓練和學習，即當一對學習模式提供給BP神經網絡后，神經元的激活值從輸入層經各個隱含層向輸出層傳播，在輸出層的各個神經元獲得網絡的實際輸出響應。通過比較輸出層各個神經元的實際輸出與期望輸出，獲得二者之間的誤差，然后按照誤差減少的方向，從輸出層經各個隱含層并逐層修正各個連接權值，最后回到輸入層。這種正向計算輸出-反向傳播誤差的過程不斷重復進行，直至誤差降低至可接受的范圍，BP神經網絡的學習訓練過程也就隨之結束。BP神經網絡求解評估問題的算法流程如圖2所示[10-11]。

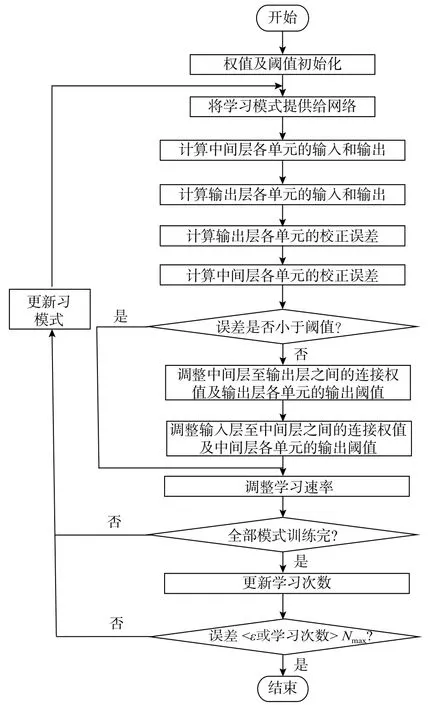
圖2 BP神經網絡算法流程

1.3 PCA-BP評估模型構建

將累積貢獻率達到90%的p個主成分作為BP神經網絡的輸入變量，并對神經網絡模型的參數進行調試，確定滿足精度要求的隱含層及其神經元的數量，最終得到PCA-BP模型。將模型的結構及參數保存，即可通過輸入變量得到評估值。PCA-BP評估模型流程如圖3所示。

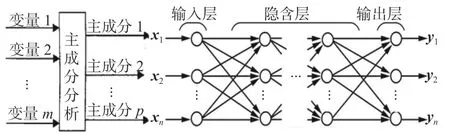
圖3 PCA-BP評估模型流程圖

2 試驗數據的獲取

直升機起落架在著艦狀態下，其輪軸主要受到垂向的彎矩和航向的剪切作用，搖臂受到彎矩和軸向力，防扭臂受到拉力和彎矩，內筒受到軸向力。為了測量其在著艦過程中的受載情況，在起落架上進行了應變計改裝，如圖4所示。通過開展地面載荷標定試驗，獲得了直升機起落架垂向載荷與起落架各部位應變的多元線性關系，即載荷標定方程。通過開展飛行試驗，采集直升機起落架著艦載荷過程中對應的著艦姿態、下沉速度、著艦質量重心、發動機參數等飛行狀態數據及起落架各部位著艦應變值，將應變值代入載荷標定方程，得到著艦垂向載荷。

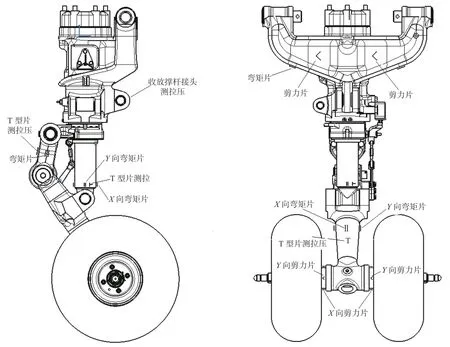
圖4 起落架應變貼片位置

3 起落架著艦評估模型的建立與驗證

將直升機的14個飛行狀態參數：無線電高度、飛行質量、下沉速度、法向過載、橫向操縱位移、縱向操縱位移、航向操縱位移、總距角、俯仰角、滾轉角、偏航角、俯仰角速率、滾轉角速率、偏航角速率進行主成分分析。這些參數可反映直升機起落架著艦時的飛行狀態，而且是直升機起落架著艦時主要的飛行監控參數。經主成分分析，每一個變量的方差和所有變量的累計方差如表1所示。一般認為參數的總累計方差達到80%～90%采用主成分分析是有效的。取前4個主成分，其總累計方差為89.786%，這4個主成分可以很好地表達14個飛行參數的內容。它們相互正交，相關系數為0，因而主成分分析達到了降低變量相關性的效果，而且減少了變量的個數，使模型簡單化。

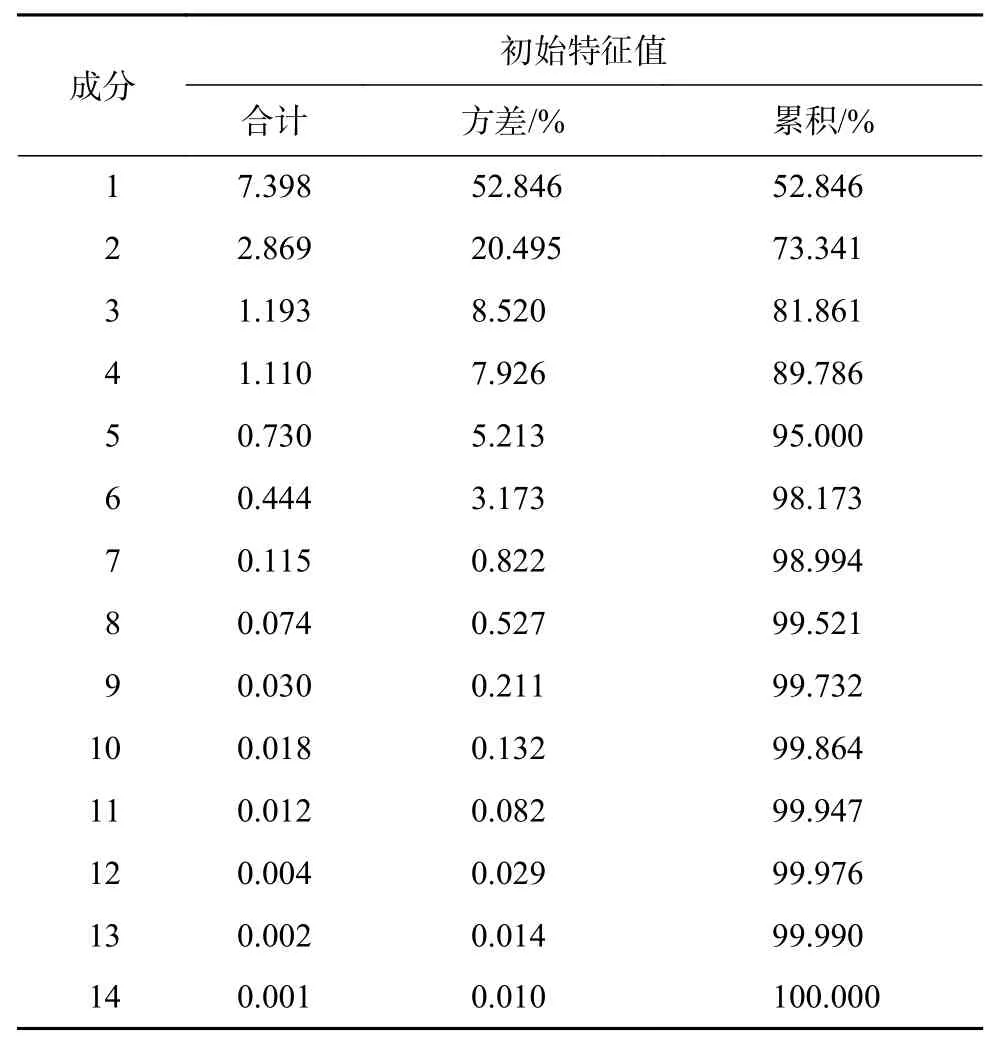
表1 解釋的總方差

把這4個主成分作為BP神經網絡的輸入量，起落架著艦載荷作為BP神經網絡的輸出量。由于模型的復雜程度一般，所以選擇只用一個隱含層的3層神經網絡結構，隱含層的轉移函數采用sigmoid函數，輸出層采用線性轉移函數，并采用Levenberg-Marquardt函數最優化算法來訓練神經網絡，目標誤差設定為0.01，學習效率設定為0.01。BP神經網絡的輸入層包含4個神經元，輸出層包含1個神經元。隱含層的神經元數目對整個模型的容錯能力具有重要的影響，其個數m可由經驗公式得出：

式中：A——輸出神經元數量；

B——輸入神經元數量；

C——1～10之間的常數[12]。

采用試湊法對不同隱含層神經元數目的網絡模型進行訓練，經過多次調試，當隱含層m=6時，其輸出誤差最小。從而BP神經網絡的模型結構為4×6×1。利用Matlab軟件進行建模及測試。模型數據分為訓練集和驗證集兩部分。其中訓練集占總樣本的比例為90%。采用均方根誤差RMSE和擬合優度r2作為旋翼槳葉揮舞載荷評估的誤差評價指標，其表達式為

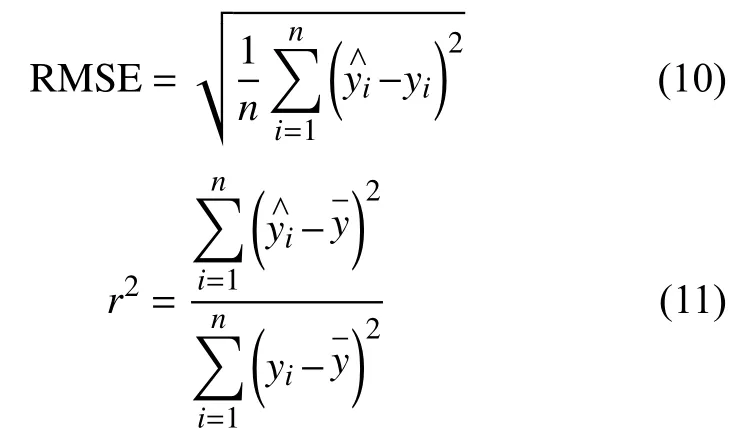
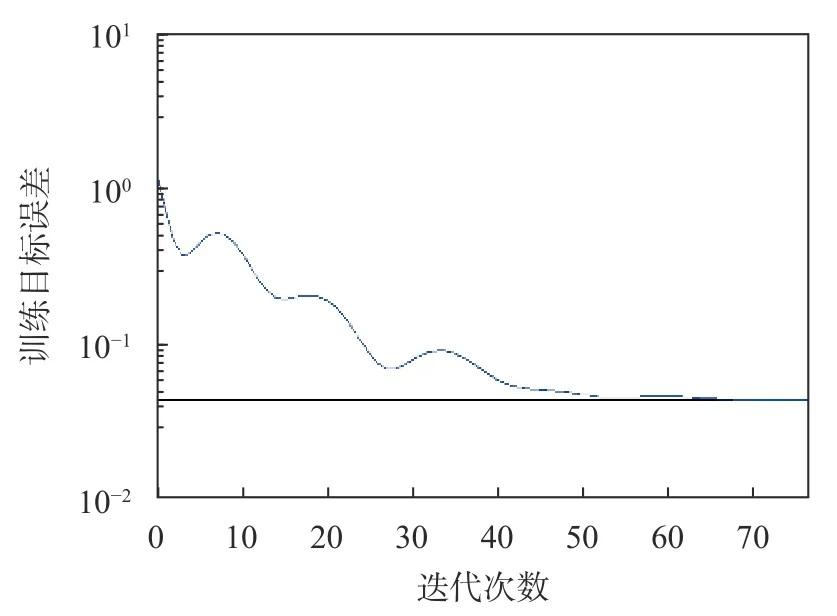
圖5 PCA-BP模型訓練樣本誤差輸出曲線

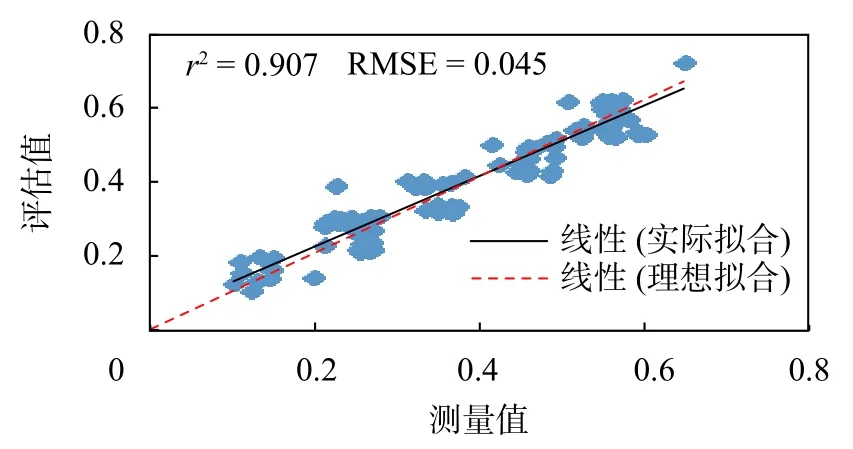
圖6 PCA-BP模型驗證樣本評估值與測量值對比

為了進行模型的對比分析，在BP神經網絡訓練中，把14個飛行狀態參數直接作為輸入變量，起落架載荷作為輸出變量，進行全要素的BP神經網絡訓練，模型的訓練數據、驗證數據及模型參數的選取方法同PCA-BP模型。全要素BP神經網絡的訓練樣本的誤差輸出曲線如圖7所示，驗證數據的輸出結果如圖8所示。

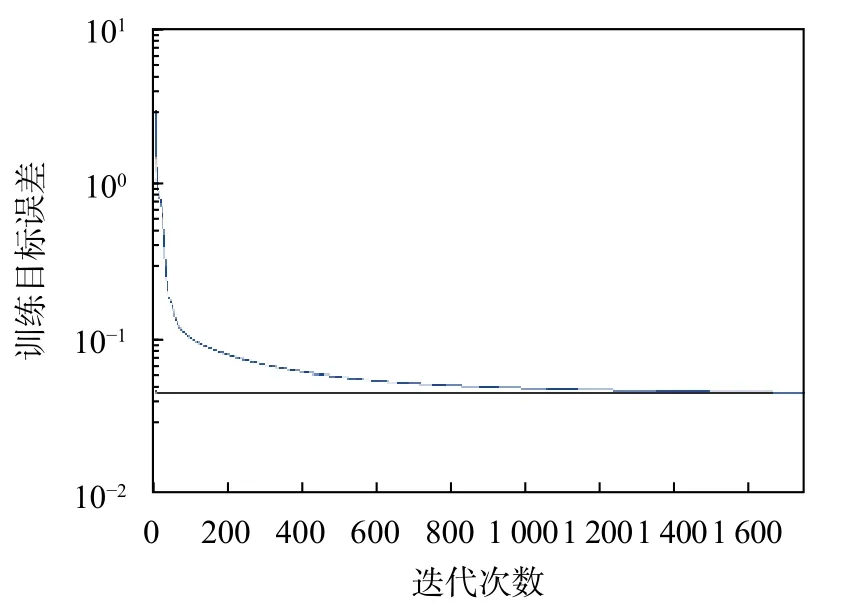
圖7 BP模型訓練樣本誤差輸出曲線

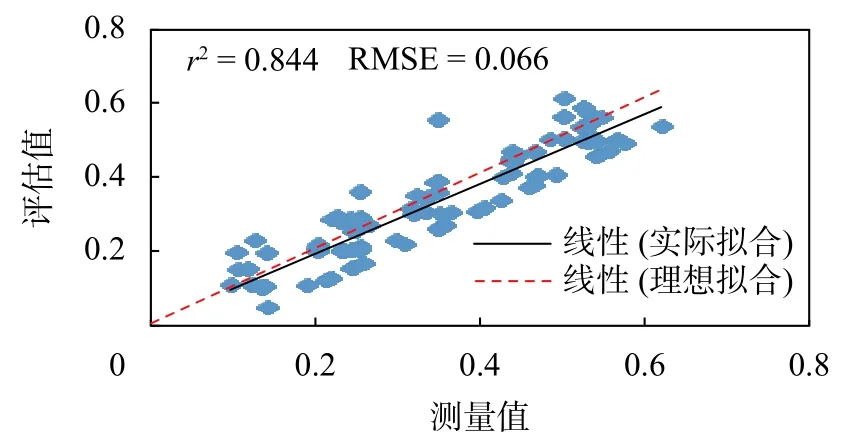
圖8 BP模型驗證樣本評估值與測量值對比

從圖5和圖7模型訓練樣本的誤差輸出曲線可以得出，欲達到同一期望誤差精度0.045，BP神經網絡模型需要訓練1 623步，而基于PCA-BP模型只需要67步。可見，PCA-BP模型具有更快的收斂速度。從圖6和圖8可以得出，BP神經網絡模型的擬合優度r2為0.844，均方根誤差RMSE為0.066，而PCA-BP模型其擬合優度r2為0.907，均方根誤差RMSE為0.045。可見，PCA-BP模型具有更高的精度。

4 結束語

本文提出將主成分分析和BP神經網絡相結合進行直升機起落架著艦載荷的評估，對影響著艦載荷的飛行狀態參數進行了主成分分析，其結果作為BP神經網絡的輸入數據，克服了自變量間的多重共線性問題，減少了輸入變量的個數。結果表明，PCA-BP模型相比于全要素BP神經網絡模型精度更高，收斂速度更快。