電場傳感器性能改善算法研究

韓 文，吳 健，程珍珍，唐露甜，孫利利，章 凱，張 勇

（1.國網陜西省電力公司電力科學研究院，陜西 西安710199; 2.西安交通大學，陜西 西安710049）

0 引 言

隨著電力系統的高速發展，高壓（特高壓）輸電線路日益增多，因靜電效應、磁場效應及電暈現象引起的一系列“環境影響問題”對公眾生產生活的影響日益突出[1-2]。現實中，輸電線路電磁環境會隨著電壓、電流以及天氣原因等眾多因素的影響而產生變化，需要進行長期觀測統計其規律[3-5]。獲取我國輸變電工程電磁環境的基本參數，掌握其規律，對指導今后的輸變電線路設計和建設具有重要意義；電磁環境監測數據將為我國建設以特高壓為骨干網架的堅強智能、綠色、環保電網提供有力的技術支持。針對工頻電場，目前主要采用傳統的電學式電場傳感器[6-9]和光學式電場傳感器[10-12]進行檢測，能用于實際環境中的電場傳感器產品大多來自于國外，國內產品尚處于實驗研制階段，在現場環境下檢測誤差較大，抗干擾能力差，難以滿足實際中的工程需要。

傳統的電場傳感器存在機械結構復雜、量程窄、溫漂大等缺點。為了改善傳感器的檢測性能，一部分學者[12-14]試圖通過改變傳感器的結構來改善其性能，如凌碧云等[8]提出了一種諧振式的三維電場傳感器，測量范圍為0～120 kV，但其交叉靈敏度和測量誤差相對較高，分別為5.48%和6.16%，且諧振式的電場傳感器諧振頻率不易控制。一旦傳感器的結構確定，該方法耗費時間和資金成本較大。因此，另外一些方法則是從算法的角度出發，利用機器學習算法改進傳感器的性能。李冰等[13]提出了一種基于遺傳算法的三維電場傳感器解耦標定方法，使合成電場的相對誤差從4.4%減小到了1.9%，但該方法存在易丟失最優解的缺點。聞小龍等[14]通過求逆矩陣運算的方法獲得傳感器的耦合靈敏度矩陣，完成了對其設計的三維電場傳感器的標定，最大相對誤差為10.2%，未能有效地改善傳感器的性能，當計算過程中矩陣奇異或接近奇異時，計算復雜耗時且存在計算誤差。

為了進一步提升電場傳感器的檢測性能，提高電場傳感器在檢測工頻電場的準確度，本文采用國產森馥SEM-600低頻電磁輻射測量儀對一臺標準工頻電場發生器中心區域產生的0～20 kV/m三維電場進行了測量，首先使用最小二乘法評價了該傳感器的靜態特性指標，得出其誤差為13.6%，分析認為，影響其指標性能較低的可能原因為交叉靈敏度。利用機器學習的方法，分別采用BP神經網絡、徑向基神經網絡、支持向量機和遺傳算法等算法，對檢測數據進行對比分析，得到了優化后的三維電場值，并消除了三維電場之間的交叉干擾，傳感器準確度得到較大改善。

1 電場信息獲取

標準工頻電場發生器實物如圖1所示，采用圓形平行極板，極板半徑為800 mm，間距為1 200 mm，距地高度為1 000 mm，裝配12個半徑為800 mm、管徑為50 mm 的均壓環。在95%置信概率下，標準工頻電場發生器的擴展不確定度為0.7 %。

圖1 標準工頻電場發生器實物圖

本文采用國產森馥SEM-600低頻電磁輻射分析儀對工頻標準電場發生器中心區域的工頻電場強度進行了測量。以電場發生器的中心為原點建立了三維空間坐標系，軸向為z軸，徑向是xoy平面（左手系）。傳感探頭放置于工頻標準電場發生器兩極板的正中心，如圖2所示。啟動標準電場發生器產生標準電場，國產森馥SEM-600三個正交電場傳感器在圖2中對標準電場產生響應，工頻標準電場變化范圍為0～20 kV/m。在標準電場發生器產生的工頻電場方向不變的前提下，旋轉傳感探頭，分別使三維傳感探頭處于圖2中定義的3種不同姿態，從而分析傳感器的交叉敏感系數。 姿態1、2、3分別將傳感器的z、x、y軸與電場發生器的z軸平行放置。

圖2 森馥SEM-600電場傳感器測量過程示意圖

2 三維電場提取

2.1 三維電場分解

將電場矢量E分解為x、y、z 3個互相垂直方向上的電場分量（圖3），即

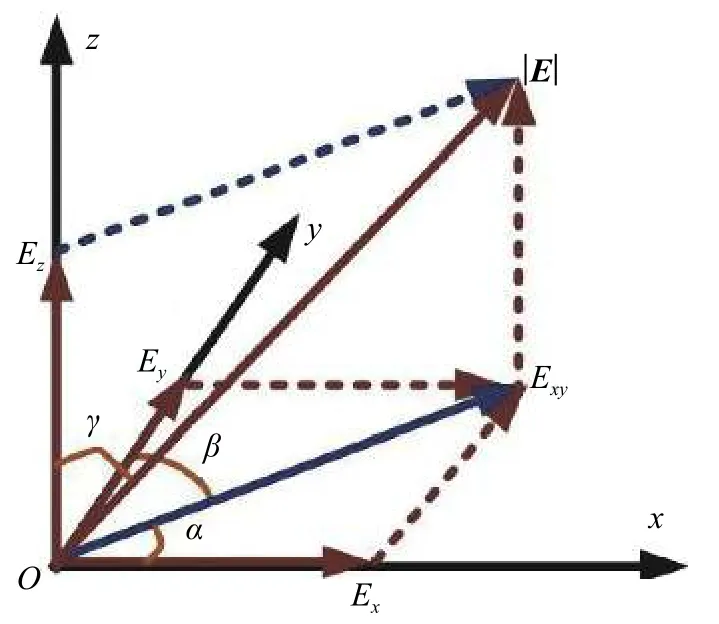
圖3 三維電場分解原理圖

因此，只要測得電場在空間x、y、z 3個方向上的3個分量，就可得到被測電場強度E：

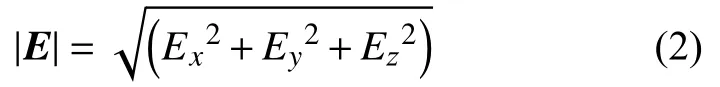
其中|E|為電場的模值。

2.2 三維工頻電場檢測結果

本文對Ex、Ey、Ez每個方向進行5組正反行程的實驗，共獲得了15組三維電場值數據。另外，為了驗證算法的效果，還額外進行了3組正反行程的實驗。圖4（a）～圖4（c）分別為傳感器z軸向上時對電場發生器產生的工頻電場矢量E在x、y、z3個方向上的分量值的響應Ex、Ey、Ez，可以看出，Ez的值最大，與標定電場大小及方向保持一致；電場模值|E|可由公式（2）計算得到。表1為姿態1正行程采集數據。

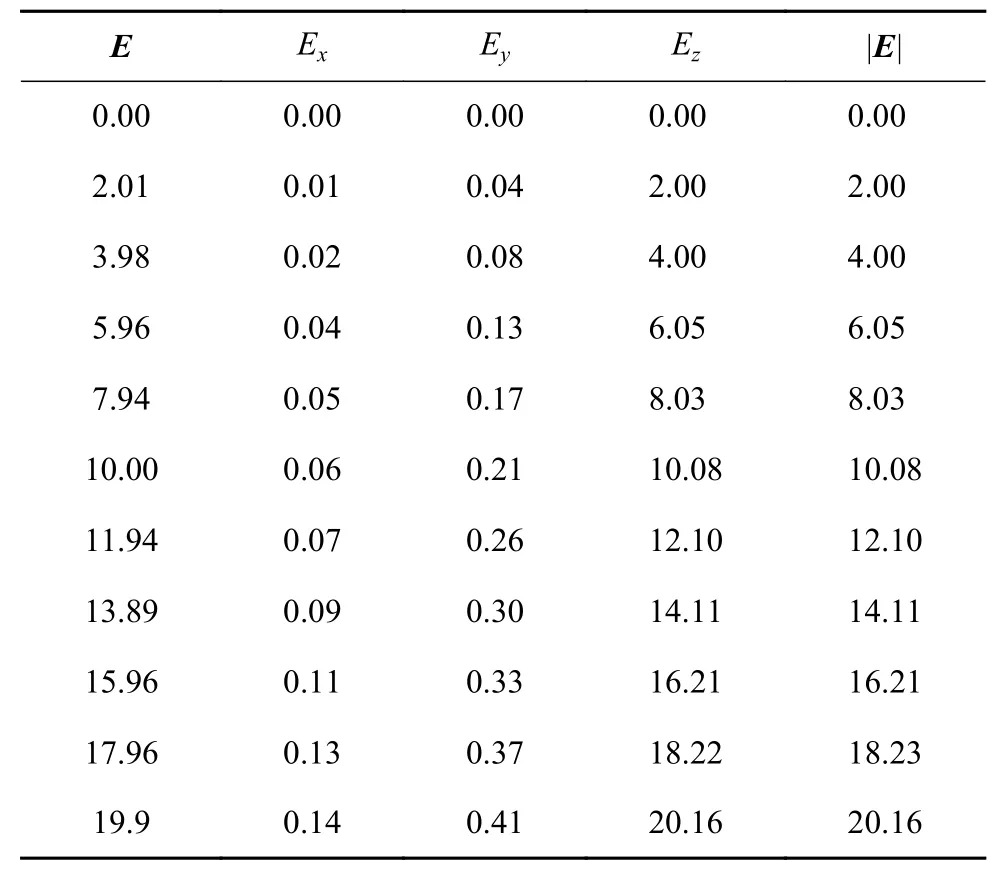
表1 傳感器處于姿態1時三維電場檢測結果（部分） kV/m

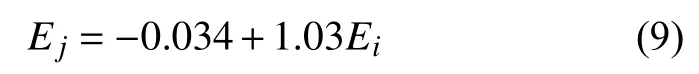
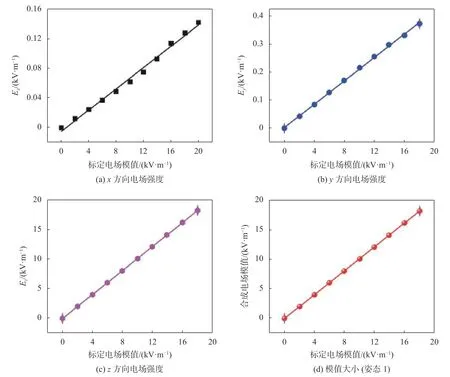
圖4 各方向電場強度及模值大小（姿態1）

2.3 傳感器靜態性能指標計算

為了評價該傳感器的性能，依據國家標準GB/T 18459—2001 《傳感器主要靜態性能指標計算方法》，首先采用了最小二乘法對其準確度指標進行計算，主要包括線性度、遲滯、重復性。

由實驗數據進行實驗建模，采用下式表示傳感器的靜態模型，即求取多項式的各項系數：

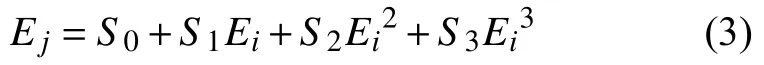
當采取簡化的直線方程來表示靜態模型時，則只需求取擬合直線的零位與靈敏度兩項系數。

設擬合直線方程通式為

則第i個標定點的標定值Ei與擬合直線上相應值的偏差為

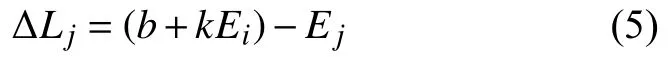
最小二乘擬合直線的擬合原則是使N個標定點的均方差為最小值：

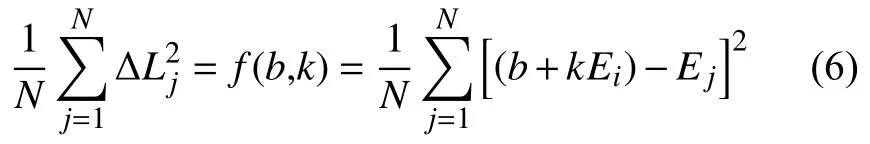
由一階偏導等于零，即

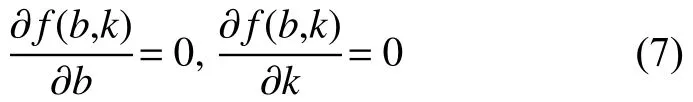
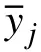
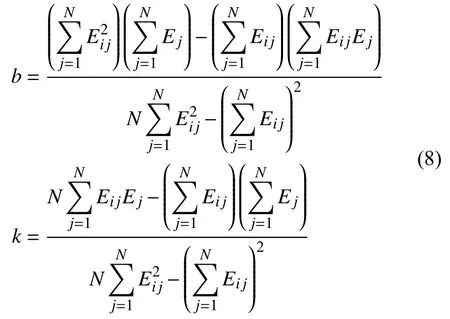
故最后計算得最小二乘擬合直線方程為

該電場傳感器場強測量結果Ej與被測電場模值Ei之間的靜態模型。

1）線性度δL

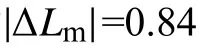
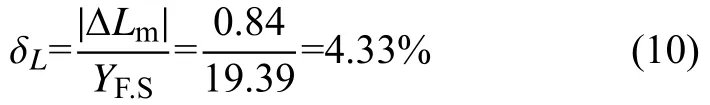
2）計算遲滯δH

先計算各標定點的滯后差=正行程（平均值）-反行程（平均值），選取其中的最大值為|ΔHm|=0.17（kV/m），則有：

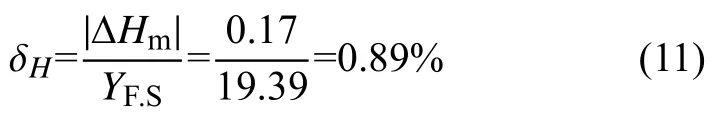
3）計算重復性δR

重復性用引用誤差形式表示為:

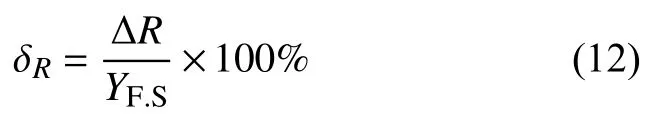
其中ΔR為同一輸入量對應多次循環的同向行程輸出量的分散程度。計算可得最小二乘的重復性為8.41%。

4）計算誤差A

A由線性度ΔL、遲滯ΔH與重復性ΔR的絕對值求和得出：

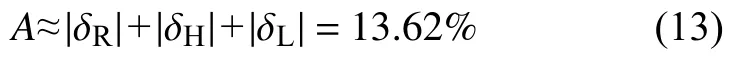
根據擬合直線方程 （5）計算各標定點的擬合值E′d、最大擬合偏差|ΔLm|、最大遲滯偏差|ΔHm|以及重復性偏差ΔR，計算線性度ΔL、遲滯ΔH、重復性ΔR及誤差A這4個性能指標，結果見表2。

表2 傳感器基本質量指標

可以看出，當采用傳統的最小二乘方法計算該電場傳感器的靜態指標，傳感器的準確度較大，很有可能是因為電場三維分量的檢測存在交叉干擾，導致傳感器性能降低。因此，還需要對傳感器的交叉靈敏度做分析。

2.4 電場三維分量的交叉敏感

交叉靈敏度系數αm-n（表3）用于評價非目標參量En對被測目標參量Em的影響程度，計算式如下：

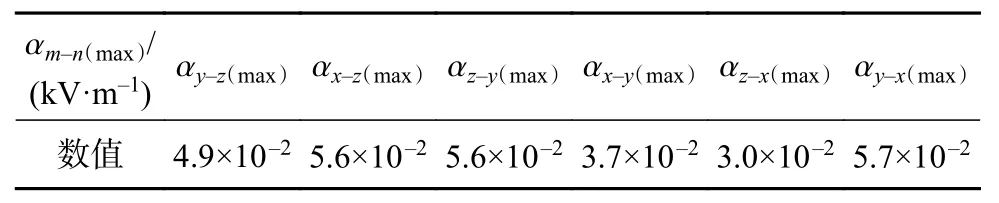
表3 最大交叉敏感系數αm-n（max）

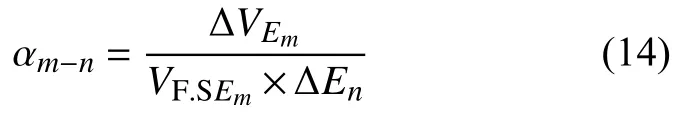
式中：m,n=x,y,z且m≠n；

ΔEn——非目標方向電場變化量；

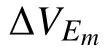
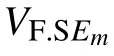
表3說明三維電場分量之間都存在著交叉干擾，x方向電場分量Ex對分量Ey交叉干擾最大。交叉干擾的存在，無疑會降低傳感器檢測結果的準確度。因此，建立基于神經網絡、支持向量機等智能算法消除交叉干擾，以提高電場傳感器的性能。

3 傳感器性能分析及改善

正如2.3節的分析，現場測量電場用的森馥SEM-600三維電場間存在著交叉干擾的影響，因此采用機器學習的方法，消除交叉干擾，提高電場傳感器的性能。通過對比4種智能算法對性能改善的效果，選出最優方法。

3.1 基于BP神經網絡的傳感器讀數模型建立

研究采用BP神經網絡融合方法減小方程（5）的擬合誤差。構建3個輸入神經元節點、7個隱層神經元節點、4個輸出神經元節點的BP神經網絡（BPNN）（圖4），電場三維分量的檢測結果 Ex、Ey、Ez作神經網絡的3個輸入，電場強度的模值|E|和E′x、E′y、E′z為神經網絡的4個輸出。

3.1.1 BP神經網絡樣本文件的建立

在電場發生器的中心位置，三維電場傳感器對0～20 kV/m量程（步長為2 kV/m）的工頻電場進行了5個正反行程的檢測，獲得了360組樣本數據，即x、y、z 3個方向共有360組樣本數據。在電場量程范圍內抽取了300組數據作為訓練樣本，用于建立神經網絡讀數模型；剩下的60組數據作為檢驗樣本，用于檢驗神經網絡的讀數結果是否達到期望的誤差要求。

3.1.2 網絡結構參數的確定

基于Matlab軟件的newff函數建立神經網絡訓練模型，圖5輸入層采用purelin純線性函數，輸出等于輸入；隱層傳遞函數采用logsig函數，對輸入層的輸出加權后進行歸一化處理，去除白噪聲；輸出層采用purelin純線性函數，將隱層輸出量加權求和后輸出。當輸出層的輸出結果誤差滿足對誤差的期望要求時，訓練結束。然后，用函數net.IW、net.LW分別獲取輸入層和隱層間的權值wij，及隱層和輸出層間的權值vjk；用net.b分別獲取隱層和輸出層的閾值bj、ck；從而確定神經網絡的結構參數。

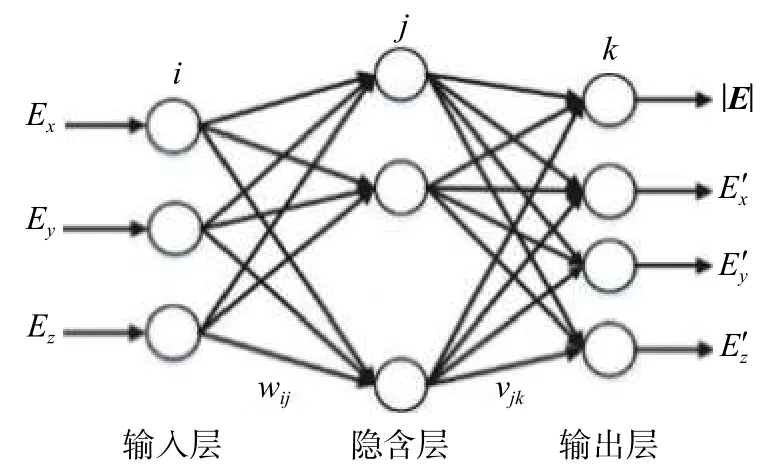
圖5 神經網絡讀數模型結構圖

①輸入層

輸入層節點i的輸出為：

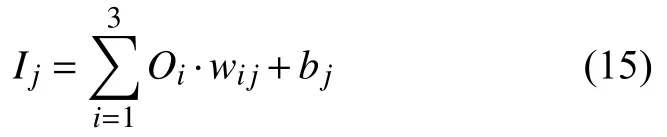
式中：wij——隱層第j個隱層節點與第i個輸入節點的連接權值，j=1,2,···,7；

bj——第j個隱層節點的閾值。

節點j的輸出為：

②輸出層

第k個節點的總輸入為：

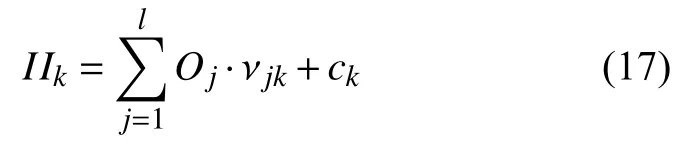
式中：ck——第k個輸出節點的閾值；

vjk——隱層第j個隱層節點與第k個輸出節點的連接權值。

節點k的輸出為：

式中：y1——|E|；

y2、y3、y4——E′x、E′y、E′z。

3.1.3 BP神經網絡讀數模型性能檢驗

神經網絡讀數模型能否實用，需要用檢驗樣本驗證，檢驗樣本誤差達標即驗證合格后，獲得BP神經網絡的結構參數wij、vjk、bj、ck（表4）。

將檢驗樣本數據和表4數據代入式（15）～（18）后，得到被測電場Ei的檢驗結果E′i。基于最小二乘法擬合獲得兩個參量的關系式：

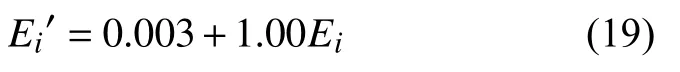
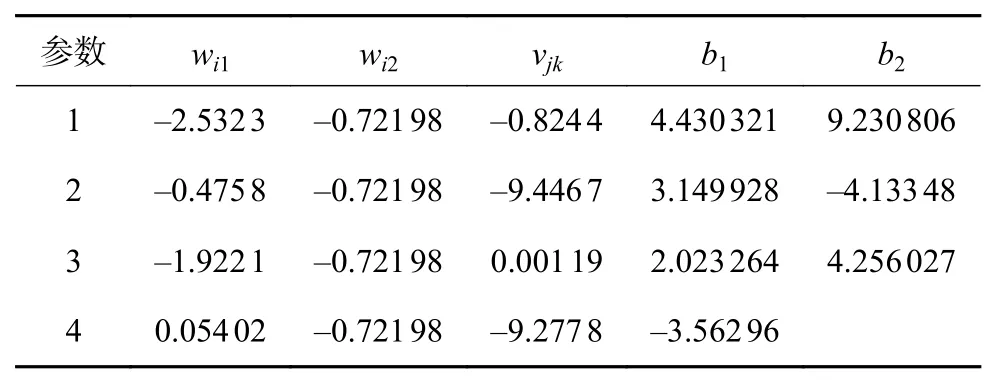
表4 BP神經網絡權值、閾值表

根據式（10）～（13）計算了線性度、遲滯、重復性和誤差（表5）。表2與表5數據的對比說明，經BP神經網絡融合后，傳感器的指標（線性度、重復性、遲滯和誤差）較基于最小二乘法融合后的傳感器指標都有一定程度的改善。相對于最小二乘法而言，BP神經網絡是基于誤差逆向傳播的算法，理論上通過不斷迭代，可以實現誤差的最小，這也是經BP神經網絡融合后，傳感器性能指標提高的原因。

表5 基于BP神經網絡模型的傳感器性能指標

3.2 基于支持向量機的傳感器讀數模型

從3.1節中可以看到，經過BP神經網絡建模后，傳感器的相關指標有了一定提升，但是效果并不明顯。BP神經網絡建立的讀數模型的性能取決于標定數據的數量，數量越多，融合結果誤差越小；而在實際應用過程中所獲得的標定數據（樣本）數量往往是有限的，導致誤差增大。為解決有限樣本的訓練問題，這里采用小樣本學習機理的支持向量機技術建立傳感器的讀數模型。

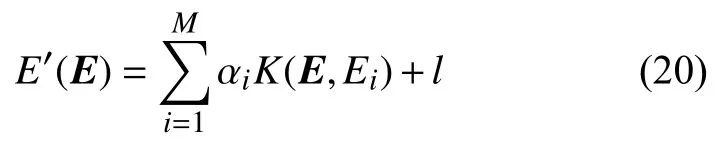
圖6 支持向量機模型

這里采用徑向基核函數：

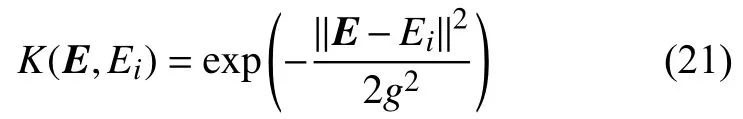
其中g為核函數參數，且g＞0。

徑向基核函數作為支持向量機的核函數，只需調節懲罰因子C和核函數參數g兩個相關參數，就能得到理想的分類準確率。

采用粒子群優化，經迭代計算得懲罰因子C和核函數g的最優解，C=1.36×105，g=32.59。

基于最小二乘法擬合兩個參量的關系式：

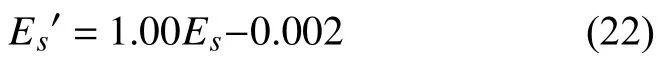
根據式（10）～（13）計算了支持向量機讀數結果的線性度、遲滯、重復性和誤差（表6）。

表6 基于支持向量機模型的傳感器性能指標

經支持向量機融合后，傳感器的遲滯和重復性指標比原始數據計算得到的指標及BP算法改善后的指標有較大程度的改善，誤差由原始讀數模型的減小到了1.9 %。可見，采用小樣本學習機理的支持向量機技術，可以建立更為準確的傳感器讀數模型。

3.3 與其他讀數模型結果的對比

為了與其他智能算法的效果進行對比，優化電場傳感器的檢測指標，本文還采用了徑向基神經網絡和遺傳神經網絡來優化傳感器的性能。5種不同方法的誤差對比（表7）對比說明，在有限的樣本條件下，基于支持向量機的數據融合方法更有效地改善了傳感器的性能，消除了電場三維方向的交叉干擾，減少了測量誤差。

表7 使用不同建模算法數據融合后傳感器誤差的對比

本文所用森馥SEM-600低頻電磁輻射測量儀輸出數據經數據融合后，測量儀線性度及誤差指標均優于現有技術（表8），在電場檢測領域具有顯著優勢。

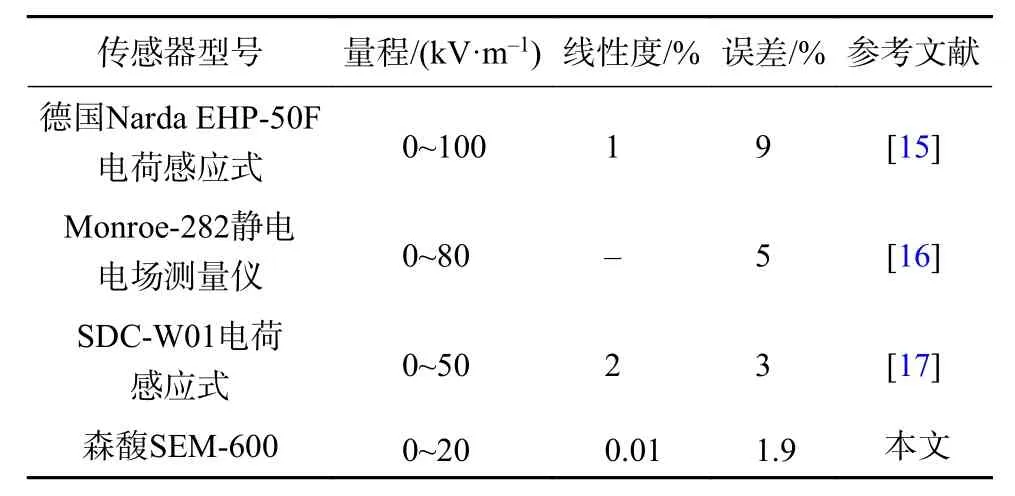
表8 與現有電場傳感器性能指標對比

4 結束語

在一個標準電場發生器中對SEM-600三維電場傳感器進行了標定。采用最小二乘法對三維電場的檢測結果進行了分析，獲得傳感器的誤差為13.6%。檢測結果表明，三維電場檢測存在交叉干擾。為了消除交叉干擾，提高檢測準確度，采用了神經網絡、支持向量機等智能算法，對傳感器的性能進行了優化。5種方法讀數結果的對比表明，在相同的樣本數量下，基于支持向量機的讀數模型，使電場傳感器的線性度和重復性分別從原始數據的4.33%和8.41%，顯著提高至0.01%和1.05%，誤差從原始數據的13.6%降低至1.9 %，極大減少了傳感器的檢測誤差。