無人直升機(jī)吊掛運(yùn)輸飛行協(xié)調(diào)控制設(shè)計(jì)
藍(lán)啟城,賴水清
(1.中國船舶工業(yè)系統(tǒng)工程研究院,北京 100094;2.中國直升機(jī)設(shè)計(jì)研究所,江西 景德鎮(zhèn) 333001)
0 引言
直升機(jī)吊掛飛行的動(dòng)力學(xué)問題在20世紀(jì)60年代末開始受到廣泛關(guān)注。最早的記載是1965年由Lucassen和Sterk所發(fā)表的文獻(xiàn),提出了一種垂直面內(nèi)3自由度模型,采用單點(diǎn)吊掛假設(shè)并忽略了作用在吊掛物上的氣動(dòng)力和力矩。分析結(jié)果指出吊掛物擺動(dòng)運(yùn)動(dòng)模態(tài)是穩(wěn)定的,直升機(jī)長周期模態(tài)仍不穩(wěn)定,并且其頻率隨吊索長度增加而降低。Szustak和Jenney指出,傳統(tǒng)的直升機(jī)增穩(wěn)系統(tǒng)在吊掛懸停和釋放吊掛物過程中顯得不足,可能會(huì)導(dǎo)致駕駛員誘發(fā)震蕩現(xiàn)象。后來,Dukes采用了和Lucassen相同的簡化方法,在頻域里研究了直升機(jī)吊掛飛行的穩(wěn)定性,并為吊掛飛行設(shè)計(jì)了可能行之有效的增穩(wěn)措施和適宜的操縱手段,在理論上證明了在反饋機(jī)制中包含吊點(diǎn)的縱向移動(dòng)會(huì)增強(qiáng)吊掛飛行的穩(wěn)定性,但并未試驗(yàn)驗(yàn)證。以上研究局限于懸停和低速飛行狀況,此時(shí)吊掛物的氣動(dòng)特性影響比較微小。Poli和Comack研究了吊掛物分別為2.44m×2.44m×6.1m的集裝箱和底面直徑為1.65m、長6.1m的圓柱體的前飛穩(wěn)定性,研究中考慮了吊掛物的氣動(dòng)特性,得出長吊索、大速度和輕載荷能提高吊掛物的穩(wěn)定性的結(jié)論。
隨著現(xiàn)代傳感器和控制技術(shù)的發(fā)展,尤其是差分GPS(全球定位系統(tǒng)),激光雷達(dá)(光探測和測距),全權(quán)限飛行控制系統(tǒng),直升機(jī)主動(dòng)飛行控制技術(shù)等的發(fā)展,直升機(jī)系統(tǒng)的狀態(tài)感知和航跡精確控制能力顯著提高,為新型直升機(jī)協(xié)調(diào)吊掛方式的實(shí)現(xiàn)鋪平了道路。
國內(nèi)相關(guān)直升機(jī)外吊掛飛行的研究集中于兩所高校,且起步較晚。最早的文獻(xiàn)發(fā)表于2004年。南京航空航天大學(xué)的研究主要集中在重型直升機(jī)外吊掛飛行的研究。北京航空航天大學(xué)主要研究重型直升機(jī)在增穩(wěn)控制系統(tǒng)工作條件下外掛載荷運(yùn)輸飛行任務(wù)中的飛行品質(zhì)問題。
綜觀國內(nèi)外研究現(xiàn)狀,國外已從直升機(jī)吊掛的基礎(chǔ)研究發(fā)展到對(duì)改善直升機(jī)吊掛飛行品質(zhì)的新方法和新型吊掛方式的研究。而國內(nèi)對(duì)直升機(jī)吊掛飛行的研究主要集中在理論探索方面,將直升機(jī)、載荷和吊索視為一個(gè)多體動(dòng)力學(xué)系統(tǒng),導(dǎo)致直升機(jī)的飛行動(dòng)力學(xué)建模要根據(jù)多體動(dòng)力學(xué)建模要求進(jìn)行簡化,以降低多體動(dòng)力學(xué)建模的復(fù)雜性。這些模型雖然適用于特定的分析工作,但較難根據(jù)不同的吊掛配置形式建立通用的系統(tǒng)動(dòng)力學(xué)模型。
隨著無人直升機(jī)的應(yīng)用越來越廣泛,大中型無人直升機(jī)的發(fā)展步伐正在不斷加快,無人直升機(jī)吊掛運(yùn)輸將得到越來越多的應(yīng)用。國外在這方面的研究較早,已經(jīng)實(shí)現(xiàn)無人直升機(jī)吊掛運(yùn)輸。2011年,美國K-MAX無人直升機(jī)在世界上首次完成了吊掛運(yùn)輸任務(wù)。國內(nèi)在這方面的研究剛剛起步,正在加大加快無人直升機(jī)吊掛運(yùn)輸技術(shù)的應(yīng)用研究。本文針對(duì)無人直升機(jī)吊掛運(yùn)輸飛行,采用自抗擾控制(ADRC)方法,設(shè)計(jì)了巡航狀態(tài)下吊掛飛行協(xié)調(diào)控制和目標(biāo)點(diǎn)附近吊掛消擺軌跡規(guī)劃控制策略,并進(jìn)行了仿真驗(yàn)證。
1 直升機(jī)吊掛系統(tǒng)耦合動(dòng)力學(xué)建模
首先建立無人直升機(jī)吊掛物的動(dòng)力學(xué)模型。如圖1所示,θ
、φ
分別表示吊掛物相對(duì)于機(jī)體的三維空間中的擺動(dòng)角度,l
為吊掛繩長。有效載荷動(dòng)力學(xué)的方程非常復(fù)雜,必須執(zhí)行許多數(shù)學(xué)計(jì)算。為了簡化計(jì)算,我們將其條件線性化,設(shè)所有耦合和高階項(xiàng)都為0。另外,可以假設(shè)以小角度狀態(tài)飛行,其中sinφ
=φ
,cosφ
=0,并且假設(shè)阻力為0。最終由拉格朗日法得到吊掛系統(tǒng)的線性化模型。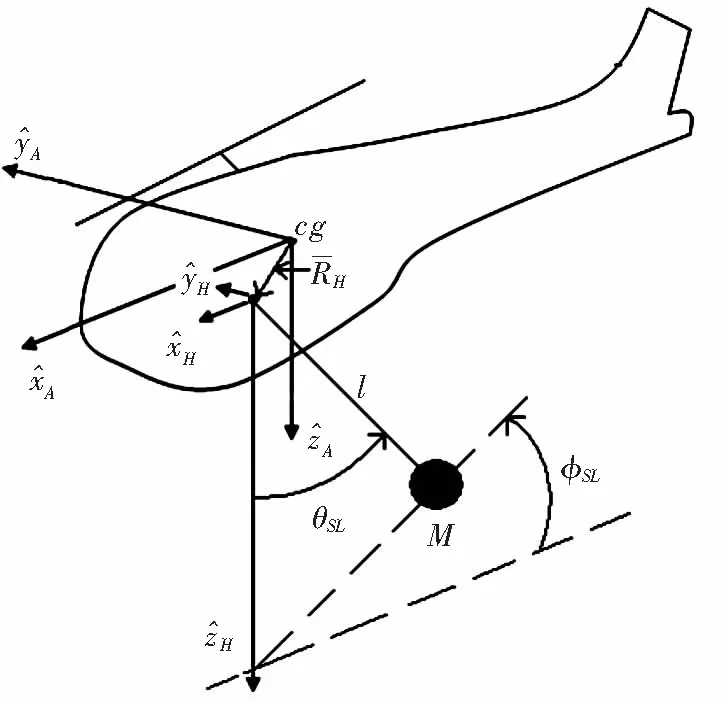
圖1 無人直升機(jī)吊掛模型
由拉格朗日方程得:
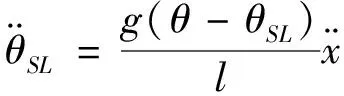
(1-1)
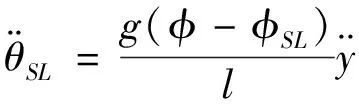
(1-2)
直升機(jī)吊掛耦合系統(tǒng)運(yùn)動(dòng)學(xué)可由如下方程表示:
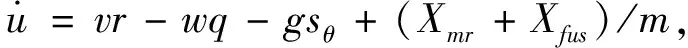
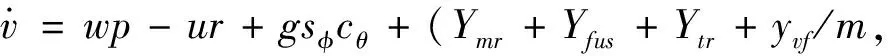
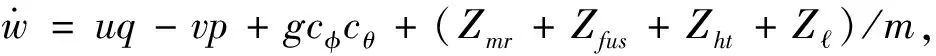
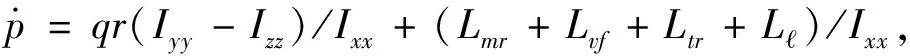
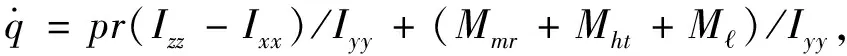
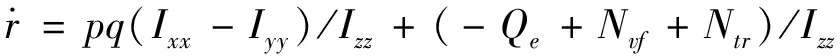
(1-3)
其中,Z
為吊掛系統(tǒng)在無人直升機(jī)Z
方向上的拉力,M
為吊掛系統(tǒng)施加給無人直升機(jī)的俯仰力矩,L
為吊掛系統(tǒng)施加給無人直升機(jī)的滾轉(zhuǎn)力矩。2 運(yùn)輸巡航狀態(tài)下吊掛飛行協(xié)調(diào)控制
運(yùn)輸巡航飛行狀態(tài)包括平飛、爬升、協(xié)調(diào)轉(zhuǎn)彎等多種飛行模態(tài)。如何確保無人直升機(jī)的吊掛飛行安全,是飛行控制系統(tǒng)必須要解決的問題。這對(duì)吊掛無人直升機(jī)的協(xié)調(diào)控制提出了更高的要求。在這種情況下,既要保證無人直升機(jī)的穩(wěn)定性,不能受吊掛物擾動(dòng)的影響太大,同時(shí)又要保持吊掛物與無人直升機(jī)相對(duì)穩(wěn)定,保證吊掛物不能超過最大擺動(dòng)幅度。
無人直升機(jī)本身的特性決定了其是一個(gè)不確定、強(qiáng)耦合和易受干擾的被控對(duì)象。實(shí)現(xiàn)良好的飛行特性,這對(duì)設(shè)計(jì)的飛行控制系統(tǒng)的性能提出了很高的要求,控制器控制能力直接決定了無人機(jī)的飛行品質(zhì)。傳統(tǒng)的PID 控制很難解決無人直升機(jī)這一類被控對(duì)象的控制問題;使用先進(jìn)控制方法如模糊控制、反步法控制、自適應(yīng)控制,雖然可以滿足直升機(jī)的飛行控制需求,但是上述方法設(shè)計(jì)困難,參數(shù)整定是個(gè)復(fù)雜的難題。ADRC 控制器對(duì)控制對(duì)象的數(shù)學(xué)模型要求卻不高,其包含的擴(kuò)張觀測器(ESO)設(shè)計(jì)思路是利用系統(tǒng)輸入和輸出重構(gòu)出系統(tǒng)狀態(tài),可以將內(nèi)部和外部干擾,甚至系統(tǒng)不確定的部分都當(dāng)作擾動(dòng),再去消除掉這個(gè)擾動(dòng)。
2.1 ADRC控制算法的原理及特點(diǎn)
自抗擾控制算法是在PID控制器的基礎(chǔ)上改良得到的一種全新控制算法。它既繼承了傳統(tǒng)PID控制的精髓(基于反饋控制,不需要被控對(duì)象的精確模型),又融合了眾多現(xiàn)代控制理論的思想,通過一種改進(jìn)的狀態(tài)觀測器來獲取被控對(duì)象的狀態(tài),觀測模型外擾動(dòng),達(dá)到更好的控制效果。ADRC控制器結(jié)構(gòu)示意見圖2。
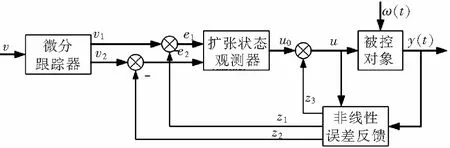
圖2 ADRC控制器結(jié)構(gòu)
圖2中,v
為指令輸入,v
為指令輸入過渡過程,v
為指令輸入過渡過程的微分,ω
(t
)為外界干擾,z
為實(shí)際輸入,z
為實(shí)際輸入的微分,z
為誤外界擾動(dòng)補(bǔ)償量,u
為實(shí)際控制量輸出。自抗擾控制器由跟蹤微分器、狀態(tài)擴(kuò)張器和非線性反饋控制律三個(gè)部分組成。它的核心部分是擴(kuò)張狀態(tài)觀測器。其中,跟蹤微分器的作用是安排過渡過程,擴(kuò)張狀態(tài)觀測器則用來估計(jì)系統(tǒng)狀態(tài)、模型和外擾。非線性反饋控制率是把未知外擾的非線性不確定對(duì)象用非線性狀態(tài)反饋化為“積分串聯(lián)型”,是一種對(duì)非線性不確定對(duì)象實(shí)現(xiàn)反饋線性化的結(jié)構(gòu),而且是一種動(dòng)態(tài)反饋線性化。
從ADRC的提出至今,許多實(shí)物試驗(yàn)和仿真試驗(yàn)都證明了ADRC能夠獲得良好的動(dòng)態(tài)性能且具有良好的性能魯棒性。自抗擾控制器的獨(dú)特思想和結(jié)構(gòu)決定了該方法具有如下優(yōu)點(diǎn):
一是結(jié)構(gòu)簡單。該方法具有與傳統(tǒng)PID非常相近的簡單結(jié)構(gòu),易于被工程人員掌握。例如線性形式的3階ADRC(指ADRC中的ESO階數(shù)為3),可以看成是一個(gè)比例微分(PD)控制器加上擴(kuò)張狀態(tài)(z
)的觀測和補(bǔ)償,當(dāng)信號(hào)z
被去掉時(shí)控制器則完全轉(zhuǎn)為PD控制器。二是反應(yīng)敏捷。傳統(tǒng)PID控制都要等到誤差發(fā)生后才能去補(bǔ)償控制;而ADRC則將觀察到的擾動(dòng)第一時(shí)間補(bǔ)償?shù)捷敵龆恕6遥琍ID中的微分項(xiàng)D,雖然說有預(yù)測功能,但它僅僅是將本次的誤差減去上一次的誤差,得到很粗劣的微分結(jié)果;而ADRC使用跟蹤微分器,準(zhǔn)確跟蹤目標(biāo)值的微分(圖中的跟蹤加速度),用擴(kuò)張狀態(tài)觀測器得出實(shí)際值的微分(圖中的觀測加速度),兩個(gè)相減即為準(zhǔn)確的誤差微分。
三是不依賴于對(duì)象模型,具有很強(qiáng)的適應(yīng)性。ADRC適用于從對(duì)對(duì)象模型一無所知到完全掌握對(duì)象模型的任何情況。當(dāng)然,如果能準(zhǔn)確捕捉到這個(gè)關(guān)系,ADRC工作強(qiáng)度將減輕,效果更佳。
四是很強(qiáng)的抗干擾能力。將系統(tǒng)的非線性、模型不確定性和外部擾動(dòng)等都視為系統(tǒng)的擴(kuò)張狀態(tài)加以觀測,然后利用控制率進(jìn)行補(bǔ)償。
五是解耦特性。對(duì)于MIMO系統(tǒng),自抗擾PID控制方法將系統(tǒng)變量間的各種耦合作用統(tǒng)一看成系統(tǒng)的擴(kuò)張狀態(tài)加以考慮,從而避免了需要單獨(dú)設(shè)計(jì)靜態(tài)或動(dòng)態(tài)解耦模塊后才能設(shè)計(jì)控制器的窘境,同時(shí)又不降低控制系統(tǒng)的性能。
六是易用性。ADRC在最初推出時(shí)雖然性能驚人,但是要調(diào)試的參數(shù)非常多,不容易使用。隨著Scaling and Bandwidth-Parameterization等理論的提出,ADRC參數(shù)調(diào)整變得簡單多了。
七是靈活性。ADRC是在PID的啟發(fā)下發(fā)展出來的,一般只要有PID的地方,都可以直接用ADRC替換。
2.2 控制器設(shè)計(jì)
飛行控制器采用雙閉環(huán)控制策略,內(nèi)環(huán)為姿態(tài)控制,外環(huán)為位置控制(見圖3)。位置ADRC輸入量為實(shí)際位置(x
,y
,z
)與期望位置(x
,y
,z
),輸出量是期望姿態(tài)角(φ
,θ
)和控制量U
。姿態(tài)ADRC根據(jù)期望姿態(tài)與實(shí)際姿態(tài)關(guān)系得到三個(gè)方向的控制量(U
,U
,U
)。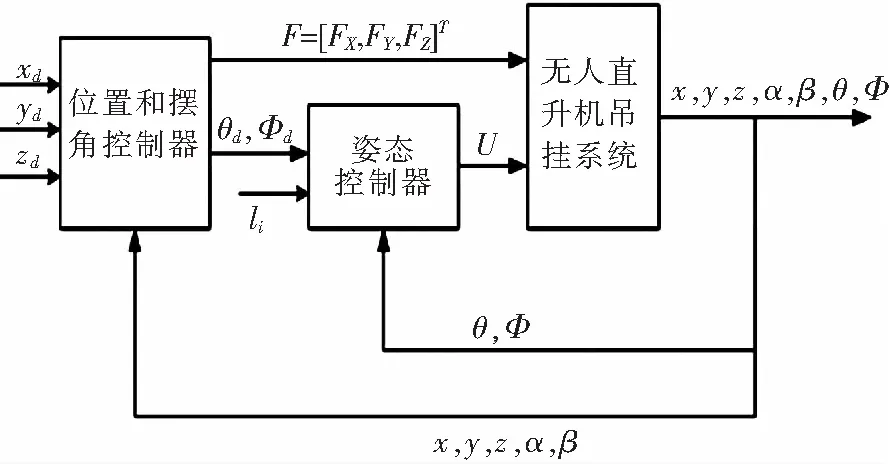
圖3 控制器整體結(jié)構(gòu)框圖
2.2.1 內(nèi)環(huán)ADRC控制器設(shè)計(jì)
對(duì)無人直升機(jī)內(nèi)環(huán)通道分別應(yīng)用ADRC控制策略(見圖4),控制器根據(jù)期望姿態(tài)與實(shí)際姿態(tài)關(guān)系得到三個(gè)方向的控制量(U
,U
,U
)。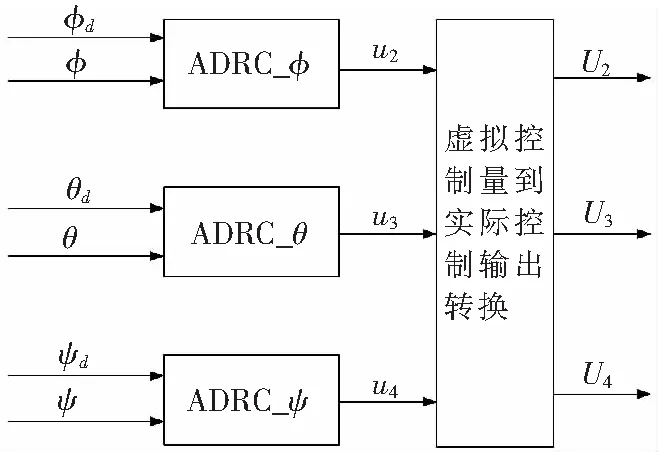
圖4 內(nèi)環(huán)ADRC控制器結(jié)構(gòu)框圖
以內(nèi)環(huán)滾轉(zhuǎn)角回路控制器為例,借助于ESO估計(jì)出的回路擾動(dòng)量,對(duì)系統(tǒng)進(jìn)行動(dòng)態(tài)補(bǔ)償,可以使得滾轉(zhuǎn)角回路近似為積分串聯(lián)型系統(tǒng)。滾轉(zhuǎn)角回路ADRC算法如下:
1)安排過渡過程
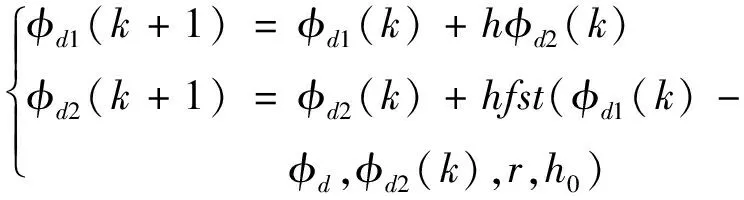
(2-1)
式中,r
為快速因子,h
為濾波因子。r
越大,跟蹤的速度越快,但噪聲放大也越大;h
越大,濾波效果越好,但跟蹤的效果變差。2)估計(jì)狀態(tài)和總擾動(dòng)(ESO方程)
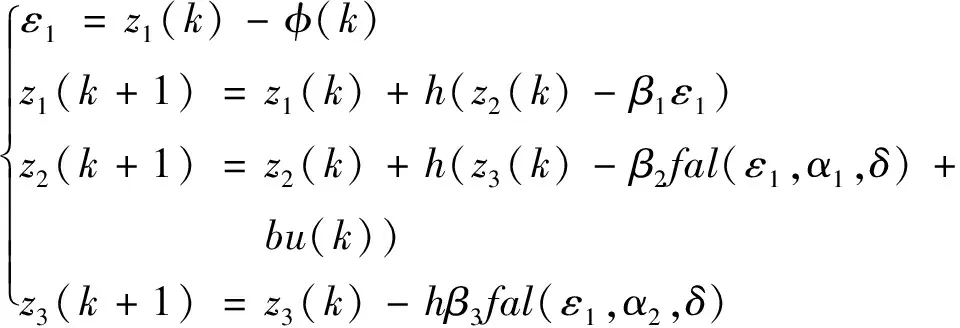
(2-2)
式中,β
、β
、β
為狀態(tài)誤差反饋的反饋增益,影響ESO的收斂速度;h
為控制周期,考慮到實(shí)際應(yīng)用,h
取為0.01;δ
為fal
函數(shù)的線性區(qū)間寬度,用來消除高頻脈動(dòng)的產(chǎn)生。3)控制量的形成
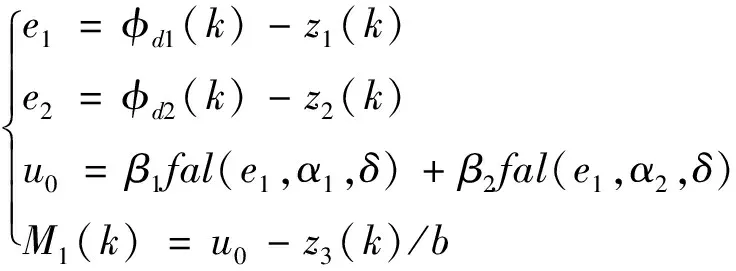
(2-3)
式中,M
為控制器計(jì)算輸出的滾轉(zhuǎn)力矩。2.2.2 位置環(huán)ADRC控制器設(shè)計(jì)
位置環(huán)ADRC控制器對(duì)直升機(jī)三個(gè)方向的位置分別進(jìn)行ADRC控制。位置ADRC輸入量為實(shí)際位置(x
,y
,z
)與期望位置(x
,y
,z
),得到三個(gè)方向的虛擬控制量。繼而通過虛擬控制量與實(shí)際控制輸出之間的轉(zhuǎn)換得到期望姿態(tài)角(φ
,θ
)和控制量U
。期望姿態(tài)角進(jìn)入姿態(tài)環(huán)進(jìn)行姿態(tài)環(huán)控制。位置環(huán)ADRC控制器結(jié)構(gòu)框圖見圖5。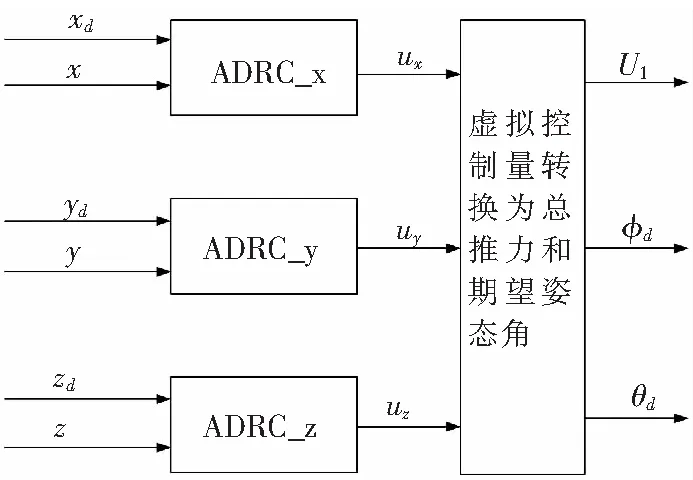
圖5 位置環(huán)ADRC控制器結(jié)構(gòu)框圖
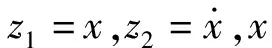
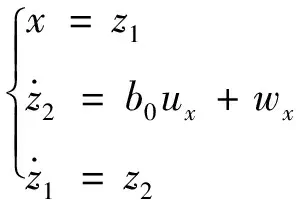
(2-4)
式中,w
為該通道總擾動(dòng),u
為虛擬控制量,b
為控制通道增益,此處為1。與姿態(tài)控制器類似,應(yīng)用TD安排過渡過程。TD 的輸入v
代表此處的x
,輸出(v
,v
)。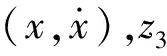
k
,k
)與PD控制器參數(shù)的意義相同。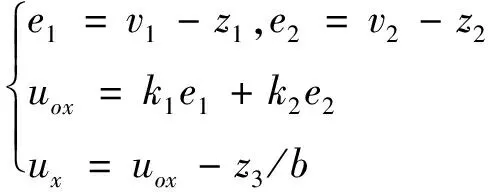
(2-5)
Y
方向與Z
方向的控制器設(shè)計(jì)與X
方向的方法一致。3 目標(biāo)點(diǎn)附近吊掛消擺軌跡規(guī)劃控制
無人直升機(jī)吊掛運(yùn)輸旨在將其吊掛的負(fù)載平穩(wěn)、安全、高效地運(yùn)送至指定位置。欠驅(qū)動(dòng)系統(tǒng)由于獨(dú)立控制量數(shù)目少于系統(tǒng)自由度,從而給其控制帶來了很大的困難。而無人直升機(jī)吊掛運(yùn)輸系統(tǒng)具有典型的欠驅(qū)動(dòng)特性,負(fù)載不能直接通過驅(qū)動(dòng)器控制,而只能通過對(duì)無人直升機(jī)的運(yùn)動(dòng)進(jìn)行設(shè)計(jì)來間接控制負(fù)載的運(yùn)動(dòng)。我們需要無人直升機(jī)在通過航跡規(guī)劃到達(dá)目標(biāo)點(diǎn)時(shí)進(jìn)行卸載、著陸作業(yè),但此時(shí)吊掛物很可能在不斷地?cái)[動(dòng),這會(huì)影響無人直升機(jī)的穩(wěn)定性,出現(xiàn)危險(xiǎn)。為了防止此類現(xiàn)象出現(xiàn),確保作業(yè)安全性,希望無人直升機(jī)在到達(dá)目的地后,吊掛負(fù)載無殘余擺動(dòng)。充分考慮無人直升機(jī)吊掛運(yùn)輸?shù)乃俣取⒓铀俣鹊任锢砑s束,以及無人直升機(jī)與吊掛物之間的非線性耦合關(guān)系,采用S曲線生成法進(jìn)行動(dòng)態(tài)規(guī)劃控制,消除吊掛物的殘余擺動(dòng)。
3.1 S曲線算法原理
典型S型曲線的速度、加速度以及加加速度隨時(shí)間變化曲線如圖6所示。其中,v
為系統(tǒng)最大速度,a
為系統(tǒng)最大加速度,j
為系統(tǒng)加加速度,t
為加加速時(shí)間,t
為加速時(shí)間,t
為總運(yùn)動(dòng)時(shí)間。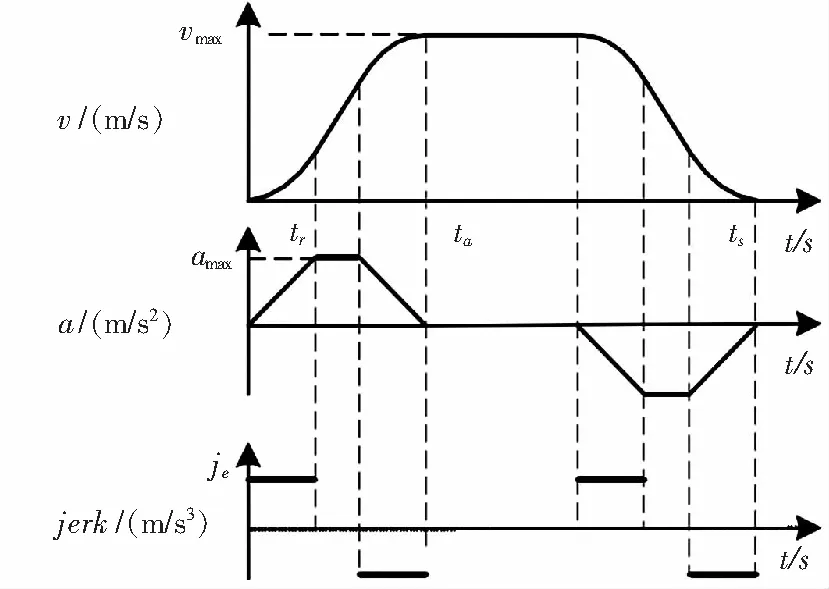
圖6 典型S曲線圖
對(duì)任意時(shí)刻,S型曲線的位移、速度、加速度可表示為:
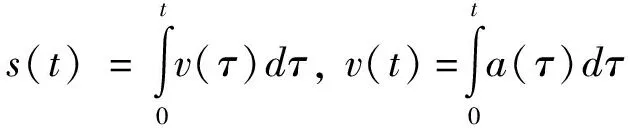
(3-1)
a
(t
)=
(3-2)
3.2 軌跡策略生成
該軌跡如圖7所示。其中參數(shù)分別表示加速區(qū)間,勻速區(qū)間,減速區(qū)間以及最高速度。
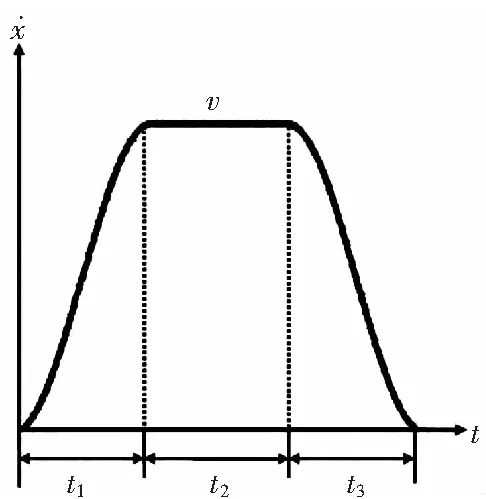
圖7 S型曲線速度軌跡
S型曲線速度軌道為:
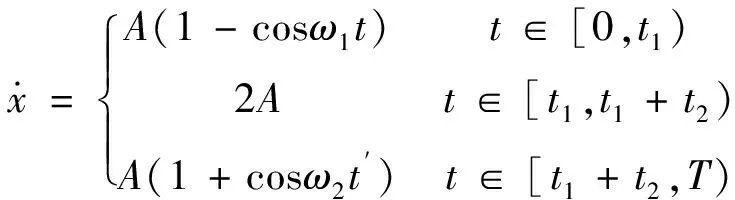
(3-3)
式中,A
=v/
2,ω
=π/t
,ω
=π/t
,t
=t
-t
-t
,T
=t
+t
。取式(3-3)的時(shí)間導(dǎo)數(shù),得到其加速度軌跡:
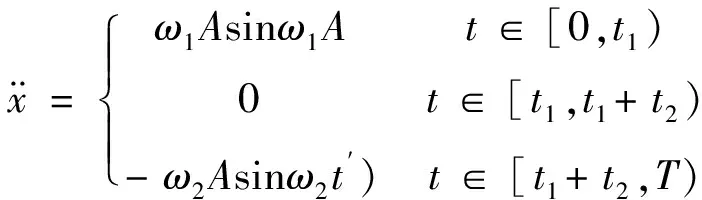
(3-4)
為了驗(yàn)證算法,出于可靠性,我們只考慮二維平面擺動(dòng)情況,即只對(duì)θ
進(jìn)行消擺處理。
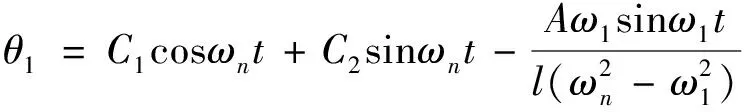
(3-5)
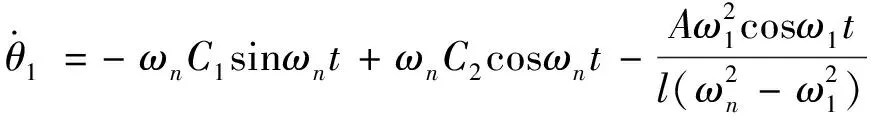
(3-6)
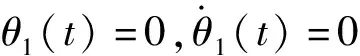
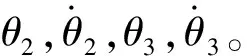
θ
(T
)=0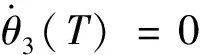
(3-7)
4 仿真驗(yàn)證
4.1 運(yùn)輸巡航狀態(tài)下吊掛飛行協(xié)調(diào)控制仿真
在Matlab仿真環(huán)境下,對(duì)運(yùn)輸巡航狀態(tài)下吊掛飛行協(xié)調(diào)控制算法進(jìn)行仿真驗(yàn)證,結(jié)果如圖8、圖9。

圖8 運(yùn)動(dòng)狀態(tài)下的橫向跟蹤情況

圖9 運(yùn)動(dòng)狀態(tài)下的縱向跟蹤情況
圖8中綠線表示動(dòng)態(tài)時(shí)使用ADRC的橫滾角速率設(shè)定值,黑線表示動(dòng)態(tài)時(shí)使用ADRC的橫滾角速率測量值。
圖9中綠線表示動(dòng)態(tài)時(shí)使用ADRC的俯仰角速率設(shè)定值,黑線表示動(dòng)態(tài)時(shí)使用ADRC的俯仰角速率測量值。
仿真結(jié)果表明,動(dòng)態(tài)響應(yīng)的響應(yīng)時(shí)間基本都在60~80ms之間,超調(diào)量很小。在恢復(fù)到穩(wěn)態(tài)時(shí),ADRC控制的無人直升機(jī)飛行平穩(wěn),跟蹤性能良好,靜態(tài)誤差很小。
4.2 目標(biāo)點(diǎn)附近吊掛消擺軌跡規(guī)劃控制仿真
在Matlab仿真環(huán)境下,對(duì)目標(biāo)點(diǎn)附近吊掛消擺軌跡規(guī)劃控制算法進(jìn)行仿真驗(yàn)證,結(jié)果如圖10-圖12。
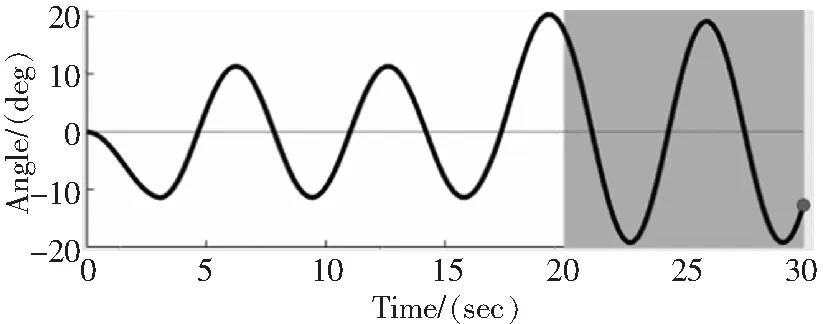
圖10 吊掛負(fù)載擺動(dòng)角度

圖11 無人機(jī)平移規(guī)劃運(yùn)動(dòng)軌跡
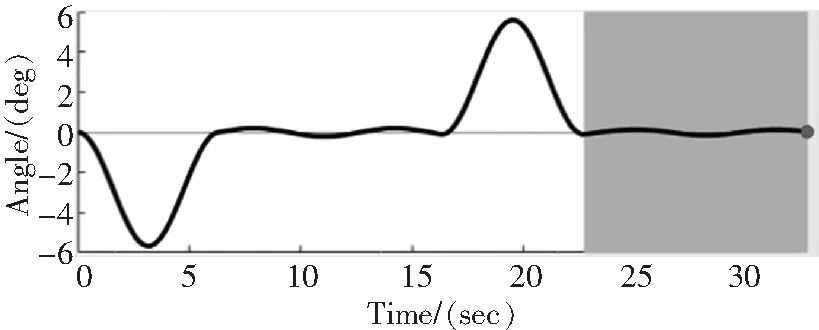
圖12 吊掛負(fù)載擺動(dòng)角度
1)無軌跡規(guī)劃下的吊掛物擺動(dòng)情況
仿真結(jié)果表明,在沒有軌跡規(guī)劃的情況,在20s時(shí),當(dāng)無人直升機(jī)達(dá)到預(yù)設(shè)位置停止后,吊掛負(fù)載持續(xù)擺動(dòng)。
2)S曲線軌跡規(guī)劃下的吊掛物擺動(dòng)情況
仿真結(jié)果表明,在進(jìn)行S曲線軌跡規(guī)劃下,在20s時(shí),當(dāng)無人直升機(jī)達(dá)到預(yù)設(shè)位置停止后,吊掛負(fù)載停止擺動(dòng),且擺角基本保持在0°,消擺效果明顯。
5 結(jié)論
本文采用自抗擾控制技術(shù),引入虛擬控制量對(duì)位置和姿態(tài)進(jìn)行控制解耦,應(yīng)用擴(kuò)張狀態(tài)觀測器進(jìn)行狀態(tài)解耦和擾動(dòng)估計(jì),較好地實(shí)現(xiàn)了無人直升機(jī)吊掛耦合系統(tǒng)的解耦,能夠較好地解決狀態(tài)耦合、外部擾動(dòng)和被控對(duì)象參數(shù)攝動(dòng)等問題。仿真驗(yàn)證說明,無論是在動(dòng)態(tài)特性還是穩(wěn)態(tài)特性上,自抗擾控制都具有較好的抗干擾能力與穩(wěn)定性。因此,自抗擾控制器應(yīng)用于無人直升機(jī)吊掛運(yùn)輸飛行協(xié)調(diào)控制是可行的,對(duì)于擾動(dòng)的控制也是有效的。

