基于LS-SVM的煤炭建設項目投資估算模型研究

寧 暉

(中煤能源研究院有限責任公司，陜西 西安 710054)

投資估算是在項目決策階段，以方案設計為依據，按照規定的程序和方法，對擬建項目所需總投資及其構成進行的預測和估計。估算投資作為論證擬建項目的重要經濟指標，既是建設項目技術經濟評價的基礎，又是該項目在實施階段投資控制的目標值[1-2]。因此，全面準確快速地對建設項目投資進行估算，是科學、客觀、有效地進行項目決策的關鍵。投資估算方法較多，各有其適用的條件和范圍，一般可采用的估算方法有簡單匡算法和分類詳細估算法[1-2]。簡單匡算法計算簡單、速度快，但估算誤差往往較大；分類詳細估算需要以詳細的工程資料為基礎，估算精度高，但涉及專業多，工作量大，耗費時間較多。在項目前期決策階段，尤其是投資機會研究和初步可行性研究階段，往往獲取的項目信息較少、設計深度不足、工程資料欠缺、時間要求緊迫，無法直接采用詳細指標法進行分類估算，但這一階段的投資估算對企業決策影響較大。為了在項目前期工作中，能夠快速、準確估算項目的建設投資，在收集大量投資數據的基礎上，本文提出了采用數據挖掘的方法和技術，建立起基于最小二乘支持向量機的投資估算模型。

1 基于最小二乘支持向量機的投資估算模型構建

支持向量機(support vector machine，SVM)是建立在統計學習理論基礎之上的新型機器學習方法，專門針對小樣本學習問題，以結構風險最小化為原則，在很大程度上克服了傳統機器學習方法中的過學習、 非線性、 維數災難以及局部極小值等問題， 有很強的非線性處理能力和良好的泛化性能，在社會經濟的多個領域都獲得越來越廣泛的研究和應用[3-5]。

1.1 最小二乘支持向量機基本原理

最小二乘支持向量機(least squares support vector machine，LS-SVM)作為SVM的改進和推廣，采用誤差項的平方，將不等式約束改成等式約束，最終求解線性方程組即可，避免了求解二次規劃問題，提高了求解問題的速度和收斂精度[5]。

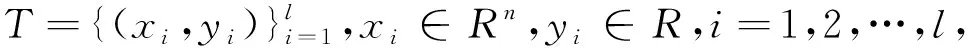
最小二乘支持向量回歸機可表述為式(1)和式(2)優化問題。

(1)

s.t.yi=(w×φ(xi))+b+ξi,i=1,…,l

(2)

式中：w為權向量；b為偏置；ξi為誤差項；C>0為正則化參數。為求解上述優化問題，引入Lagrange函數，見式(3)。

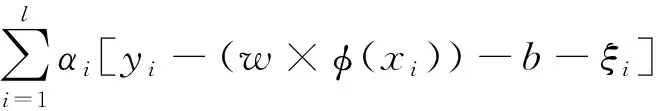
(3)

式中，α=(α1,α2,…,αl)T為拉格朗日乘子向量。

根據KKT條件，有式(4)～式(7)。

(4)

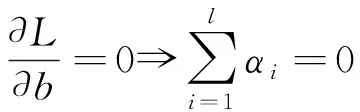
(5)

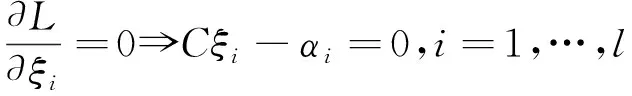
(6)

(7)

消去變量w和ξi,可得線性方程組，見式(8)。

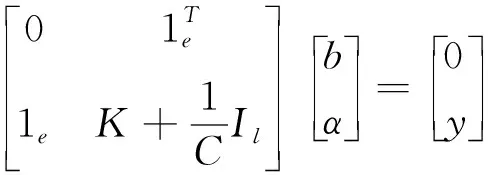
(8)

式中：1e=[1,1,…,1]T，y=(y1,y2,…yl)T；Il為l×l單位矩陣；K為核矩陣，見式(9)。

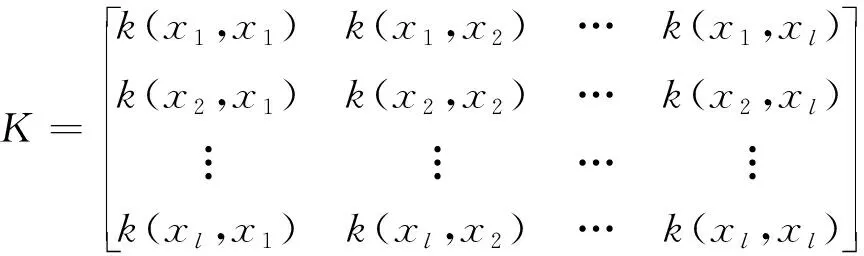
(9)

式中：k(xi,xj)=(φ(xi)×φ(xj))；i,j=1,2,…,l。

通過求解方程組，得到最優解α*和b*，進而可以得到最小二乘支持向量機的回歸函數，見式(10)。

(10)

在支持向量機算法中，選擇合適的核函數是關鍵的一步，核函數的種類較多，常用的有以下幾種。

線性核函數，見式(11)。

k(x,x′)=(x,x′)

(11)

多項式核函數，見式(12)。

k(x,x′)=((x,x′)+1)d

(12)

徑向基核函數(radial basis function，RBF)，見式(13)。

k(x,x′)=exp(-σ‖x-x′‖2)

(13)

1.2 算法流程設計

基于回歸預測的基本思想，應用最小二乘支持向量機進行項目投資估算的算法包括數據預處理、選擇最優參數、訓練模型及擬合預測四個步驟，流程如圖1所示。

圖1 基于LS-SVM的投資估算流程圖Fig.1 Flowchart of investment estimationbased on LS-SVM

基于LS-SVM的投資估算算法詳細描述如下所述。

第一步：數據預處理。對輸入樣本集W={(X1,Y1),(X2,Y2),…,(Xm,Ym)}進行數據清洗、數據規約等，消除噪聲數據如離群值或重復值等異常點、刪除不相關及冗余變量，并對數據進行[0,1]區間歸一化，得到數據集D={(x1,y1),(x2,y2),…,(xn,yn)}。

第二步：交叉驗證選擇參數。將數據集D隨機地分成包含l個樣本點的訓練集Train和包含k個樣本點的測試集Test,且l+k=n。

選取線性核或徑向基(RBF)核，學習最優的懲罰參數C與RBF核參數σ。

1) forC=2-10,2-9.5,2-9,…,29.5,210；

2) forσ=2-10,2-9.5,2-9,…,29.5,210(注：線性核無此參數循環)；

3) fori=1,…,10；

4) 將訓練集Train隨機分成10份，以其中9份合在一起建立模型，用剩余一份作為測試，計算出均方根誤差等評價指標；

5) End；

6) 計算10組實驗均方根誤差的平均值；

7) End；

8) End。

比較C和σ所有組賦值下的均方根誤差，選擇最小值對應的C和σ為最優參數。

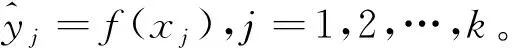
為了衡量算法的學習性能，常見的評價回歸算法性能的指標有均方根誤差(root mean squared error，RMSE)和決定性系數(R2)。 定義見式(14)和式(15)。

(14)

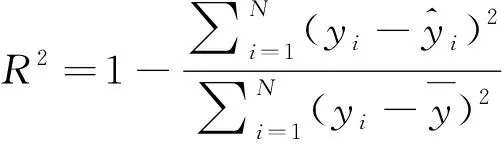
(15)

2 項目樣本特征選取

煤炭建設項目的投資受礦山地質條件(資源賦存深度、煤層結構及厚度、頂底板巖性等)、礦井技術條件(采煤方法、開拓方式、采掘工作機械化程度等)、項目廠址條件(交通、供水、供電、原材料供應等)、政策環境條件及價格市場條件等因素的影響[6-7]。不同條件下，投資水平的差異較大。以井工礦為主要研究對象，本文設置的主要特征包括項目地點、項目設計時間、設計生產能力、建設工期、設計階段、開拓方式、井筒施工方法、采煤方法(工藝)、采煤工作面、瓦斯等級、水文地質類型、煤層埋深、煤層傾角、是否為軟巖等主要信息。詳細見表1。本文提取特征主要從地質賦存和工藝設計等方面考慮了與投資關聯度較高的條件及因素，并且全部信息可以從項目設計文件中提取。在實際預測中，需要做進一步的數值分析，去除無關及冗余特征。

表1 井工礦主要特征表Table 1 Main features of coal mine

續表1

3 數據實驗

本文研究的建設投資中剔除了礦權價款、預備費及某些項目特有的費用等，并且礦井配套的鐵路專用線、礦井水深度處理或其他特殊工程的投資等均不包含在本次分析范圍之內。本文數據實驗所有程序在Matlab中編碼實現。

3.1 樣本收集

本次建模使用的礦井樣本數據主要來源于設計文件，包括可行性研究報告及初步設計等，共計45個，其中可研數據31個，初設數據14個。項目所在地區涵蓋了陜西省(榆林市、府谷縣、咸陽市)、山西省(晉中市、晉城市、太原市)、內蒙古自治區(鄂爾多斯市)、新疆維吾爾自治區(哈密市、塔城市、伊犁哈薩克自治州)、甘肅省、貴州省、云南省、青海省等主要產煤地區；項目設計生產規模主要集中在1.2～15.0 Mt/a范圍內；開拓方式以立井和斜井開拓為主。樣本具有較強的代表性和較好的學習價值。

3.2 數據預處理

首先，在對所有字符性變量進行數值化處理的基礎上，分別繪制了設計生產能力、開拓方式、設計時間和項目地點四個變量與噸煤投資的關系箱體圖[8]，如圖2所示。由圖2可知，不同維度下的投資分布特征，通過觀察和對比，初步判斷第35個樣本點為異常點。其次，對所有變量進行了關聯分析，計算了兩兩變量間的Pearson相關系數[8]，見表2。由表2可知，設計生產能力與噸煤投資關聯度最大，為負相關關系；而設計階段、水文地質類型與建設投資的相關系數均小于0.3，表示關系極弱，認為不相關。最后，對數據進行[0,1]區間歸一化，轉換函數，見式(16)[9]。

表2 變量相關系數表Table 2 Variable correlation coefficient

圖2 主要變量與噸煤投資的關系箱體圖Fig.2 Box diagram of the relationship between main variables and tons of coal investment

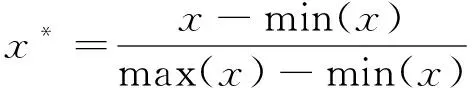
(16)

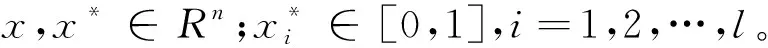
3.3 模型建立與預測結果

按照交互驗證的方法選擇最優參數，將訓練樣本集合隨機分成10份，其中9份合在一起建立模型，用剩余1份作為測試。這樣，最小二乘支持向量機在10組不同的訓練集和測試集上進行實驗，取10次實驗的平均結果作為預測結果。

由表3可知，采用線性核函數和RBF核函數的最小二乘支持向量回歸機所得的確定性系數R2都超過了0.9，MSE值分別為0.005 0和0.003 3，預測結果良好。但相比較，采用RBF核函數的最小二乘支持向量回歸機在井工礦噸煤投資估算上獲得了更優的預測精度。

表3 模型最優參數與評價指標結果表Table 3 Model optimal parameters and evaluationindex results

最優參數選定后，利用兩種核函數在35個訓練樣本集上分別進行模型訓練，得到各自的最優決策函數，再通過最優決策函數分別對8個測試樣本點進行預測，預測結果見表4、圖3和圖4。

表4 井工礦噸煤投資預測結果Table 4 Forecast results of coal mine investment 單位：元/t

由表4可知，使用RBF核函數的最小二乘支持向量回歸機在測試集上預測的最大相對誤差為24.43%，不超過投資機會研究階段投資估算的允許誤差率30%[7]；預測相對誤差介于10%～20%之間的有兩個樣本點，分別為17.79%和19.98%，低于初步可行性研究(項目建議書)階段投資估算的允許誤差率20%[7]；其余5個測試樣本點的預測相對誤差全部小于可行性研究階段投資估算的允許誤差率10%[7]，最小相對誤差為1.83%；預測的相對誤差平均值為10.95%。

由圖3和圖4也可以看出，該模型具有較高的預測精度和較強的泛化性能。但相比較，采用RBF核函數的最小二乘支持向量回歸機的預測值和真實值具有更好的吻合效果。

圖3 線性核函數預測結果Fig.3 Prediction results using linear kernel function

圖4 RBF核函數預測結果Fig.4 Prediction results using RBF kernel function

4 實例分析

除了隨機數據實驗，本文選取了山西省某礦井(2011年9月可研，斜井)、陜西省某礦井(2017年12月可研，斜井)、內蒙古自治區某一礦井(2018年3月初設，立井)、云南省某礦井(2015年9月初設，立井)、內蒙古自治區某二礦井(2012年3月初設，立井)等項目作為擬建項目，假設投資未知，分別用兩種核函數的最小二乘支持向量機算法和簡單匡算法中的生成能力指數法進行投資預測，結果見表5和圖5。

圖5 實際項目投資預測對比圖Fig.5 Comparison chart of actual project investment forecast

由表5可知，生產能力指數法預測誤差較大，對所有項目的投資預測精度均低于最小二乘支持向量回歸機算法。 而最小二乘支持向量回歸機算法除了對陜西某礦井的投資預測相對誤差高于10%以外，對其他項目采用兩種核函數預測的相對誤差全部小于10%，其中RBF核函數的整體性能優于線性核函數。

表5 實際項目投資預測結果對比表Table 5 Prediction results of actual project investment 單位：元/t

造成以上結果差異的主要原因在于兩種方法的預測原理存在本質區別：生產能力指數法預測項目投資時，只與搜尋到的目標項目有關，合適的目標項目是否存在以及其投資是否合理直接影響預測結果的準確性，另外，計算公式中的指數和綜合系數的確定受主觀經驗影響較大；支持向量機算法在去除數據集中異常數據點后，每次預測都會學習數據集中所有樣本的特征和投資之間的隱含關系，綜合了全部樣本信息，另外，模型中的參數以網格搜索的方式尋找最優，強調的是模型的泛化性能。

5 結 論

1) 本文模型技術特征提取簡單方便、迅速快捷，避免了分類指標估算時，技術人員詳細設計各單體工程技術參數與具體工程量的過程，節省了估算時間，提高了工作效率。

2) 本文模型訓練過程科學合理、準確高效，綜合了數據集中所有樣本數據(去除異常點)的全部信息，避免了依據類似項目進行投資估算時的主觀性和偏差性，降低了估算誤差。

3) 本文模型具有動態學習的優勢，隨著新的樣本數據不斷加入，可以不斷優化模型、更新估算投資，進一步提高預測精度。