非均質巖石單軸壓縮細觀模擬及破裂特征描述

馬萬里，陳世江

(內蒙古科技大學礦業研究院，內蒙古 包頭 014010)

巖石的非均質性向來都是國內外學者研究的重點，不同學者采用不同數值計算軟件對非均質巖石的破裂特征進行研究[1-2]。巖石的破裂特征對沖擊地壓、頂板冒落、巷道支護具有重要意義。

為了描述巖石的非均質性，不同學者采用不同的方式進行刻畫，唐春安等[3]通過假設巖石參數服從Weibul方式對巖石彈性模量、抗壓抗拉強度進行賦值；田志等[4]通過數字巖石物理的形式對地層沉積過程中的非均質性進行表征；羅榮等[5]通過蒙特卡洛法對巖石非均質性進行描述；陳沙等[6]以圖像處理為媒介，利用Matlab灰度識別獲取巖石的截面特征，實現了巖石的非均質表征。隨著計算機分析手段的進化，CT掃描三維重構技術得到了極大的發展，不同研究方向學者以CT掃描技術為基礎，研究了巖石的細觀破壞、滲流、結構變化等，獲得了較多有益成果，極大發展了巖石力學[7-9]。巖石破裂方面：謝和平等[10]以能量耗散角度對巖石破裂過程不同階段進行了精細刻畫；程昊等[11]采用C++對FLAC進行二次開發，實現了巖石破裂過程中聲發射參量導出；朱澤奇等[12]分析了花崗巖破裂及聲發射特性，明確了非均質對巖石局部應變產生重要影響；霍丙杰等[13]以FLAC數值計算軟件分析了房式采空區煤柱塑性區分布規律，明確了煤柱拉剪復合破壞機制。為了更好地描述巖石每個單元的破碎程度，基于單元損傷、單元安全度、破壞接近度等描述巖石應力狀態及三維重構裂隙越來越來受到人們的重視[14-15]，朱萬成等[16]以彈性損傷建立了非均質巖石應力-損傷本構模型；王峰[17]以MC準則為基礎，定義了以單元應力狀態點距包絡線距離為基礎的破壞接近度概念。

以上研究豐富和發展了巖石非均性表征方法和巖石破裂過程中裂隙演化、能量釋放特征，巖石的非均質性同樣對水力壓裂、爆破等有著重大影響，建立了基于MC準則的應變軟化本構模型，通過FLAC內嵌的FISH語言及Matlab編程，實現了巖石的非均質賦參及彈性模量、內聚力、內摩擦角隨塑性應變弱化，探討了不同均質度巖石破裂過程及不同裂隙處理方式的優缺點，為今后非均質爆破試驗及數值計算提供基礎性工作。

1 非均質巖石應變軟化本構模型建立及驗證

1.1 巖石非均質性的描述

煤巖體物理力學性質和顆粒分布、缺陷、節理等分布表現出較強的差異性，局部應力、應變導致不同位置應力分布不同，假設其彈性模量、內聚力、內摩擦角、抗拉強度等參數服從weibul分布，且無相關性，可表示為式(1)[18]。

(1)

式中：ε*為微元強度；m為均質度系數，表征巖石的非均質程度，其值越大，表明巖石均質性較高；M為某一力學參數的均值，表征了巖石某一力學性能強度。

1.2 基于MC準則的應變軟化本構模型

FLAC3D內置MC本構模型為理想彈塑性模型，即進入塑性階段后應力隨著應變的增加保持不變，很難描述巖石的應變軟化過程。其內置的應變軟化模型是基于單元的塑性剪切應變對單元的內聚力、內摩擦角、膨脹角的參數進行弱化，對拉破壞單元的適用性較弱，因此，本文在FLAC內置應變軟化模型基礎上進行修正，建立以塑性應變為參數弱化依據參量，則其內聚力、內摩擦角、彈性模量與塑性應變關系可表示為式(2)。

(2)

式中：c0、φ0、E0和cr、φr、Er分別為初始和殘余內聚力、內摩擦角、彈性模量；εp*為初始和殘余彈性模量數值之和一半對應的塑性應變。

因此，修正后的MC準則為式(3)[19]。

(3)

式中：Nφ=(1+sinφ)/(1-sinφ)；φ為摩擦角；c為內聚力；σt為抗拉強度；c(εp)為隨塑性應變變化的內聚力，εp為0時表示巖石材料處于彈性階段，εp大于0時表示巖石進入塑性階段，此時其內聚力、內摩擦角、彈性模量等參數將發生弱化。

若以內聚力的弱化程度對損傷變量進行描述，損傷變量定義為式(4)。

(4)

根據連續介質損傷力學理論，其本構關系可以表示為式(5)[20]。

σ=Eε(1-D)

(5)

結合式(1)～式(5)得到基于MC準則的非均質巖石應變軟化(應力-損傷)本構模型。

1.3 模型驗證

本文建立的應變軟化(應力-損傷)模型為多參數弱化本構模型，和FLAC內置應變軟化模型具有一定的相似性，為了驗證模型的合理性及正確性，通常需要實驗室試驗反演獲取模型各參數數值，然后將實驗室和FLAC數值計算結果進行對比。由于未進行實驗室試驗，為了驗證模型的可行性，本文以單參量軸向應變(F)作為微元強度值衡量巖石損傷程度，并和楊圣奇等[21]試驗數據進行對比，對比結果及參數取值見圖1。由圖1可知，理論模型無法體現巖石壓縮過程中的初始壓密階段，彈性階段匹配性較高，同時屈服破壞階段應力跌落貼合度較高。巖石單軸壓縮表現出較強的彈脆性，均值度m取值較大，為了理論曲線和實驗室曲線較為接近，同樣可能導致模型參數的失真，但總體上驗證了模型的可行性和正確性，表明本文建立模型具有較強的適用性，可以反映巖石全應力-應變整個過程。

圖1 實測曲線-理論曲線對比Fig.1 Comparison of measured curve and theoretical curve

2 非均質巖石破裂特征數值計算

2.1 數值計算模型建立及邊界條件

為了驗證將上文建立的非均質巖石應變軟化本構模型引入FLAC，分析巖石非均質性對巖石破裂特征影響及破裂特征描述，本小節建立數值計算模型尺寸為100 mm×50 mm×50 mm立方體模型(圖2)，模型一共25 000個網格，上下表明施加位移速度邊界5e-7m/step。初始參數見表1，同時計算過程中對彈性單元數量、能量進行監測。

圖2 數值計算模型Fig.2 Numerical calculation model

表1 單軸抗壓有限差分法模擬數據Table 1 Simulation data of uniaxial compressionfinite difference method

2.2 非均質性及應變軟化求解過程

為了表征巖石的非均質性，本文通過Matlab編程生成weibul函數txt文件，數據點和單元網格數量保持一致，通過FLAC讀取文件的形式實現對不同參數的對應賦參，同時由于本文不考慮數據點之間的關聯性，因此采用多個weibul數據文檔進行賦值。具體FISH編程思路為：將模型每個單元力學參數值和weibul函數txt文件數值進行一一對應，同時利用parse功能實現數據的分隔，并采用額外變量顯示，均質度為7的內聚力和內摩擦角分布特征見圖3。

圖3 巖石材料非均質描述Fig.3 Description of heterogeneity of rock material

建立FISH函數對單軸壓縮過程中單元內聚力、內摩擦角、彈性模量等參數與塑性應變關系進行描述，計算一步求解每個單元的塑性應變，并根據式(2)對模型各參數進行修改，并監測單元的彈塑性狀態、數量及彈性能，再計算一步并不斷循環，最終實現非均質巖石單軸壓縮破裂全過程數值計算，具體求解過程見圖4。

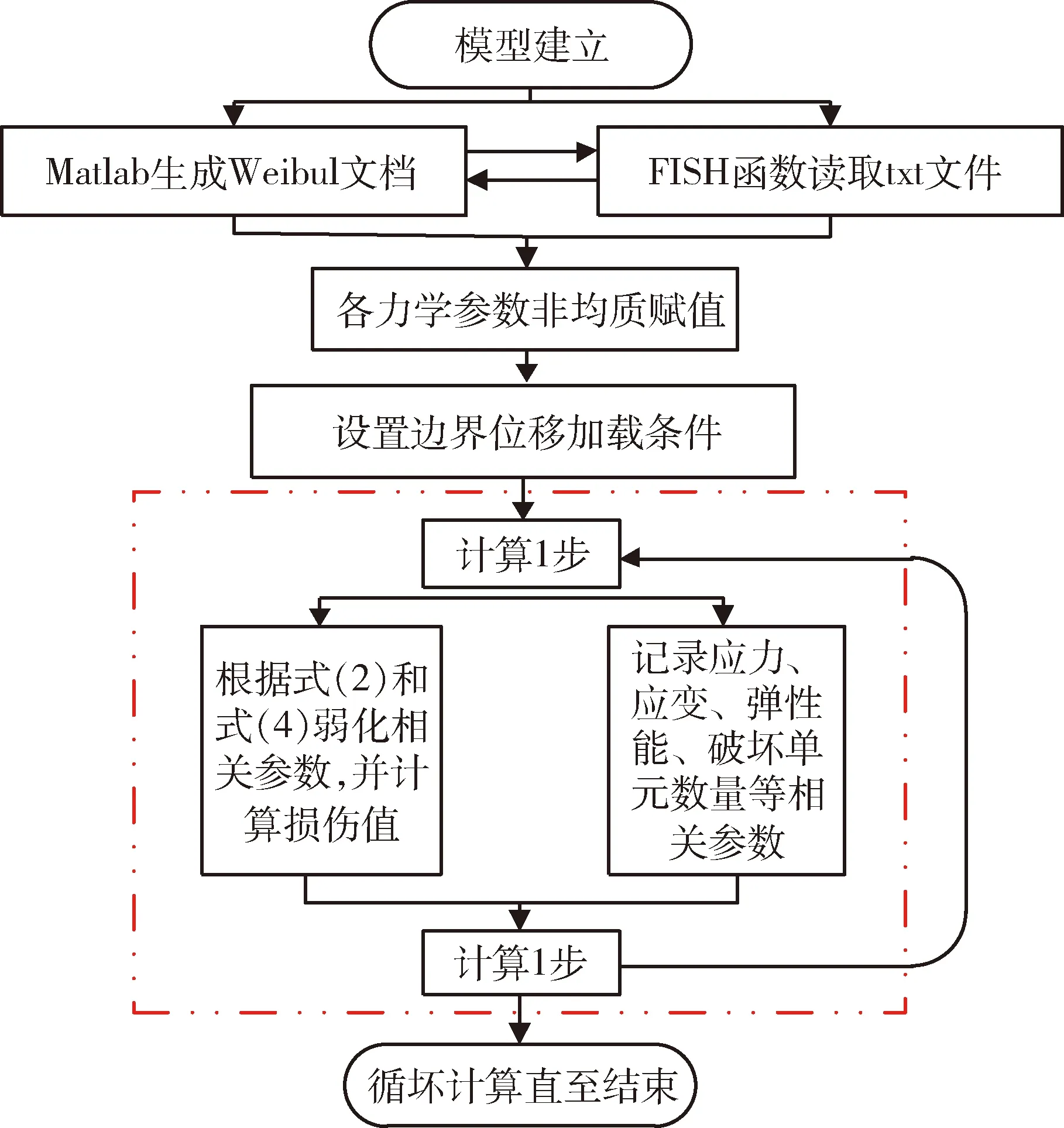
圖4 數值計算求解流程Fig.4 Numerical calculation flow

2.3 單軸壓縮全應力-應變各階段

以均質度m=7為例分析單軸壓縮過程中能量及裂隙演化全過程(圖5)，單軸壓縮初期，巖石內部缺陷較大的點即力學參數較弱的點發生破裂，但整體數量較小，呈隨機分布，隨著加載步數增大，破裂點數量不斷增大，巖石仍處于彈性階段，此時，破裂點開始出現匯集、融合等現象，這些為宏觀裂隙的出現提供了必要條件。巖石進入屈服階段后，開始出現大量拉伸破裂點，一旦進入破壞階段，大量單元狀態由正在剪切破壞狀態向過去剪切狀態轉變，破裂點從隨機分布的無序狀態向局部剪切帶形成的有序狀態演變，這和混沌理論較為一致，最終形成“X”型剪切帶。巖石彈性能演化和整個應力應變過程貼合度較高(圖6)，且在應力峰值時到達最大值，能量演化曲線呈現凹型演化和實驗室應力應變曲線較為類似。若以巖石破裂點作為聲發射參量，可以看出隨著加載步數的增加巖石的總破裂點基本恒定，且聲發射參量在巖石峰值時稍靠右側達到最大值，之后由于巖石大面積卸載，導致聲發射參量不斷減小，這個過程為巖石內部顆粒重新裝配過程，本文稱之為平靜期(圖7)。

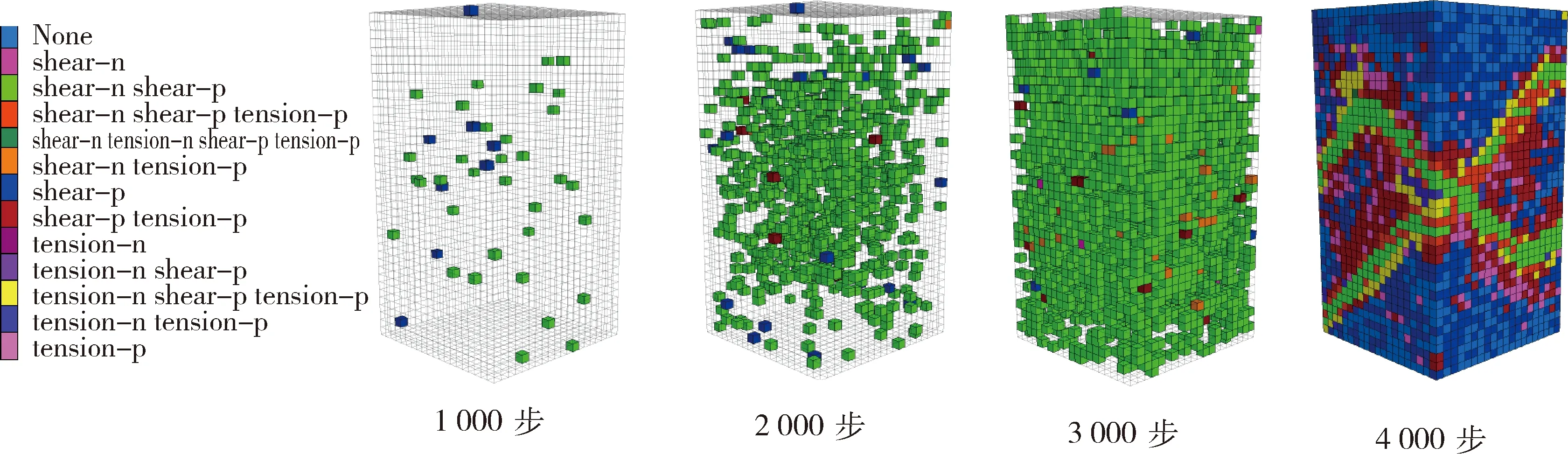
圖5 巖石破裂過程破裂點分布Fig.5 Distribution of fracture points in the process of rock fracture

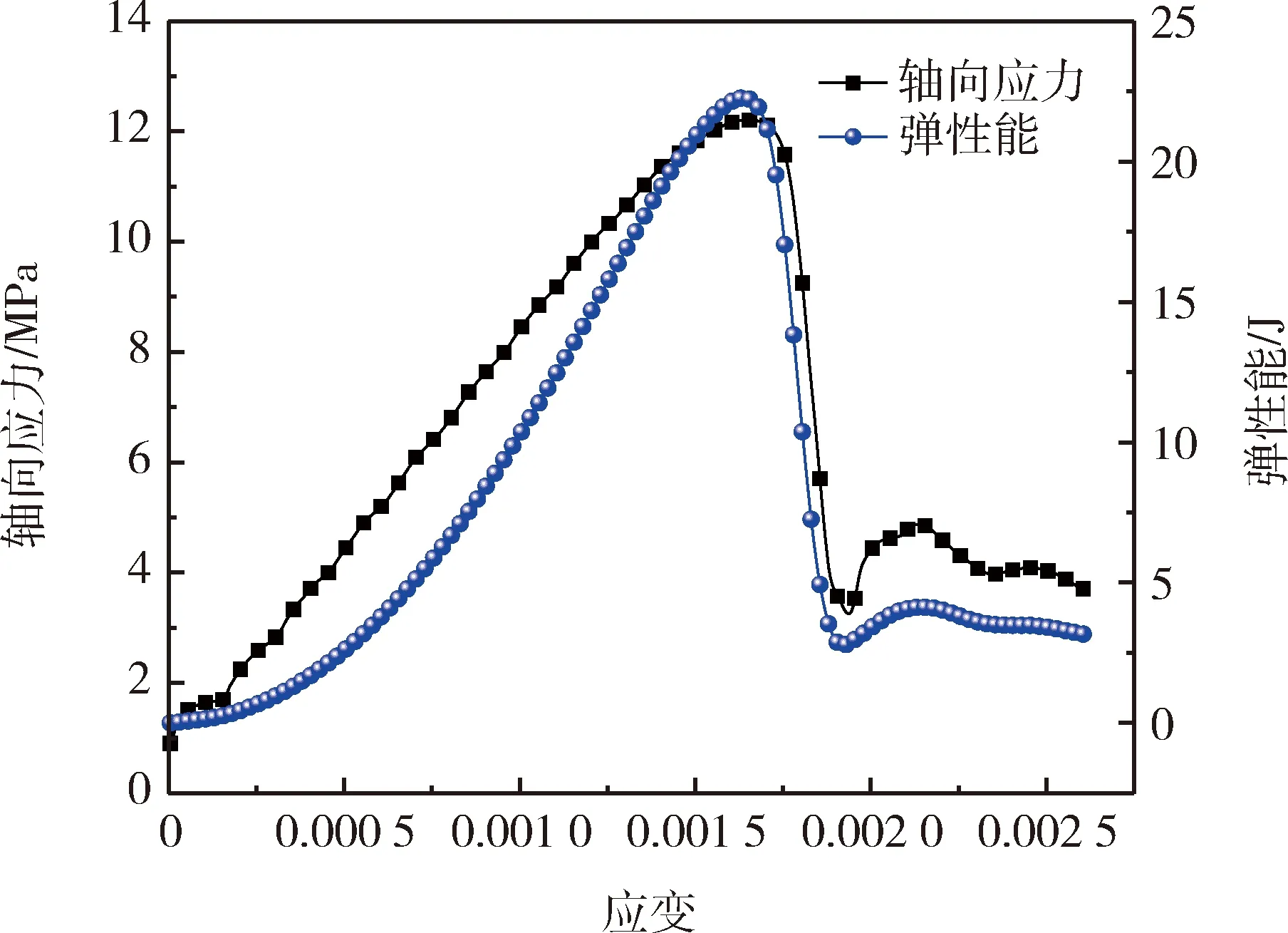
圖6 應力能量曲線Fig.6 Stress energy curve

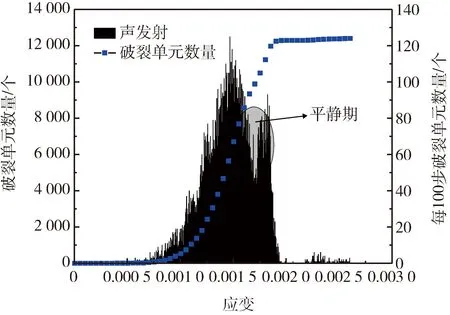
圖7 聲發射曲線Fig.7 Acoustic emission curve

3 討 論

3.1 不同均質度能量演化及聲發射參量

不同均質度條件下巖石應力應變曲線如圖8所示。巖石的彈性模量、峰值強度和均質度呈正相關，即巖石的材料參數分布越統一，高強度材料參數單元數量越多，巖石的宏觀強度越高，這是均質材料無法體現的。同時隨著均質度的增加巖石的脆性程度逐漸增加，表現為峰后階段應力跌落速度越快，這和內部顆粒的膠結程度、顆粒強度有較大關系。均質

圖8 不同均質度應力應變及彈模分布Fig.8 Stress strain and elastic modulus distribution of different homogeneity

度為3、5、7對應的抗壓強度分別為9.43 MPa、11.27 MPa、12.21 MPa，和均質度呈對數函數關系。

從不同均質度單元破壞數量及聲發射參量可以看出，巖石試樣壓縮初始階段，均質度較小的試件已有部分破裂單元，隨著均質度的增大，破裂點出現位置對應應變逐漸增加，表明了高均質材料具有較強的穩定性。但從單元破壞總數量上來看，單元總破壞數量和均質度并無直接關聯。不同均質度對應的聲發射特征差異性較大，均質度較小時，聲發射事件數基本呈n型分布，僅在屈服階段出現小幅度提升；

隨著均質度增大，聲發射事件數分布形態向倒V型轉變(圖9)，即峰前聲發射事件數逐漸增大，到達峰值時突然大幅度提高；隨著均質度增大聲發射頻率及強度表現出不同的形式，這和前人總結的聲發射特征具有高度的一致性，即群震型、前震-主震-余震型和主震型3種典型模式[22]。

圖9 不同均質度單元破壞及聲發射參量Fig.9 Failure and AE parameters of different homogeneity units

3.2 巖石破裂形態描述

為了更好地表征巖石破裂形態，不同學者以不同的思路進行處理，通常我們采用FLAC自帶的塑性區顯示方式，認為巖石進入塑性區即進入破壞狀態，由之帶來的問題則是無法顯示巖石的破裂程度，如果僅從塑性區對某關鍵層位巖層穩定性判定將會帶來誤差，并且相對保守。

本文則通過對比以塑性區、破壞接近度、損傷值(本文定義)等方式對破裂點的描述，分析各種形式的優缺點，以期獲得更合理的表征形式。其中，關于塑性區的定義本文不再贅述，破壞接近度是空間應力的一點沿最不利應力路徑到屈服面的距離與相應的最穩定參考點在相同羅德角方向上沿最不利應力路徑到屈服面的距離之比，見式(6)。

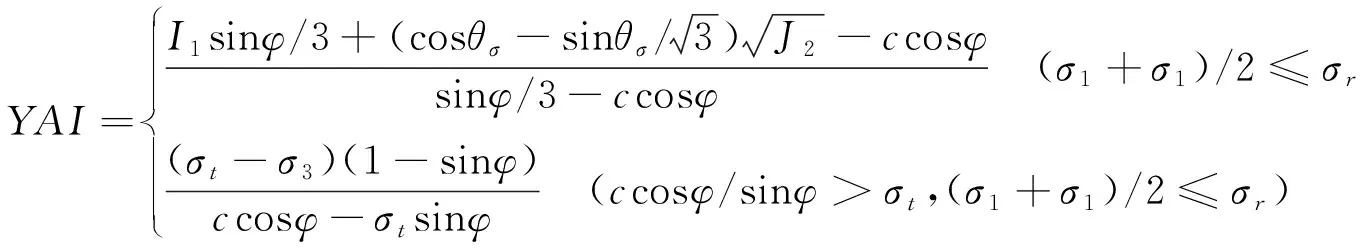
(6)

式中：I1、J2為應力張量的第一不變量、第二不變量；θσ為羅德角。

本文同樣定義了損傷值表達式，已在前文進行說明，不同形式描述巖石破裂特征見圖10。由圖10可知，三者都可以反映出巖石的破裂特征，其中，塑性區表征程度較為一般，它僅反映了巖石破裂點分布，而損傷值則將剪切帶刻畫的更為細致，損傷值為1時表示巖石已完全破壞，不同損傷值表明了巖石所處的應力狀態；損傷值為0時表示巖石處于彈性狀態。破壞接近度則更為細致，它將單元的應力狀態統一起來進行體現，從彈性、塑性、破壞狀態對每個單元的應力狀態進行刻畫，破壞接近度小于1時表明巖石處于彈性狀態，但其彌補了損傷值的不足，即使單元處于彈性狀態，它仍可對較危險單元進行劃分；破壞接近度大于2時表示單元處于破裂狀態，可以根據其值判定巖石較為危險位置。綜上所述，基于破壞接近度的單元接近度評判法則有著較強的優越性。

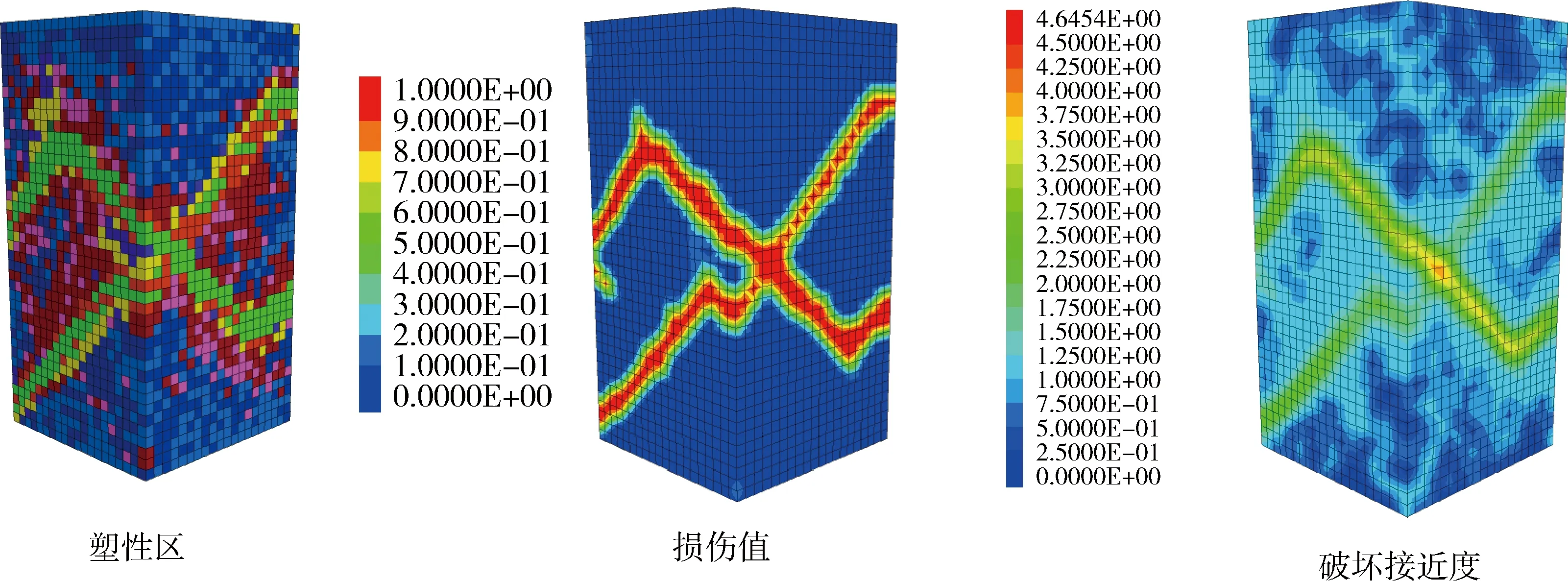
圖10 不同破裂表征形式Fig.10 Different fracture characterization forms

4 結 論

1) 本文建立了非均質巖石應力-損傷本構模型，并采用前人數據驗證了模型的正確性。通過Matlab軟件和FISH語言實現了FLAC非均質巖石單軸壓縮破裂數值計算。

2) 不同均質度單軸壓縮數值計算表明：單軸抗壓強度和彈性模量和均質度呈對數函數關系，隨著均質度系數的增大，巖石由彈塑性向彈脆性演變。

3) 巖石的破裂形態由雜亂無章向局部有序演變，對不同描述破裂特征方式進行了討論，確定了單元破壞接近度的優越性。