Weniger變換在求非諧振子無窮耦合極限中的應用

姚清照， 賀黎明

（華東理工大學物理系，上海 200237）

對許多數學和物理問題進行計算時，經常會得到無窮級數結果。對于一些收斂緩慢或發(fā)散的無窮級數，需要借助特殊的級數計算方法，才能得到有意義的數值結果。近幾十年來，非線性數列變換的方法[1]逐漸發(fā)展，該方法能有效地加速收斂級數以及求發(fā)散級數的和，并在微擾論求解物理體系問題中得到越來越廣泛的應用。

非諧振子是一種重要的物理系統(tǒng)，可以作為晶體振動的簡化模型，且在量子場論中也有廣泛的應用。在用微擾論求解強耦合條件下非諧振子基態(tài)能量本征值時，得到的解是發(fā)散級數，要計算無窮耦合極限必須借助特殊的求級數和技巧。非線性數列變換方法正適合解決這類問題。發(fā)散的級數經過非線性數列變換處理后，可以得到數學性質更好的新數列，從而收斂到一個廣義的極限值（通常稱為反極限），此過程即為發(fā)散級數求和。現有的求解非諧振子問題的工作多數采用浮點計算[2]，所得結果的精度都受到舍入誤差的限制。

本文使用Weniger變換求非諧振子基態(tài)微擾級數和，從而計算四階，六階和八階無窮耦合極限。同時利用計算機代數系統(tǒng)Maple的代數計算功能，進行完全有理化的計算，克服了舍入誤差的限制。針對在計算機代數系統(tǒng)中進行高階Weniger變換時遇到的內存迅速消耗問題，本文采用微擾級數系數分離計算的策略，并壓縮非線性數列變換程序中關鍵數組的維數，通過這兩種優(yōu)化極大地解決了內存溢出的問題，得到精度極高的無窮耦合極限近似值。

1 非諧振子及重整化

諧振子是一種有精確解的物理模型，在許多物理問題中有廣泛的應用。當它處于外場中時，就會產生附加的作用項，此時的體系稱為非諧振子。非諧振子體系沒有嚴格解，只能作近似處理，可以把非諧振子體系的哈密頓量寫成[3]

為了解決微擾級數發(fā)散速度過快的問題，對微擾級數進行重整化處理可以顯著地降低發(fā)散速度，如Arteca等[5]對重整化各種算法進行比較和總結。其中一種方式由Weniger得到[3]，通過引入一對共軛變數：

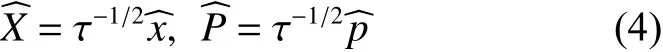
得到了重整化后的哈密頓量

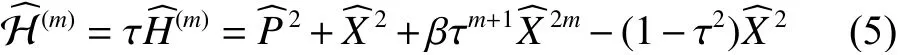
進一步根據變分法并結合其實際的物理意義，就可以得到一個表達式將待定常量 τ 和耦合常數β聯系起來：

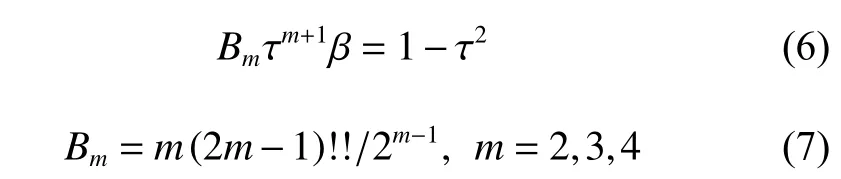
m為2，3，4時分別對應B2=3 ，B3=45/4 ，B4=105/2。引入重整化耦合常數

可得到原哈密頓量中的原耦合常數 β 關于重整化后的耦合常數 κ 的表達式

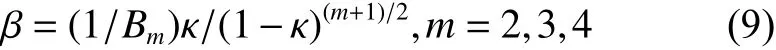
依照式（9）可以得到不同非諧振子體系中耦合常數變換的表達式。原耦合常數 β 符合物理意義的定義域是一個半無窮區(qū)間 [ 0,∞) 。利用式（9），重整化可以將關于 β 的半無窮區(qū)間投影到關于 κ 的左閉右開單位區(qū)間 [ 0,1) 上。重整化方法將耦合常數的定義域重新構造成更小的區(qū)間，從而使發(fā)散微擾級數的求和變得相對簡易，在耦合常數 β 值較大時重整化的優(yōu)勢將尤為明顯。

本文將參量Bm的定義式（7）和新舊耦合常數間的關系式（9）代入重整化哈密頓量表達式中得到更簡約的形式

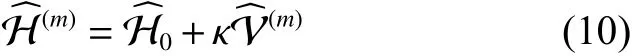
其中

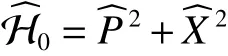
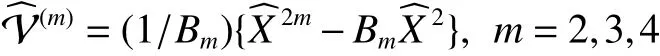
將式（10）帶入Schr?dinger方程則能得到重整化Schr?dinger方程：

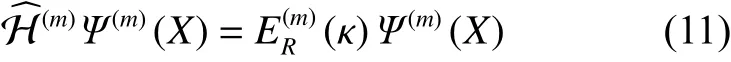
易看出重整化能量本征值(κ) 已由下標R標記出來，此時耦合常數也變?yōu)?κ 。基態(tài)下非諧振子能量本征值

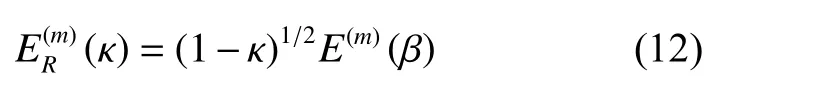
關于 κ 的級數展開為：

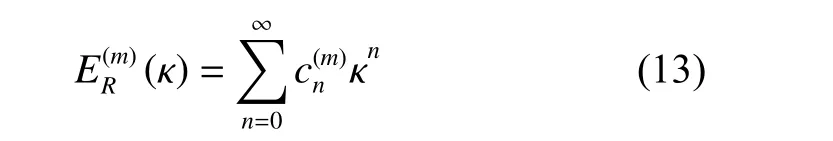
就可以計算出無窮耦合極限km，km的計算式為式（17）。

其中參數Bm的計算式已由式（7）給出。無窮耦合極限km計算所涉及的展開級數是重整化級數中最困難的問題，而有限場強 β 對應耦合常數 κ ∈[0,1) ，此時重整化微擾級數發(fā)散速度相對緩慢，求級數和更為容易。因此，計算無窮耦合極限的工作，對于其他任意有限場強中求解本征值問題有很好的借鑒意義。

我們已知的最好的四階、六階和八階非諧振子的無窮耦合極限結果是由Vinette等[8]通過重整化內投法（Renormalized inner projection）分別計算到小數點后62、33和21位小數。

2 非線性數列變換

非線性數列變換是一種加速級數收斂或求發(fā)散級數和的方法。根據大量的實際計算結果[9-10]可知，Levin變換是效率最高且適用范圍最廣的一種非線性數列變換。然而，在求非諧振子基態(tài)本征值微擾級數和時，Levin變換所得結果出現了發(fā)散的現象，不能計算出高精度的非諧振子無窮耦合極限。考慮到Levin變換通常有很強的求發(fā)散級數和的能力，Weniger在保留Levin變換優(yōu)點的基礎上提出了Weniger變換[1]，該變換是以模型數列式（18）為基礎構造的。

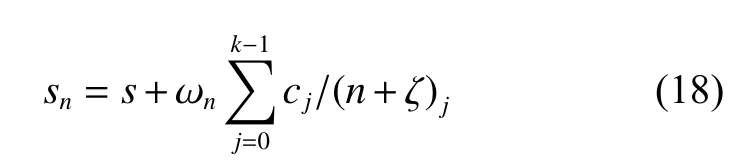
其中 ωn為余項估計，待定參數 ζ =1 ，且式中采用了Pochhammer符號

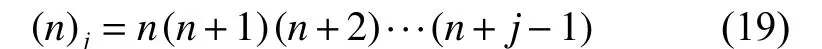
如果式（18）中的余項估計 ωn與部分和之積能作為實際余項rn準確的近似式，那么Weniger變換就能給出高精度的極限s（發(fā)散級數的和通常稱為反極限）近似值。利用差分算符的方法可以得到Weniger變換的定義式為

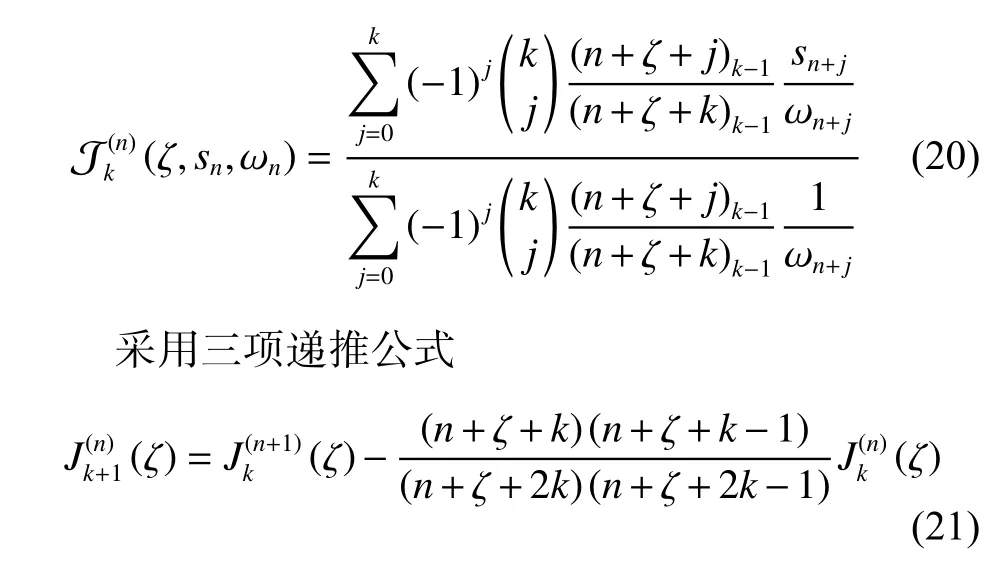
計算式（20）可以看出遞推公式能在Weniger表中形成一個三角形。式中的元素表示定義式（20）中分子或分母的計算值，如果用上標n表示行標，下標k表示列標，則可以構成一個呈左上三角形的二維矩陣：

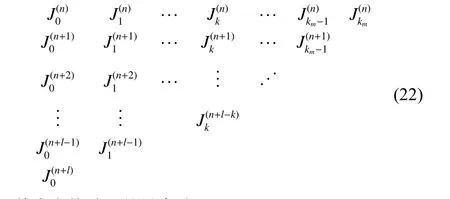
其中變換階k的最高階km=l。

式（22）第1列中的元素是迭代計算過程的起始值，右邊各列的元素都可以通過三項遞推式（21）逐列計算得到。如果用式（23）作為起始值

通過遞推式（21）能得到Weniger變換式（20）的分子。如果用式（24）作為起始值

則計算所得為Weniger變換式（20）的分母。將對應Weniger分子和分母表中相同位置的元素相除，則能得到Weniger變換 J 結果表，其同式（22）一樣是一個左上三角矩陣。

文獻[11]指出，四階、六階和八階非諧振子重整化微擾級數屬于各項正負交替的Stieltjes級數。因此，用余項估計 ωn=?sn=an+1能有效地逼近實際余項，對應得到

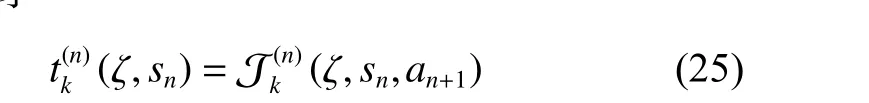
在實際計算過程中，通常以待變數列部分和元素構成的有限子集 {s1,s2,···sl} 作為輸入數據，我們稱這個子集為待變序列。理論上，變換階k增加時產生的結果更精確。然而，在實際計算中，變換結果的精度開始時隨著變換階k的增加而變高，在某一最佳變換階得到有效位數最高的結果后，后續(xù)的結果就會逐漸變差。因此我們需要改變待變序列的長度l，進行多次數列變換，進一步觀察收斂的效果。

本文借助計算機代數系統(tǒng)Maple實現了完全有理化的計算，數據在計算過程始終為有理數格式，所以不會產生舍入誤差，然而，代價是單個數據的表示和計算會消耗更多的內存和機時。隨著計算過程向高階變換進行，Maple會消耗越來越多的內存，因此很容易發(fā)生內存溢出的問題。

針對內存溢出的問題，本文采用了兩種優(yōu)化方案。首先，根據式（14）可以看出，在計算微擾級數系數時需要先計算輔助參數，且隨著n增大輔助參數的個數線性增加。將計算微擾級數系數過程和數列變換迭代過程程序分開，并把微擾級數系數輸出到txt文件中，在計算變換結果前再以有理數格式讀入，這樣則能節(jié)省出可觀的內存。其次，Weniger變換結果表是類似式（22）的三角形二維數組，如果把三項遞推公式（21）計算的結果覆蓋在原參數名上，則能將二維數組壓縮成一維數組，節(jié)省出中間迭代過程消耗的內存。在迭代過程中，每列底部的數據會保持不變，因此我們最后所得一維數組正好是k=0,1,···,km階變換的結果，對應于式（22）矩陣中的反對角矩陣元。

3 計算結果與分析

3.1 四階非諧振子

表1 四階非諧振子微擾級數系數 c (n2) 及其部分和數列∑(n2)Table 1 Coefficients c (n2) and partial sums ∑ (n2) of perturbation series for quartic anharmonic oscillator

表2 四階非諧振子微擾級數系數 及其部分和數列的浮點數計算結果Table 2Floating-type coefficients and partial sums of perturbation series for quartic anharmonic oscillator

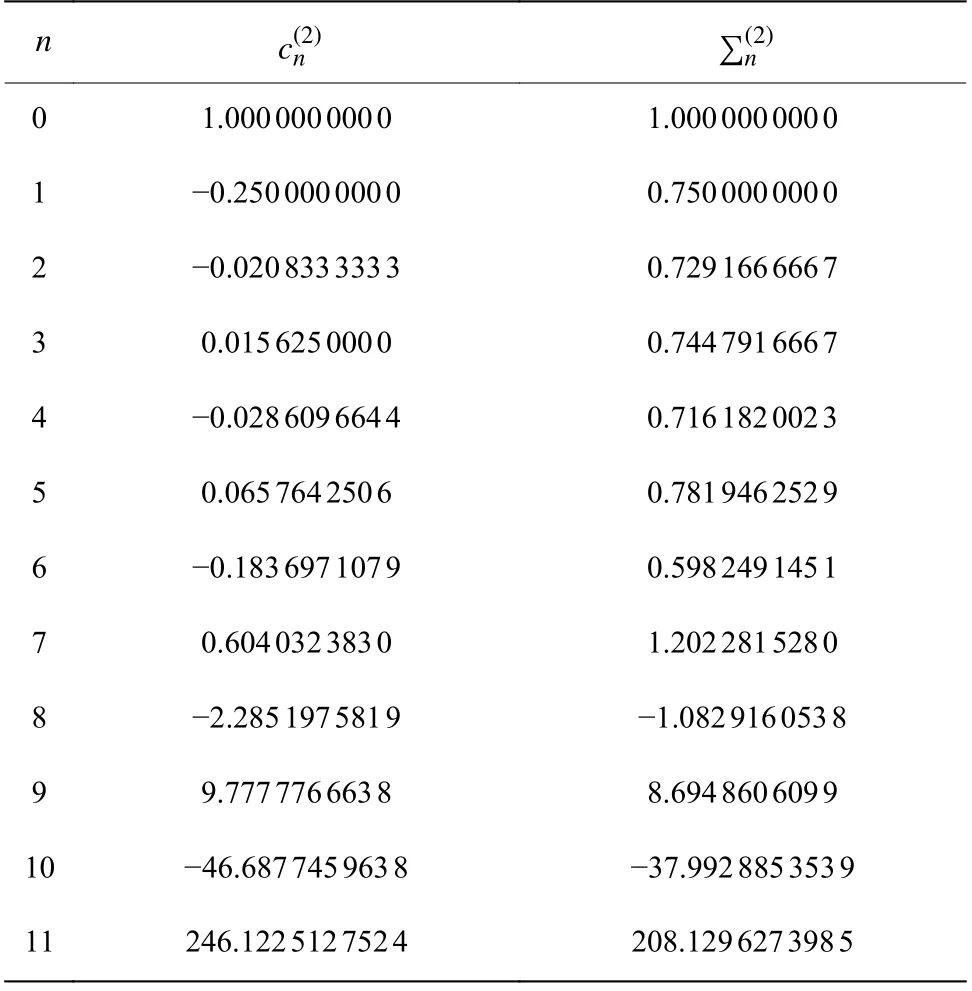
表2 四階非諧振子微擾級數系數 及其部分和數列的浮點數計算結果Table 2Floating-type coefficients and partial sums of perturbation series for quartic anharmonic oscillator

n c(2)n∑(2)n 1.000 000 000 0 1.000 000 000 0 1?0.250 000 000 0 0.750 000 000 0 2?0.020 833 333 3 0.729 166 666 7 3 0.015 625 000 0 0.744 791 666 7 4?0.028 609 664 4 0.716 182 002 3 5 0.065 764 250 6 0.781 946 252 9 6?0.183 697 107 9 0.598 249 145 1 7 0.604 032 383 0 1.202 281 528 0 8?2.285 197 581 9 ?1.082 916 053 8 9 9.777 776 663 8 8.694 860 609 9 10 ?46.687 745 963 8 ?37.992 885 353 9 11 246.122 512 752 4 208.129 627 398 5 0

計算結果列于表3第2列。由表3可以看出，無窮耦合極限k2的吻合的有效位數開始時隨著變換階k的增加而變多，到了第7階后有效位數又開始減少。

為了更定量且直觀地考察Weniger變換過程的收斂情況，定義：

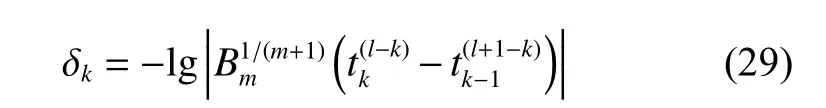
δk表示相鄰兩次迭代結果的符合程度，大致對應于兩個十進制浮點數取得一致的位數。不同變換階k時計算結果的 δk不同，通常 δk值越大對應的近似值精度也就越高。從表3可以看出，通過數列變換的方法，我們從發(fā)散級數所包含的數學信息中提取出了收斂的有限值，原本發(fā)散的微擾級數因此獲得了物理意義。 δk先隨著變換階k的增加而不斷增加，在最佳變換階k=7 時最大，然后轉為變小。因此最高精度為 ?10=6.947 ，對應收斂到7位有效數字的結果為k2=1.060361 。

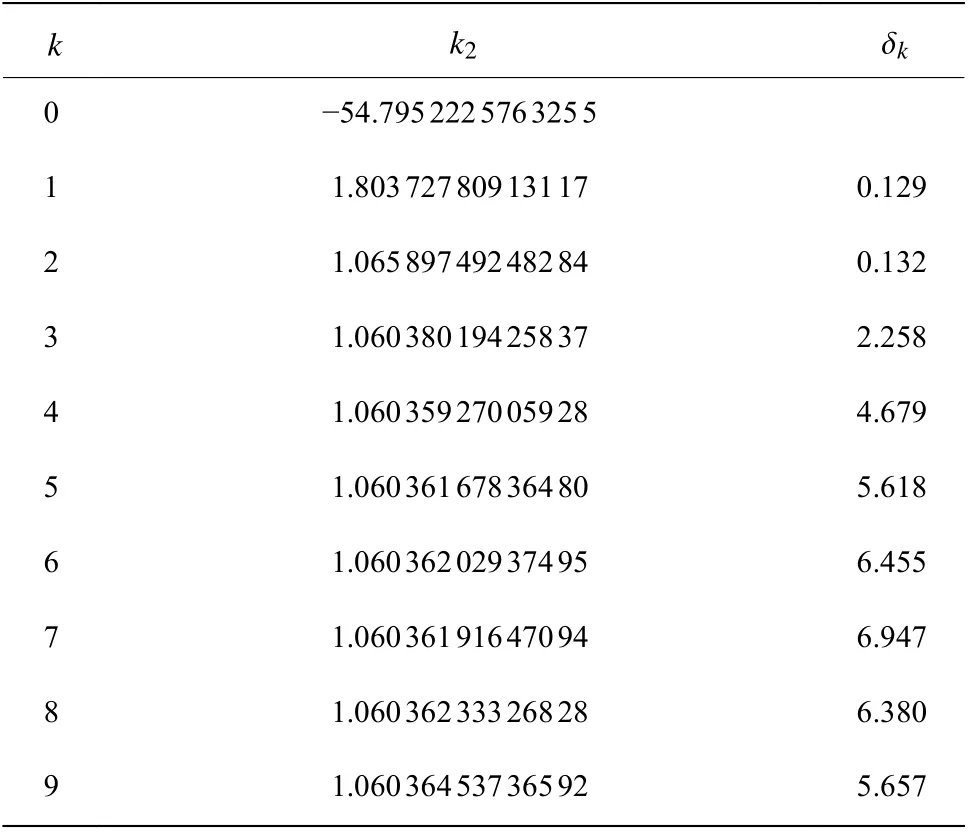
表3 序列（27）Weniger變換的結果Table 3 Numerical results of Weniger transformation for the string (27)

為了更深入地考查Weniger變換求四階非諧振子微擾級數和的能力，按照與l=100 時相同的方法，依次計算了待變序列長度l=200,300,···,800 的Weniger變換結果，整理成表5。計算Weniger變換所選擇的待變序列越長，所需要的微擾級數系數越多，可以進行更高階的變換，給出的結果精度越高，最高精度 ?l=105.646 ，是由待變序列長度l=800變換到k=756 得到k2為1.060 362 090 484 182 899 647 046 016 692 663 545 515 208 728 528 977 933 216 245 241 695 943 563 044 344 421 126 896 299 134 671703 510 546，這比現有的最準確的內投法結果[8]還要高出大約43位有效數字。

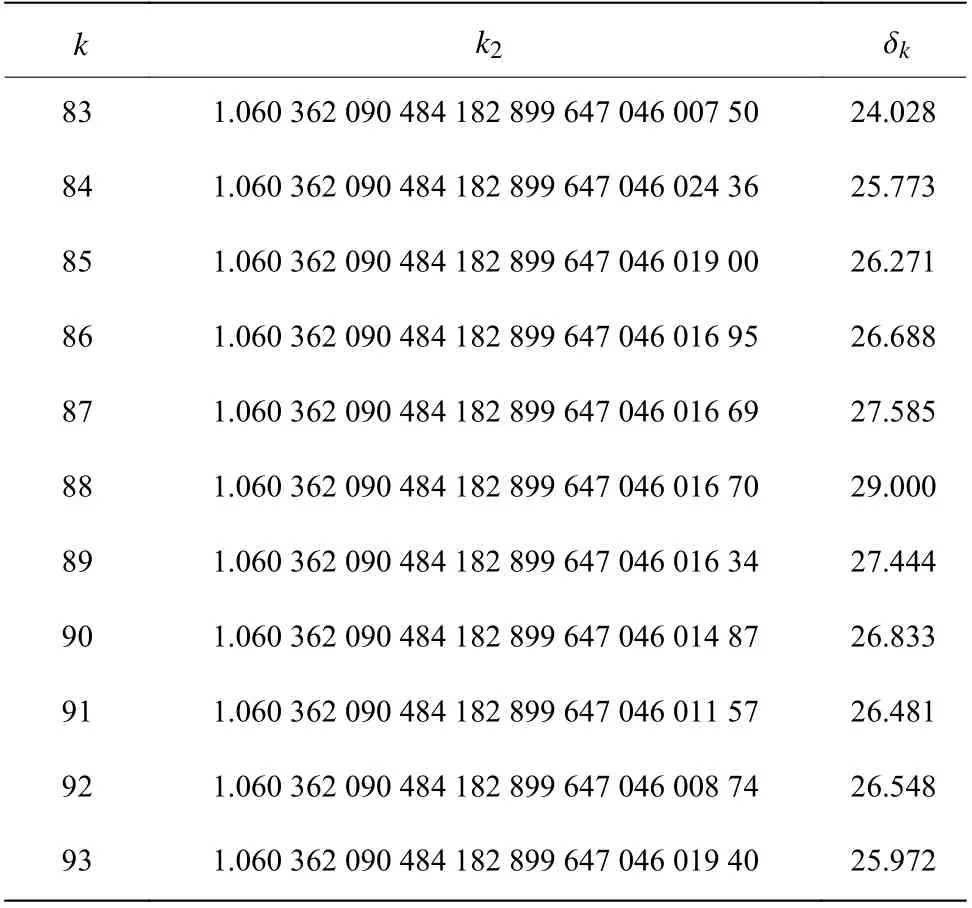
表4 l為100時Weniger變換的結果Table 4 Numerical results of Weniger transformation for l=100

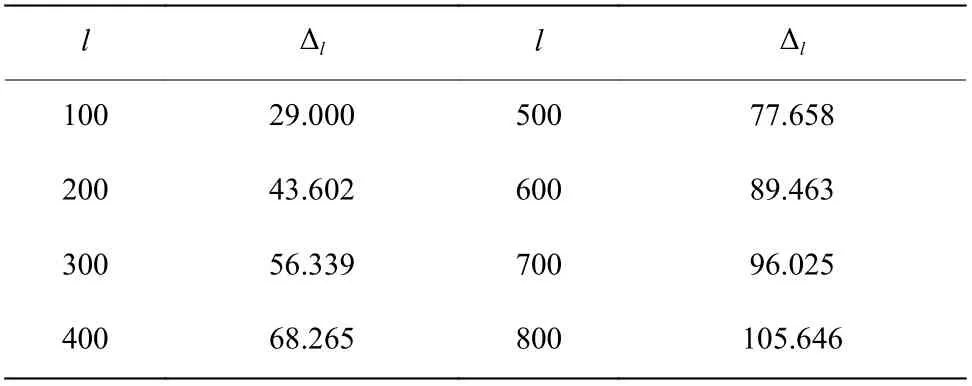
表5 對不同長度l待變序列式（27）進行Weniger變換得到無窮耦合極限 k2 的有效位數?lTable 5 Number of decimal significant digits ?l of approximations of infinite coupling limit k2 given by Weniger transformation for various lengths of strings(27)

本文使用圖形軟件Origin，以擬合函數?l=a+bl+cl2對表5中的 ?l和l數據進行二次多項式擬合，可以得到圖1。其中，截距a=14.56107± 1 .31521 ，一階系數b=0.15349±0.00671 ，二階系數c=?5.0519×10?5±7.27312×10?6，殘 差 平 方 和 為 4 .44345 ，R2=0.9991 。從圖1可以看出吻合的有效數字位數 ?l關于待變序列長度l線性增加，這說明我們只需增加待變序列長度就可以計算出有效數字更多的四階非諧振子耦合極限k2。

3.2 六階非諧振子

六階非諧振子微擾級數系數增長更迅速，文獻[3]中，在指標n相同時微擾系數相對于四階非諧振子的系數更大，微擾級數發(fā)散更快。因此待變序列式（27）的長度相同時，六階非諧振子的計算量更大。依照四階非諧振子的情形，我們使用Weniger變

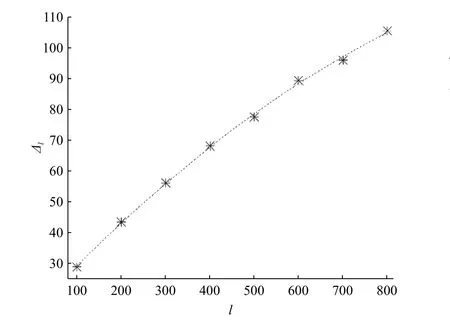
圖1 四階非諧振子無窮耦合極限 k2 近似值的有效位數?l 與待變序列式（27）長度 l 之間的關系Fig. 1 Relationship between the significant digit ?l of the approximation k2 of the infinite coupling limit of the quartic nonharmonic oscillator and the length l of the string (27)

3.3 八階非諧振子

以長度l=100 待變序列式（27）經過Weniger變換所得八階非諧振子無窮耦合極限k4，結果如表8所示。結合表4、表6和表8可得，四階、六階和八階非諧振子在待變序列長度l=100 時，有效位數?l逐漸減少，依次為29，11和6。對于同樣長度的待變序列，由于級數的發(fā)散特性更加明顯，m值大階數高的非諧振子需要消耗更大的計算量和內存空間，卻只能得到更差的結果。

我們依次對長度l=200,300,···,900 的待變序列式（27）進行了Weniger變換。在待變序列長度l＞500后，出現了服務器內存溢出的問題。我們通過優(yōu)化數組結構等方法，成功計算出了待變序列長度l=900 時八階非諧振子的無窮耦合極限，結果見表9。從表9可以看出變換階k=890 時得到最高有效位數 ?900= 1 3.488 ，即第890階變換結果和第889階變換結果大致有14位吻合的有效數字，這時已到達我們計算資源的極限。

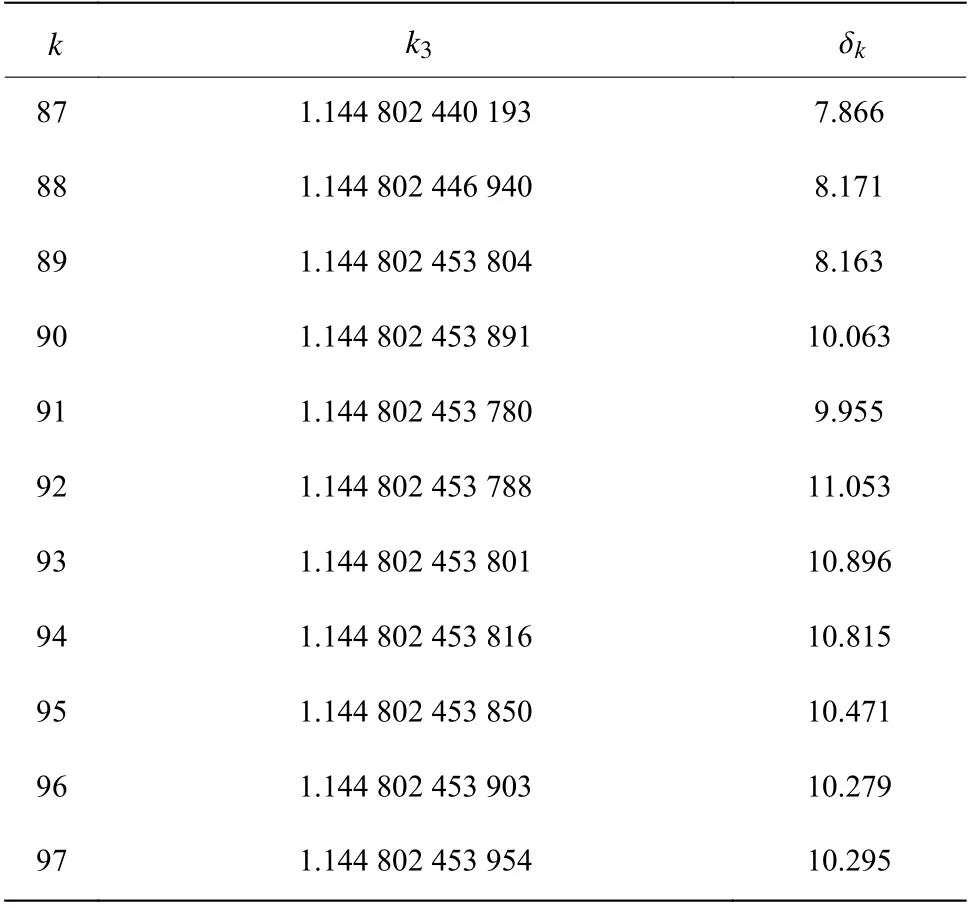
表6 l =100 時Weniger變換的結果Table 6 Numerical results of Weniger transformation for l=100

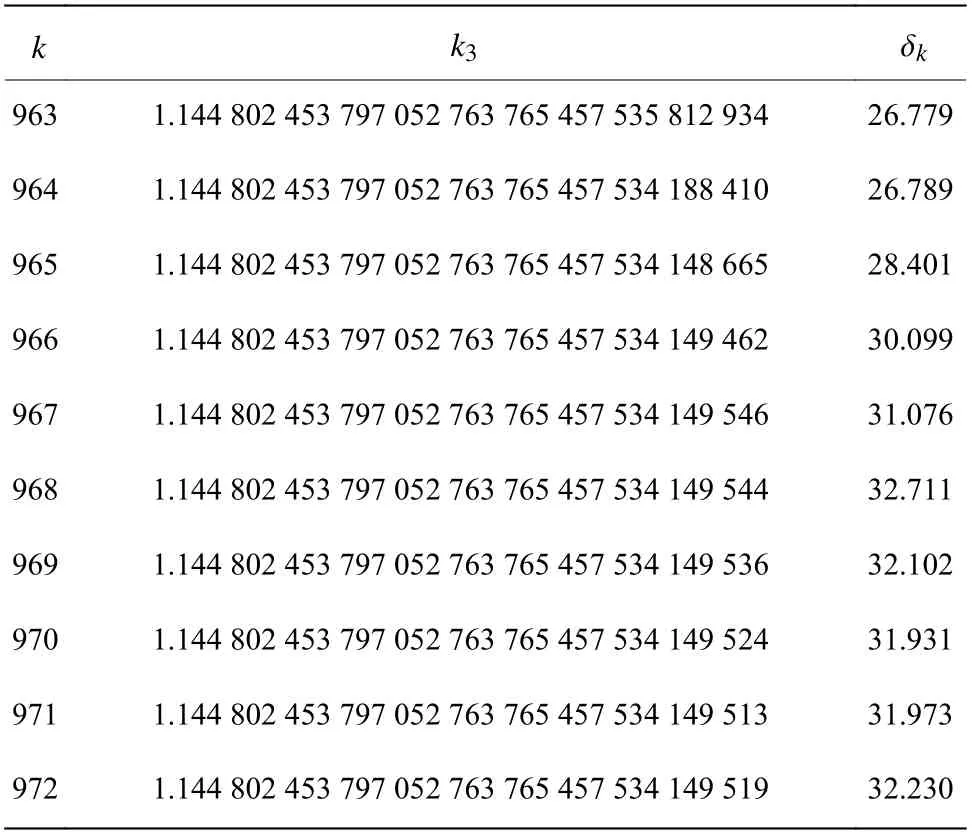
表7 l =1000 時Weniger變換的結果Table 7 Numerical results of Weniger transformation for l=1000

4 結論與展望

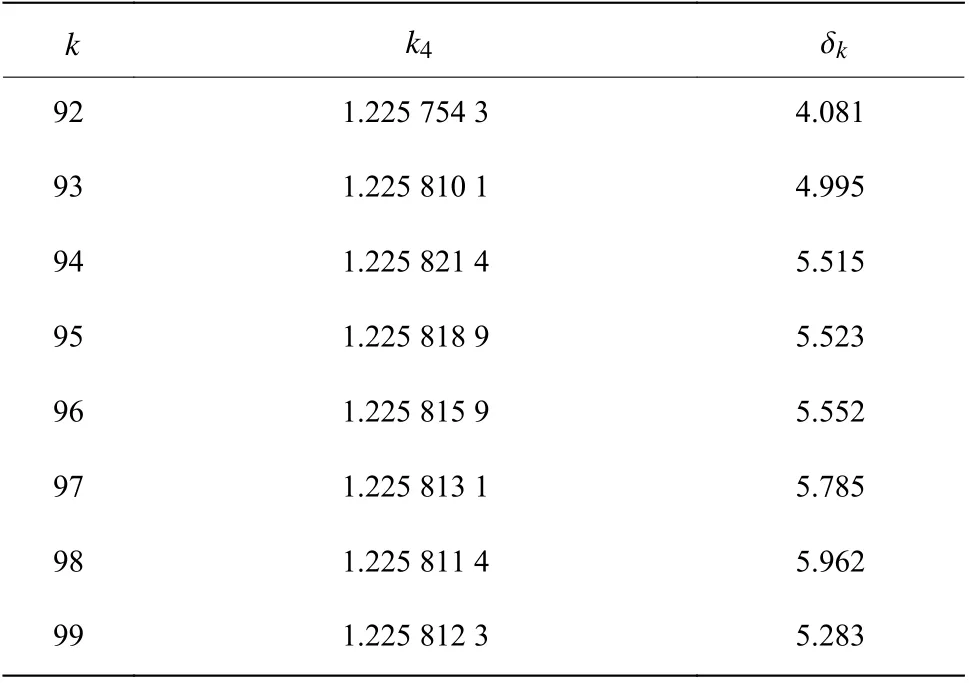
表8 l =100 時Weniger變換的結果Table 8 Numerical results of Weniger transformation for l=100

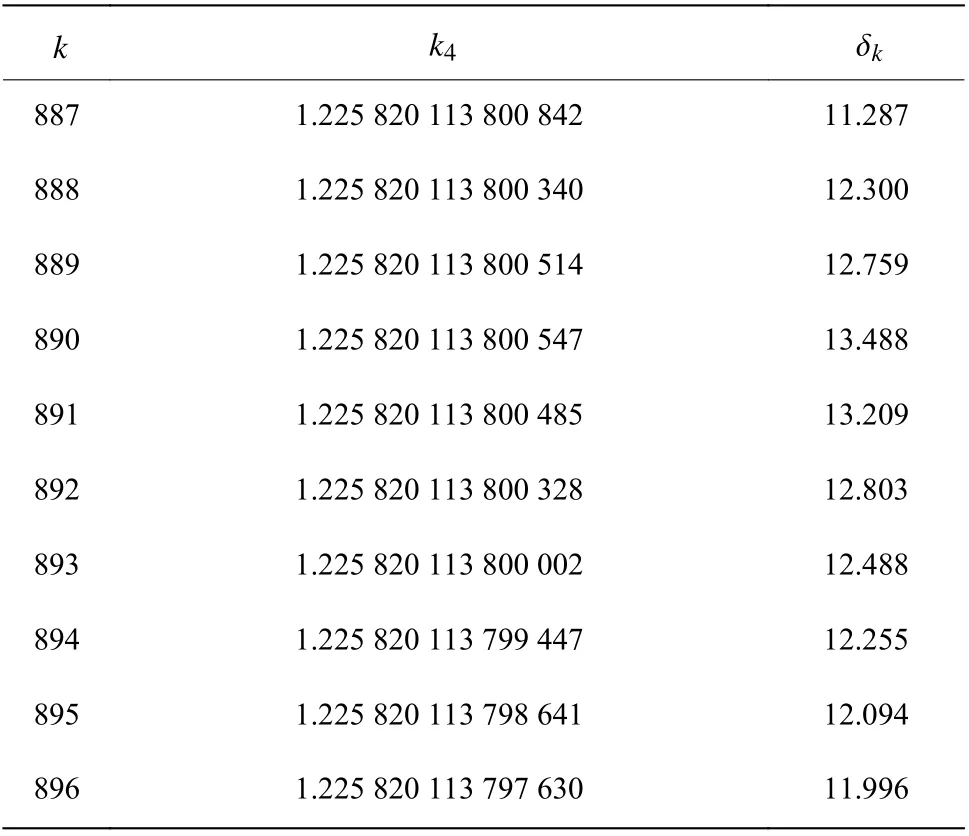
表9 l =900 時Weniger變換的結果Table 9 Numerical results of Weniger transformation for l=900

在Maple計算過程中，每個系數是巨大的有理分數形式，不僅占據了大量內存，還會明顯增加計算量。六階和八階非諧振子微擾級數系數比四階的增長更快，在進行Weniger變換時需要更多的內存和計算量，計算無窮耦合極限也就更為困難。我們計算無窮耦合極限k3和k4時遇到了服務器內存溢出的問題，為此我們改進了Weniger的程序數組結構，將二維數組通過覆蓋的編程技巧將其壓縮為一維數組。一維數組的優(yōu)化方案節(jié)省了巨大的內存，這個改進使我們可以計算出比Weniger更準確的結果，不然的話，即使是在我們現有的計算條件下也很難得出比Weniger[3]更好的計算結果。此外，由公式（14）可以看出，將計算微擾級數系數c(nm)部分的程序分離出迭代的變換過程，也能節(jié)省出大量保存輔助參數時被浪費的內存。微擾級數的微擾階越高，待變序列長度越長，這種優(yōu)化方案的優(yōu)勢就更顯著。表10中匯總了我們優(yōu)化方案的計算結果和其他方法所得結果的比較。

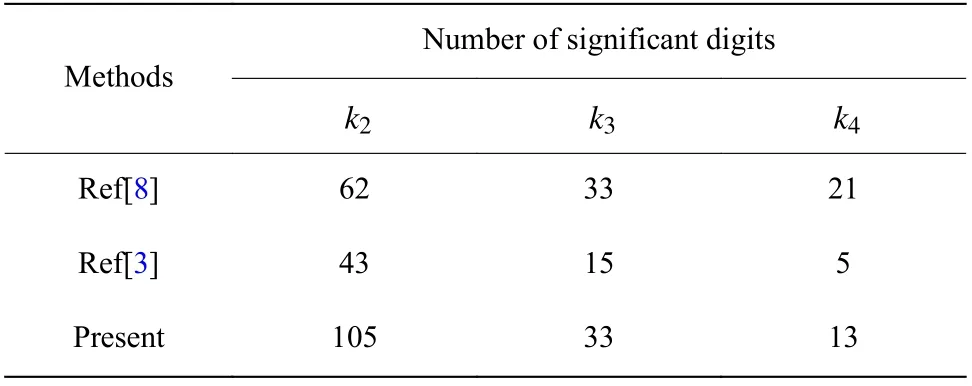
表10 四階、六階和八階無窮耦合極限計算結果與其他方法的比較Table 10 Comparison between present numerical results of quartic, sextic and octic infinite coupling limits and other methods

如果有更多的計算機內存資源，則可以計算出更多位數的無窮耦合極限。而且當內存足夠充足時，若使用Maple的并行運算功能，將極大地提升計算速度，節(jié)省CPU時間。因此內存資源是更為關鍵因素。

微擾論是求解許多物理體系的常用近似計算方法。實際計算得到的無窮級數為緩慢收斂和發(fā)散的情況也是非常普遍的。于是，通過非線性數列變換改善無窮級數的收斂性質具有普遍的實際意義[12]。