高精度有限差分格式的色散優化及耗散控制

李妍慧, 陳琮巍, 任玉新,*, 孫振生, 王秋菊

(1. 清華大學 航天航空學院, 北京 100084; 2. 火箭軍工程大學, 西安 710025; 3. 北京應用物理與計算數學研究所, 北京 100094)

0 引 言

超聲速流中，多尺度結構(如湍流)、間斷(如激波)以及這些結構之間的相互作用同時存在，給數值模擬帶來很大的挑戰。一方面，多尺度結構要求數值格式具有較小的色散耗散誤差以精確地捕捉幅值和相位，另一方面，間斷附近需要格式具有足夠的耗散以抑制數值振蕩。這兩種矛盾的要求使得構造高分辨率的激波捕捉格式非常困難。目前最具代表性的高精度激波捕捉格式是WENO格式，它最初由Liu等[1]提出，之后被Jiang和Shu[2]改進。WENO格式可以根據流場局部的光滑性，動態調整候選模板的權重來無振蕩地捕捉激波，但是這一非線性機制也使得格式在光滑區的耗散過大，特別是在計算可壓縮流動的多尺度結構時，數值耗散可能會高于物理耗散[3]。

解決這一問題的一種方法是改進WENO或ENO格式的非線性機制，更好地實現光滑區和間斷的尺度分離。Henrick等[4]提出了WENO-M格式，通過映射非線性權解決了WENO-JS在極點處不滿足五階收斂條件的問題。Borgers等[5]提出的WENO-Z格式采用了一種歸一化的光滑因子，可以使非線性權在光滑區更快地恢復到線性權。該格式在極點處也滿足五階收斂條件，且計算量遠小于WENO-M格式。劉朋欣等[6]參考Henrick等[4]提出的映射函數的思想，將一種五次分段多項式映射函數應用于一種由NND格式改型得到的中心型三階格式，構造出SWENO3-PPM5格式，算例測試結果表明該格式具有比WENO3更高的分辨率。Taylor等[7]基于一種相對光滑限制器構造得到WENO-RL格式，當光滑因子間的比值較小時直接采用線性權，這種方法可以使格式在中低波數段的色散耗散特性和對應的線性格式一致，從而改善格式的譜特性。WENO-SYMBO格式[8]將對應的線性格式由迎風改為中心格式，并通過求解一個積分形式目標函數的最小值，對格式的譜特性進行優化。Hu和Adams等[9]發展了一種自適應的中心迎風六階WENO格式(WENO-CU6)，采用新的光滑因子控制格式在中心和迎風之間切換。最近發展的TENO格式[10]采用新的模板選擇和加權策略，來實現光滑區和間斷的有效區分，從而改善分辨率。

另外一種方法是利用間斷探測器，將激波捕捉格式和譜特性良好的格式結合起來，構造混合格式。混合格式在流場光滑區采用低耗散的格式以提高分辨率，而在間斷附近采用激波捕捉格式以避免數值振蕩。混合格式首先由Adams和Shariff[11]提出，他們將非守恒形式的緊致格式與ENO格式相結合，用于激波湍流相互作用流場的模擬。Pirozzoli[12]將守恒的緊致格式與WENO格式相結合，構造了一種守恒的緊致-WENO混合格式。該工作由Ren等[13]進一步發展，他設計了一種新的間斷探測器，并采用加權的方式將守恒的緊致格式和WENO格式混合，避免了兩種格式的突然切換。武從海等[14]將Ren等[13]提出的間斷探測器進行改進，構造了基于WENO-Z格式和五階守恒緊致格式的混合格式，并且通過僅對混合格式中WENO部分進行特征投影處理，提高了計算效率。對于混合格式，間斷探測器的精度對格式的譜特性有很大影響。傳統的間斷探測器通常采用流場解的一階導數或二階導數來判斷流場的光滑性[13,15-16]。此外，近年來還發展了基于非正交小波基函數[15,17]以及WENO非線性權[18-21]的間斷探測器。然而，如何將間斷和高頻成分以及極點進行區分仍然是一個困難的問題。

上述兩種方法改善計算效果的主要思路都是在流場光滑區盡可能地優先采用線性格式，因此，線性格式的性能對最終計算結果有直接影響。例如，WENO-M和WENO-Z等的線性格式是五階迎風格式，而WENO-SYMBO格式對應的線性格式是六階中心格式。混合格式的線性部分則多采用緊致格式和中心格式。當線性格式是迎風格式時，對湍流直接數值模擬等應用而言，耗散還是較大；當線性格式為中心格式時，耗散則不足。Pirozzoli[12]指出，為了減少數值振蕩，格式需要具有一定的耗散以抑制色散誤差較大的高波數成分。但是，如何合理地確定線性格式的耗散大小仍然是一個開放問題。

我們最近的工作，就是解決混合格式中線性部分的色散優化和耗散控制問題。關于色散優化的方法，已經開展了較多研究，但是線性格式的耗散控制相關的研究還比較少。本文綜述了我們近期的相關研究工作。首先，Sun等[22]提出了一類色散耗散相互獨立的有限差分格式，在優化色散同時，耗散可以通過一個參數調節，從而得到了色散最小、耗散可控(Minimized Dispersion and Controllable Dissipation, MDCD)格式。但是MDCD格式耗散參數的設置依賴于具體問題，需要基于經驗人工進行選取，而在大型的數值計算如直接數值模擬中，參數的調試會花費大量的時間。Hu等[23]認為，格式的耗散大小應該與色散誤差相關。他們據此得到一個色散耗散條件，來確定足夠的耗散以抑制非物理的高頻振蕩。Sun等[24]根據這一關系，確定了六階MDCD格式的耗散參數，在多個測試算例中，格式均表現出較好的魯棒性。這種方法雖然可以得到具有合適耗散的格式，但它只能調節格式耗散的整體水平，而沒有考慮解的局部尺度。

理想的格式耗散應該是與數值解的局部尺度相關的。在解的局部尺度遠大于網格尺度時，線性格式的耗散應該很小甚至為0。當解的局部尺度與網格尺度接近時，此時格式的色散誤差已非常大，應當將耗散增加到足以抑制高波數振蕩的水平。根據這一思想，Li等[25]發展了一類具有最小色散、自適應耗散特性(Minimized Dispersion and Adaptive Dissipation, MDAD)的格式。

自適應耗散的差分格式包含以下要素。首先，為了保證耗散的自適應不影響格式的色散特性，選擇色散和耗散相互獨立的四階MDCD格式作為自適應耗散格式的基礎。其次，為了識別數值解的局部尺度，Li等[25]提出了一種基于流場解的導數的尺度識別器，可用來得到數值解局部的等效無量綱波數。最后，采用Hu等[23]提出的色散耗散條件，設計出耗散參數與局部等效無量綱波數之間的關系，從而構造得到具有自適應耗散特性的MDAD格式。

為了使格式具有激波捕捉能力，通過將MDAD格式的數值通量表示為一系列候選模板上的低階多項式的線性組合，并引入WENO格式的非線性權，發展了MDAD-WENO格式。之后將MDAD格式與MDAD-WENO格式相結合，構造了一種混合格式，記為MDAD-HY。采用近似色散關系[26]分析MDAD-HY格式與其他激波捕捉格式的近似譜特性，發現MDAD-HY格式相比基于MDCD的混合格式MDCD-HY，在中低波數段的耗散更小，而在高波數段有相近的耗散，說明格式在數值解尺度較大的區域分辨率較高，而在間斷區也有較好的魯棒性。構造混合格式的一個關鍵問題是合理的間斷探測器。為此，Li等[25]將傳統間斷探測器[13]與尺度識別器相結合，提出了一種新的間斷探測器，能夠有效減少對光滑區的極點的誤判。

本文介紹了MDCD格式、MDAD格式、混合格式MDCD-HY和MDAD-HY，以及MDCD格式的應用情況和MDAD格式的測試算例，最后作出了總結。

1 色散最小、耗散可控有限差分格式

本文以一維線性波動方程為例，介紹高精度有限差分格式的色散優化和耗散控制方法。方程形式如下:

其中,u為守恒量，f=au為通量且a為常數。考慮在均勻網格上，采用半離散有限差分格式對式(1)在(xj,t)處進行離散，得到:

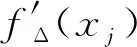
其中fj+m=f(xj+mΔx)。式(3)可改寫為守恒形式，即:

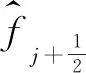
常規的數值格式色散和耗散特性是相互關聯的，但是MDCD格式具有色散、耗散相互獨立的特性，這就使得它可以對色散進行單獨優化，而耗散也可以根據不同工況進行調節。為了簡潔，本文將只介紹四階MDCD格式[22]，六階MDCD格式的具體細節參見文獻[24]。

1.1 MDCD格式的半離散特性

當空間有限差分格式包含對稱的(2r+1)個模板點時，式(3)可寫為:

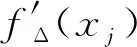
當r=3時，四階的MDCD格式[22]形式如下：

不論γdisp和γdiss如何選取，格式都有四階精度。

下面分析式(6)所示四階MDCD的半離散色散耗散特性。考慮單一的簡諧波，

則空間一階偏導數有精確解

其中k=ωΔx為無量綱波數。將式(8)代入式(6)并寫為：

其中k′=R(k′)+iI(k′)為修正的無量綱波數，R(k′)和I(k′)為k′的實部和虛部，分別控制半離散格式的色散和耗散特性。則四階MDCD格式的半離散色散和耗散特性為:

I(k′)=γdiss(cos3k-6cos2k+15cosk-10)

(11)

顯然格式的色散特性只與γdisp有關，耗散特性只與γdiss有關，從而實現了對格式色散和耗散的單獨控制。

MDCD格式的色散和耗散特性是相互獨立的，因此可以對色散進行單獨優化而不影響耗散。通常認為格式的色散誤差應當在選定的標準下達到最小。文獻[8]設計了一種加權積分形式的優化目標函數:

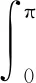
(12)

其中e-νk用于控制不同波數下色散誤差的相對權重，通過求解使目標函數式(12)最小的優化問題，可以得到最優的色散參數γdisp。為了使格式在盡可能大的波數范圍內都有較小的色散誤差，文獻[22]最終采用了ν=8下的最優色散參數,

γdisp=0.046 378 3

(13)

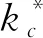
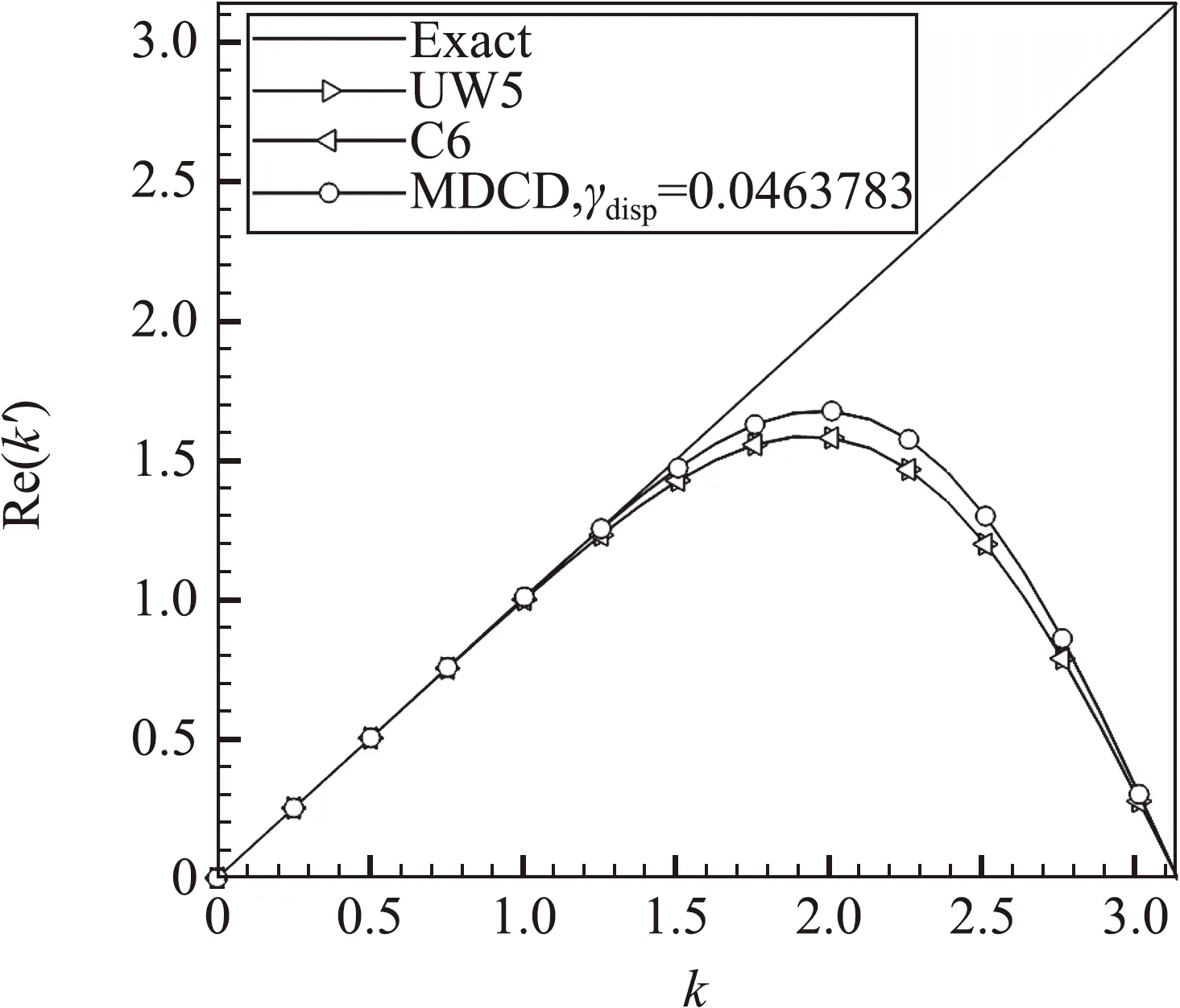
圖1 不同格式的色散特性

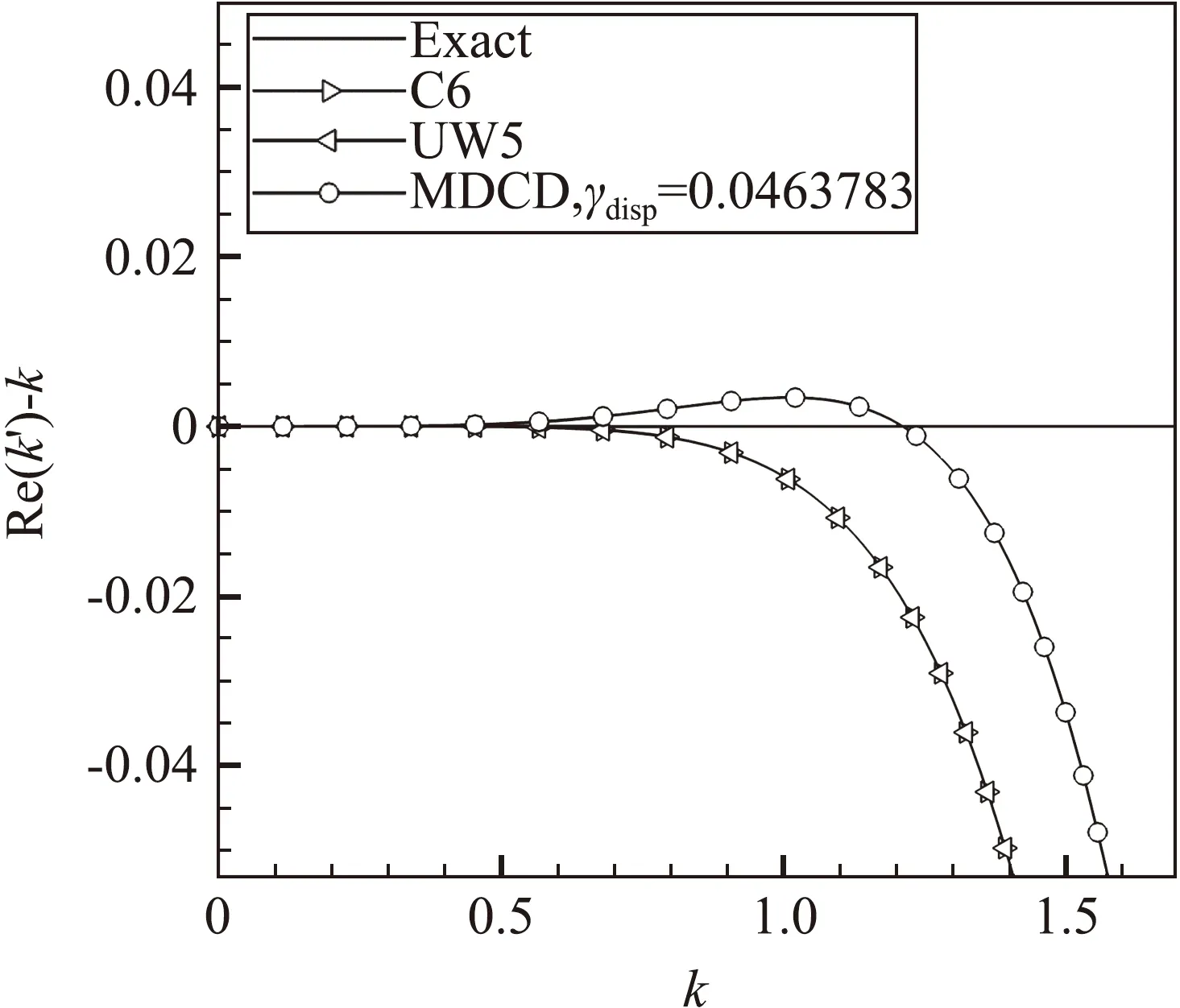
圖2 不同格式的色散誤差

對于耗散特性，為了使格式保持穩定，所有波數下的耗散都應非負。由式(11)所示，MDCD格式的耗散大小只與γdiss有關，虛部I(k′)可改寫為:

I(k′)=γdissg(cosk)

(14)

其中,

g(x)=4x3-12x2+12x-4

(15)

由于g′(x)=12(x-1)2≥0，為單調非減函數，易證g(cosk)≤0。因此當a>0時，如果γdiss≥0，則MDCD格式有非負耗散，格式是穩定的，且隨著γdiss的增大，格式的耗散增加。當耗散參數取0時，MDCD為中心格式，此時格式分辨率最高，但是無法抑制高波數的非物理振蕩。

在實際計算中，正如文獻[12]提到的，格式需要具有一定的耗散。對于四階MDCD格式，Sun等[22]對不同算例采用試錯的方法確定合適的耗散參數γdiss進行計算。而在文獻[24]中，Sun等采用Hu等[23]提出的色散耗散條件確定了六階MDCD格式的耗散參數。多個數值實驗結果顯示該六階MDCD格式表現出較好的魯棒性，沒有出現明顯的數值振蕩。Hu等[23]提出的色散耗散條件具體形式如下:

Hu等認為格式的耗散應當與色散誤差相關，在式(16)中，給定波數下的色散耗散比值r越小表示格式對該波數的波耗散越大。當r<10時，格式的耗散基本可以抑制非物理的高頻波動。這里我們采用與文獻[24]相同的做法確定四階MDCD格式的通用耗散參數γdiss。考慮到k=π時格式的耗散最大，我們采用r(π)來確定γdiss。本文選擇r≤9作為限制條件，此時滿足條件的最小耗散參數為：

γdiss=0.012

(17)

圖3展示了不同耗散參數下的MDCD格式與UW5以及C6格式的半離散耗散特性對比，其中括號內的數字為耗散參數的大小。可以看到C6和MDCD(0)均為零耗散，MDCD(0.035)的耗散特性與UW5接近，而MDCD(0.012)的耗散介于C6和UW5之間。MDCD(0.012)在中低波數段耗散較小，格式有較高的分辨率，在高波數段，格式的色散誤差變大時，也能提供足夠的耗散來抑制振蕩，有較好的魯棒性。因此，對于大多數工況，我們推薦采用MDCD(0.012)。在本文中，如無特殊說明，MDCD格式的耗散參數均采用γdiss=0.012。

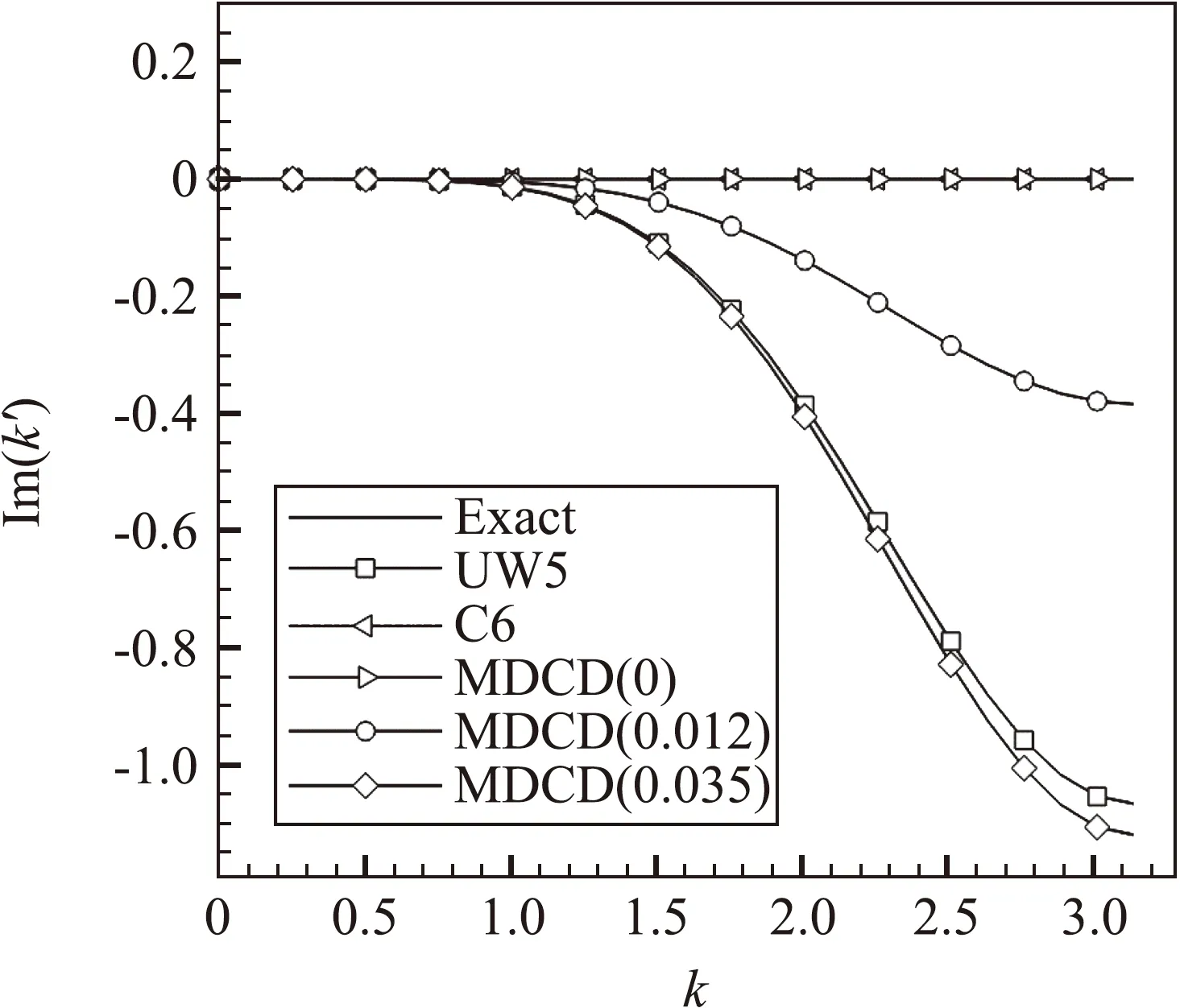
圖3 不同格式的耗散特性

1.2 MDCD格式的全離散特性分析

上一節中我們提到，MDCD格式的半離散色散耗散特性相互獨立，分別受色散參數γdisp和耗散參數γdiss控制。但實際計算中，結果同時受到空間離散和時間離散的影響，因此分析格式的全離散特性是有必要的。

考慮線性對流方程：

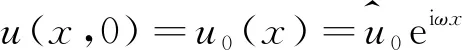
其中c=aΔt/Δx為庫朗數，k=ωΔx為無量綱波數。而半離散方程式(4)的解為：

其中k′為1.1節中所述的無量綱修正波數。對比式(19)和式(20)，可以發現空間離散格式引入的誤差為：

rs=e-i(k′-k)c=eI(k′)ce-i(R(k′)-k)c

(21)

其中|rs|=eI(k′)c為半離散耗散誤差，而δs=(R(k′)-k)c為半離散色散誤差。若采用顯式龍格庫塔格式進行時間積分，則在t=Δt時刻有：

其中G(k,c)為放大因子，具體形式為一個s階多項式，其中s為龍格庫塔格式的級數。對比式(22)和式(19)，可以發現G(k,c)為精確的放大因子e-ikc的近似。因此，格式的全離散誤差為：

其中|rt|=|G(k,c)|為全離散耗散誤差，δt=-δG-kc為全離散色散誤差。考慮到1.1節中分析半離散色散耗散特性時采用的是R(k′)和I(k′)，為了使全離散特性分析與半離散量級一致，對比|rs|和|rt|，以及δs和δt，我們得到：

其中kt為全離散情況下的等效無量綱修正波數。由式(24)可知，全離散的色散耗散特性均與庫朗數c有關。為了不失一般性，我們采用c=0.3、0.6、1.0三種條件，對全離散色散耗散特性關于γdisp和γdiss的靈敏度進行測試，結果如圖4～圖6所示。

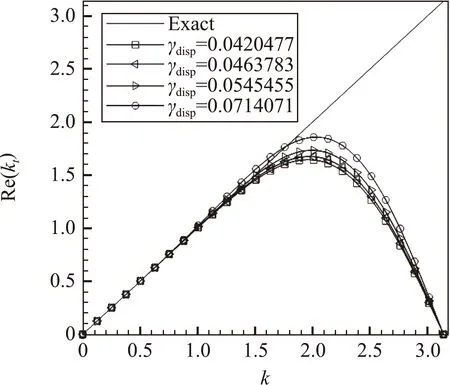
(a) 不同γdisp下的全離散色散特性

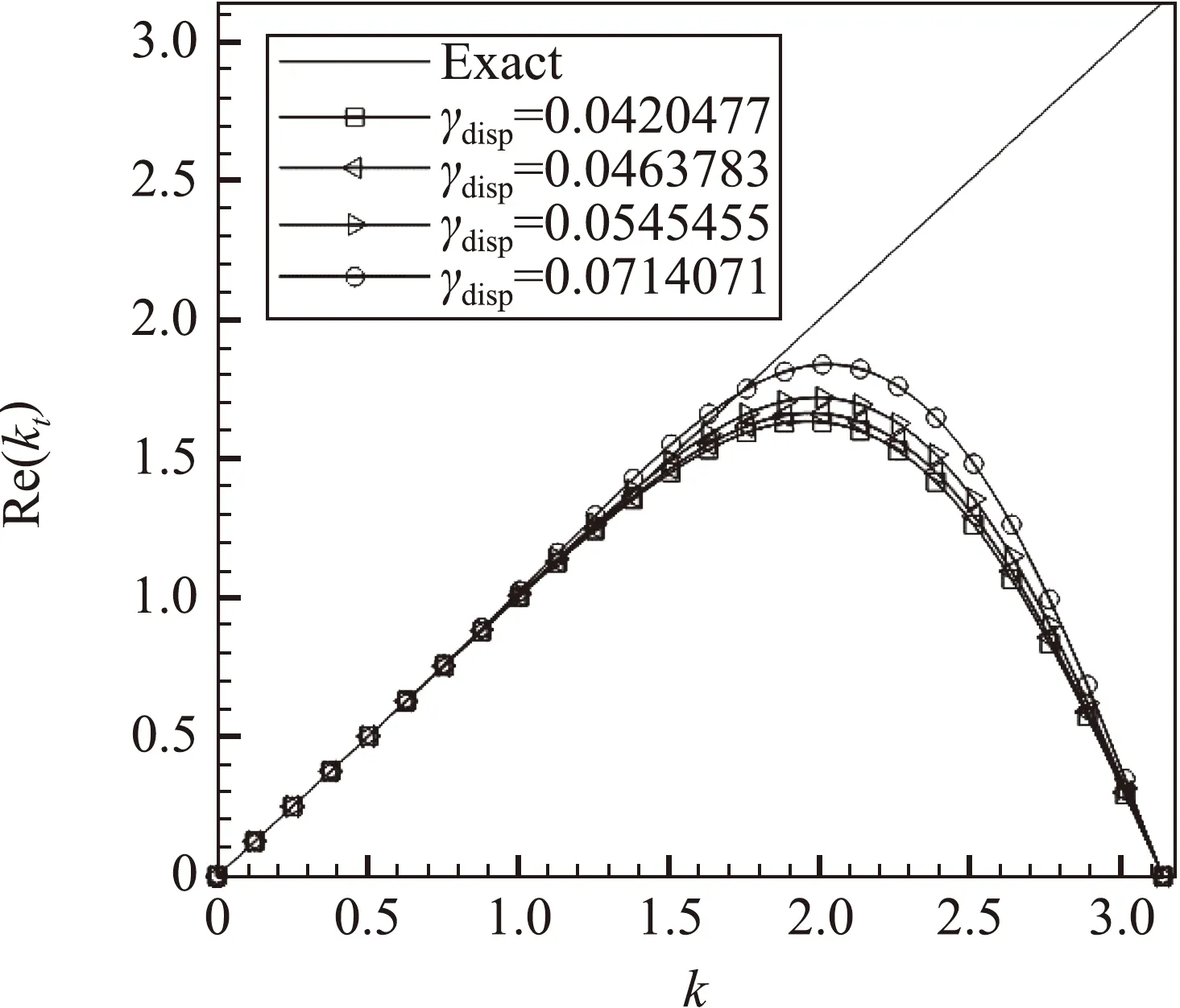
(a) 不同γdisp下的全離散色散特性

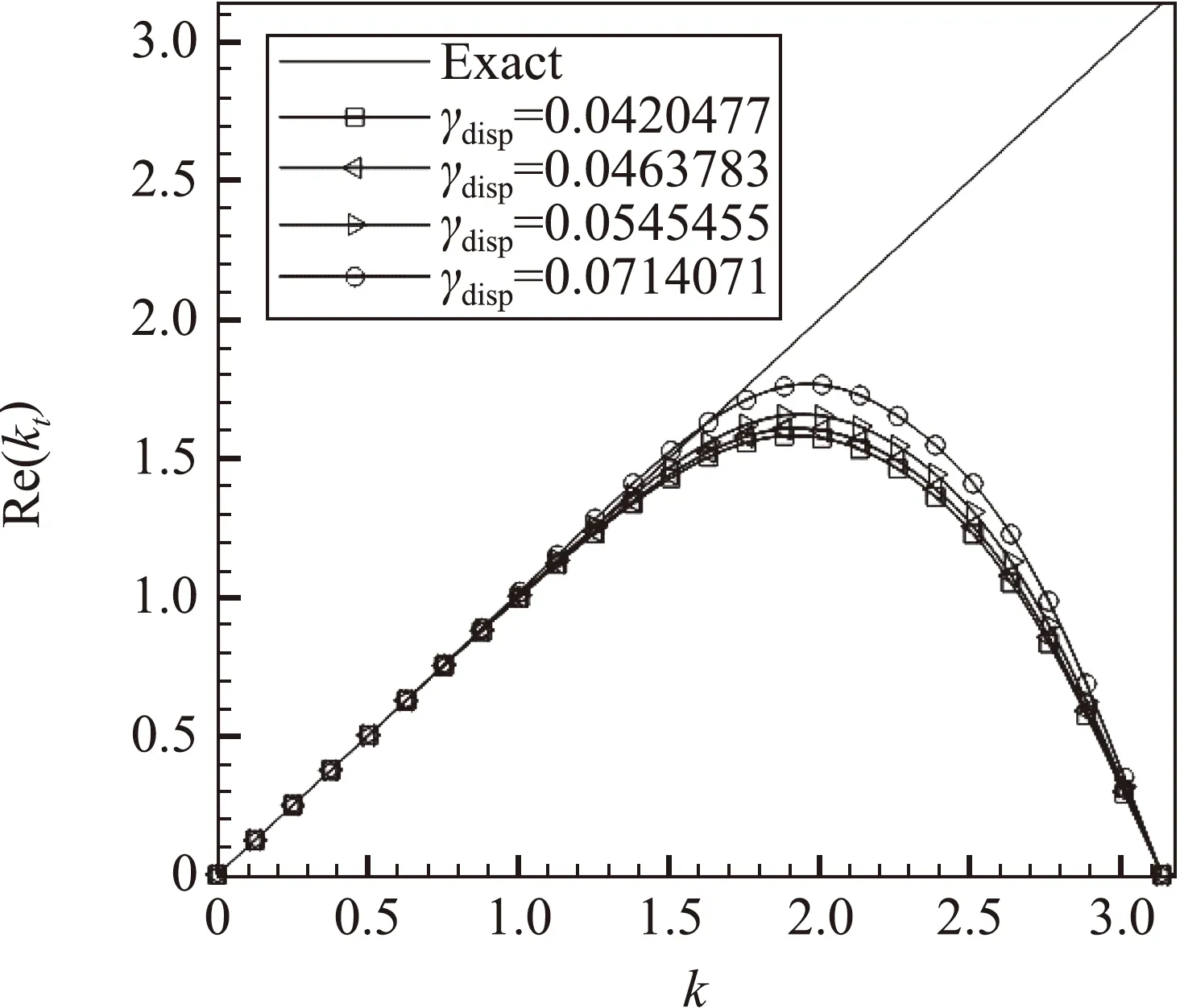
(a) 不同γdisp下的全離散色散特性

可以看到，當庫朗數較小(c=0.3、0.6)時，格式的全離散色散耗散特性受時間離散影響尚不明顯，主要由空間離散決定[24]，此時全離散色散特性主要受色散參數γdisp控制，對耗散參數γdiss不敏感，而全離散耗散特性主要受耗散參數γdiss影響，對色散參數γdisp不敏感。但當庫朗數c=1.0時，時間離散帶來的誤差與空間離散相當，此時全離散色散耗散特性表現出同時受色散參數γdisp和耗散參數γdiss影響。但是色散參數γdisp對耗散的影響仍比耗散參數γdiss小得多，而耗散參數γdiss對色散的影響也比色散參數γdisp小得多。因此可以認為，在全離散意義下，MDCD格式仍是可用的。

2 色散最小、耗散自適應有限差分格式

在1.1節中，我們采用Hu等[23]提出的色散耗散條件確定了一個通用的四階MDCD格式的耗散參數。但是我們也注意到，當流場尺度較大時，可以采用更小的數值耗散，因為此時物理耗散可被準確地預測以使計算穩定。在某些情況下，對于可精確分辨的解，采用中心格式計算已經足夠[9]。因此，當全場采用相同的耗散參數時，在流場尺度較大的光滑區，可能出現耗散過大的情況。

理想的耗散參數應該隨著解的局部尺度而自動調節。為了實現這一目標，必須發展數值解的尺度識別器，并在此基礎上構造具有最小色散、自適應耗散特性(Minimized Dispersion and Adaptive Dissipation, MDAD)的格式[25]。本節綜述這方面工作的最新進展。

2.1 數值解尺度識別器

原則上，在解的局部尺度遠大于網格尺度時，線性格式的耗散應該很小甚至為0，以提高格式的分辨率。而當解的局部尺度與網格尺度接近時，應該將耗散增加到足以抑制高波數振蕩的水平。如果能夠實現這一點，則MDCD格式在魯棒性不下降時，分辨率將得到進一步改善。為此，本節將提出一種數值解局部尺度識別器，用于識別數值解局部的等效長度尺度，作為構造自適應耗散格式的第一步。

數值解尺度的確定是一個開放性的問題，目前相關的研究很少。Li等[28]提出了一種尺度識別器，用于優化一種五點非線性格式，以計算擴散方程中的二階導數項。而文獻[25]提出了一種新的數值解局部波數識別器，用于自適應耗散格式的構造。

設計尺度識別器的難點在于定量描述尺度時看似矛盾的兩個要求。一方面，考慮到我們關注的是解的局部特性，尺度識別器應該作用于局部的物理空間。另一方面，為了將尺度識別器用于耗散控制，需要將其表示為波數的形式，而波數是傅里葉空間中的概念。為了滿足上述兩個條件，文獻[25]提出一種兩步的構造校準方法，即首先基于物理空間構造一種尺度識別器，之后再采用正弦波來校準尺度識別器中的參數。

第一步：構造。考慮光滑函數f(x)，為了估計其在x0附近的長度尺度，將其在x0處作Taylor展開，有：

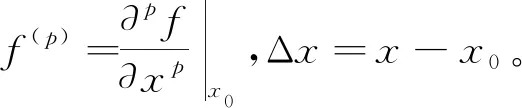
當數值解的尺度較大時，低階導數對函數變化的影響比高階導數大。例如，當解為直線分布時，只有Δf1對解的變化有貢獻。而x0附近如果出現小尺度結構，則說明高階導數項產生的影響足夠大。因此，原則上數值解的無量綱尺度可以用不同Δfp的比值來表示：

其中δ為局部無量綱尺度，且p>q。將式(26)代入式(27)得到：

其中β是待定參數。考慮到四階MDCD格式數值通量的模板點為6個，可以數值計算的導數f(p)的階數為p=1～5，這里選取p=1～4構造尺度識別器，但此時仍然有多種可能的p-q組合方式。為了解決這個問題，可以采用如下的校準步驟。

第二步：校準。在這一步中，采用正弦波來確定式(28)中的參數。若將式(28)定義的長度尺度校準為精確的正弦波無量綱波長，最簡單的方式是令p=q+2，此時p-q只剩如下兩種組合方式：

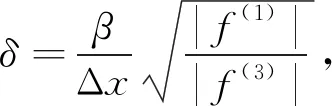
證明過程如下。考慮單一正弦波，

f=Asin(ωx+φ)

(30)

可以得到它的各階導數：

f(1)=Aωcos(ωx+φ)

f(2)=-Aω2sin(ωx+φ)

f(3)=-Aω3cos(ωx+φ)

f(4)=Aω4sin(ωx+φ)

(31)

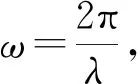
因此，當β=2π時，無量綱尺度δ即為精確的無量綱波長，

基于式(33)，定義解的等效無量綱波數k,

將式(29)代入式(34)，并令β=2π，則有：

需要注意的是，式(35)定義的等效無量綱波數并不是傅里葉空間中的波數，而是局部長度尺度的倒數，是一個物理空間中局部的定義。對于單一正弦波，它可以得到精確的正弦波無量綱波數。為了避免式(35)在極值點和拐點附近的奇異性，可以把該式的兩種情況相結合，從而有:

其中ε為防止分母為0的小量，取ε=1×10-3。

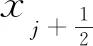
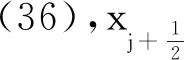
為了驗證尺度識別器在流場中的效果，Li等[25]采用如下四組指定的函數進行靜態測試，其中包括:

(a)f=sin(16πx) , -1≤x≤1

(d)f=sin(2πex+1x) , -1≤x≤1

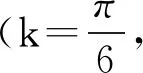
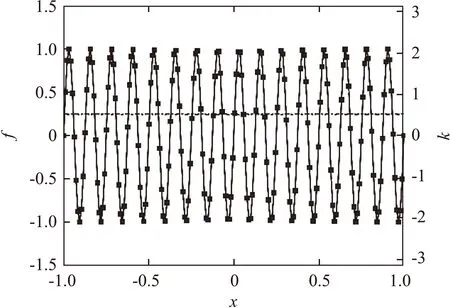
(a)

由測試結果可知，尺度識別器能夠準確地識別標準正弦波的無量綱波數，對于幅值增加和頻率增加的正弦波識別效果也很好。式(38)通過各階導數的恰當組合，有效抑制了等效無量綱波數在極值點和拐點處的振蕩。而對于間斷，尺度識別器往往將其識別為一個高頻成分，這也與物理事實相吻合。

2.2 MDAD格式

2.1節已經介紹了可以用于判斷流場局部等效無量綱波數的尺度識別器，為了構造耗散自適應的MDAD格式，需要根據等效無量綱波數對式(7)中的耗散參數γdiss進行動態的調整。此時，γdiss在全場不再是一個常數。為了更清楚地介紹MDAD格式的構造過程，可以將式(7)改寫為：

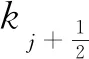
Li等[25]采用Hu等[23]提出的色散耗散條件指導式(40)的設計。需要注意的是色散耗散條件是在傅里葉空間中的關系，然而自適應耗散應該在物理空間中實施。因此，使用該條件時需要格外小心。不過對于單一正弦波，等效無量綱波數即為精確的正弦波波數，此時色散耗散條件可以很容易的使用。從這個角度考慮，使用色散耗散條件設計式(40)也可以看作是一個校準的過程，即以單一正弦波為例，采用色散耗散條件構造耗散參數與等效無量綱波數之間的關系，并應用于更一般的情況。需要注意的是，式(40)也可以基于經驗或者物理意義進行設計，這一問題將在接下來的工作中繼續研究。

1.1節中提到，當限制色散耗散比值r(π)≤9時，滿足條件的最小耗散參數為γdiss=0.012。考慮到MDCD格式的色散和耗散特性均為已知函數，則當r固定時，可以反推不同波數下所需的耗散參數。將式(14)代入式(16)可以得到耗散參數與波數的關系式：

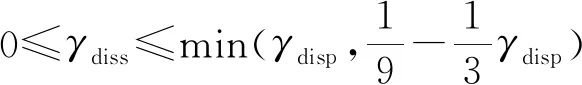
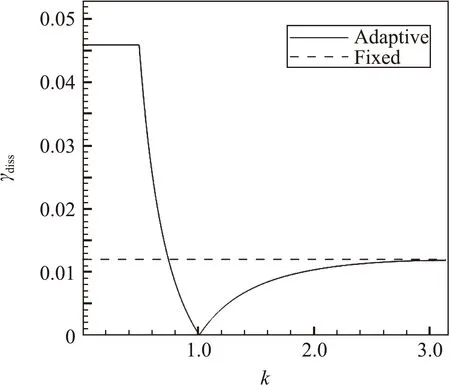
圖8 耗散參數與波數的關系(實線為自適應耗散參數，虛線為固定的耗散參數0.012)

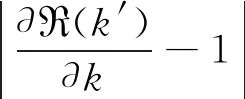
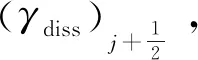
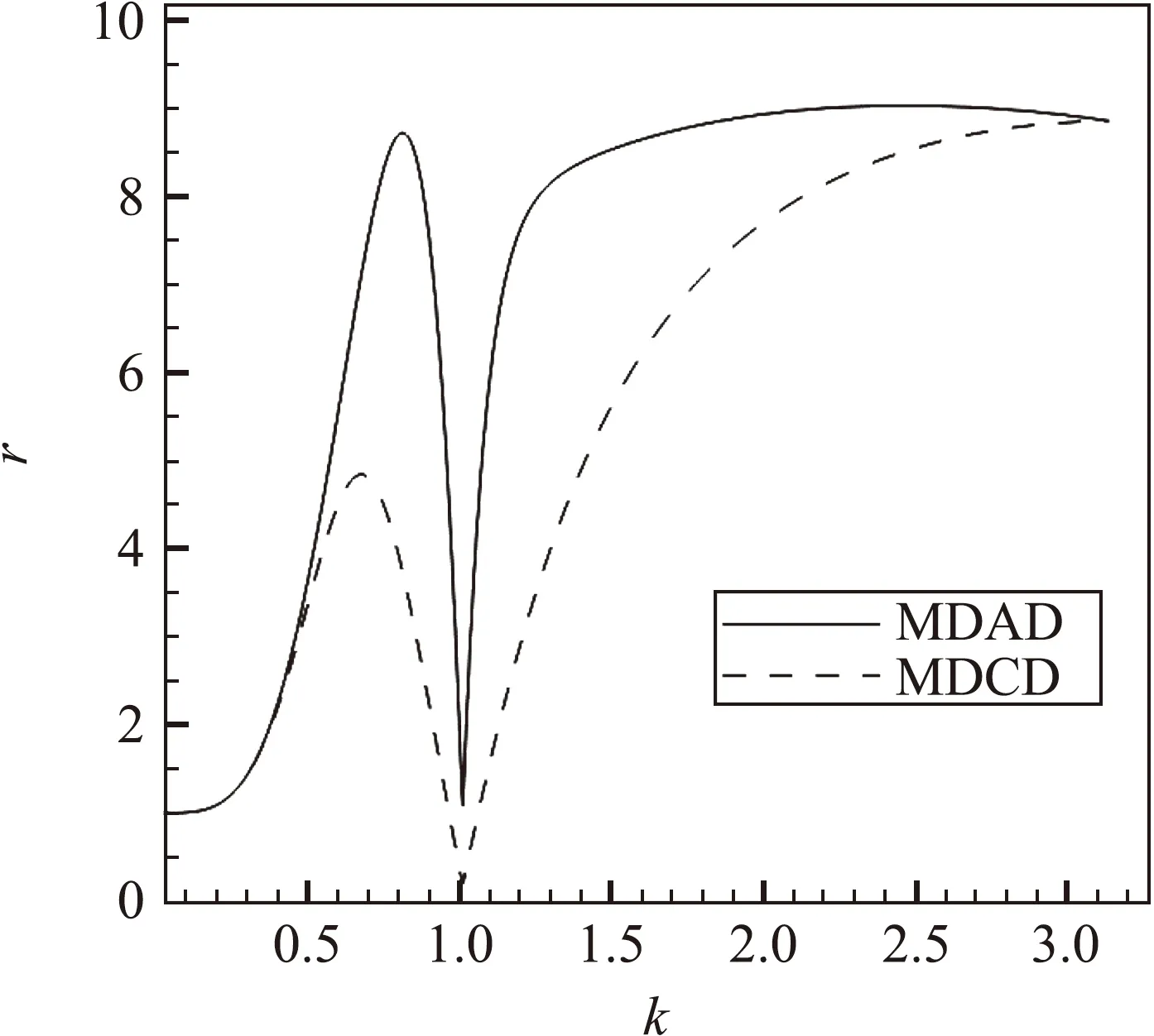
圖9 色散耗散比值r隨波數的變化曲線

3 混合格式

雖然MDCD格式和MDAD格式有很好的色散耗散特性，但它們不能直接用于含間斷流場的數值模擬。為了使這些格式具有激波捕捉的能力，Sun等[22,24]和Li等[25]的方案是首先將這些格式與WENO格式相結合，發展相應的非線性格式，之后將線性格式與非線性格式相結合，構造混合格式。由于MDCD格式與MDAD格式在混合格式構造方面基本一致，本文我們只介紹MDAD格式對應的混合格式MDAD-HY。本節將首先介紹MDAD-WENO格式，之后介紹一種新的間斷探測器用于MDAD-HY格式的構造，并用近似色散關系(ADR)[26]對混合格式的譜特性進行分析。需要注意的是，引入自適應耗散機制后，MDAD格式實際上是非線性的，但為了簡便，在后文我們仍然稱其為線性格式。

3.1 MDAD-WENO格式

WENO格式[2]是一類代表性的非線性激波捕捉格式，在含間斷流場的數值模擬中有廣泛的應用。WENO格式的基本思想是通過對一系列候選模板上低階多項式的非線性組合，實現無振蕩的激波捕捉能力。為了構造MDAD-WENO格式，可以采用包含對稱的6個模板點的MDAD格式作為它的線性部分，這些模板點被劃分如圖10所示的四條候選模板{S0,S1,S2,S3}，則MDAD格式的數值通量可以改寫為:

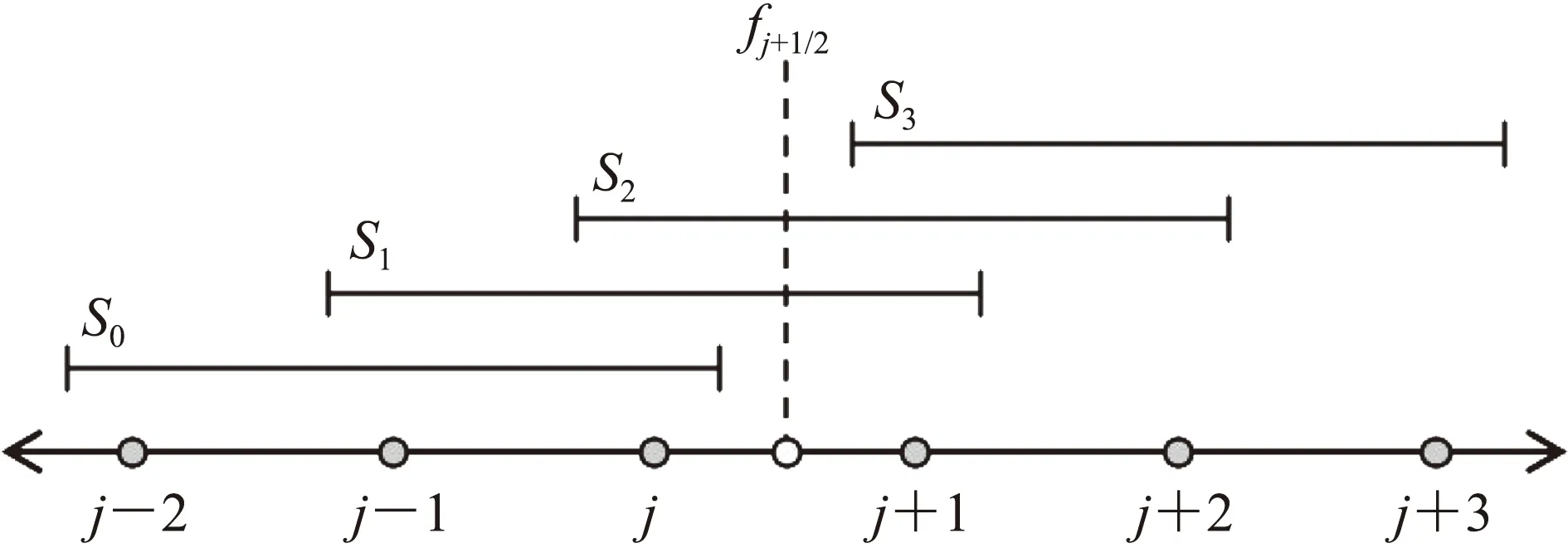
圖10 MDAD格式數值通量的候選模板Sk

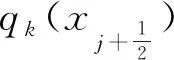
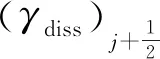
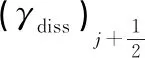
表1 線性權Ck關于γdisp和的表達式

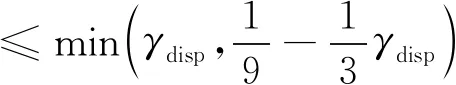
其中qk與式(43)意義相同，ωk為WENO格式的非線性權，與對應候選模板Sk上解的光滑性有關。MDAD-WENO的非線性權采用與Jiang和Shu[2]相同的形式:

其中Ck采用表1中的關系計算，因此MDAD-WENO格式也是耗散自適應的。ε為防止分母為0的小量，p與候選模板自適應的敏感性有關，通常取p=2，而βk為對應候選模板上解的光滑因子:

代入每個候選模板得到:

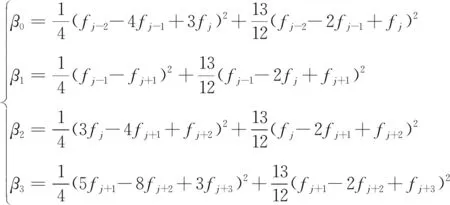
(48)

然而需要注意的是，與WENO-JS不同，MDAD-WENO是采用對稱的模板，正如文獻[8]中所說，它的候選模板S3包含的全部為順風模板點，當該模板的非線性權ω3大于其他非線性權時，有可能會引起格式的不穩定，因此，在式(48)計算完所有非線性權之后，需要對β3增加額外的限制,

以此來限制非線性權ω3不大于其他線性權，保證格式的穩定。

3.2 MDAD-HY格式

WENO格式能夠很好地捕捉流場中的間斷，但是相比對應的線性格式，由于引入了非線性機制，色散耗散特性往往會變差[26]。為了在提高格式分辨率的同時仍然保持良好的間斷捕捉能力，一種思路是采用合適的方法將WENO格式與譜特性良好的線性格式進行混合，在流場光滑區采用線性格式，在間斷附近采用WENO格式。文獻[25]對MDAD格式和MDAD-WENO格式進行組合，構造了具有耗散自適應、低色散特性的四階有限差分混合格式(MDAD-HY)。

MDAD-HY格式的數值通量可表示為：

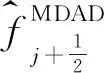
其中，

ε為防止分母為0的小量，

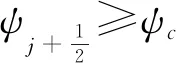
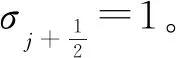
為了驗證新的間斷探測器的效果，我們將其與Harten[15]、Jameson等[16]以及Ren等[13]提出的基于一階導或者二階導的間斷探測器進行比較。Harten的間斷探測器同樣基于流場梯度的變化，具體形式如下:

(56)

其中,閾值ψc=0.3，ε為防止分母為0的小量。而Jameson提出的間斷探測器基于歸一化的二階導數:

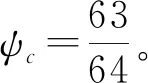
采用2.1節中的(b)算例對間斷探測器進行靜態測試，結果如圖11所示。可以看到，Harten和Jameson的間斷探測器能夠識別間斷，但是在正弦波光滑區都出現大量誤判，這將嚴重影響混合格式的分辨率。Ren提出的間斷探測器識別效果相對較好，但在光滑區部分極點附近也存在誤判。Li提出的新的間斷探測器不僅能夠準確識別間斷，而且由于引入了尺度識別器的結果進行截斷，光滑區的識別結果得到很大改善。

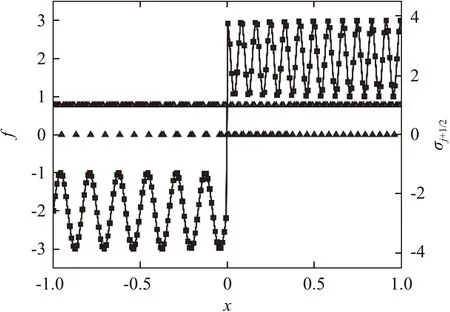
(a) Harten

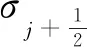
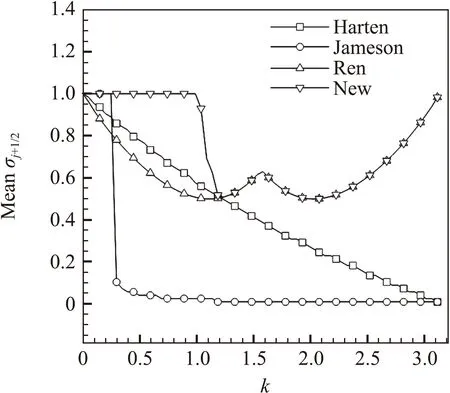
圖12 間斷探測器在不同波數下測試得到的的平均值

3.3 MDAD-HY格式的譜特性

線性格式的色散耗散特性可由傅里葉分析得到，但是對于非線性格式，目前還沒有解析的分析譜特性的方法。Pirozzoli[26]提出一種近似色散關系(Approximate Dispersion Relation, ADR)，可以數值地計算非線性的激波捕捉格式的修正波數，從而得到非線性格式近似的色散耗散特性。本節將利用ADR分析MDAD-HY格式的色散耗散特性，并與原始的MDCD-HY格式[22]進行對比。

圖13展示了不同格式的近似耗散特性，Jiang和Shu[2]提出的WENO格式(即圖中的WENO-JS)，Borgers[5]提出的WENO-Z格式，以及Sun等[22]提出的線性MDCD格式也被引入作為參考。可以看到，WENO-Z的耗散小于WENO-JS，但是仍比兩種混合格式要大。混合格式MDCD-HY和MDAD-HY的耗散特性在低波數和高波數段與線性MDCD格式接近，但在中波數段耗散變大。通過局部放大，可以觀察到MDAD-HY在k<1.04時耗散為0，小于MDCD-HY的耗散，之后隨著波數的增加，耗散逐漸增大，直到k>2.5后MDAD-HY的耗散特性曲線與MDCD-HY基本接近。這就說明MDAD-HY格式在低波數段相比MDCD-HY有更好的分辨率，而在高波數段能提供和MDCD-HY相似的耗散來抑制數值振蕩，具有較好的魯棒性。

(a)

圖14為不同格式的近似色散特性對比，可以看到MDAD-HY和MDCD-HY的色散特性非常接近，在高波數段稍差于MDCD，但遠好于WENO-JS和WENO-Z。

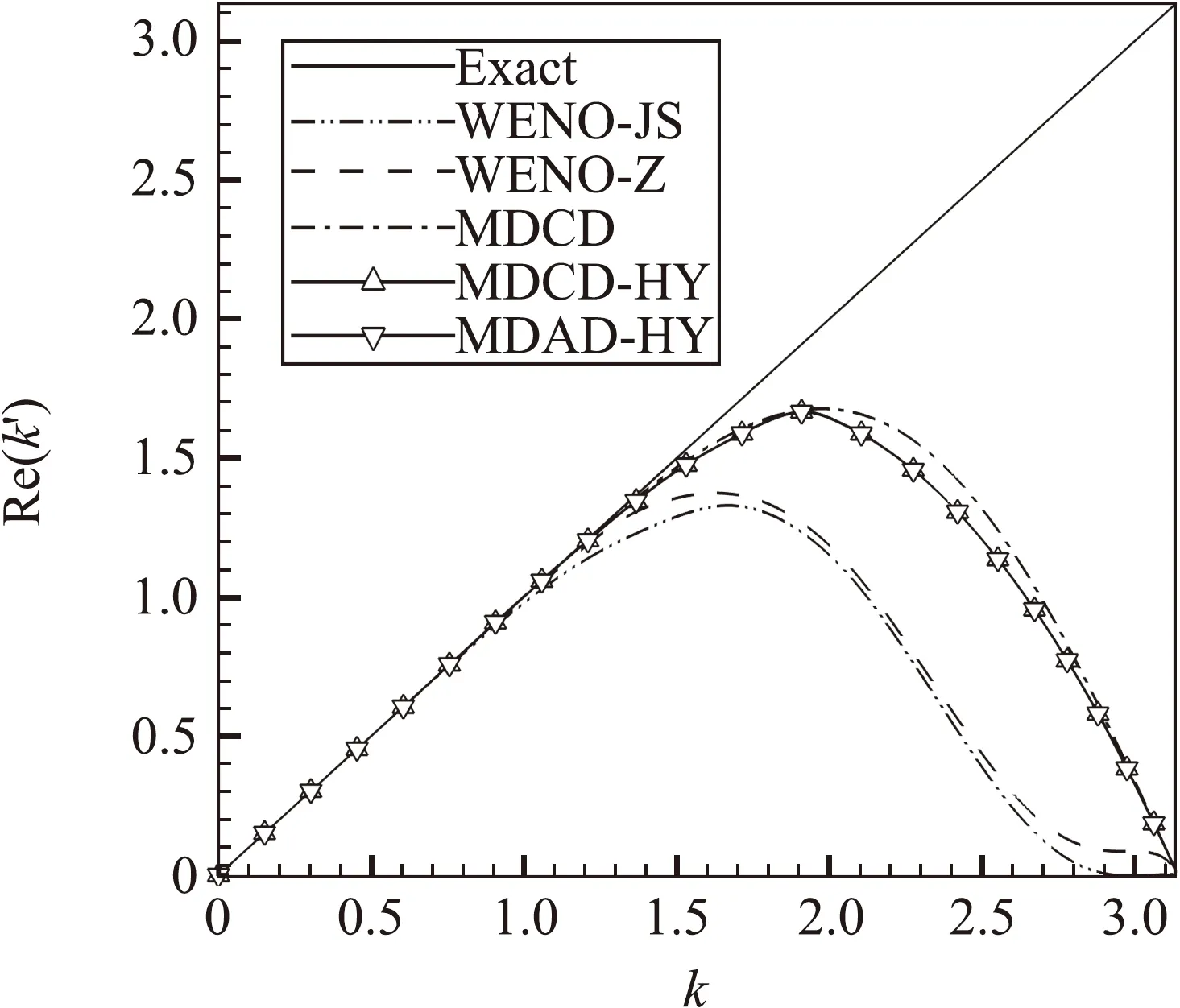
圖14 不同格式的近似色散特性

4 MDCD格式的發展應用與MDAD格式的算例測試

前面我們以線性波動方程為例介紹了MDCD和MDAD格式，這些算法很容易推廣到Euler方程和N-S方程。具體方案是：采用特征分解[29]的方法計算無黏數值通量，尺度識別器和間斷探測器都作用于特征分解后的局部特征通量。更多細節可以參考文獻[22,30]。而黏性通量采用文獻[31]中的方法進行計算。時間積分采用低存儲的四階龍格-庫塔格式[32]，也可以采用常見的隱式格式。

MDCD格式自提出以來，得到了持續的發展和廣泛的應用，而MDAD格式及其對應的混合格式MDCD-HY最近才被提出。因此在本節中，對于MDCD格式我們主要介紹其發展和應用，而對于MDAD格式，我們主要介紹其在求解一些標準算例中的表現。

4.1 MDCD格式的發展及應用

MDCD格式[22]自提出以來，得到了一定的發展和應用。原始MDCD格式是四階精度的，Sun等[24]研究了六階精度的MDCD格式，并初步研究了耗散控制問題。Wang等[33]將MDCD格式推廣到有限體積格式，通過采用多塊結構網格，使算法具備了模擬復雜幾何外形的能力。圖15是用有限體積MDCD格式得到的AIAA CFD HiLiftPW-1多段翼模型標準算例的壓力分布云圖。圖16是41%翼展的壓力系數分布，對比同樣網格上MUSCL格式的計算結果，可以看到MDCD格式預測的壓力分布更接近實驗結果。

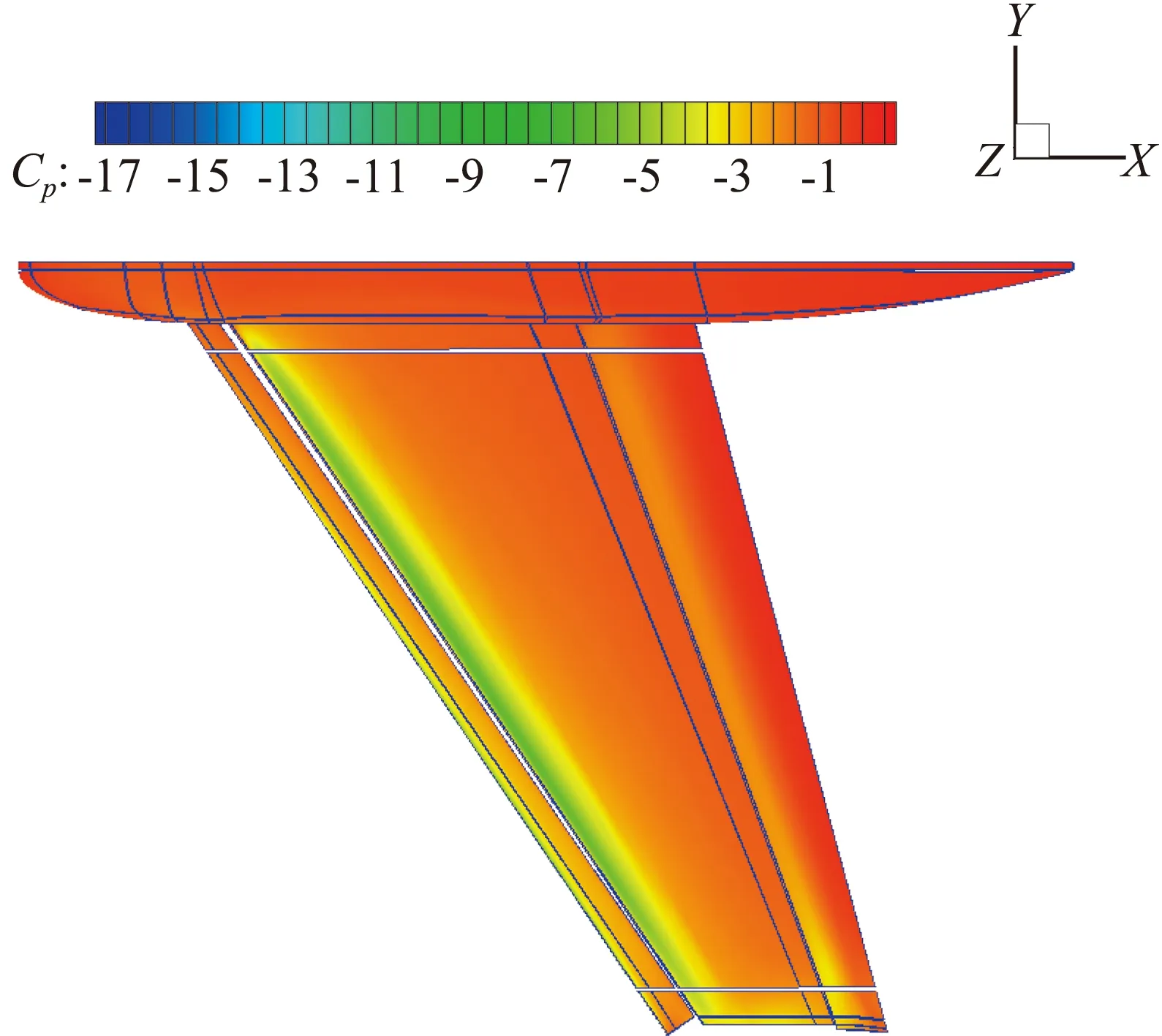
(a) 機身壓力分布云圖

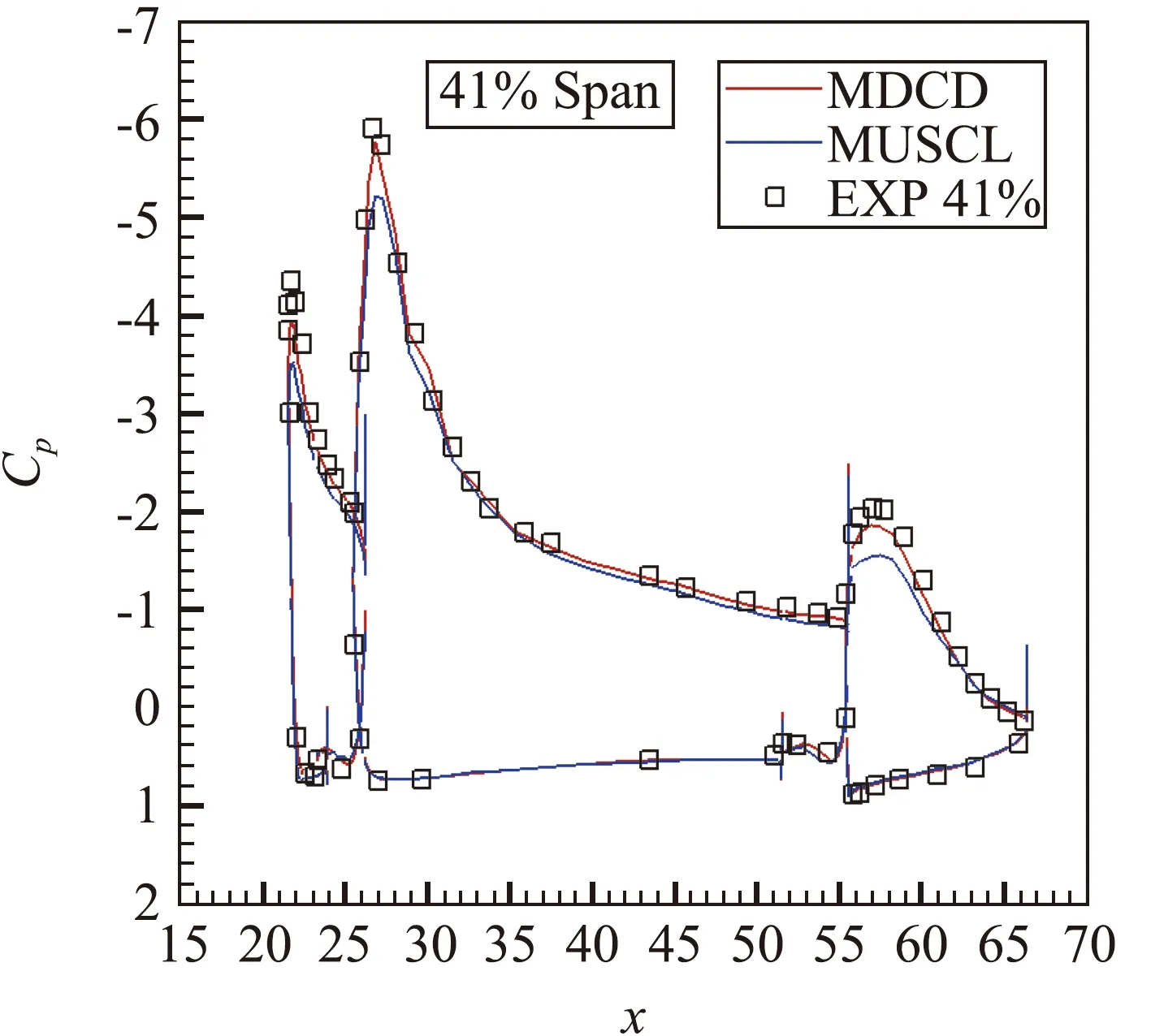
圖16 41%翼展壓力系數分布

文獻[34-35]將MDCD格式發展到求解多介質復雜流動，并研究了激波與多物質界面作用產生的界面不穩定性和湍流混合問題。圖17是激波與氦氣泡作用后，界面失穩的形態。

圖17 激波與氦氣泡作用后的界面不穩定性

此外，Li等[36]、Chen等[37]利用MDCD格式耗散可調的特點，研究了MDCD格式的耗散對隱式大渦模擬的影響。Jiang等[38]把MDCD格式與SIMPLE算法相結合，將MDCD格式推廣到求解不可壓縮流動，顯著提高了算法的分辨率。Duan等[39-40]把MDCD格式應用于高超聲速邊界層粗糙元誘發轉捩問題的直接數值模擬，Jiang等[41]把MDCD格式應用于低壓渦輪分離誘導轉捩的預測，Yang等[42]把MDCD格式應用于基于渦流發生器的流動控制研究。這些應用充分說明了MDCD格式解決實際科學與工程問題的能力。

4.2 MDAD格式算例測試

MDAD格式是MDCD格式的進一步發展，本節通過典型算例說明MDAD格式具有比采用傳統耗散控制方法的MDCD格式具有更好的性能。由于篇幅的限制，我們只介紹二維無黏和黏性流動兩個算例，更多的測試算例請參見文獻[25]。

4.2.1 雙馬赫反射問題

考慮文獻[43]中提到的雙馬赫反射問題作為二維驗證算例。該算例的控制方程為二維Euler方程。一個馬赫數為10、與x軸夾角為60°的激波向右移動，并與下壁面發生反射。初始條件如下:

其中x0=1/6，計算域為(x,y)∈[0,4]×[0,1]。邊界條件方面，在下邊界，為了使激波附著在壁面前緣，x∈[0,x0]段采用激波后的參數，而x∈[x0,4]段為滑移壁面。入口和出口分別采用來流和出流邊界條件。上邊界采用精確的波前波后參數，并隨著激波的移動而變化。

圖18展現了計算時間t=0.18時不同格式的密度等值線，網絡量采用800×200，庫朗數Nc=0.3。可以看到，WENO-JS、WENO-Z、MDCD-HY和MDAD-HY均能很好地捕捉到流場結構，包括馬赫桿和壁面射流。但是，MDAD-HY在第二個三波點附近的渦結構明顯更加細致，對小尺度結構捕捉更好。這說明相比于其他三種格式，MDAD-HY格式有著更高的分辨率。

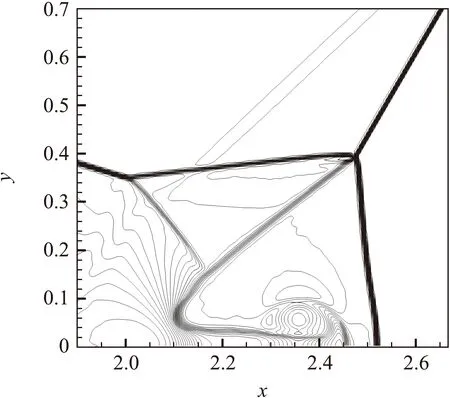
(a) WENO-JS

4.2.2 弱激波與等熵渦相互作用問題

為了研究不同格式在二維N-S方程中的效果，可以考察帶有黏性的弱激波與等熵渦的相互作用問題[44]。該算例的計算域為[0,2L0]×[0,2L0]，其中參考長度L0=1.0。一個靜止的平面激波位于x=1.0，波前來流參數為ρ0=1.0，p0=1/γ，預設的激波前后壓差為Δp/p0=0.4，對應的激波強度為M0=1.1588，其余的流場參數由Rankine-Hugoniot關系確定。雷諾數Re=5000，它的參考長度為L0，參考密度和參考速度均為來流參數。初始狀態下，一個孤立的等熵渦被疊加在來流中，渦中心位于(x0,y0)=(0.5,1.0)，它表現為速度(u,v)和溫度T=γp/ρ的擾動，而熵S=p/ργ為常數。

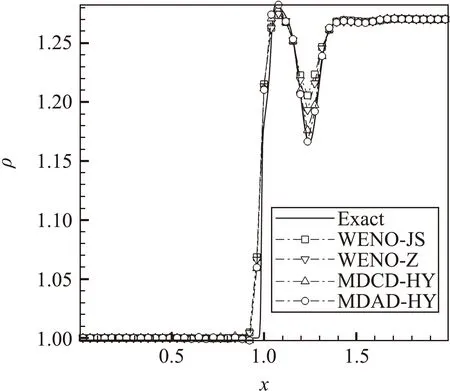
(a) t=0.7時中心線上的密度分布

5 結 論

本文綜述了我們在有限差分格式的色散優化和耗散控制等方面的工作。相應的計算格式可以計算無激波的光滑解，也可以作為非線性激波捕捉格式(如WENO格式)或者混合格式的線性部分。

在理論上，我們得到了半離散格式色散、耗散獨立的充分條件，使色散優化和耗散控制不相互干擾，為格式性能優化打下了基礎。進一步的分析表明，即使對于全離散格式，上述充分條件也可以保證色散和耗散近似獨立。

以此為基礎，我們得到了色散最小、耗散可控的MDCD格式，該格式的優良性能已經在一系列應用中得到了驗證，并被推廣到有限體積方法，以及求解多介質流動、不可壓流動等。MDCD格式的主要缺點在于耗散控制。無論是采用試錯方法還是基于色散、耗散條件確定通用耗散參數，得到的格式在耗散特性方面仍有很大的改進空間。

為了解決耗散控制問題，我們提出了將數值耗散與數值解的尺度相關聯的思路。為此，我們首先提出了一種基于數值通量模板點上導數的尺度識別器，用于判斷流場局部的等效無量綱波數。然后通過色散耗散條件[23]，設計出耗散參數與等效無量綱波數之間的關系，從而實現耗散參數的自適應調節，提出了色散最小、耗散自適應的MDAD格式。

我們通過所發展的格式與WENO格式相混合的方法，使MDCD和MDAD格式在能夠高精度、高分辨率的求解光滑流動的同時，具有魯棒的激波捕捉能力。我們發現，通過在混合格式的激波探測器中，引入基于尺度識別器的修正，可以進一步提高混合格式的性能。

由于MDCD格式的性能已經得到了充分的驗證，且MDAD格式在多個標準算例中都表現出優于MDCD格式的性能，可以預見，MDAD格式及其對應的混合格式MDAD-HY在求解含激波的復雜多尺度流動中也有很好的應用前景。

致謝:李萬愛、潘建華、曾衛剛、黃文鋒、李星輝、張宏杰、李俊濤、張潤東等參與了計算程序開發、驗證、應用等工作，特致感謝。