非結構網格緊致高精度氣體動理學格式

李啟兵, 張 潮

(清華大學 航天航空學院, 北京 100084)

0 引 言

計算效率是CFD格式在復雜流動模擬中面臨的核心問題。非結構網格能更好地適應復雜外形，網格生成和自適應動態調整自動化程度高，能極大地減少網格生成工作量。發展非結構網格上的高效數值格式，具有重要的理論研究和工程應用價值，也具有很大的挑戰性。緊致高階精度重構和高效通量演化方法是其中的關鍵。此外，還需要考慮格式的并行效率以及穩健性等因素。

傳統有限體積法由于每個單元只包含單元平均值，難以實現緊致高階重構。這里的緊致是指重構模板最多只包含面相鄰單元。緊致的計算模板不僅能更好地與可壓縮流動的局域性相容，而且能有效避免非緊致帶來的一些弊端。例如，由于非結構網格分布的任意性，距離較遠的模板單元的選取較為復雜。此外，模板單元過多也會導致緩存利用率和并行效率降低、計算域邊界處理更加困難，而且網格質量對重構的影響較大。

內自由度方法通過在網格單元內設置足夠的自由度來實現緊致重構，并利用控制方程對每個內自由度加以記錄和更新。這里的自由度表示的是每個單元內記錄的離散信息，如內點值、子單元平均值或多項式展開系數，與氣體動理論中涉及的氣體分子的自由度是不同的概念。內自由度方法中最具有代表性的是間斷伽遼金(DG)方法[1-2]，也是目前最為流行的非結構網格高精度方法。Huynh 針對一維雙曲守恒律提出了一種簡單高效的內自由度方法，稱為通量重構(Flux Reconstruction, FR)格式[3-4]。FR首先計算求解點(內點)上的通量值，并插值得到單元內的通量分布，再結合單元界面通量對其進行修正，從而可以直接計算通量散度值來更新守恒量。相比于傳統的DG方法，FR方法具有很高的效率。LCP 方法則通過引入提升算子的方式進行通量修正，從而使之適用于三角形和四面體網格[5]。FR和LCP后來統稱CPR方法，為多種內自由度方法提供了一個統一框架[6-7]。

相比于傳統有限體積法，內自由度方法不僅易于實現緊致重構，而且由于單元內多個自由度共享同一個連續的多項式分布，重構效率更高。同時，單元內的連續分布使得計算通量時不必求解Riemann問題，從而更為簡單高效。但是，在捕捉流場間斷時，單元內的連續分布難以描述間斷結構，重構時需要針對單元整體進行限制，從而導致分辨率的降低，相當于損失了自由度。在這方面，譜體積方法(SV)具有獨特的優勢[8-9]。它結合了內自由度方法和有限體積法的特點，在每個單元內劃分若干個子單元，將子單元平均值作為內自由度，按照有限體積法更新，保證了高階重構的緊致性。由于可以分別對每個子單元進行限制，因而能夠避免內自由度損失，實現在子單元尺度上捕捉間斷[10]。已有研究對DG和SV進行了混合[11-12]。但SV 格式對于子單元劃分的要求十分苛刻，對格式穩定性影響較大，不易推廣到四邊形或六面體網格。

利用面相鄰子單元參與重構，Pan 等發展了針對一維及二維四邊形網格上的雙曲守恒方程的子單元有限體積法(Subcell Finite Volume, SCFV)。相比于SV，SCFV劃分的子單元更少，也更簡單靈活[13-14]。這種通過引入面相鄰單元自由度參與重構的方法，集合了內自由度方法和有限體積方法的優勢，與DG結合后也能有效降低計算量，增大時間步長[15-16]。為獲得穩定的數值格式，重構時子單元的守恒性非常重要。SCFV通過一種簡單的平移修正來間接保證守恒性。但是，這會在單元內部的子單元界面上額外引入間斷，從而導致子單元界面的通量計算效率低于SV 方法。

除了高精度重構外，通量求解器也對CFD方法的精度和效率起著重要的影響作用。傳統CFD方法多是基于宏觀Euler方程的Riemann解來計算數值通量。由于傳統的Riemann解只有一階時間精度，通常需要結合多步Runge-Kutta(R-K)方法進行時間推進。多步法中每個子步都需要進行重構、通量計算以及并行通信，影響格式的計算效率。Li和Du利用通量及其一階時間導數，提出了兩步四階方法，通過兩個子步達到四階時間精度[17]。基于廣義Riemann問題(GRP)通量求解器，兩步四階方法成功用于Euler方程的高效求解[18-19]。此外，傳統高精度格式需要分別計算無黏和黏性通量。由于計算黏性通量需要用到單元界面上的物理量的一階導數，而重構得到的兩側導數值通常是不連續的，從而使得計算往往較為復雜。

徐昆等提出的氣體動理學格式(GKS)為發展高精度格式提供了一條新的途徑[20-21]。GKS利用介觀BGK方程的局部解析解來計算網格界面上的數值通量。該局部解在連續流區可以用平衡態分布及其時空導數，即宏觀量及其時空導數來表示，因而GKS可以直接記錄和更新宏觀守恒量，避免了在微觀速度空間離散導致的巨大計算資源開銷。與N-S方程不同，BGK方程能描述任意重構初始間斷的演化，因而GKS能夠引入更為合理的數值耗散，具有很強的穩健性，同時也能更好地考慮多維特性[22]。由于缺乏多維Riemann解，這在傳統格式中是難以做到的。此外，GKS通量自動耦合了無黏和黏性影響，且包含時間的演化，只需要單步即可達到二階時間精度[23]。二階GKS在高馬赫數流動、多介質流動以及湍流等多種流動中顯示了優異的性能[24-27]。

為進一步提高計算效率，可以基于時空二階Taylor展開，利用BGK方程的局部解析解，建立時空三階精度的動理學格式(HGKS)[28-29]。由于通量中包含了三階時空演化，具有真正的多維特性，HGKS可以通過直接積分來計算界面通量，避免了采用數值積分時多個積分點上的通量計算[30-31]。同時，時間方向只需要單步推進即可達到三階精度，避免了傳統格式中采用多步法帶來的不足[32-33]。

將高階GKS拓展到非結構網格上時，同樣面臨緊致重構的問題。考慮到GKS構造了BGK方程的局部時空演化解來計算數值通量，該演化解可以用來直接計算界面上的宏觀量，從而為重構提供額外的信息，提高緊致性[34-36]。按照這一思路，已建立了三角形網格上的緊致三階HWENO-GKS[37-38]。如何更好地利用GKS提供的額外信息，進一步提高格式精度以及穩定性，是一個很有意思的研究方向。結合緊致最小二乘重構，也可以發展非結構網格上的高階GKS[39]，不過需要求解大型代數方程組，在顯式格式中計算量相對較大。Ren等基于DG框架發展了非結構網格上的高階GKS[40]，能夠有效保證緊致性。基于更加高效的內自由度方法，如CPR，有望發展更為高效的高階GKS。

在時間推進格式方面，由于GKS通量包含時間演化，可以直接積分得到每個時間步內的數值通量，從而建立單步高精度格式[29]。也可以借鑒兩步四階方法，利用相對更為簡單二階GKS通量及其一階時間導數，通過兩個子步獲得四階時間精度[41]。考慮到重構過程通常需要較大的計算量，更少的子步意味著更小的計算量，以及更高的并行效率。同時，GKS無需額外計算黏性通量，且內涵自適應耗散機制，將其與高效緊致重構方法相結合，充分挖掘其多維及時空演化特性，有望構造出高精度、高效率和強穩健性的數值格式。

本文旨在探討GKS通量求解器與高效緊致重構方法的有機結合，發展非結構網格上的高效高精度格式。首先將簡要介紹課題組近年來發展的幾種基于內自由度緊致重構的高精度動理學格式。將三階GKS通量求解器與SCFV和CPR相結合，構造了兩種單步時空三階格式SCFV-GKS和CPR-GKS。進一步將二階GKS通量與CPR結合，利用兩步四階方法構造了時空四階格式CPR-GKS，并結合SCFV及曲邊網格技術增強對流場間斷和復雜外形的模擬能力。在此基礎上，通過多種典型流動對這幾種格式進行驗證，對比分析不同格式的精度、效率以及激波捕捉性能。研究表明，結合高效的重構方法和時空演化的GKS通量，充分利用各自優勢，能夠建立更加高效、穩健的新型數值方法。

1 基于內自由度的緊致高精度GKS

1.1 GKS的基本原理

GKS基于介觀氣體動理論中的Boltzmann-BGK方程，

g=ρ(2πRT)-(K+3)/2e-[(u-U)2+ξ2]/(2RT)

(1)

其中，f=f(x,u,ξ,t)為氣體分子速度分布函數，u為分子平動速度，ξ為內自由度，內自由度數為K。g為平衡態分布函數，(ρ,U,T)分別為氣體的密度、速度和溫度，τ為分子平均碰撞時間，R為氣體常數。對BGK方程取矩，可以得到宏觀守恒量Q及守恒方程：

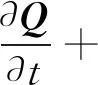
Fα=〈uαf〉,α=1,2,3

Ψ=(1,u,(u2+ξ2)/2)T

(2)

在連續流區，通過一階Chapmann-Enskog展開，

將分布函數近似用平衡態及其時空導數表示，可以導出宏觀的N-S方程。由此可以建立逼近N-S方程的動理學格式，且只需要記錄和更新宏觀量(對應平衡態分布)，避免在速度空間和內自由度空間的離散，使得計算量和傳統直接基于宏觀方程的CFD方法相當。

由方程(2)可以建立有限體積形式的GKS，

其中，Si為離散物理空間上網格單元i的界面面積，Ωi為單元體積。為計算網格單元界面數值通量，GKS利用BGK方程(1)的形式解：

e-t/τf0(x-ut,u,ξ)，

x′=x-u(t-t′)

(5)

來描述界面上任意重構初值的演化，其中，x′=x-u(t-t′)。該演化解描述了從初始分布函數f0向平衡態分布的時空演化，自動耦合了分子的自由運動和相互碰撞，這是確保基于該演化解的GKS成為真正多尺度方法的關鍵[23]。從宏觀上看，不僅耦合處理了無黏與黏性項，而且引入了隨時間變化的自適應數值耗散，保證了其在可壓縮黏性流動模擬中的優異性能。

在求解連續流區流動時，GKS基于式(3)，結合時空Taylor展開來構造初始分布函數f0，并且相應地用Taylor展開構造平衡態分布g，從而可以借助式(5)獲得界面上的演化解，進而直接計算數值通量。其中Taylor展開的階數對應于重構多項式階數，直接取決于格式精度的要求。通過二階Taylor展開，可以得到單元界面上具有時間和空間三階截斷誤差的分布函數(以二維為例，界面坐標x=0):

f(0,y,t,u,ξ)=flH(u)+fr[1-H(u)]+fc,

fc={C4+C5akuk+C6A+C8(A2+B)/2+

C7(akam+dkm)ukum/2+C9(Aak+bk)uk+

[C4a2+C6(Aa2+b2)+C5(aka2+dk2)uk]y+

C4(a2)2+d22)y2/2}g0

(6)

其中H為Heaviside 函數；上標s=l,r；下標k=1,2；m=1,2，系數:

C1=τ+t,C2=τt+t2/2,C3=τt,

C4=1-e-t/τ,C5=-τ+(τ+t)e-t/τ,

C6=t-τ+τe-t/τ,C7=-(t2+2τt)e-t/τ,

C8=t2-2τt,C9=-τt(1+e-t/τ)

(7)

分布函數中的各項展開系數可以由重構出的宏觀物理量各階導數及相容條件給出：

〈ak〉=?Q/?xk,

〈akam+dkm〉=?2Q/?xk?xm,

〈akum+A〉=0,

〈(akam+dkm)uk+Aak+bk〉=0,

〈(Aak+bk)uk+A2+B〉=0

(8)

單元界面上的守恒量及其一、二階導數可由高階重構得到。對氣體分布函數求矩即可得到二階時空分布的守恒量通量F(0,y,t)。由于其中包含了高階時空導數，只需要直接對時間和界面切向坐標積分就可以得到界面數值通量，從而建立單步時空三階精度GKS，且不需要布置高斯積分點，計算量得到顯著減少。

需要說明的是，式(6)中包含了界面兩側的初始間斷分布，從而有利于捕捉流場間斷。實際上，對于光滑區流動，比如CPR內點，式(6)可以簡化為：

f(x,t,u,ξ)={1-τakuk+(t-τ)A-

τt(Aak+bk)uk+(t2/2-τt)(A2+B)+

[ak-τ(akam+dkm)um+

(t-τ)(Aak+bk)]xk+

(akam+dkm)xkxm/2}g0

(9)

因此可以獲得整個單元內通量的時空分布F(x,t)，從而一次計算出所有內部點上的通量，減少計算量。

如果略去分布函數中的高階展開項，對應于二階GKS，式(6)可簡化為：

fc=(C4+C5akuk+C6A+C4a2y)g0

(10)

如果直接對時間積分，可以達到單步二階時間精度。實際上，由于該分布函數包含了一階時間導數項，可以結合兩步四階離散方法，從而高效地達到四階時間精度。通過結合新型的緊致重構框架，可以充分發揮三階GKS和二階GKS的優勢，構造出更加高效的高精度格式。

1.2 SCFV-GKS

SCFV方法具有混合方法的思想，其放寬了子單元數的限制，同時將重構模板拓展到面相鄰單元。這樣能夠有效避免SV方法劃分子單元的瓶頸。如圖1所示，為了滿足三階和四階緊致重構的需求，可以將每個單元(也稱為主單元)均勻劃分為4個子單元。子單元界面分為兩種類型，當界面(實線)兩側為不同主單元時，將其稱為I-型界面，而對于主單元內部的界面(虛線)則稱為II-型界面。

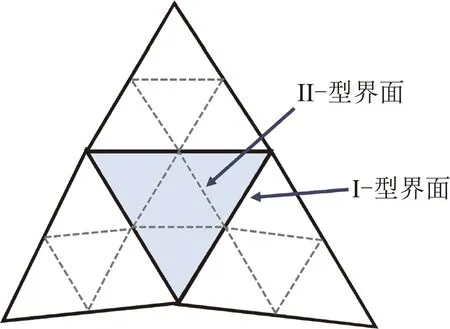
圖1 三階SCFV方法的子單元劃分

原始的SCFV方法采用加權最小二乘法重構單元內的分布，由此得到的多項式只能保證主單元的守恒性，其內部子單元的守恒性無法直接保證。Pan等采用了平移修正的方式對子單元守恒性進行修正，但這樣會在子單元界面上額外引入間斷，導致通量計算量的增大。

我們首先通過約束最小二乘重構對SCFV方法進行改進。在重構目標單元的多項式時，將目標單元的子單元平均值作為約束條件，并通過標準的拉格朗日乘子方法求解待定系數矩陣[42]。由此得到的多項式能夠直接保證子單元的守恒性，而無需進行額外的修正。在此基礎上，將緊致三階SCFV與三階GKS相結合，發展的了具有單步時空三階精度的SCFV-GKS。緊致三階重構模板僅包含目標主單元的4個子單元以及面相鄰主單元內的9個子單元。子單元平均值按照式(4)分別更新。

為計算子單元界面上的數值通量，可以基于式(6)，直接沿子單元界面切向和時間方向積分，從而不需要空間高斯積分點以及時間方向的R-K推進。值得注意的是，基于對SCFV方法的改進，僅I-型界面上保留了間斷。而II-型界面上的分布則是連續的，因此可以基于簡化的氣體分布函數式(9)進行計算，從而有效降低通量的計算量。同時，在光滑區域，由于重構是針對大單元進行的，不需要對每個子單元分別進行重構，同樣可以減小計算量。總之，SCFV-GKS不僅能保證緊致性，計算效率也能得到顯著提高。

為了實現激波捕捉，可以通過激波探測器標記問題單元，并在問題單元上實施基于逐級重構的WENO限制器[43]，該限制器能夠在保證光滑區域高精度的同時，有效抑制激波附近的數值振蕩。由于限制后的多項式無法直接保證子單元的守恒性，為簡單起見，仍采用原始SCFV方法中的平移修正來間接保證子單元的守恒性，實現子單元尺度上的間斷捕捉。SCFV-GKS的具體細節見文獻[44]。

1.3 基于CPR框架的高精度GKS

CPR框架的表達式如下：

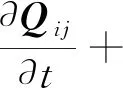
(11)

其利用單元內設置的若干求解點可以插值得到守恒量和通量在單元內的分布，從而可以直接對通量函數多項式求散度，進而更新每個求解點上的守恒變量Qij。考慮到單元界面兩側可能存在間斷，還需在每個單元界面上設置若干通量點，計算耦合相鄰單元影響的通量值，并由此對單元內的通量分布進行修正，即式(11)中的修正項δij。三階CPR的求解點和通量點分布如圖2所示，為減少計算量，求解點與通量點均采用Lobatto點，兩者位置重合。

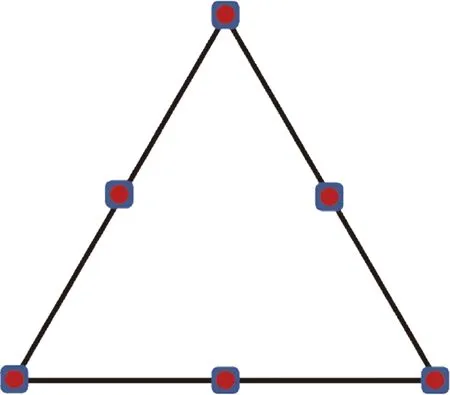
圖2 三階CPR的求解點(圓形)和通量點分布(方形)

我們首先基于CPR的緊致三階重構，結合三階GKS通量求解器，發展了單步時空三階精度的CPR-GKS。充分利用三階GKS的多維特性，基于單元界面中點，以及單元形心分別構造了時空二階分布的氣體分布函數，即式(6)和式(9)，進而得到通量在單元界面以及單元內的時空二階分布。由此可以同時確定單元界面上所有通量點，以及單元內所有求解點上的通量值。傳統CPR則需要逐點計算數值通量。同時，由于通量包含了時間演化，因此可以沿時間積分單步更新求解點值，而不需要結合多步R-K方法。此外，由于GKS中自動耦合了無黏和黏性影響，毋須像傳統CPR那樣額外處理黏性通量。格式的具體細節見文獻[45]。

為進一步提高格式精度，我們基于CPR的緊致四階重構，結合二階GKS通量及其時間導數，借助兩步四階離散，發展了兩步四階GKS，只需要兩個子步即可達到時空四階精度。而傳統CPR則通常需要結合四步或五步R-K方法。相比于單步四階GKS，采用兩步四階GKS能夠有效簡化氣體分布函數的構造，降低通量的計算量。

兩步四階CPR-GKS的高效性，來源于對GKS通量中包含的豐富時空信息的充分利用。類似地，單步三階CPR-GKS利用了GKS通量的多維時空特性，從而顯著提高了計算效率。Xu等利用界面上的演化解直接計算下一時刻的宏觀量，從而提高重構緊致性[34-38]。實際上，如果充分利用四階GKS通量的時空信息，也有望建立更為高效的數值格式。

雖然基于CPR框架能夠高效地實現緊致高階重構，但在高速流動問題中的激波捕捉技術尚待進一步研究。通過借鑒SCFV方法在激波捕捉上的優勢，我們進一步發展了CPR/SCFV混合算法。通過激波探測器區分流場中的光滑區域和包含間斷的區域，前者采用CPR求解，而后者則采用SCFV求解。這樣既能夠保證光滑區域的高精度，同時兼顧激波捕捉的高分辨率和強穩健性。傳統CPR限制器通常直接針對單元內的高階多項式進行限制，難以在亞網格尺度上捕捉間斷。而在CPR/SCFV混合算法中，通過將激波探測器標記的問題單元劃分為一組子單元，并且針對每個子單元分別進行限制。如圖3所示，對于三階CPR，將問題單元均勻劃分為9個子單元，這樣能夠在保證原有內自由度的同時，避免子單元劃分的復雜性。類似的，四階CPR則將問題單元均勻劃分為16個子單元。具體細節見文獻[46]。

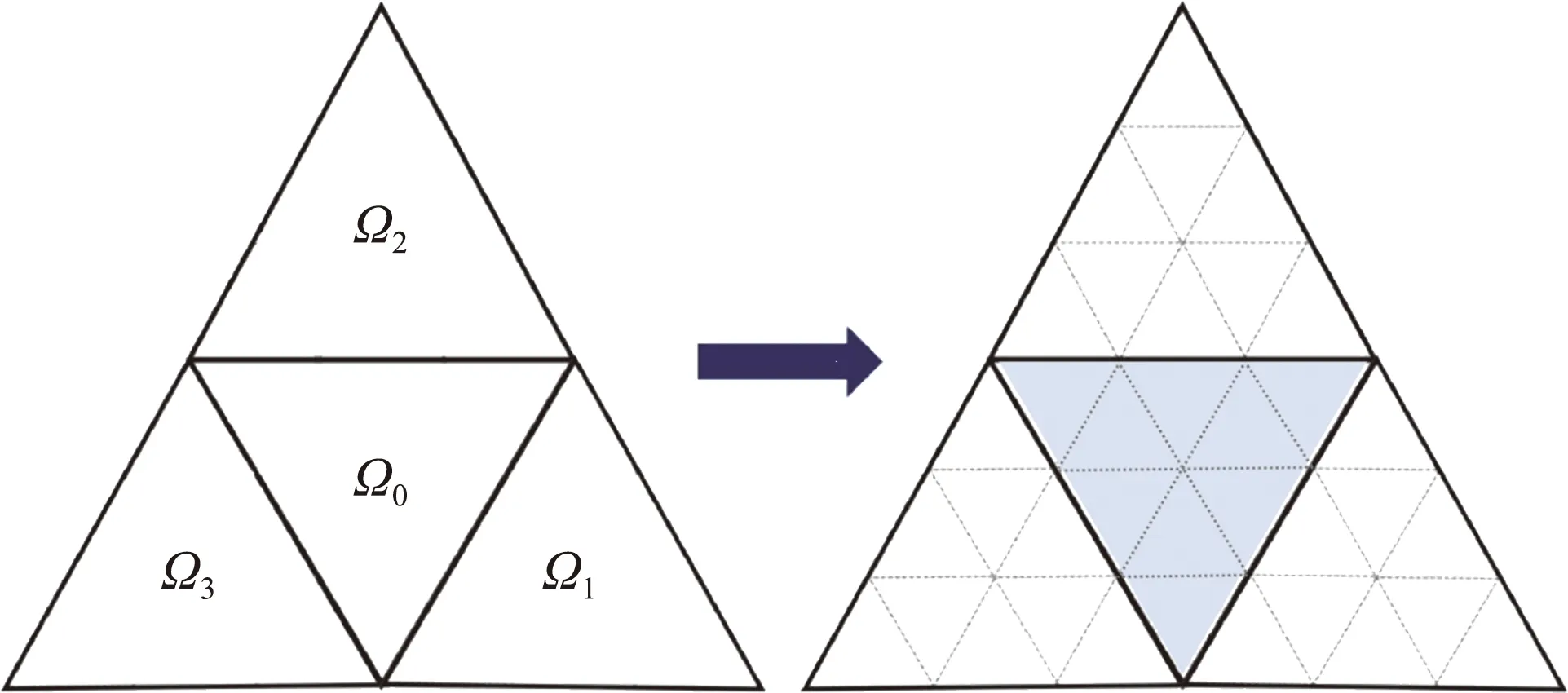
圖3 三階CPR的子單元劃分

通過在子單元界面上引入間斷，激波的厚度能夠被有效地限制在大單元尺度范圍內，從而實現子單元尺度上的激波捕捉。需要指出的是，我們在每個子單元上采用的是二階TVD限制器[10]，該限制器能夠較好地抑制數值振蕩，并且實現較為簡單，但引入的數值耗散較大，也在一定程度上增加了對激波探測器的依賴性。在后續的研究中，可以考慮針對子單元實施高階限制器。

高階格式在處理曲面邊界時，網格對物理邊界的逼近程度會嚴重影響數值計算精度，有必要采用曲邊網格。基于CPR 框架發展的高精度GKS，能夠比較方便地處理曲邊網格。只需通過等參變換將物理空間的高階網格單元變換到計算空間的標準單元上，并在標準單元實施CPR 算法即可。同時，由一維CPR 方法通過張量積的形式將其推廣到六面體網格，從而建立適合復雜外形的三維CPR-GKS。

2 數值驗證及對比分析

通過典型算例對前面提到的幾種格式進行驗證，考察不同格式的精度、效率以及激波捕捉性能。為了說明與傳統通量求解器的區別，還與傳統CPR進行了一定的對比。二維問題中直接基于單元尺度計算的CFL數，SCFV-GKS取為0.2，CRP-GKS以及傳統CPR均取0.1，三維問題中CFL數取值為0.05。

2.1 可壓縮Couette流動

考察在兩無限長平行平板之間的流動，上板溫度為T1= 1，運動速度為U1= 0.5，相應的馬赫數為Ma=0.5，下板靜止且絕熱。雷諾數設為Re=500。黏性系數μ與溫度呈線性關系μ=μ1T/T1，普朗特數為Pr=1。為了簡單起見，邊界條件按照解析解給定。需要說明的是，雖然流動定常，這里仍按非定常顯式推進，計算至足夠長的時間(t=300)后評估各格式所得結果的誤差與所用CPU時間。圖4給出了速度的2-范數誤差隨網格尺度變化的曲線。其中傳統CPR的無黏通量采用HLLC格式，黏性通量采用BR2格式，并且結合四步R-K方法進行時間推進。可以看出所有格式都達到了設計的精度階數，絕對誤差主要受重構階數影響。相比于三階格式，四階格式具有顯著更小的絕對誤差，并且隨著網格加密，絕對誤差下降得更快。

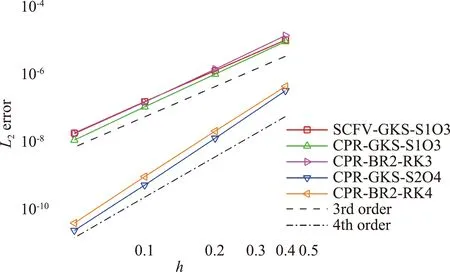
圖4 可壓縮Couette流動：速度誤差隨網格尺度的變化

為進一步考察格式的計算效率，圖5給出了絕對誤差隨計算所用CPU時間變化的曲線。雖然在相同網格尺度下，四階格式的計算量大于三階格式，但由于絕對誤差明顯更小，因此四階格式相比于三階格式具有明顯的效率優勢。對于傳統CPR，雖然傳統Riemann求解器的計算量較小，但在黏性問題中還需要額外處理黏性項，并且由于需要更多的子步，因此總的計算量與CPR-GKS相當。總之，基于CPR框架發展的兩步四階GKS具有最顯著的優勢。需要指出的是，本算例為光滑流動問題，因此沒有施加限制器。對于高速流動問題，施加限制器往往帶來較大的計算量，由于CPR-GKS能夠采用更少的子步數達到高階時間精度，因此其計算效率相比于傳統CPR還能夠進一步提高。此外，考慮到三階CPR-GKS可以比四階格式取更大的CFL數，此時效率會有一定的提升，但仍然顯著低于四階格式。不同格式CFL數取值大小的影響仍有待進一步研究。

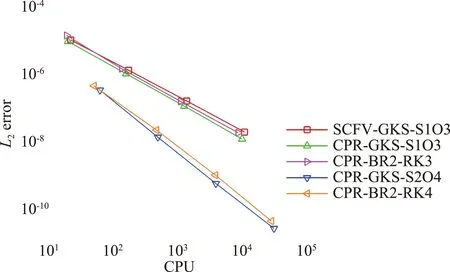
圖5 可壓縮Couette流動：速度誤差隨CPU時間的變化

2.2 雙馬赫反射

馬赫數Ma=10的正激波經過30°斜坡形成的雙馬赫反射是典型的二維強激波問題，可用于驗證格式的穩健性和激波捕捉能力。初始流場為:

計算時間為t=0.2，網格尺度為h=1/160。圖6給出了不同格式計算得到的三波點附近的密度等值線圖，其中包含30條在2.0～22.5之間均勻分布的密度等值線。可以看出，兩步四階CPR-GKS的計算結果最好，激波的分辨率最高，并且在滑移線上捕捉到了一系列小尺度渦結構。相比于單步三階CPR-GKS，單步三階SCFV-GKS在滑移線上捕捉到的渦結構更加明顯，但間斷略顯更寬。需要注意的是，與文獻[45]不同，本文的三階CPR-GKS由于在間斷區域結合了SCFV，每個單元內包含了更多的內自由度，因此對間斷的分辨率比SCFV-GKS更高。但是，兩者在子單元上采用的限制器是不同的：CPR-GKS采用的是二階TVD限制器，而SCFV-GKS則是HR-WENO，因此在滑移線附近，由于部分單元被標記為間斷單元，高階限制器使得SCFV-GKS得到的渦結構更加明顯。計算結果表明三種高精度GKS都能夠在激波捕捉中兼具高分辨率和強穩健性，并且兩步四階CPR-GKS的優勢更加明顯。

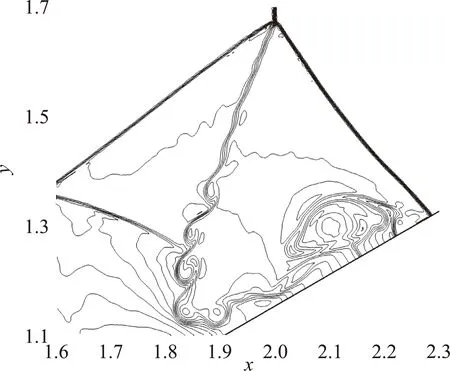
(a) 單步三階SCFV-GKS

圖7給出了兩步四階CPR-GKS計算得到的密度等值線的全局視圖，斜激波下方的等值線也比較光滑，說明格式能夠有效抑制數值振蕩。圖8進一步給出了由兩步四階CPR-GKS計算得到的馬赫桿附近的密度等值線，且同時展示了主單元和子單元的分布。可以看出激波厚度被成功限制在主單元的尺度內，因此能夠實現子單元尺度上的激波捕捉，驗證了CPR/SCFV混合算法對間斷的高分辨率。

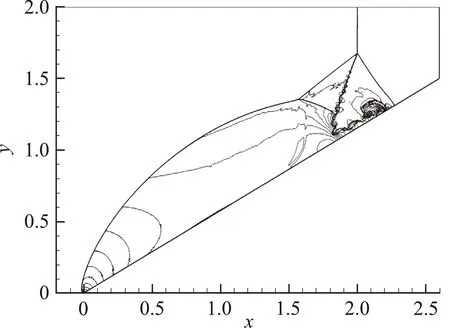
圖7 雙馬赫反射：密度等值線的全局視圖(t=0.2)，兩步四階CPR-GKS

圖8 雙馬赫反射：馬赫桿附近的等值線(t=0.2)，兩步四階CPR-GKS

2.3 三維超聲速圓球繞流

超聲速來流繞過圓球時，流場中包含復雜的波系和旋渦結構，對于數值方法具有較大的挑戰性。來流馬赫數取為Ma=1.2，雷諾數為Re=1000。計算網格如圖9所示，共88 128個單元，圓球表面附近的法向最小網格尺度為0.0365，拉伸率約為1.15，圓球表面為無滑移絕熱壁。

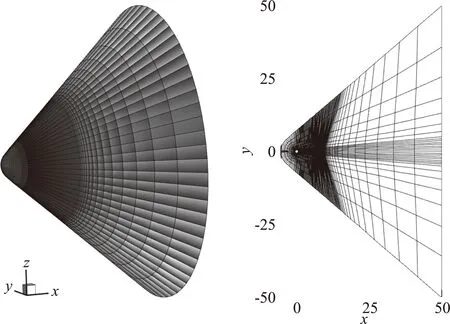
圖9 三維超聲速圓球繞流：計算網格

圖10給出了t=400的瞬時密度分布云圖，其中可以看到圓球前面的弓形激波、后部的膨脹波及流動分離形成的回流區，以及回流區末端的再壓縮波。在尾跡區則可以觀察到有大尺度的渦脫落。圖11給出了t=400 的瞬時Q判據等值面圖，其中Q=0.001，并以馬赫數著色。從圖中可以看到，四階CPR-GKS清晰地捕捉到了尾跡區的渦結構，且流場存在明顯的對稱面。圖12給出了阻力系數隨時間變化的曲線，可以看出流動結構的演化過程仍然具有明顯的周期性，但此時已出現較小的隨機擾動。由阻力系數曲線得到的頻譜如圖13所示，可以觀察到兩個主導的頻率分別為0.039 和0.145，此外還存在幾個更小的峰值頻率，并且都集中在低頻區域。統計得到的阻力時均值為1.055，計算結果與Nagata等給出的結果1.054吻合得較好[47]。

圖10 三維超聲速圓球繞流：密度分布云圖(t=400)

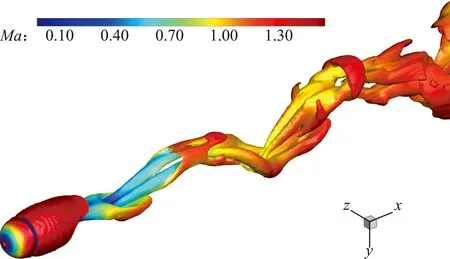
圖11 三維超聲速圓球繞流：Q判據等值面圖(t=400)

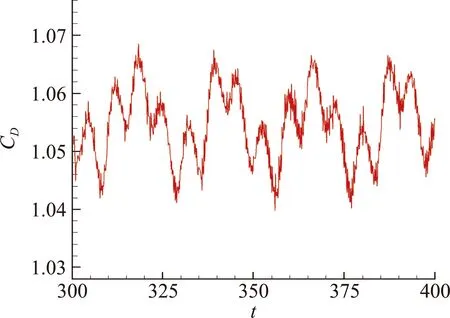
圖12 三維超聲速圓球繞流：阻力系數隨時間變化的曲線

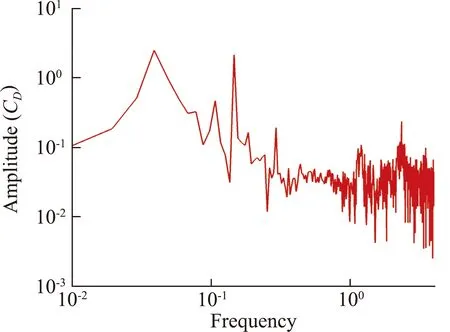
圖13 三維超聲速圓球繞流：阻力頻譜

3 結 論

本文介紹了近年來課題組在非結構網格高效高精度氣體動理學格式上的研究進展。利用介觀GKS通量求解器，結合基于內自由度的高效緊致重構方法，發展了單步時空三階精度的SCFV-GKS和CPR-GKS，以及時空四階精度的CPR-GKS。利用GKS通量的多維空間分布，結合單元內部的連續分布，減少通量的計算量，同時結合通量的時間演化特性減少或消除時間方向的推進子步，從而有效提高了計算效率。混合光滑區CPR和間斷區域SCFV發展的兩步四階CPR-GKS，很好地兼顧了高精度、高分辨率和強穩健性。進一步結合曲邊網格技術發展了六面體網格上的四階CPR-GKS，有效增強了格式在復雜流動中的實用性能。

在此基礎上，通過典型算例對幾種格式進行驗證和對比分析，考察了不同格式的精度、效率以及激波捕捉性能。結果表明，其中結合SCFV的兩步四階CPR-GKS具有顯著的優勢。基于氣體動理論的GKS求解器包含豐富的時空演化信息，充分利用這些信息，結合高效的緊致重構方法，能夠發展兼具高精度、高效率和強穩健性的新型數值方法，為新一代CFD軟件開發提供有力支撐。

在后續的研究工作中，還需要對高階GKS在三維流動問題，特別是包含強激波的流動問題中的計算性能做進一步的驗證。同時，本文涉及到的均為顯式格式，為增強對實際工程問題的模擬能力，有必要開展隱式高精度格式研究。此外，為模擬工程實際中面臨的高雷諾數湍流問題，可以基于拓展BGK方程的跨尺度演化解發展新型的可壓縮湍流多尺度模擬方法，并應用于典型高雷諾數工程湍流精細模擬。

致謝:感謝清華探索100高性能計算平臺、并行科技高性能計算支持服務為本文工作提供部分計算機時。