部署retro-GEO巡視器的月球借力飛行軌道分析
賀波勇,馬鵬斌,杜衛(wèi)兵,李恒年
1. 西安衛(wèi)星測(cè)控中心 宇航動(dòng)力學(xué)國(guó)家重點(diǎn)實(shí)驗(yàn)室,西安 710043
2. 西北工業(yè)大學(xué) 航天學(xué)院,西安 710072
月球引力輔助甩擺力學(xué)原理最早可追溯至1687年牛頓的數(shù)學(xué)建模描述。Apollo任務(wù)中繞月自由返回軌道便是人類利用月球引力輔助甩擺提高航天員安全性的著名載人航天實(shí)踐活動(dòng)[1]。1990年,日本發(fā)射Hiten航天器,進(jìn)行了雙月旁轉(zhuǎn)向飛行試驗(yàn)[2]。1998年,休斯公司利用月球甩擺實(shí)現(xiàn)亞洲三號(hào)衛(wèi)星挽救轉(zhuǎn)移軌道控制,成就人類第一次成功挽救人造衛(wèi)星的航天傳奇[3-4]。2000年,國(guó)內(nèi)學(xué)者曾國(guó)強(qiáng)等[5-6]基于雙二體圓錐曲線拼接模型研究了利用月球甩擺從地球高緯度地區(qū)發(fā)射地球靜止軌道(geostationary Earth orbit, GEO)和逆行衛(wèi)星軌道設(shè)計(jì)問(wèn)題,表明利用月球借力發(fā)射逆行衛(wèi)星可以節(jié)約一定能量,但采用簡(jiǎn)化動(dòng)力學(xué)模型不能反映該類軌道參數(shù)屬性。羅宗富[7]研究了雙月旁轉(zhuǎn)向軌道存在性力學(xué)機(jī)理與建模設(shè)計(jì)方法,一定角度上闡明了月球借力飛行的參數(shù)敏感性力學(xué)原理。彭祺擘[8]通過(guò)地月轉(zhuǎn)移軌道一階偏導(dǎo)數(shù)矩陣(狀態(tài)傳播矩陣條件數(shù))分析了月球?qū)壍绤?shù)的快速非線性放大作用。隨著GEO衛(wèi)星數(shù)量指數(shù)增長(zhǎng),廢棄衛(wèi)星及碎片引起的GEO資產(chǎn)安全性問(wèn)題日益嚴(yán)峻[9]。1984年,Oberg[10]開拓性地提出了retro-GEO(retrograde GEO)概念,并指出利用月球借力飛行部署該類軌道可以節(jié)約發(fā)射能耗。2001年,Kawase[11-12]提出利用retro-GEO監(jiān)測(cè)GEO軌道帶碎片構(gòu)想。Aravind等[13]也通過(guò)簡(jiǎn)單的幾何軌道模型比較了幾種retro-GEO轉(zhuǎn)移方案導(dǎo)致衛(wèi)星剩余壽命的差別,但求解的retro-GEO軌道遠(yuǎn)低于GEO高度。可見(jiàn),retro-GEO軌道可對(duì)GEO帶全部資產(chǎn)每12 h巡視預(yù)警一次。但目前關(guān)于繞月飛行軌道設(shè)計(jì)方法模型精度不足,設(shè)計(jì)方法對(duì)參數(shù)敏感性高,且并未求解出符合要求的理想月球借力飛行軌道,也未對(duì)該類軌道參數(shù)屬性進(jìn)行分析。
1 問(wèn)題背景
1.1 GEO資產(chǎn)安全性嚴(yán)峻
GEO軌道周期與地球自轉(zhuǎn)周期相同,星下點(diǎn)覆蓋區(qū)域穩(wěn)定不變。許多導(dǎo)航、遙感、數(shù)據(jù)中繼、氣象、海洋監(jiān)測(cè)和國(guó)土資源監(jiān)測(cè)等重要衛(wèi)星都部署在GEO軌道。由于GEO受攝動(dòng)位置漂移的安全域限制和衛(wèi)星數(shù)目指數(shù)性增長(zhǎng),幾十年來(lái),很多GEO重要位置都是多顆衛(wèi)星共位控制而存在[14],加之火箭末級(jí)殘骸、失效衛(wèi)星及空間碎片等,GEO軌道相當(dāng)擁擠。
2014年7月28日和2016年8月19日,美國(guó)分別以一箭雙星方式成功發(fā)射GSSAP-1/2和GSSAP-3/4(geosynchronous space situational awareness program, GSSAP)4顆GEO軌道衛(wèi)星,可通過(guò)升高或降低軌道高度對(duì)GEO資產(chǎn)進(jìn)行鄰域碎片預(yù)警,但軌道機(jī)動(dòng)成本大大限制了巡視范圍[15]。
1.2 西向發(fā)射條件不具備
如果直接西向發(fā)射部署retro-GEO,存在2個(gè)難題:
1)一般衛(wèi)星均采用東向發(fā)射方式入軌,西向發(fā)射火箭一、二級(jí)殘骸落點(diǎn)均不是常規(guī)無(wú)人落點(diǎn)區(qū)域,可能是人口密集、甚至境外區(qū)域,可能給人民生命和財(cái)產(chǎn)安全帶來(lái)隱患,還可能引起外交糾紛和技術(shù)泄露風(fēng)險(xiǎn)。
2)東向發(fā)射可以利用成熟地面測(cè)控站行精確測(cè)控,而西向發(fā)射沒(méi)有成熟測(cè)控站支持。
1.3 月球探測(cè)器技術(shù)成熟
月球是地球唯一的天然衛(wèi)星,也是迄今為止人造探測(cè)器造訪最多的天體。特別是2018年5月、12月中國(guó)分別發(fā)射的嫦娥4號(hào)中繼星和探測(cè)器聯(lián)合月球背面探測(cè)任務(wù)[16-17],經(jīng)過(guò)數(shù)十個(gè)月晝?cè)乱谷栽诠ぷ鳎砻髁酥袊?guó)通過(guò)嫦娥任務(wù)已成熟掌握月球探測(cè)器發(fā)射、精密軌道確定和繞月變軌等技術(shù)。
2 借力飛行軌道描述與建模設(shè)計(jì)
2.1 借力飛行軌道描述
retro-GEO相對(duì)于地球固連坐標(biāo)系飛行周期約為12 h(也可略高或略低于GEO),每個(gè)周期可對(duì)GEO空間資產(chǎn)遍歷巡視和鄰域安全預(yù)警,如圖 1 所示。
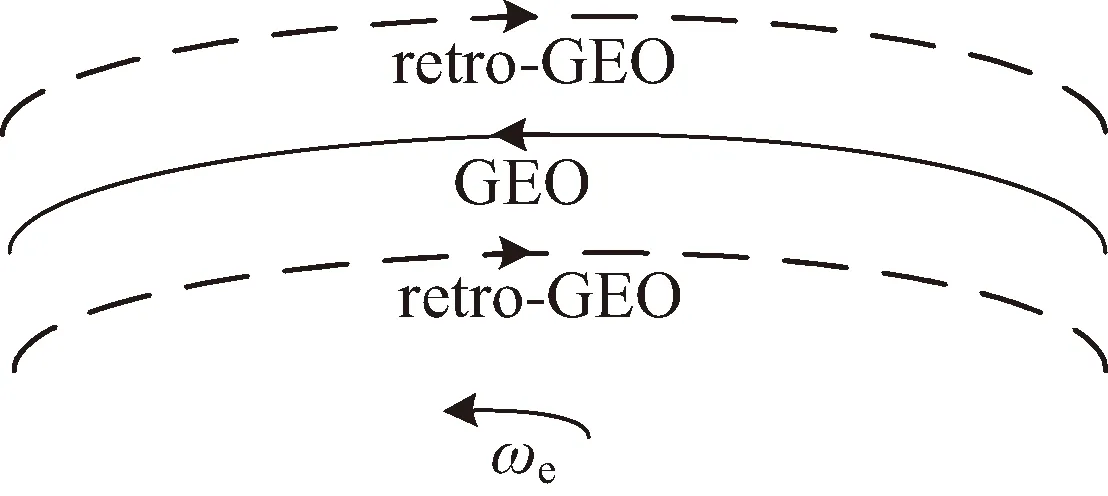
圖 1 retro-GEO示意
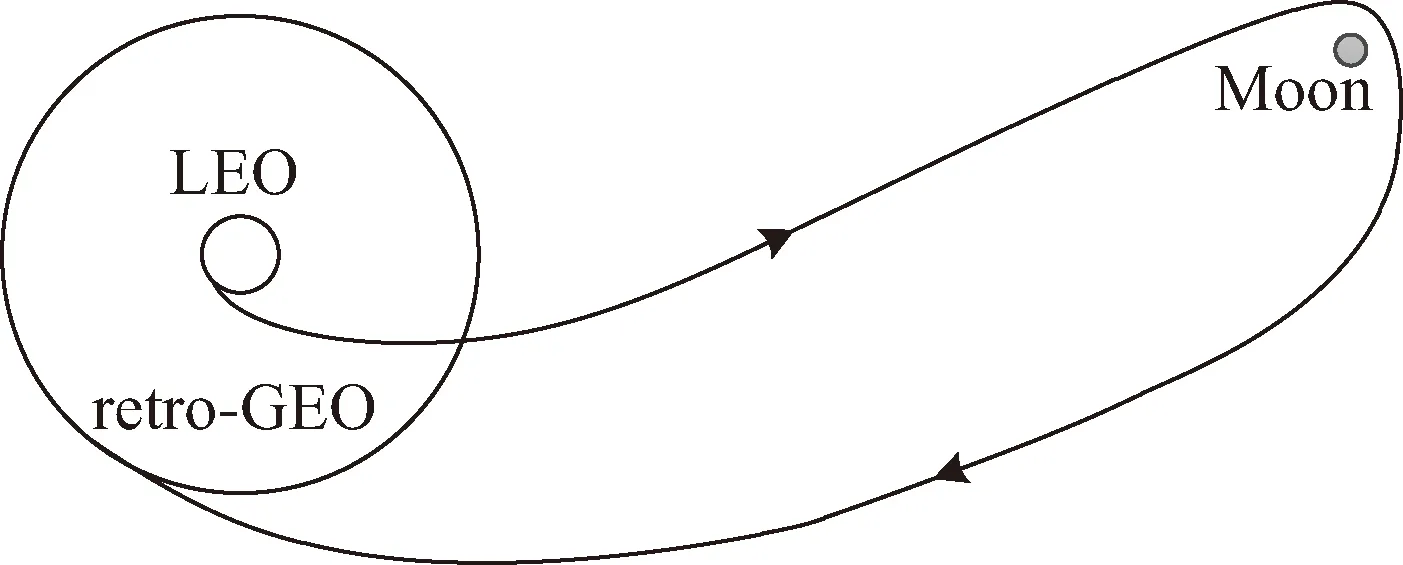
圖 2 部署retro-GEO巡視器的月球借力飛行軌跡示意
如圖 2 所示,利用月球借力飛行部署retro-GEO巡視器飛行軌跡是指從近地停泊軌道(low Earth orbit, LEO)切向施加一次脈沖,進(jìn)入地月轉(zhuǎn)移段,利用月球引力輔助甩擺后返回地球附近,近地距與GEO高度相同(可略高或略低),相對(duì)于地心J2000.0坐標(biāo)系傾角為180°,在近地點(diǎn)施加一次切向脈沖減速制動(dòng)形成retro-GEO巡視軌道。
(1)約束條件
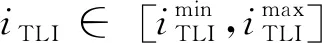
(2)設(shè)計(jì)目標(biāo)
從LEO出發(fā)至retro-GEO需要兩次制動(dòng)速度脈沖,設(shè)ΔvTLI和ΔvRGI(下標(biāo)“RGI”表示retro-GEO insertion,逆行GEO捕獲)分別為從LEO加速出發(fā)的速度增量和月球甩擺返回地球至GEO高度的減速制動(dòng)速度增量。軌道設(shè)計(jì)時(shí)希望在滿足約束情況下,軌道制動(dòng)燃料消耗小,便于攜帶更大有效載荷,即
一、本刊設(shè)有專家論壇、述評(píng)、論著、學(xué)術(shù)交流、專題筆談、綜述、講座、臨床病理(例)討論、教學(xué)園地、問(wèn)題解答、臨床研究、病例報(bào)告、誤診誤治、技術(shù)改進(jìn)等欄目,接受全國(guó)各地來(lái)稿。
Jmin=ΔvTLI+ΔvRGI
(1)
2.2 軌道設(shè)計(jì)建模
(1)軌道動(dòng)力學(xué)模型
在繞月飛行軌跡參數(shù)初步設(shè)計(jì)分析時(shí),通常會(huì)使用圓錐曲線拼接模型和圓型限制性三體模型(circular restricted 3 body problem, CR3BP)等簡(jiǎn)化軌道動(dòng)力學(xué)模型。前者因其半解析特性,在Apollo任務(wù)分析中廣泛運(yùn)用,但在計(jì)算飛行時(shí)間較長(zhǎng)的地月轉(zhuǎn)移軌道設(shè)計(jì)問(wèn)題中誤差很大,甚至得到錯(cuò)誤的結(jié)論[18-20]。而后者全時(shí)段同時(shí)考慮地月引力,結(jié)論可信度高,但需數(shù)值積分運(yùn)算。
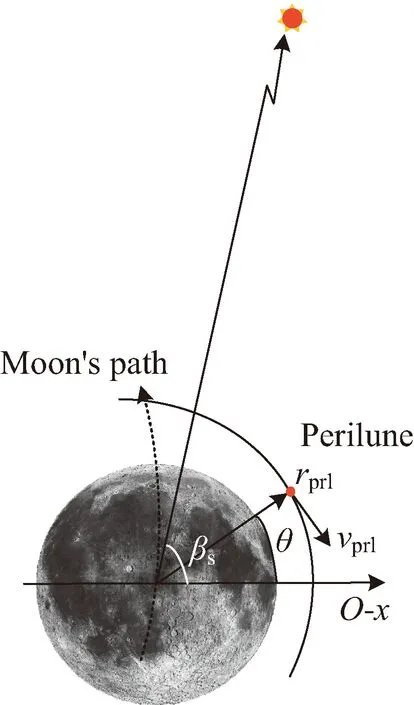
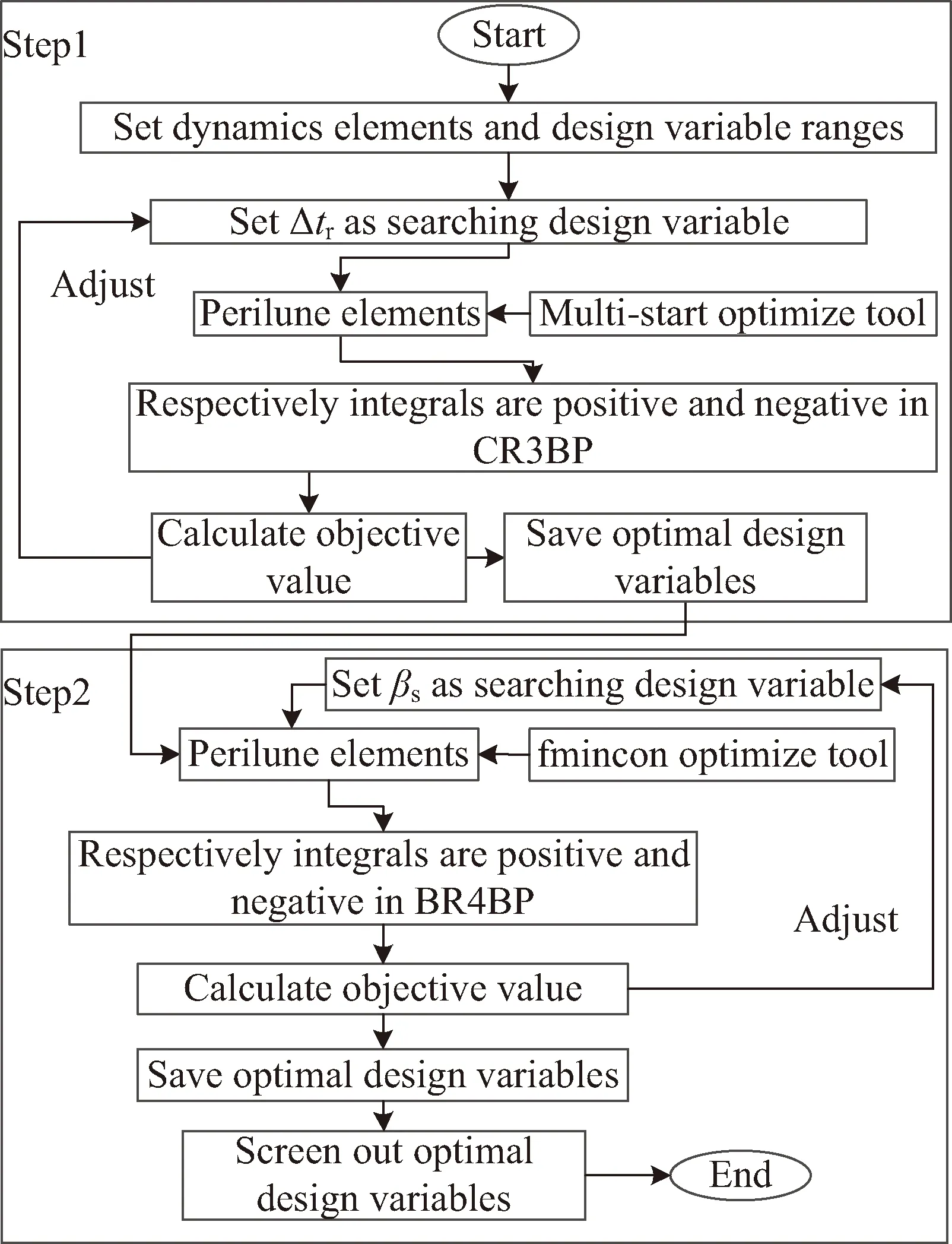
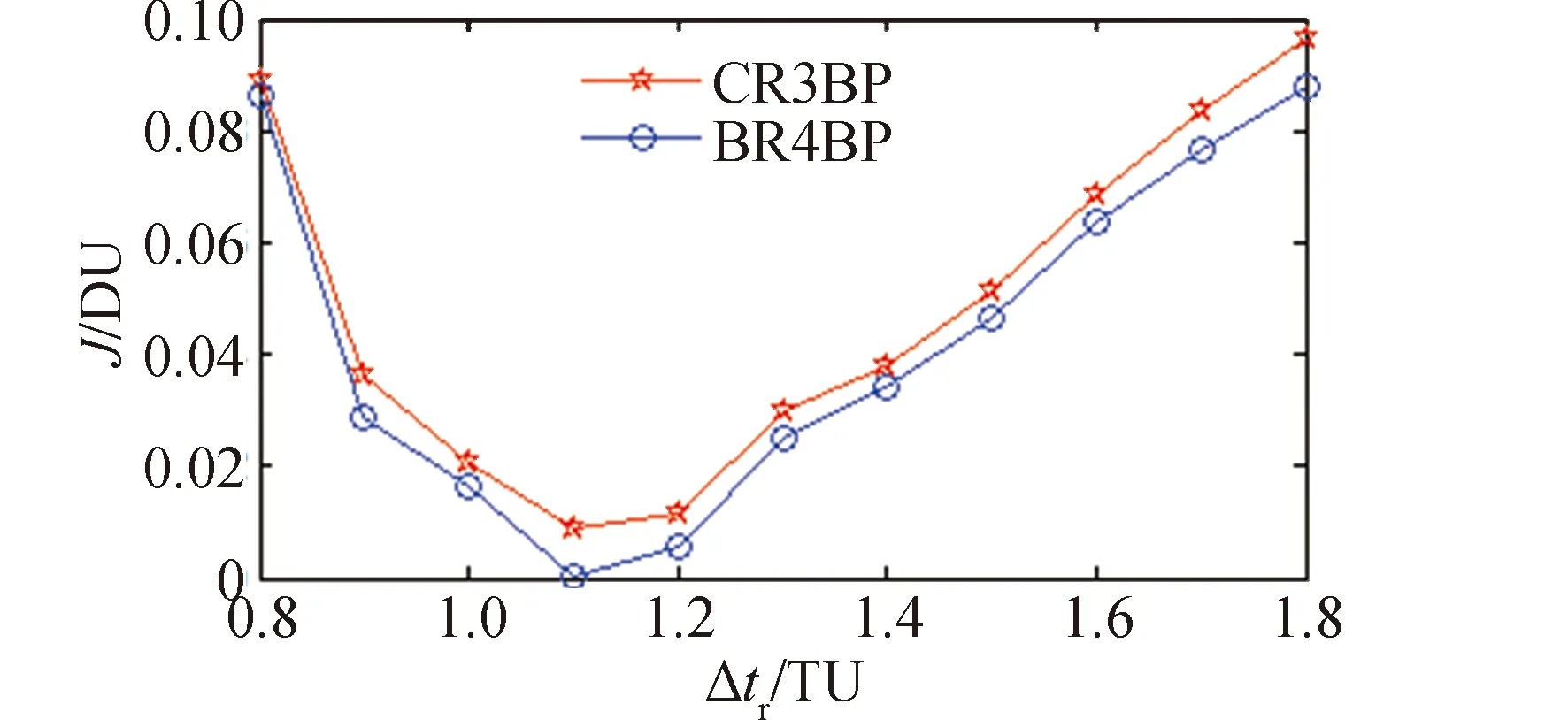
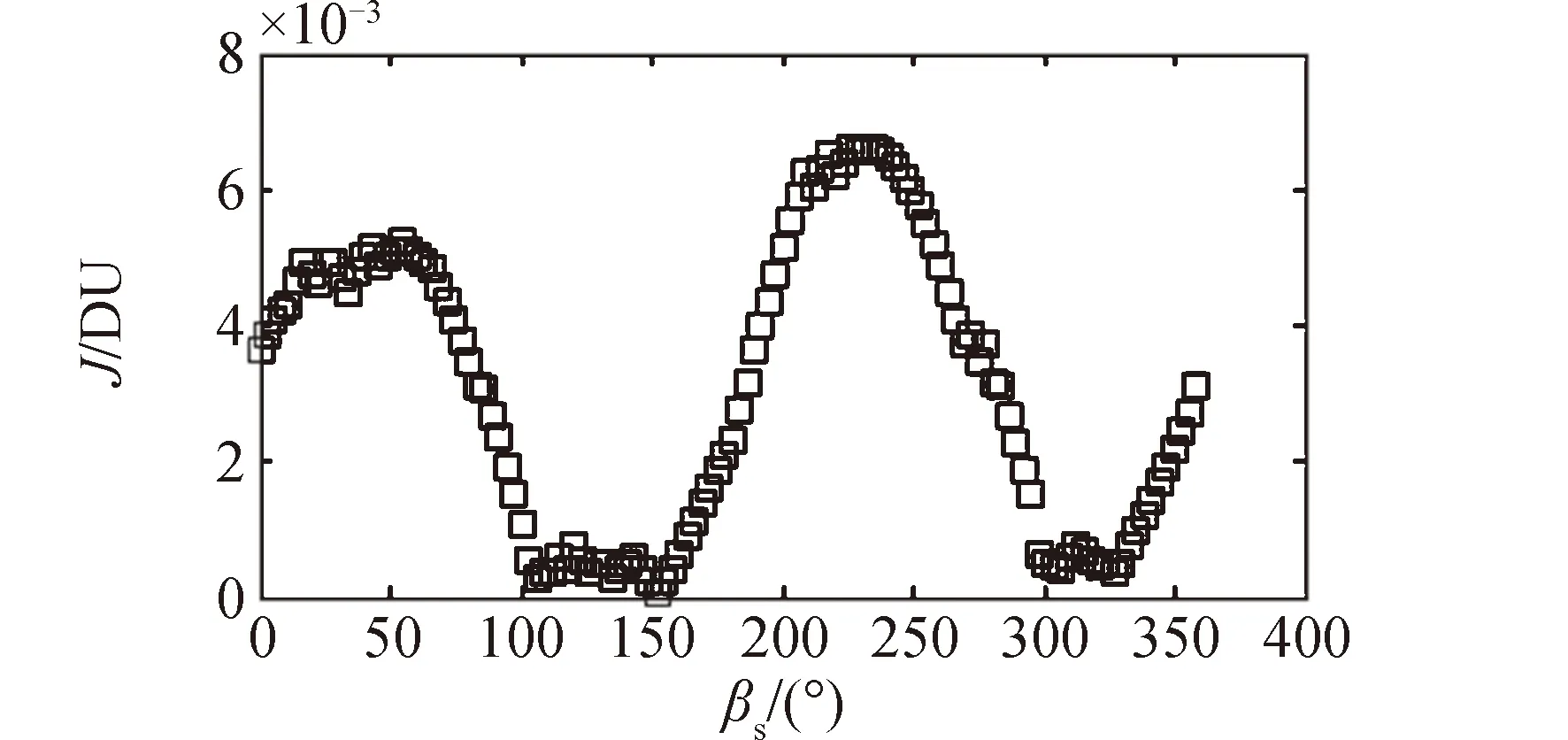
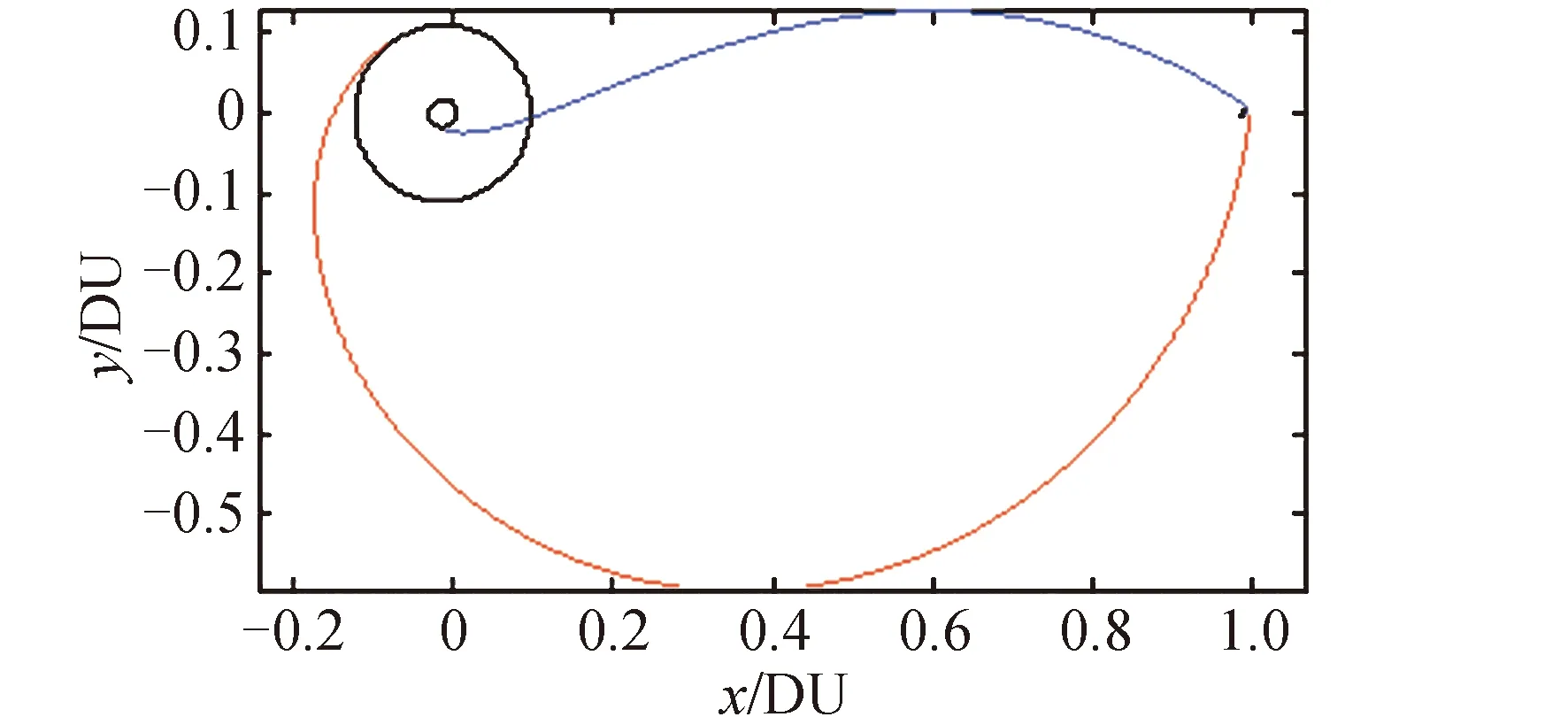
CR3BP是指存在兩個(gè)主天體P1和P2,對(duì)應(yīng)質(zhì)量分別為m1和m2,相互繞其公共質(zhì)心勻速圓周運(yùn)動(dòng),研究質(zhì)量為m?m2 這里引入等效勢(shì)能函數(shù) 表1 考慮太陽(yáng)攝動(dòng)地月空間引力場(chǎng)常數(shù)[21] 由于地月轉(zhuǎn)移軌道在月球影響球附近受到的地球和月球中心引力均小于6×10-3m/s2,這時(shí)太陽(yáng)中心引力攝動(dòng)約為6×10-3m/s2[22],應(yīng)在CR3BP基礎(chǔ)上考慮第四體P3,對(duì)于地月系統(tǒng)而言,即考慮太陽(yáng)攝動(dòng)的雙圓限制性四體模型(bi-circular restricted 4 body problem, BR4BP)更接近真實(shí)的地月空間引力環(huán)境。由于白道面與黃道面僅相差約5°,簡(jiǎn)化認(rèn)為是日地月處于同平面。雙圓是指地月圍繞其公共質(zhì)心做圓周運(yùn)動(dòng)和地月公共質(zhì)心圍繞太陽(yáng)也做圓周運(yùn)動(dòng)的假設(shè)。第三體P在平面內(nèi)的動(dòng)力學(xué)方程為 等效勢(shì)能函數(shù) t時(shí)刻太陽(yáng)相對(duì)于O-x軸的相位角為ωst,對(duì)應(yīng)的位置為(ρcos(ωst),ρsin(ωst)。此時(shí),第三體探測(cè)器P與太陽(yáng)距離為: (2) 軌道設(shè)計(jì)模型 如文獻(xiàn)[8]所述,月球借力飛行后,地月轉(zhuǎn)移軌道狀態(tài)傳播矩陣條件數(shù)快速增大。對(duì)于部署Retro-GEO巡視器軌道而言,如果以TLI時(shí)刻飛行狀態(tài)為設(shè)計(jì)變量,勢(shì)必增加了軌道設(shè)計(jì)變量的敏感性和設(shè)計(jì)難度。本文提出以近月點(diǎn)時(shí)刻飛行狀態(tài)為設(shè)計(jì)變量,分別瞄準(zhǔn)匹配近地出發(fā)和繞月返回地球段約束條件,完成軌道設(shè)計(jì)。如圖3所示,設(shè)近月點(diǎn)時(shí)刻太陽(yáng)相對(duì)地月連線角為βs,月心距為rprl,近月點(diǎn)相對(duì)于地月連線角為θ,近月點(diǎn)速度大小為vprl,則可完全確定一條月球借力飛行空間軌跡。 圖 3 近月點(diǎn)設(shè)計(jì)變量 以該時(shí)刻狀態(tài)分別逆向和正向數(shù)值積分,可以同時(shí)計(jì)算地月轉(zhuǎn)移飛行段和月球借力后返回地球段軌道參數(shù)。在實(shí)際計(jì)算時(shí),并不知道一組近月點(diǎn)參數(shù)描述的月球借力飛行軌跡的近地出發(fā)時(shí)刻和繞月返回地球時(shí)刻。這時(shí)需要將逆向數(shù)值積分到近地出發(fā)時(shí)刻的飛行時(shí)長(zhǎng)和正向數(shù)值積分到返回地球近地點(diǎn)時(shí)刻,分別參數(shù)化為Δtd和Δtr。由于文獻(xiàn)[5,13]都沒(méi)有成功求解嚴(yán)格滿足近地出發(fā)和繞月返回Retro-GEO嚴(yán)格要求的轉(zhuǎn)移軌道,本文設(shè)計(jì)軌道時(shí),先不把式(1)所示的兩次脈沖和最小作為優(yōu)化目標(biāo)函數(shù),而需將慣性參考系中近地切向加速出發(fā)條件和出發(fā)時(shí)刻地心距、返回地球近地點(diǎn)時(shí)刻和返回時(shí)刻地心距都作為優(yōu)化目標(biāo)函數(shù),則軌道設(shè)計(jì)轉(zhuǎn)化為優(yōu)化問(wèn)題求解的模型為 式中,由于采用歸一化的CR3BP和BR4BP模型,月球公轉(zhuǎn)角速度為1,將近地出發(fā)和返回地球近地點(diǎn)約束統(tǒng)一未加權(quán)作為目標(biāo)函數(shù);rTLI、vTLI、rRGI和vRGI為慣性參考系中位置和速度矢量,而式(2)和式(4)中位置和速度均為會(huì)合坐標(biāo)系中變量,相互轉(zhuǎn)化關(guān)系如下: (3)軌道動(dòng)力學(xué)模型延拓策略 為了求解式(7)軌道設(shè)計(jì)問(wèn)題,先不考慮太陽(yáng)攝動(dòng),利用較簡(jiǎn)單的CR3BP軌道動(dòng)力學(xué)模型。即設(shè)計(jì)變量不考慮βs,并將Δtr設(shè)置為變量,利用MATLAB集成優(yōu)化工具包中Multi-start求解(在優(yōu)化變量區(qū)間內(nèi)隨機(jī)給出多個(gè)初值,以每個(gè)初值局部搜索),如圖4所示。 圖 4 延拓求解策略流程 再將CR3BP模型下的軌道設(shè)計(jì)變量當(dāng)作設(shè)計(jì)變量初值,在某個(gè)Δtr固定值情況下,將βs在0~2π區(qū)間內(nèi)遍歷搜索,利用Matlab集成優(yōu)化工具包中的fmincon求解,在結(jié)果中選出目標(biāo)函數(shù)值最小的βs對(duì)應(yīng)設(shè)計(jì)變量作為最優(yōu)設(shè)計(jì)變量。兩步延拓求解策略流程。 為了充分利用月球引力作用,設(shè)置歸一化的近月距rprl∈[4.777,5.777]×10-3,參考文獻(xiàn)[23],設(shè)置近月點(diǎn)速度vprl∈[2.3,2.7],近月點(diǎn)至近地出發(fā)逆向飛行時(shí)長(zhǎng)Δtd∈[-0.8,-0.5],θ∈[-π,π]。計(jì)算得到CR3BP模型和BR4BP模型最優(yōu)目標(biāo)函數(shù)隨Δtr∈[0.8,1.8]變化情況如圖5所示。 圖 5 最優(yōu)目標(biāo)函數(shù)變化 可見(jiàn),只有當(dāng)Δtr≈1.1 TU時(shí)存在最優(yōu)解。當(dāng)Δtr=1.1TU時(shí),近月點(diǎn)時(shí)刻太陽(yáng)處于方位對(duì)式(7)中目標(biāo)函數(shù)影響如圖6 所示。可知,太陽(yáng)位于最優(yōu)攝動(dòng)方向(βs≈152°),才可以找到目標(biāo)函數(shù)值最小的情況(式(7)中J≤7.0×10-5),此時(shí)月地段實(shí)際飛行時(shí)長(zhǎng)約為114.79 h,該條軌道歸一化后的平面軌跡如圖7所示。 圖 6 太陽(yáng)不同方位攝動(dòng)影響 圖 7 部署retro-GEO巡視器的月球借力飛行軌跡 由圖6可知,式(7)目標(biāo)函數(shù)值處于較小值要求太陽(yáng)位于的攝動(dòng)方向分布范圍有限,即日地月相對(duì)運(yùn)動(dòng)引起的發(fā)射窗口較小。說(shuō)明該類軌道存在條件較為苛刻,也從另一個(gè)角度解釋了文獻(xiàn)[5,13]沒(méi)有成功求解該類軌道的原因。 基于CR3BP和BR4BP模型,提出了利用近月點(diǎn)狀態(tài)為設(shè)計(jì)變量的部署retro-GEO巡視器的月球借力飛行軌道求解方法,仿真算例表明: 1)以近月點(diǎn)狀態(tài)為設(shè)計(jì)變量可有效減弱軌道狀態(tài)傳播矩陣的非線性快速增大效果,便于利用通用局部梯度優(yōu)化工具求解,延拓策略可為復(fù)雜問(wèn)題提供較為精確的設(shè)計(jì)變量初值,便于快速收斂; 2)部署retro-GEO的月球借力飛行軌道存在條件苛刻,只有近月點(diǎn)至返回地球近地點(diǎn)飛行時(shí)長(zhǎng)約為114.79 h,且太陽(yáng)處于最優(yōu)攝動(dòng)方向時(shí),才可以找到理論意義上目標(biāo)軌道。 本文揭示的該類軌道存在條件可為下一步求解該類軌道高精度軌道動(dòng)力學(xué)模型解提供設(shè)計(jì)變量初值參考。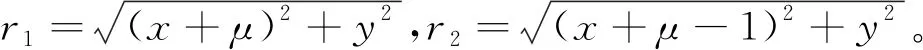

3 算例驗(yàn)證
4 結(jié)束語(yǔ)

