基于MATLAB 的碎紙片拼接復原技術研究
唐巧玲 陳 佳
(內江師范學院,四川 內江641100)
1 概述
碎紙片自動拼接技術是圖像處理和模式識別領域中一種典型的新型應用,通過掃描成像技術獲得一組被撕開的紙張的形狀和顏色,再由計算機獲取相應的信息,并通過計算機對這些紙張進行全自動或半自動復原的技術[1]。
本文主要研究由豎條型碎紙機粉碎的碎紙片,因此每個碎紙片的邊緣是齊整的,所以無法利用碎紙片的輪廓形狀得到有價值的信息,只能利用碎紙片邊緣的所承載的色彩信息,來獲取有價值的信息,再經過一系列的處理,進而實現碎紙片的拼接復原[6]。本文利用MATLAB 提取碎紙片圖片對象,將其看成一個集合,在水平方向對比兩個碎紙片的相似度,選出相似度最高的兩個碎紙片拼接成新的碎紙片,對已拼接完成的一側停止比較,只比較另一側,直至拼接完成為止。然后對計算機處理的結果進行分析,提高其匹配率[7-8]。
2 碎紙片拼接技術的原理
2.1 圖像預處理
碎紙片自動拼接復原技術是圖像處理和模式識別領域中的典型應用,這一項技術通過掃描與圖像提取技術來獲取碎紙片的顏色和形狀等有用的信息,之后再利用計算機對提取的信息進行進一步的處理,從而達到碎紙片的全自動復原或者半自動復原的目的。在碎紙片拼接復原過程中,最重要的就是圖像的預處理和碎紙片的匹配,圖像預處理就是把碎紙片轉化成計算機可以識別和處理的數據,而碎紙片匹配是在這些處理后的數據基礎之上進行的。
本文首先運用MATLAB 軟件對碎紙片做圖像預處理:調用函數imread 使圖片轉化成灰度矩陣,該灰度矩陣的每個元素為0 到255 的整數。不同的數字代表不同的灰度級或者亮度,其中數字0 表示黑色,數值255 表示白色,而每個矩陣中的各個數據表示其對應碎紙片的一個像素,這些數據就展示了碎紙片的數字特征信息,本文通過分析碎紙片提取出來的數字矩陣的灰度信息,發現矩陣的第一列和最后一列,然后將碎紙片邊緣轉化生成的數字特征信息進行處理,并對每個矩陣進行兩兩比較,就可以找出相鄰的碎紙片。
2.2 碎紙片拼接復原
為了可以更加方便的進行碎紙片拼接處理,計算出兩張碎紙片具體的邊緣相似度的數字,本文引入了差異度量,其具體公式如下:

其中:

當S 的值越小時,就說明兩個矩陣的兩列數據差值越小,也就說明這兩個碎紙片的相似度越高,其匹配度也就更高,進而選擇將這兩張碎紙片進行拼接,作為相鄰的碎紙片。
本文研究對縱切的碎紙片進行拼接復原的技術,主要是利用計算機自動拼接模型來對碎紙片邊緣進行拼接處理,并且考慮邊緣灰度,再分析差異度量,先找出最左端的碎紙片,再向右依次拼接成一個完整的圖片,然后輸出圖像。
3 基于縱切的中英文碎紙片復原技術研究
3.1 問題分析
對于單面僅縱切的碎紙片的情況,本文的碎紙片是來自同一印刷文件,并且都是規則的碎紙片,觀察左右兩側的邊緣發現有許多文字被切開,所以對碎紙片的拼接問題就轉化成將兩側被截斷的字符進行拼接的問題。本文在進行拼接時,選取碎紙片都是隨機的,在選取碎紙片之后,再將這個碎紙片與剩下的碎紙片進行邊緣信息相似度計算(差異化度量),然后比較這兩個碎紙片的邊緣信息相似度,選擇邊緣信息相似度最高的兩張圖片拼接成一個完整的字符。在進行邊緣匹配的時候,可能遇到有一張碎紙片的左側和一張碎紙片的右側為白色部分的情況,那么這兩張碎紙片就可能是整個文件的左右兩端的兩張碎紙片。
3.2 模型假設
假設所有碎紙片的大小都是一樣的,并且具有以下特點:
3.2.1 碎紙片的圖像是完好無損的;
3.2.2 碎紙片圖像只含中英文,不含有特殊符號;
3.2.3 碎紙片的文字未經過任何的旋轉;
3.2.4 碎紙片的切割方向都是垂直方向的;
3.2.5 碎紙片的形狀都是規則的且大小相同的幾何碎片。
對于本文所研究的碎紙片,轉化成的灰度矩陣可能出現的情況有以下三種:
(1)第一張碎紙片的灰度矩陣的第一列全為零;
(2)最后一張碎紙片的灰度矩陣的最后一列全為零;
(3)其他碎紙片的灰度矩陣的各個行列的值為0-255 的任意數值:
那么就可以根據這三種情況,通過計算機處理,將碎紙片進行自動拼接復原,這三種情況就分別對應原圖的第一張碎紙片,最后一張碎紙片和除第一張和第二張之外的其他碎紙片。
3.3 模型的建立和求解
3.3.1 模型的建立
本文利用MATLAB 軟件對碎紙片進行圖片預處理,將每個碎紙片轉化成一個1980×72 的灰度矩陣,矩陣里面的每個元素數值為0-255,0 表示黑色,255 表示白色,而圖片中的信息是文字信息,因為文字信息存在陰影部分,所以矩陣中出現了介于0到255 的數值元素[5]。本文將1980×72 的灰度矩陣命名為A,其類型如下所示:

因為灰度矩陣A 中的元素過多且數據過大,不利于比較,因此可以對灰度矩陣A 進行二值化處理,將矩陣A 轉化新的灰度矩陣,命名為B,其類型如下:

在進行拼接的時候,每個矩陣中的中間元素都是一個像素點,但在拼接只需要用到邊緣數據信息,也就是每個灰度矩陣的第一列和最后一列,只需要將這兩列進行兩兩比較,并計算出它們的差異化度量,選取匹配度最高的兩個碎紙片作為相鄰的碎紙片,后面再依次計算,從而實現碎紙片的復原[6-8]。
3.3.2 模型的求解
為了避免碎紙片的重復使用,所以需要在處理完灰度矩陣后,對每個灰度矩陣進行編號。在拼接過程中,需要先找出最左端的碎紙片作為第一張碎紙片,也就是第一列全為零的矩陣B的碎紙片,然后將此矩陣的第二列與剩下的矩陣的最后一列進行差異化度量值的計算,在差異化度量值中取最小值,即與它相似度最高的矩陣作為第二張碎紙片,按照這種方法,依次循環,直至拼接完成為止。碎紙片復原的的程序流程圖如圖1 所示。對碎紙片進行預處理,提取圖片的灰度矩陣,并將所有的碎紙片都轉化成灰度矩陣,并將這些矩陣都放入數組A 中。利用冒泡循環將所有的灰度矩陣進行二值化處理,如果矩陣中元素不等于255,就轉化成0,如果矩陣中的元素等于255,就轉化成1。然后判斷每個碎紙片的第一列元素是否為零,如果為零,就將其作為第一個碎紙片。將碎紙片矩陣的第一列和另一個碎紙片矩陣的最后一列比較,計算其差異化度量,并選取匹配度最高的碎紙片,作為兩個相鄰的碎紙片,其核心代碼如下:
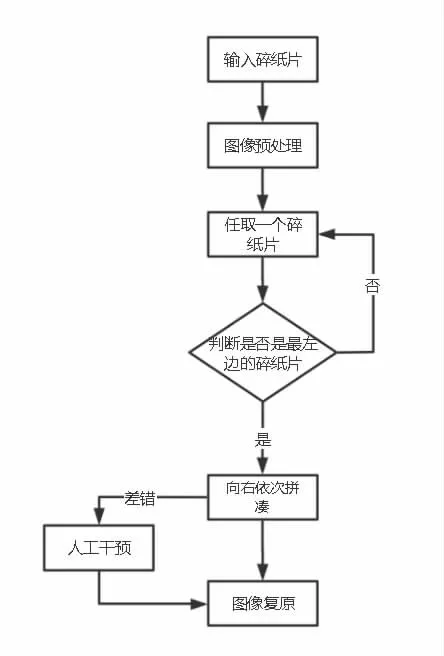
圖1 碎紙片復原流程圖
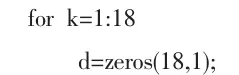

待所有碎紙片拼接完成之后,輸出碎紙片的正確順序和拼接復原之后的圖像。
4 實驗結果
對于本文采用的中文碎紙片和英文碎紙片,經過拼接復原,得到碎紙片的正確順序如表1 和表2 所示。

表1 中文碎紙片復原序列

表2 英文碎紙片復原序列
從得到的拼接復原結果可以看出,本文采用的拼接復原方法實現了中英文的縱切的規則碎紙片的拼接復原,可靠性較高。
結束語
本文基于MATLAB 平臺,構建每張碎紙片的灰度矩陣并將其進行二值化,通過計算矩陣之間的差異化度量值等相關系數,并根據相關系數的大小來判斷碎紙片匹配度的高低,以此找到相鄰的碎紙片,從而完成碎紙片的拼接復原。本文對于縱切的碎紙片拼接復原,準確率較高,人工干預較少,可靠性高。但對于其它粉碎方式的碎紙片或者不規則的碎紙片,本文建立的模型并不適用,需要另行研究。

