基于粒子群算法的LCLC諧振變換器優化設計

趙 斌 王 剛*② 宋婧妍② 劉雅琳

①(中國科學院空天信息創新研究院高功率微波源與技術重點實驗室 北京 100190)

②(中國科學院大學 北京 100039)

1 引言

空間行波管放大器(Traveling-Wave Tube Amplifier， TWTA)廣泛應用于雷達、電子對抗以及衛星導航等應用中，起到微波功率放大的作用[1]。空間行波管放大器由兩部分構成：電子功率調節器和空間行波管。電子功率調節器為空間行波管的正常工作提供合適的高電壓[2]，因此，電子功率調節器的效率將直接影響整個空間行波管放大器的效率[3，4]。提高電子功率調節器的效率，對于降低衛星上太陽能電池板的數量，降低發射重量，具有重要的意義。

當前，如圖1所示，電子功率調節器普遍采用2級結構：第1級為Buck變換器[5]，第2級為LCLC諧振變換器[6]。目前，由于Buck變換器已經得到了廣泛的研究，因此，本文主要研究LCLC諧振變換器[7，8]。第2級LCLC諧振變換器，將Buck變換器的輸出電壓，升壓為行波管所需要的高電壓，并提供電氣隔離的功能。然而，如圖1所示，LCLC諧振變換器具有4個諧振參數，Lr為變壓器漏感；Cs為串聯諧振電容；Lm為變壓器勵磁電感；Cp為并聯諧振電容(即變壓器寄生電容)，增加了LCLC諧振變換器總損耗優化的難度。因此，當前，LCLC諧振變換器的設計主要依賴經驗，無法對LCLC諧振變換器的總損耗進行優化。

近年來，粒子群優化設計算法在功率變換優化設計中得到了廣泛的應用[9]。粒子群優化算法從隨機解出發，通過適應度評價解的品質，并通過多次迭代搜索最優值求得最優解[10，11]，具有精度高優化以及收斂快等優點[12，13]。本文將粒子群優化設計算法應用到LCLC諧振變換器中，提出了一種基于粒子群優化設計算法的LCLC諧振變換器優化設計方法。該優化設計方法以LCLC諧振變換器的總損耗為優化設計的目標函數，通過粒子群優化算法，求得總損耗最低時的LCLC諧振變換器的諧振參數(Lr， Cs， Lm和Cp)。基于總損耗最低時的諧振參數，搭建LCLC諧振變換器，最終實現LCLC諧振變換器的高效率。

本文按照如下的思路展開：第2節通過對LCLC諧振變換器工作原理的分析，推導了LCLC諧振變換器總損耗的公式；第3節基于LCLC諧振變換器的總損耗公式，提出了基于粒子群優化算法的LCLC諧振變換器優化設計方法，并給出了例子；第4節基于第3節中的例子，搭建了優化設計的LCLC諧振變換器，并進行了一系列實驗，用于驗證本文提出的優化設計方法；第5節對本文進行了總結。

2 LCLC諧振變換器總損耗分析與計算

在本節中，基于LCLC諧振變換器的工作原理[14]，對LCLC諧振變換器的總損耗進行了計算。在空間行波管放大器的應用中，由于LCLC諧振變換器工作在零電流、零電壓條件下，因此，開關管無開通和關斷損耗。LCLC諧振變換器的損耗包含開關管驅動損耗、開關管的導通損耗、串聯諧振電容損耗、變壓器銅損、變壓器鐵損、變壓器介質損耗以及整流二極管損耗。下面將分別對各部分損耗進行計算，并推導得到LCLC諧振變換器的總損耗公式。

2.1 高壓整流二極管損耗

在LCLC諧振變換器中，為降低整流二極管損耗，采用碳化硅二極管，因此，反向恢復損耗可以忽略。高壓整流二極管的損耗為導通損耗，即

其中，PD為高壓整流二極管損耗，Vo為LCLC諧振變換器的輸出電壓，VD為高壓整流二極管的管壓降，Ro為變換器負載。

2.2 主開關管驅動損耗

主開關管的驅動損耗為

其中，Qg為門極驅動電荷，Vdr為開關管的驅動電壓，fs為LCLC諧振變換器的諧振頻率。

2.3 主開關管的導通損耗

由于在空間行波管放大器應用中，主開關管實現了零電壓、零電流導通和關斷，導通損耗和關斷損耗降為0。導通損耗為

其中，Irms為諧振電流有效值，Ron為主開關管的導通電阻。

結合諧振電流有效值的計算公式[14]，主開關管的導通損耗為

其中，Vo為LCLC諧振變換器輸出電壓，Ts為開關周期，Trs為Lr和Cs的諧振周期，Ro為負載，a為變壓器變比。

2.4 主變壓器銅損

由于LCLC諧振變換器工作在高頻條件下，引起變壓器繞組的鄰近效應和趨膚效應，從而加劇了變壓器的銅損。變壓器的銅損為

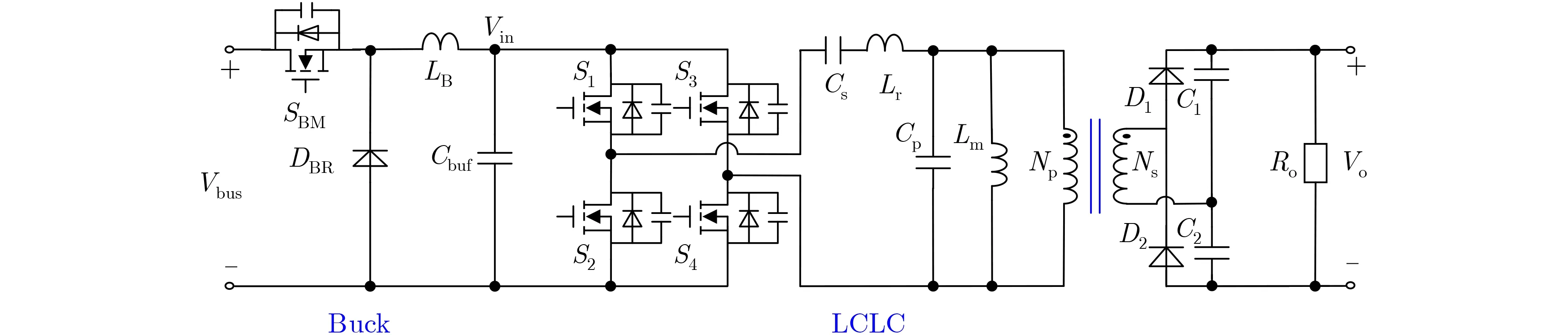
圖1 電子功率調節器的兩級結構

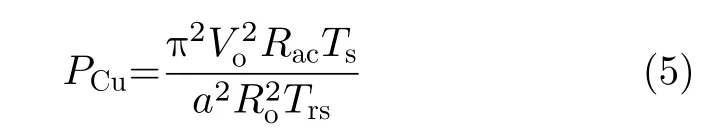
其中，Rac為變壓器的交流電阻。

2.5 主變壓器介質損耗

在空間行波管放大器的應用中，輸出電壓從數千伏到一萬多伏不等；此外，LCLC諧振變換器工作在高頻條件下，變壓器的寄生電容在每個開關周期都要進行充放電，從而引起介質損耗。主變壓器的介質損耗為[13]

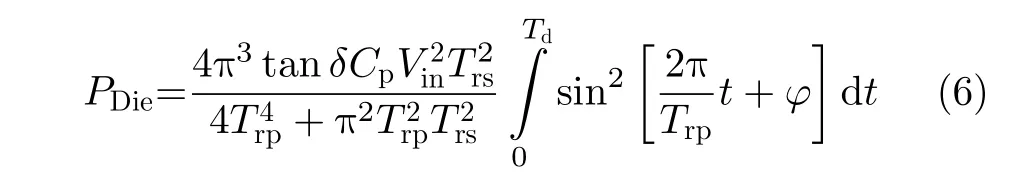
其中，δ為介質的損耗角，Trp為Lm和Cp的諧振周期，Td為死區時間，φ 為一常數。

2.6 變壓器磁芯損耗

變壓器在工作中，除具有銅損和介質損耗之外，磁芯也將產生損耗。在LCLC諧振變換器中，磁芯損耗為

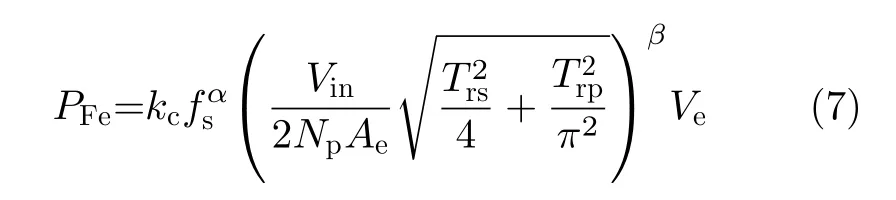
其中，kc，α，β為磁芯材料損耗參數，Ve為磁芯體積。

2.7 LCLC諧振變換器總損耗

結合式(1)—式(7)，得到變換器的總損耗為

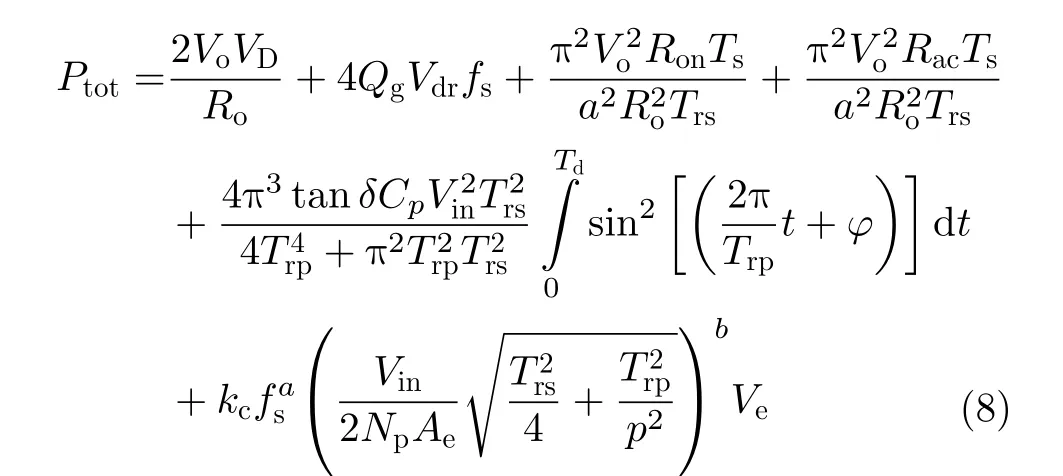
在接下來的優化設計中，將式(8)作為優化目標，進行LCLC諧振變換器的優化設計。

3 基于粒子群優化算法的LCLC變換器優化設計

由于在LCLC諧振變換器中具有4個諧振參數，即漏感、串聯諧振電容、變壓器勵磁電感以及變壓器寄生電容，因此，LCLC諧振變換器的優化設計比較困難。本文結合當前的人工智能算法和粒子群優化算法，提出了基于粒子群優化算法的LCLC變換器優化設計方法。

3.1 LCLC諧振變換器優化設計方法

基于粒子群優化算法的LCLC變換器優化設計方法的流程圖如圖2所示。優化設計算法分為以下幾步：

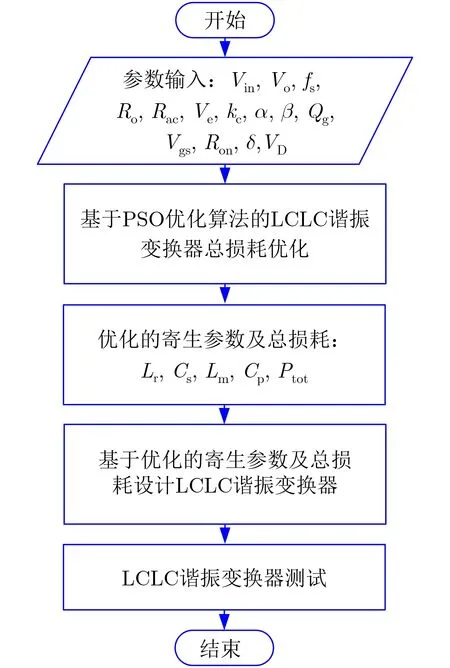
圖2 基于粒子群優化算法的LCLC諧振變換器優化設計

步驟 1 在LCLC變換器優化設計開始之前，根據LCLC諧振變換器的輸入電壓、輸出電壓、工作頻率，確定主開關管、整流二極管型號，并選定磁芯形狀和材料。并根據主開關管的參數、整流二極管參數、磁芯的參數，代入變換器總損耗公式中。

步驟 2 采用粒子群優化設計算法，對LCLC諧振變換器的總損耗進行優化，計算得到優化的諧振參數以及優化的總損耗。粒子群優化算法將在3.2節中詳細闡述。

步驟 3 基于步驟2中的優化的寄生參數，搭建LCLC諧振變換器。

步驟 4 對LCLC諧振變換器進行測試。

3.2 用于LCLC諧振變換器優化設計的粒子群優化設計算法

用于LCLC諧振變換器優化設計的粒子群優化設計算法流程圖如圖3所示，包含以下幾步：

步驟 1 粒子群優化算法初始化。粒子群優化算法的參數，包含Weight.start， Weight.end，kind和Vel.max被初始化。其中，粒子的個數Npa為20，最大的迭代次數Max.Iteration是100。

每一個粒子被賦予任意的Lr， Cs， Lm和Cp值。LCLC諧振變換器的參數輸入到粒子群優化設計算法中，變換器總損耗作為粒子群優化算法的目標函數。

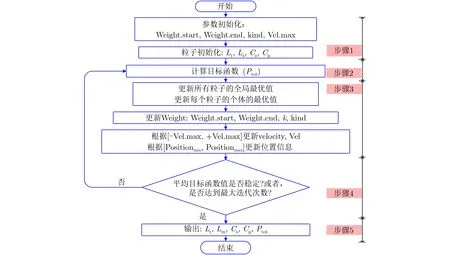
圖3 用于LCLC諧振變換器優化設計的粒子群優化設計算法

步驟 2 總損耗計算。在這步中，計算每個粒子的目標函數值及變換器總損耗。目標函數值將用于評價每個粒子的適應度。

步驟 3 更新全局最優值、個體最優值、Weight和Vel。基于步驟2中計算的總損耗，所有粒子的全局最優值，每個粒子的個體最優值，Weight和Vel將被更新。

步驟 4 重復步驟2和步驟3，直到滿足循環結束條件。如果平均目標函數值穩定，或者達到最大迭代次數，循環過程將被終止。否則，將重復步驟2和步驟3的過程。

步驟 5 輸出優化的諧振參數值以及優化的總損耗。當步驟2和步驟3的循環終止條件滿足之后，粒子群優化算法將輸出優化的諧振參數值以及總損耗。

至此，粒子群優化算法結束。當粒子群優化算法結束之后，將得到優化的諧振參數，包含Lr， Cs，Lm和Cp。接下來，將利用優化的諧振參數，搭建LCLC諧振變換器，并進行實驗測試。

3.3 粒子群優化算法驗證

在3.1節和3.2節中，分別針對基于粒子群算法的LCLC諧振變換器優化設計方法以及粒子群優化算法進行了闡述。本節將采用基于粒子群算法的LCLC諧振變換器優化設計方法，進行LCLC諧振變換器的優化設計，以此驗證本文提出的優化設計方法。

LCLC諧振變換器的參數如表1所示。輸入電壓為40 V，輸出電壓為4800 V，開關頻率為300 kHz，輸出功率為300 W。基于LCLC諧振變換器的輸入、輸出電壓以及開關頻率，磁芯選擇TDK公司的FEE38/16/25，磁芯材料為N87，適于工作在500 kHz以下的開關頻率。此外，主開關管選擇RJK6505PBF。

表1 LCLC諧振變換器參數

基于表1的參數，采用本文提出的基于粒子群算法的LCLC諧振變換器優化設計方法，對LCLC諧振變換器的總損耗進行了優化設計。LCLC諧振變換器的總損耗，隨迭代次數的變化如圖4所示。

由圖4可以看出，隨著迭代次數的增加，變換器總損耗逐漸穩定，最終優化得到的總損耗為8.9 W，對應的諧振參數為Lr= 0.09 μH， Cs=1 μF， Lm= 8.0 μH， Cp= 13.2 nF。當LCLC諧振變換器的優化過程完成之后，第4節將基于優化結果，搭建LCLC諧振變換器并進行實驗測試。

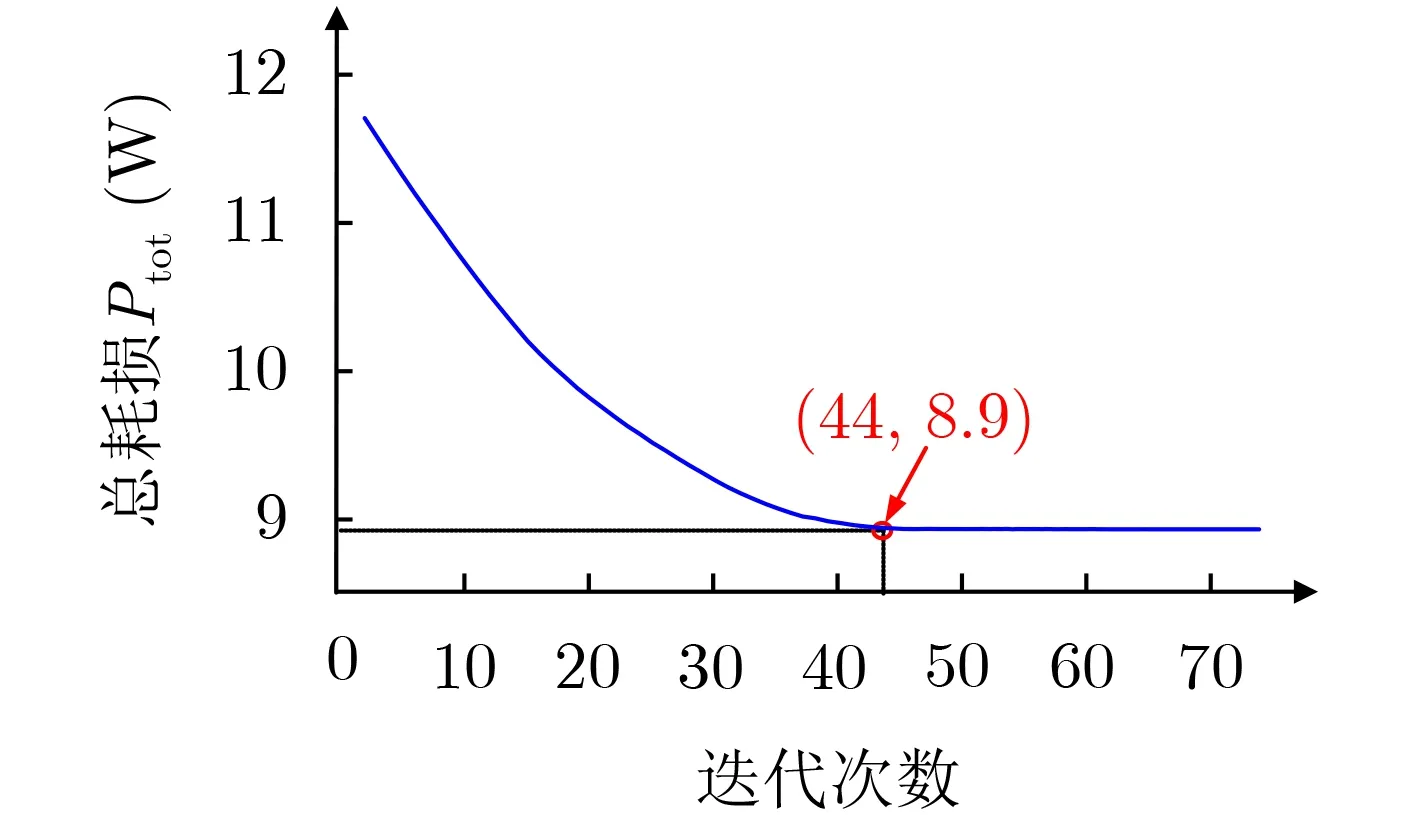
圖4 總損耗隨迭代次數的變化

4 實驗驗證

在本節中，首先，基于第3節的優化設計結果，搭建了優化的LCLC諧振變換器；其次，在優化的LCLC諧振變換器搭建完成之后，進行了一系列實驗，驗證了本文提出的優化設計方法的有效性；最后，在改變輸入電壓和輸出功率的情況下，測試了LCLC諧振變換器的效率。

4.1 LCLC諧振變換器

基于第3節優化設計得到的諧振參數，搭建了LCLC諧振變換器。由于改進用于高壓平面變壓器的部分交錯繞組結構具有低漏感、低寄生電容以及低交流電阻的優勢，本文的高壓變壓器采用了這種結構[15]。改進的用于高壓變壓器的部分交錯繞組結構如圖5所示。

變壓器以及繞組的尺寸如表2所示。

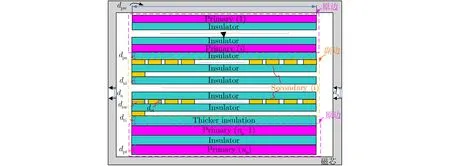
圖5 改進的用于高壓平面變壓器的部分交錯繞組結構

根據表2所示的尺寸，在Ansys Maxwell中搭建了高壓變壓器模型，并進行了有限元仿真。仿真得到的漏感、勵磁電感以及寄生電容如表3所示。

表2 高壓平面變壓器參數

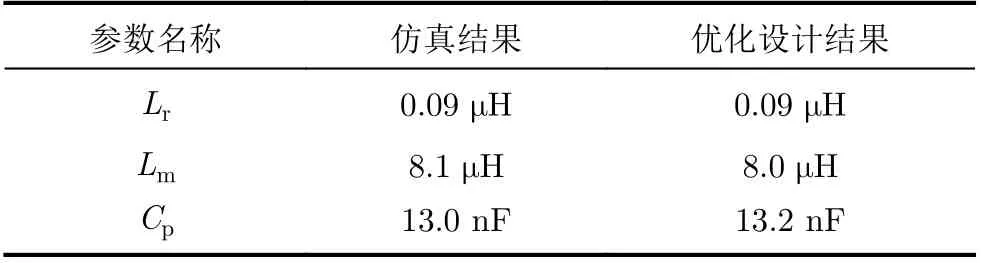
表3 仿真結果與優化結果的對比

由表3可以看出，與優化的諧振參數相比，仿真結果的誤差可以接受。因此，LCLC諧振變換器的優化設計結果得以實現。需要指出的是，由于Cs為分立器件，優化的串聯諧振的電容Cs值，可以直接通過選擇分立電容實現。

4.2 基于粒子群算法的LCLC諧振變換器優化設計方法驗證

LCLC諧振變換器的測試波形如圖6所示。其中，vds1(t)為開關管S1的漏源極電壓，ir(t)為諧振電流，vgs1(t)為主開關管S1的驅動電壓，vd1(t)為倍壓整流二極管D1的電壓，id1(t)為倍壓整流二極管D1的電流。

主開關管S1的實驗波形如圖6(a)所示。由圖6(a)可以看出，在主開關管開通時，諧振電流ir(t)為零，同時，開關管S1上的電壓vds1(t)也為零，因此，主開關管實現了零電壓、零電流開通。同理，當主開關管關斷時，諧振電流ir(t)為零，同時，開關管S1上的電壓vds1(t)也為零，因此，主開關管實現了零電壓、零電流關斷。綜合上述討論，主開關管S1實現了零電壓、零電流開通和關斷。

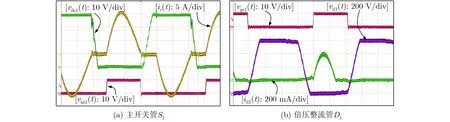
圖6 優化的LCLC諧振變換器的實驗波形

倍壓整流二極管D1的實驗波形如圖6(b)所示。由圖6(b)可以看出，在倍壓整流二極管D1開通時，諧振電流id1(t)為零，同時，倍壓整流二極管D1上的電壓vd1(t)也為零，因此，倍壓整流二極管D1實現了零電壓、零電流開通。同理，當倍壓整流二極管D1關斷時，諧振電流id1(t)為零，同時，倍壓整流二極管D1上的電壓vd1(t)也為零，因此，倍壓整流二極管D1實現了零電壓、零電流關斷。綜合上述討論，倍壓整流二極管D1實現了零電壓、零電流開通和關斷。

基于上述實驗結果可以看出，主開關管和倍壓整流二極管都實現了零電壓、零電流開通和關斷。

為進一步測試本文提出的優化設計方法的有效性，分別測試了當勵磁電感Lm和串聯諧振電容Cs改變時的波形效率。

改變勵磁電感得到的實驗波形如圖7所示。如圖7(a)和圖7(b)對應的勵磁電感分別為29.3 μH以及4.0 μH。測試得到的效率如圖7(c)所示。

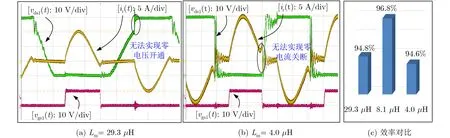
圖7 改變勵磁電感時的測試波形

由圖7可以看出，當勵磁電感Lm偏離優化值之后，LCLC諧振變換器的零電壓、零電流開通和關斷特性將消失：當勵磁電感大于優化值時，主開關管無法實現零電壓開通，此時將引起開通損耗；當勵磁電感值小于優化值時，主開關管將無法實現零電流關斷，此時將引起關斷損耗。由效率對比的結果可以看到，在勵磁電感的優化點，LCLC諧振變換器的效率最高，從而證實了本文所提的優化設計方法的有效性。

改變串聯諧振電容得到的實驗波形如圖8所示。如圖8(a)和圖8(b)對應的串聯諧振電容分別為0.3 μF和1.6 μF。測試得到的效率如圖8(c)所示。

由圖8可以看出，當串聯諧振電容Cs偏離優化值之后，LCLC諧振變換器的零電壓、零電流開通和關斷特性將消失：當串聯諧振電容Cs小于優化值時，主開關管無法實現零電壓開通，此時將引起開通損耗；當串聯諧振電容Cs大于優化值時，主開關管將無法實現零電流關斷，此時將引起關斷損耗。由效率對比的結果可以看到，在串聯諧振電容的優化點，LCLC諧振變換器的效率最高，從而證實了本文所提的優化設計方法的有效性。

由上述實驗可以看出，采用本文提出的基于粒子群算法的LCLC諧振變換器優化設計算法，主開關管和整流二極管都實現了零電壓、零電流開通和關斷。此外，與非優化的參數相比，優化的LCLC諧振變換器可以實現更高的效率，從而驗證了優化設計方法的有效性。

在空間行波管放大器中，由于輸入電壓和負載在變化，因此，需要進一步研究LCLC諧振變換器在不同輸入電壓和負載時的變換器效率。

圖8 改變勵磁電容時的測試波形

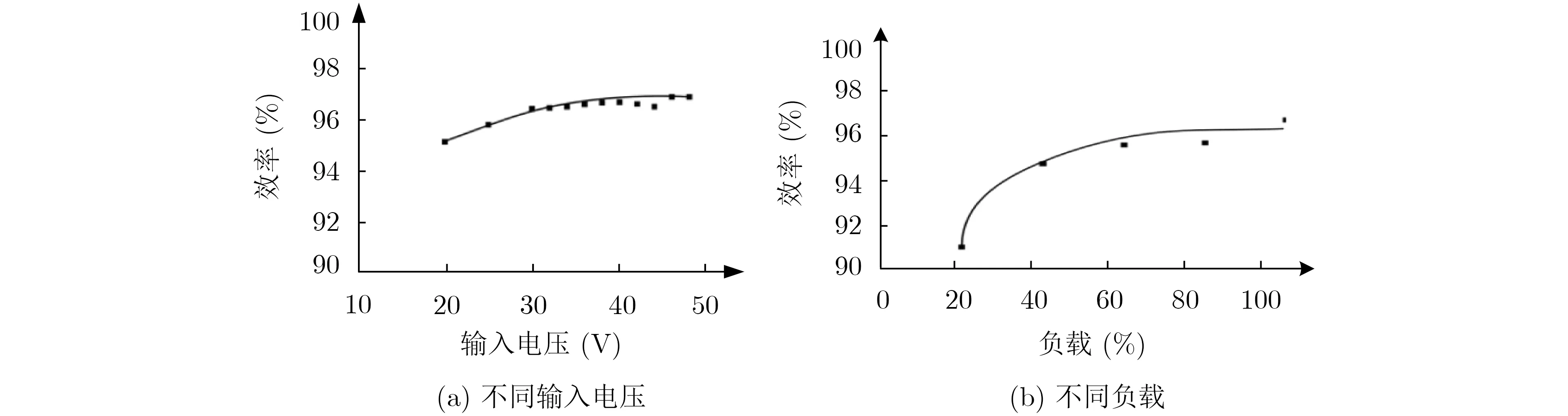
圖9 效率測試

4.3 優化的LCLC諧振變換器在不同輸入電壓和負載時的性能

在空間行波管放大器中，由于輸入電壓和負載在變化，因此，需要進一步研究LCLC諧振變換器在不同輸入電壓和負載時的變換器效率。

優化的LCLC諧振變換器在不同輸入電壓條件下的效率如圖9(a)所示。在額定輸入電壓40 V條件下，變換器總損耗為9.2 W，效率為96.8%。本文提出的優化設計方法計算得到的總損耗為8.9 W，這與實驗測試結果高度一致。變換器效率隨著負載的變化如圖9(b)所示，由圖9(b)可以看出，在寬負載范圍內，LCLC諧振變換器都可以實現高效率。

5 結論

本文提出了一種用于空間行波管放大器的基于粒子群算法的LCLC諧振變換器優化設計方法。這種優化設計方法的目標，是實現LCLC諧振變換器的低損耗、高效率。首先，推導了LCLC諧振變換器的總損耗公式；然后，以該總損耗公式為目標函數，基于粒子群算法進行優化設計，得到了優化的諧振參數以及優化的總損耗；最后，基于優化的諧振參數以及優化的總損耗，搭建優化的LCLC諧振變換器，并進行實驗測試。理論分析以及實驗結果均表明，基于粒子群算法的LCLC諧振變換器優化設計方法，能夠用于LCLC諧振變換器的優化設計，提高變換器效率。