子空間約束的一階秩1干擾下的自適應檢測

鄒 鯤 來 磊 駱艷卜 李 偉

(空軍工程大學信息與導航學院 西安 710077)

1 引言

雷達信號檢測理論是建立在統計假設檢驗基礎上的[1]，檢測性能在很大程度上依賴背景噪聲統計模型。由于在檢測器設計階段，雷達工作環境統計特性無法完全確定下來，因此在對某個待檢測單元進行檢測時，還需要一定數量的參考單元，用于估計待檢測單元背景噪聲統計特性，從而可以自適應調整檢測器中的權值，在抑制噪聲的同時完成信號的檢測，這種檢測方法稱為自適應檢測器。

經典的自適應檢測器，如Kelly[2]提出的廣義似然比(Generalized Likelihood Ratio Test， GLRT)檢測器，采用了單步(1-step， 1S)準則，將待檢測數據和參考數據一起用于構造GLRT檢測器。由于雷達檢測問題一般不存在一致最大勢檢驗，這種GLRT檢測器并不能保證在任何情況下的最優性[3]。因此人們提出了不同設計準則下的自適應檢測器，基于雙步(2-Step， 2S)準則，可以得到自適應匹配濾波器(Adaptive Matched Filter， AMF)[4]，其與基于Wald準則得到的檢測器[5]具有相同的結構，而基于Rao準則得到的自適應檢測器[6]對導向矢量失配較為敏感。

雷達探測環境的復雜性[7]一方面顯著降低了這些經典檢測器的檢測性能[8]，另一方面也促進了自適應檢測技術的發展[9]。假定參考數據協方差矩陣為Rs，而待檢測單元背景噪聲協方差矩陣為Rp。經典的自適應檢測算法要求Rs=Rp，即所謂的均勻性。如果放松這一約束條件，假定Rs=cRp，其中c為某個未知因子，這種探測環境稱為部分均勻場景，對應的GLRT檢測器結構也會發生變化，即所謂的自適應相干估計器[10](Adaptive Coherence Estimator， ACE)。進一步非均勻場景[11]中，即Rs≠Rp，自適應檢測將更加困難。導致場景的非均勻性[12]不僅可以來自探測環境地物分布，也可以來自各種可能的干擾(interference)。干擾對接收信號的影響從統計層面上可以分為1階干擾和2階干擾[13]，其分別影響了回波數據的1階和2階統計特性，其中正交干擾[14]、低秩干擾[15]、子空間干擾[16，17]等都屬于1階干擾。對于噪聲干擾源[18]，也可以看作2階干擾[19]。2階干擾在某些情況下也可以等價于非均勻場景模型[20]。在多通道雷達檢測問題中，噪聲干擾源通常具有明顯的方向性，導致干擾分量具有秩1特性[21]。文獻[22]證明了待檢測單元受到2階秩1干擾時，檢測器結構就是ACE。文獻[23]則考慮待檢測單元和參考數據同時受到1階子空間干擾和2階秩1干擾時的檢測問題。

本文考慮探測環境中存在似噪聲覆蓋脈沖(Noise-like Cover Pulse， NCP)的干擾源，其導致了待檢測單元與部分參考單元受到1階秩1干擾。針對該檢測問題，文獻[24]基于2SGLRT檢驗準則，首先假定噪聲協方差矩陣已知，利用待檢測單元和受干擾的參考數據推導廣義似然比檢測器，然后利用未受污染的參考數據估計噪聲協方差矩陣，將其估計值并代入檢測器中，得到的檢測器為D-NCP-D。由于該檢測器在噪聲協方差矩陣估計時僅僅利用了部分參考數據，導致了在干擾功率較低時，檢測性能較差(檢測概率隨著信噪比的增加不能達到100%，參見文獻[24]圖8—圖10)。本文的主要貢獻在于：

(1) 將1階秩1干擾約束在某個已知的子空間內。子空間約束(Subspace Constrained， SC)表征了干擾分量的先驗信息，充分利用這些先驗信息有助于提升檢測性能。需要指出的是，若該子空間為整個信號空間，對應的檢測問題就退化為文獻[24]的檢測問題，因此D-NCP-D是本文提出的檢測器的一個特例。

(2) 改進檢測器設計準則，提升檢測性能和計算效率。文獻[24]基于2SGLRT檢驗準則中，噪聲協方差矩陣的估計僅僅利用了部分未受干擾的參考數據，由于參考數據使用不充分，檢測性能得不到充分的發揮。本文提出了M2SGLRT和3SGLRT兩種檢測器設計準則，其中基于M2SGLRT準則可以利用全部參考數據用于噪聲協方差矩陣的估計，有效提升檢測性能，而基于3SGLRT準則可以顯著降低檢測器計算量，且檢測性能不劣于D-NCP-D。

2 檢測問題

考慮多通道雷達，天線陣列個數為Na，相干處理間隔內的脈沖數量Np，那么來自待檢測距離單元的回波信號，經過下變頻、正交雙通道數字采樣和匹配濾波之后，可以用一個長度為N=Na×Np的矢量z0表示，假設其服從復高斯分布，協方差矩陣為N維Hermitian正定矩陣M，且假定未知。待檢測單元回波矢量z0中還疊加有未知幅度β0的干擾矢量s，假定該矢量s被約束在由N×r列滿秩矩陣H 的列張成(用＜H ＞表示)的子空間內，即s=β0H φ，其中φ 表示干擾矢量s在＜H＞內的坐標，且未知。本文假定H是已知的，代表了對干擾的部分先驗信息。假定在H1假設下，待檢測單元回波矢量z0中包含了未知幅度α的有用信號v，其也稱為導向矢量。在自適應檢測問題中，還存在K+L個參考數據，即ZL=[z1， z2， ···， zL]， ZK=[z1，z2， ··· ， zK]。這些參考數據也服從復高斯分布，協方差矩陣為M，但參考數據ZL疊加了未知幅度βl的干擾矢量s， l=1， 2， ···， L。綜上所述，考慮如式(1)所示的自適應檢測問題

其中，CN(a，A)表示均值矢量為a，協方差矩陣為A的復高斯分布，符號～表示“服從某種分布”。在這個假設檢驗問題中，未知量包括了有用信號幅度α，干擾分量幅度βl， l=0， 1， ···， L，干擾矢量在子空間內的坐標矢量 φ和背景噪聲的協方差矩陣M。在構造檢測器過程中，如何充分有效處理這些未知參量，將極大影響最終的檢測性能。

2.1 基于2SGLRT的檢測器設計

所謂2SGLRT準則，就是首先假定噪聲協方差矩陣M是已知的，利用待檢測單元數據z0和L個受干擾的參考數據ZL完成GLRT檢測器結構設計，然后再利用K個未受干擾的參考數據完成噪聲協方差矩陣M的估計，將其估計值并代入該檢測器結構中。文獻[24]采用了這種檢測器設計策略，本文進一步假定了干擾約束在某個子空間內，因此文獻[24]獲得的檢測器可以作為本文提出的2SGLRT檢測器的一個特例，即H為單位矩陣的情況。

利用統計假設問題式(1)，在H0下的似然函數可以表示為

其中

將式(4)代入式(3)中得到

在H1下的似然函數可以表示為

其中

如果給定參數β可以得到

采用循環優化的方法可以得到最終估計值，具體方法參見文獻[24]。再將未受干擾的K個參考可以得到噪聲協方差矩陣M的最大似然估計[2]

需要指出的是，如果矩陣H=IN，那么SC-2SGLRT就退化為文獻[24]的D-NCP-D檢測器。從推導過程可以看出，噪聲協方差矩陣M的估計僅僅使用了K個未受干擾的參考數據，如果K取值較小，可能導致噪聲協方差矩陣估計質量變差，嚴重影響了檢測性能。文獻[24]的研究結論中，當噪聲占主導作用時，D-NCP-D檢測器性能明顯下降，甚至當信噪比足夠大時，檢測概率仍然達不到100%。而SC-2SGLRT采用子空間約束干擾模型，可以通過利用干擾的先驗信息提升檢測性能。

2.2 基于M2SGLRT的檢測器設計

采用2SGLRT準則設計檢測器過程中，噪聲協方差矩陣M的估計僅僅利用了K個參考數據，如果K值不夠大，那么必然會帶來M的估計質量降低，影響最終的檢測性能。為此本文提出了一種修正的雙步廣義似然比檢驗(M2SGLRT)準則，其也分為兩個步驟設計檢測器結構。首先假設噪聲協方差矩陣M和干擾矢量在子空間坐標φ已知，利用待檢測單元構造似然比。然后利用L+K個參考數據對噪聲協方差矩陣M和干擾矢量在子空間中的坐標φ進行估計，將估計值代入檢測器結構中，完成檢測器設計。這種設計思路可以充分利用有限的參考數據獲得較好的噪聲協方差矩陣M的估計，對提升檢測器性能是有幫助的。

為此首先給出待檢測單元在H0下的似然函數

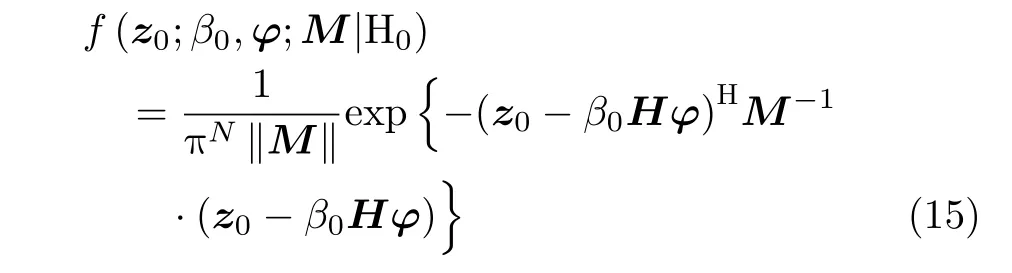
該似然函數中，首先假定僅β0未知，容易得到其最大似然估計

代入式(15)中可以得到

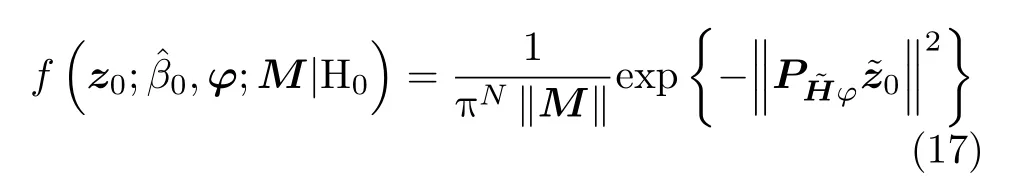
同樣，H1下的待檢測單元似然函數可以寫成

其中，β=[β1， β2， ···， βL]是討厭參數，其不參與最終的檢測器結構設計。可以利用式(11)的方法得到估計值，并代入式(21)中，可以得到

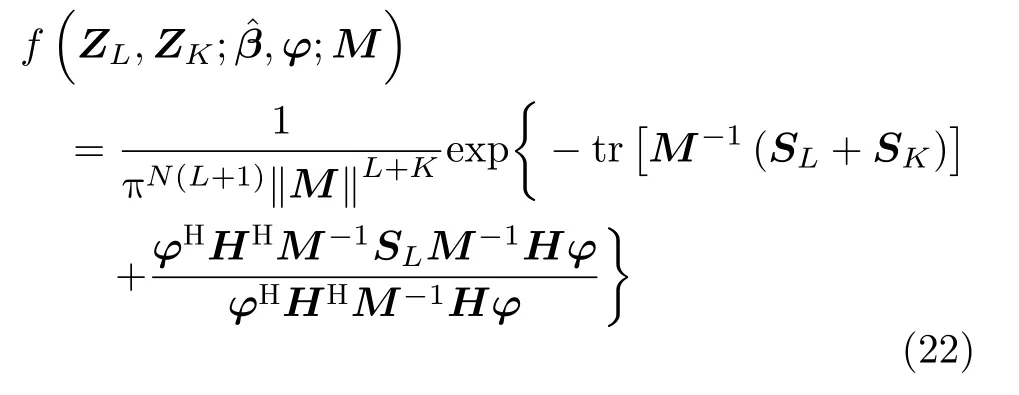
由于參數M和 φ的估計不能單獨給出，為此也可以采用循環優化的方法。當給定M時，利用式(6)的推導方法，可以得到

該檢測器的最大特點在于利用了L+K個參考數據估計噪聲協方差矩陣，從而可以有效提高噪聲占優時的檢測性能。與SC-2SGLRT對比還可以發現，SC-M2SGLRT具有簡單的檢測器結構，其中表示白化后的待檢測數據，和分別是信號和干擾聯合子空間和干擾子空間H～φ上的兩個正交投影矩陣，因此式(25)可以看作在這兩個子空間上投影長度平方差。

2.3 基于3SGLRT的檢測器設計

無論是2SGLRT還是M2SGLRT，得到的檢測器需要用到循環優化方法或不動點迭代算法，這些算法計算量較大。為此本文提出了一種基于3SGLRT的檢測方法，分為3個步驟設計檢測器結構。首先假定噪聲協方差矩陣M和干擾分量在子空間坐標φ已知，利用待檢測單元構造GLRT檢測器，其檢測器結構中包含了未知參數 φ和M。然后假定噪聲協方差矩陣M已知，利用受污染的參考數據獲得干擾分量在子空間坐標 φ的估計值，替換GLRT中的未知參數 φ。最后利用未受干擾的參考數據獲得噪聲協方差矩陣M的估計，并代入GLRT中，替換未知參數M。

該檢測器設計的第1步是利用待檢測單元構造似然比，其推導過程與SC-M2SGLRT相同，可以得到式(20)，噪聲協方差矩陣M的估計為式(13)，參數 φ的為式(23)，將上述估計值代入式(20)中，可以得到最終的檢測器結構

值得指出的是，SC-3SGLRT具有與SC-M2SGLRT相同的檢測器形式，主要區別在于M的估計值不一樣。正是由于此處噪聲協方差矩陣M的估計使用了K個未受干擾的參考數據，因此整個檢測器計算過程中不涉及迭代計算問題，計算效率得到了顯著提升。

3 檢測性能分析

本文采用蒙特卡羅仿真分析檢測性能，基于Neyman-Pearson準則，計算指定虛警概率Pfa的檢測門限，再計算給定信噪比條件下的檢測概率Pd。門限的計算采用了100/Pfa次獨立仿真獲得，檢測概率的計算則是采用了1000次獨立仿真獲得。在仿真噪聲數據過程中，噪聲包含了白噪聲分量和相關噪聲分量，對應的噪聲協方差矩陣M包含白噪聲協方差矩陣和相關噪聲協方差矩陣兩個部分

干擾與噪聲的功率比(Interference to Noise Ratio，INR)則定義[23]為

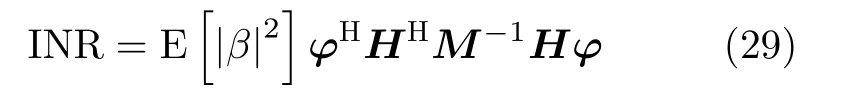
秩1干擾約束在已知子空間內，子空間由矩陣H的列矢量張成。

對于基于2SGLRT和M2SGLRT檢驗準則的檢測器，涉及了迭代計算問題，為此首先分析本文提出的檢測器計算效率問題。M2SGLRT檢測器中在計算噪聲協方差矩陣M的估計時，采用了不動點估計方法，圖1(a)給出了迭代計算過程中兩次計算值之差的范數隨著迭代的變化關系。誤差的計算采用獨立運行10次進行平均。由此可以得到迭代次數與平均誤差的曲線關系。仿真中N取4， 8和16時的不動點估計性能，其中L=N+2， K=N+4。可以看出幾乎只需迭代1次就可以達到最小誤差值，且最小誤差隨N的增加變化不大。圖1(b)給出了3種檢測方法的計算耗時對比分析。這里設定H=IN，因此檢測問題中干擾不受子空間約束，那么2SGLRT檢測器等價于文獻[24]的D-NCP-D檢測器。計算耗時與檢測問題的尺寸N有關，采用200次獨立運行，獲得計算1個統計量所需的時間的平均值，計算機采用的是Intel Core i5處理器。可以看出，隨著N的增加，檢測器計算時間都會增加，但D-NCP-D的運算量最大，而3SGLRT的計算不涉及迭代計算，其計算量最小，M2SGLRT計算量居于上述兩者之間。因此，從本文的分析結果來看，采用M2SGLRT和3SGLRT準則得到的檢測器，具有較好的計算效率。

圖1 數值計算性能分析

再分析檢測性能。在計算機仿真參數中，設定N=8， L=10， K=12，虛警概率Pfa=10—3， H為N×2列滿秩矩陣時，表示干擾受子空間約束，檢測器名稱前帶有前綴符號“SC-”。若H為N×N單位矩陣，表示干擾不受子空間約束，此時檢測器名稱不帶前綴符號。

考慮到INR與檢測性能密切相關，首先分析INR較小時，各種檢測器的性能對比。檢測性能結果如圖2所示。其中圖2(a)為無干擾情況下的檢測性能，圖2(b)為INR=0 dB的檢測性能。可以看出，當干擾功率較小時，采用2SGLRT的檢測器D-NCP-D的性能最差，這是因為其僅僅利用了部分參考數據完成噪聲協方差矩陣的估計，噪聲的抑制能力減弱，最終降低了檢測性能。還可以發現，隨著信噪比的增加，D-NCP-D的檢測概率很難達到100%，這一點與文獻[24]描述是一致的。而采用了子空間約束的SC-2SGLRT檢測器，其檢測性能得到了提升，這說明可以利用干擾的先驗信息提升D-NCP-D的檢測性能。但從仿真結果來看，利用干擾的先驗信息提升檢測性能對3SGLRT的提升效果不明顯，而對2SGLRT和M2SGLRT提升顯著。

當干擾強度較高時，檢測性能如圖3所示。可以看出，隨著干擾強度的增加，D-NCP-D的檢測性能得到了增強，但由于未使用干擾的先驗信息，其檢測性能弱于對應的子空間約束版本SC-2SGLRT。由于干擾功率較強，意味著回波中蘊含干擾的信息較多，因此采用子空間約束對于性能的提升效果減弱了，即SC-M2SGLRT的性能較為接近M2SGLRT，而SC-3SGLRT的性能幾乎與3SGLRT一樣。仔細對比圖3(a)和圖3(b)還可以看出，對于強度較高的干擾，如INR=20 dB， 2SGLRT檢測性能會略高于3SGLRT，但自始至終2SGLRT檢測性能明顯優于其他檢測器性能。因此從仿真分析結果來看，對于高強度干擾，采用子空間約束提升檢測性能效果較弱，但采用合適的檢驗準則可以顯著提升檢測性能。

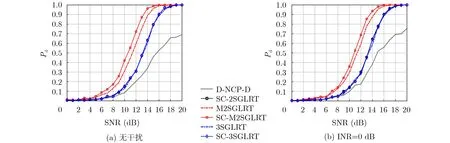
圖2 INR較低時的檢測性能對比分析

圖3 INR較高時的檢測性能對比分析

4 結論

本文針對待檢測單元和部分參考數據受到1階秩1干擾的自適應檢測問題展開研究，提出了干擾受子空間約束時的3種檢測方法。通過理論分析和計算機仿真，得到了如下結論：

(1) 采用子空間約束的秩1干擾模型，由于利用了干擾的部分先驗信息，有助于提升干擾條件下的檢測性能，特別是在INR較低的情況下，采用子空間約束版本的檢測器性能提升明顯。

(2) 采用M2SGLRT準則得到的檢測器，可以獲得較好的檢測性能，其計算量低于2SGLRT檢測器。

(3) 采用3SGLRT準則得到的檢測器，可以獲得較高的計算效率，且僅僅在高INR值時，其檢測性能略低于2SGLRT檢測器。

綜上所述，在干擾功率較強時，推薦采用不受子空間約束的M2SGLRT檢測器，而在干擾較弱時，推薦使用子空間約束版本。對計算效率要求較高時，推薦使用3SGLRT檢測器。2SGLRT計算效率低，且在低INR時的檢測性能下降顯著，一般不推薦使用。