超音速氣流作用下壁板的穩定性分析
李偉杰
(沈陽航空航天大學 航空宇航學院,遼寧 沈陽110136)
壁板是各類飛行器上重要的結構單元,壁板系統的穩定性對于飛行器安全極為重要。氣流速度、支撐方式、材料屬性等都會影響壁板振動特性。國內楊智春等人對壁板的穩定性進行了研究,分析了壁板發生屈曲、顫振、混沌運動、空間混沌等特性的條件[1-4]。研究超音速氣流作用下壁板的穩定性有助于找到設計參數對穩定性的影響,對飛行器設計起到一定的指導作用。本文依據超音速氣流作用下壁板橫向振動微分方程為基礎,利用分岔理論分析了壁板穩定性問題,并分別對各穩定點進行了詳細討論,最后利用數值模擬進驗證了理論的正確性。
1 控制方程
利用活塞理論、Von Karman 大變形理論、Hamilton 原理對超音速氣流作用下的壁板進行力學建模,經推導可得壁板系統的的橫向運動微分方程為:
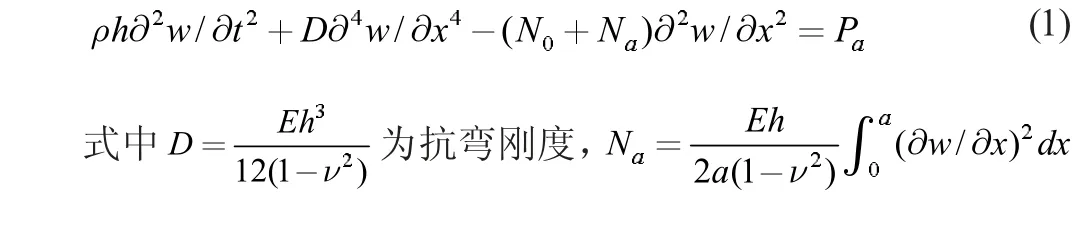
為幾何非線性效應引起的附加面內力,Pa為氣動力。
應用Galerkin 方法進行兩階離散化得到:
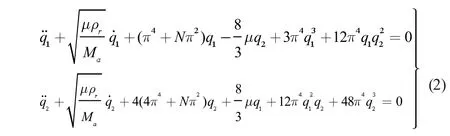
式中,N 為內力系數,μ 為動壓系數,參數變化時平衡點穩定性會隨著發生變化,首先取:


則根據羅斯- 霍維茲判據可分析壁板系統的靜態分岔和動態Hopf 分岔情況。
2 靜態分岔
由式(5)和(8)可得,恒有r1>0;當N>-17π2/5,r2>0,r3>0;當N、μ 滿足
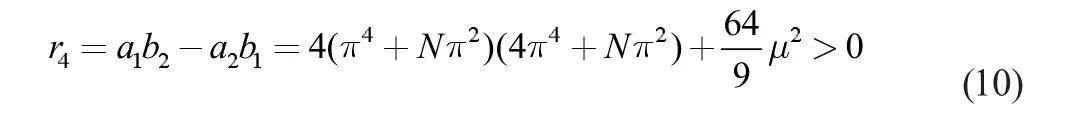
只有一個平衡點Q1。而當不滿足條件(10)時,壁板系統發生靜態分岔,平衡點的個數增加,Q2.3、Q4.5兩者都存在或存在其中之一。由式(6),當:

通過矩陣A 的特征值計算,可以判斷新平衡點Q2.3、Q4.5的類型和穩定性。
3 動態Hopf 分岔
當參數N、μ 滿足下式時,
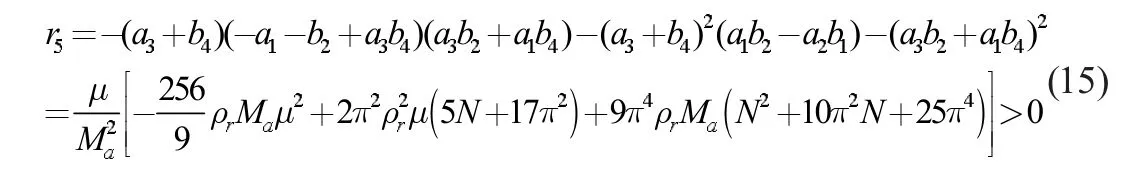
系統只有一個穩定的平衡點Q1;而當不滿足式(15)時,Q1變為不穩定,平衡點沒有增加,系統發生動態Hopf 分岔。
圖1 為壁板系統穩定性區域圖,其中N1=-N/π2。隨著參數穿越各條邊界,平衡點的個數也隨著發生變化,壁板將發生屈曲或顫振。
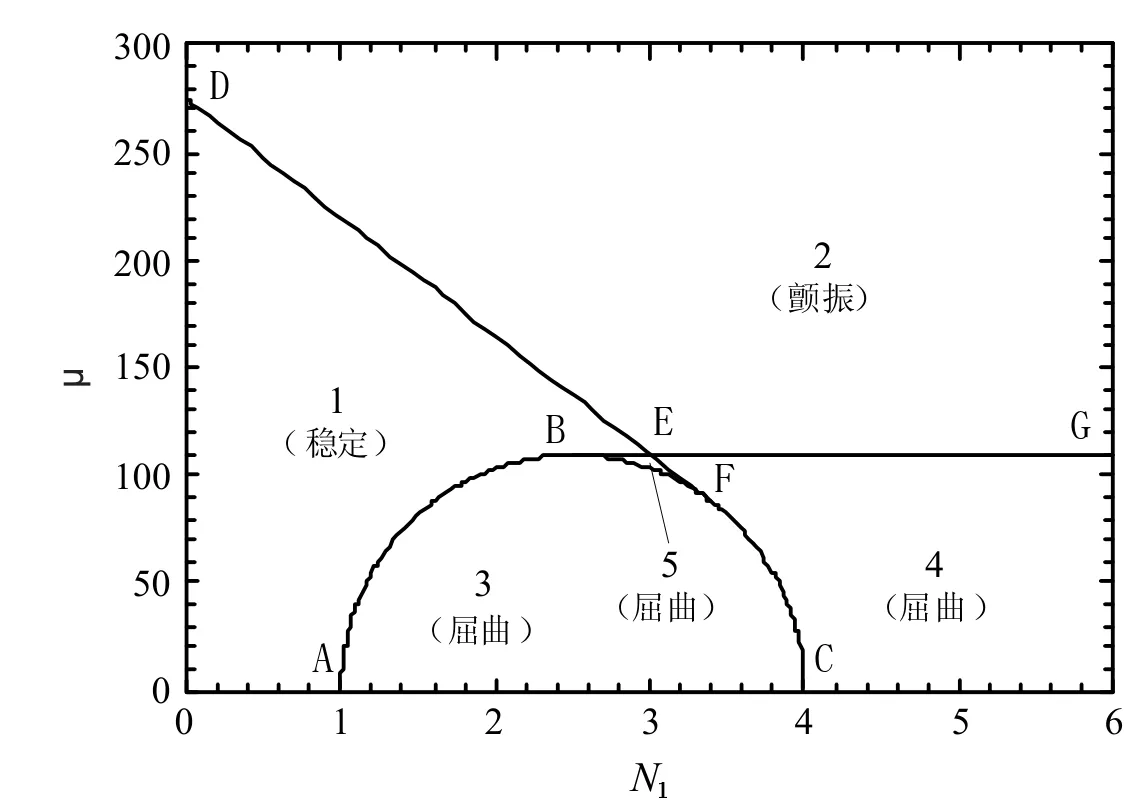
圖1 壁板穩定性區域圖
4 算例分析
取ρr=0.03,Ma=2,利用Runge-Kutta 方法分析平衡點的穩定性和分岔情況,并進行數值模擬。
分別計算了各參數區域內零平衡點的穩定性,表1 給出了Q1平衡點在各參數區域的穩定性分析。
結合圖1 和表1,通過計算分析可得:
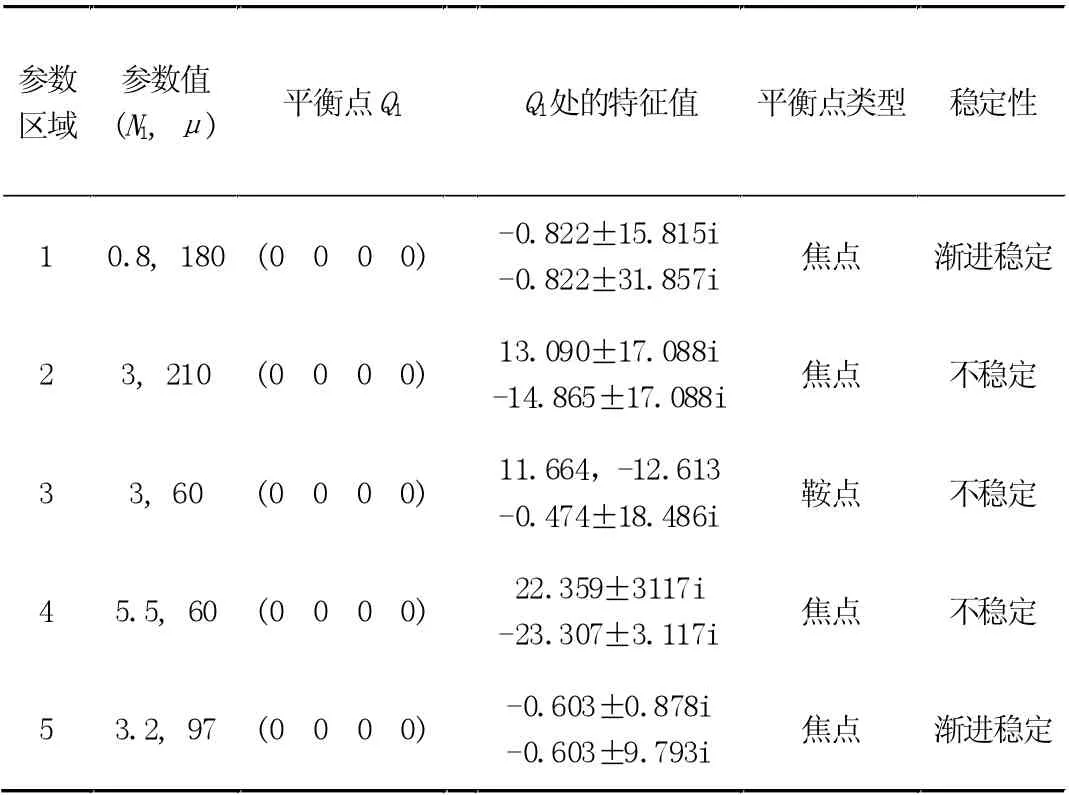
表1 Q1 平衡點在各參數區域內的穩定性分析
在1 區內,系統只有一個穩定的零平衡點Q1,無論初值大小,在相平面圖上相軌跡都趨于平衡點;當參數從1 區進入2 區時仍然只有平衡點Q1,但變為不穩定,發生Hopf 分岔;當參數從1 區進入3 區時,Q1向某一方向失穩,產生了兩個不穩定的新平衡點,壁板發生了屈曲變形;當參數從3 區進入4 區時,Q1又向另外一個方向失穩,新平衡點Q4.5出現,壁板仍然只是發生靜態變形;當參數從3 區進入5 區時,Q1重新穩定,同時還產生兩個新的不穩定平衡點,壁板仍是屈曲變形。
5 結論
在本文中,推導得到了超音速氣流作用下的壁板橫向運動振動微分方程,利用羅斯- 霍維茲判據研究分析了壁板系統的穩定性和分岔問題,得到了系統的穩定性區域圖,發現在某些參數區域內有多個平衡點共存,分別對各平衡點的穩定性進行了分析,并利用數值模擬驗證了理論機理的正確性。

