模糊度量空間中的偽度量結構及等距同構
楊 浩,吳健榮
1.蘇州科技大學 數(shù)學科學學院,江蘇 蘇州 215009;2.南通理工學院,基礎教學學院,江蘇 南通 226002
為描述兩點距離的不確定性,文獻[1]給出了模糊度量(簡稱為KM模糊度量)的概念,文獻[2]對KM模糊度量進行了改進,提出了現(xiàn)在被稱之為GV模糊度量的新概念.文獻[3]對KM模糊度量和GV模糊度量進行了推廣,引入了(L,M)模糊度量的概念.到目前為止,許多經(jīng)典度量空間的重要結果被推廣到了模糊度量空間中[4-10],同時,模糊度量已經(jīng)被廣泛地應用在彩色圖像處理和算法分析中[11-17].為研究模糊度量與分明度量之間的關系,文獻[7]給出了偽度量族空間的概念,建立了兩個分解定理.然而正如文獻[7]中所指出的,這兩個定理成立需要對模糊度量定義中的t-模進行嚴格的限制.
本文引入了星偽度量族的概念,利用這一概念,建立了具有一般t-模的模糊度量的分解定理.此外,在引入模糊度量空間與偽度量族空間等距同構的概念之后,給出了模糊度量空間與偽度量族空間等距同構的充分條件和必要條件.
1 預備知識
本文約定R+=[0,∞),N為自然數(shù)集,?為空集.

(a) *對結合律和交換律成立;
(b) *是連續(xù)的;
(c)a*1=a,?a∈[0,1];
(d) 當a≤c和b≤d時,a*b≤c*d.
則稱*是連續(xù)t-模,常用的連續(xù)t-模包括以下3個算子:?a,b∈[0,1],a*b=a∧b,a*b=max{a+b-1,0},a*b=a·b.
性質1[9]設*是連續(xù)t-模,

(M1) ?t>0,M(x,y,t)>0;
(M2) ?t>0,M(x,y,t)=1當且僅當x=y;
(M3) ?t>0,M(x,y,t)=M(y,x,t);
(M4) ?t,s>0,M(x,y,t)*M(y,z,s)≤M(x,z,t+s);


則稱(M,*)(簡寫成M)是X上的模糊度量,稱(X,M,*)為模糊度量空間.
注1如果將定義2中的(M2),(M5)分別改為:
(M2)′M(x,y,t)=1當且僅當x=y;
(M5)′M(x,y,·)是連續(xù)的.
則(X,M,*)為GV模糊度量空間[2].
若(X,M,*)是模糊度量空間,設x∈X,r∈(0,1),t>0,稱
BM(x,r,t)={y∈X:M(x,y,t)>1-r}
(1)
是以x為心,r為半徑的開球.定理1的證明可參見文獻[2]中相應結論的證明.
定理1設(X,M,*)是模糊度量空間.如果
τM={A?X:?x∈A,存在t>0,0 (2) 本節(jié)引入星偽度量族的概念,并給出模糊度量的星偽度量族分解定理. 定義3設X是一非空集合,*是連續(xù)t-模,{dr:r∈(0,1)}是X×X到R+中的一族映射.若對任意的x,y,z∈X,都有: (SPM1) ?t>0,存在r∈(0,1),使得dr(x,y)≤t; (SPM2) ?r∈(0,1),dr(x,x)=0; (SPM3) ?r∈(0,1),dr(x,y)=dr(y,x); (SPM4) 對固定的x,y∈X,關于r∈(0,1)的函數(shù)dr(x,y)是單調(diào)遞增的; (SPM5) 對任意的α,β∈(0,1),dα*β(x,z)≤dα(x,y)+dβ(y,z); 則稱{dr:r∈(0,1)}是X上的星偽度量族,稱(X,dr:r∈(0,1))為星偽度量族空間. 注2當*=∧時,星偽度量族即為偽度量族.對于一般的連續(xù)t-模*,星偽度量族中的元素未必為偽度量,但為方便起見,我們?nèi)苑Q其為星偽度量族. 為與星偽度量族空間作區(qū)分,我們將由X上的一族偽度量{dr:r∈(0,1)}構成的空間(X,dr:r∈(0,1))稱為偽度量族空間. 定理2設X是一非空集合,D={dr:r∈(0,1)}是X上的星偽度量族,對任意的x∈X,n∈N,r1,r2,…,rn∈(0,1)和ε>0, Vx(r1,r2,…,rn;ε)={y∈X:dri(x,y)<ε,i=1,2,…,n} 則X存在唯一的拓撲τD,使得對任意的x∈X, Vx={Vx(r1,r2,…,rn;ε):n∈N,r1,r2,…,rn∈(0,1),ε>0} 恰好是x關于τD的鄰域基,且τD為X上的Hausdorff拓撲. 證前半部分的證明是常規(guī)的,這里僅給出τD是Hausdorff拓撲的證明. 事實上,對任意的不同的點x,y∈X,由條件(SPM6),存在r∈(0,1),使得dr(x,y)=ε>0.由性質1,存在s∈(r,1),使得s*s>r,從而以及利用條件(SPM4)和(SPM5)可驗證因此τD是Hausdorff的. 引理1設(X,M,*)為模糊度量空間,x,y∈X,r∈(0,1).則: 定理3設(X,M,*)為模糊度量空間,x,y∈X,r∈(0,1).令 dr(x,y)=inf{t>0:M(x,y,t)≥r} (3) 則DM={dr:r∈(0,1)}是星偽度量族. 證只要證DM滿足條件(SPM1)-(SPM6)即可.(SPM2)和(SPM3)是顯然的. (SPM1):?x,y∈X,t>0,由M(x,y,t)>0,則存在r0∈(0,1)使得M(x,y,t)>r0>0.由(3)式得dr0(x,y)≤t. (SPM4):任取r1,r2∈(0,1),r1>r2.因為M(x,y,·)是單調(diào)增的,所以 {t>0:M(x,y,t)≥r1}?{t>0:M(x,y,t)≥r2} 所以dr1(x,y)≥dr2(x,y).因此dr(x,y)關于r∈(0,1)是單調(diào)增的. (SPM6):?x,y∈X,x≠y,由定義2,存在t0>0使得M(x,y,t0)<1.取r0∈(0,1)滿足M(x,y,t0) dr(x,y)=sup{t>0:M(x,y,t) 注3稱上述D={dr:r∈(0,1)}為由模糊度量M導出的星偽度量族. 定理4設D={dr:r∈(0,1)}為X上的星偽度量族,對x,y∈X,t>0,設 MD(x,y,t)=sup{r∈(0,1):dr(x,y) (4) 則(X,MD,*)是一個模糊度量空間. 證以下證明MD滿足條件(M1)-(M6).(M3)顯然成立. (M1):對任意的t>0,取0 (M2):令x=y.由條件(SPM2),對任意的r∈(0,1),t>0,有t>dr(x,y)=0.因此 MD(x,y,t)=sup{r:r∈(0,1)}=1 相反地,假設對任意的t>0,有MD(x,y,t)=1,則對任意的r∈(0,1),MD(x,y,t)>r.由(4)式知,存在1>r′>r,使得dr′(x,y) (M4):任取x,y,z∈X,t,s>0,令MD(x,y,t)=β,MD(y,z,s)=γ.對任意的ε>0且ε dγ-ε(x,y) 因此MD(x,z,t+s)≥γ-ε.由ε的任意性和*算子的連續(xù)性可得 MD(x,z,t+s)≥γ=1*γ≥β*γ=MD(x,y,t)*MD(y,z,s) (M5):對任意的x,y∈X,t0>0和ε>0,有MD(x,y,t0)-ε MD(x,y,t0)-MD(x,y,t)≤MD(x,y,t0)-r0<ε 也就是說MD(x,y,·)在t0處是左連續(xù)的.再由t0的任意性知MD(x,y,·)是左連續(xù)的. 在本節(jié)中,我們將研究模糊度量和偽度量族之間的等距同構關系. (5) 證只需證Φ和Φ的逆映射Φ-1都是連續(xù)的,只要證明: 具體證明過程是常規(guī)的. 推論1設(X,M,*)為模糊度量空間,DM={dr:r∈(0,1)}為由M生成的星偽度量族,則由M誘導的拓撲τM與其對應的由星偽度量族所誘導的拓撲τDM是一致的. 定義5設(X,M,*)和(X′,M′,*′)是兩個模糊度量空間,若存在X到X′上的一一映射ψ,使得?x,y∈X,t>0,都有M(x,y,t)=M(ψ(x),ψ(y),t),則稱ψ是(X,M,*)到(X′,M′,*′)上的等距同構映射,稱模糊度量空間(X,M,*)等距同構于模糊度量空間(X′,M′,*′). (6) (7) 由r的任意性知 (8) 由(7)式和(8)式知 由(6)式知 M(x,y,t)=M′(Φ(x),Φ(y),t) 從而(X,M,*)等距同構于(X′,M′,*′). 推論2設(X,M,*)為模糊度量空間,DM={dr:r∈(0,1)}為由M生成的星偽度量族,MDM為由DM={dr:r∈(0,1)}導出的模糊度量,則(X,M,*)等距同構于(X,MDM,*).因此,由M和MDM導出的拓撲是一致的. 定理7設(X,M,*)為模糊度量空間,若(X,M,*)滿足條件:對任意的x,y,z∈X,s,t>0,有 M(x,y,s+t)≥M(x,z,s)∧M(z,y,t) (9) 證取X=X′,Φ(x)=x(?x∈X).設dr(x,y)由(3)式定義,則由定理3知dr(x,y)為X上的分離的星偽度量族. 于是由(3)式知 再由t1,t2的任意性得 dr(x,y)≤dr(x,z)+dr(z,y) 最后,由dr(x,y)的定義即知(X,M,*)與(X′,dr,r∈(0,1))等距同構. 推論3每個模糊度量(X,M,∧)都可以被分解成X上的一族偽度量. 容易證明,若M(x,y,·)是連續(xù)的,則定理7的逆定理也成立,即: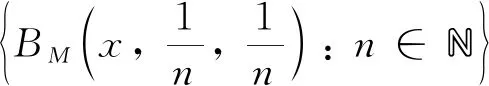
2 星偽度量族





3 模糊度量空間中的等距同構