Delta快速分揀機器人軌跡優化算法研究

章 鴻

(四川信息職業技術學院，四川 廣元 628017)

1 引言

隨著國家2025計劃的實施，工業機器人廣泛應用到各行各業。Delta快速分揀機器手在包裝行業應用廣泛，但隨著其應用在生產中，也出現了諸多問題，尤其在提高搬運效率情況下，抖動特別厲害的問題，因此，如何在保證其生產效率的同時也有保證其穩定性的問題是一個值得研究的科學問題。

關于軌跡規劃和優化問題，文獻[1]對Delta并聯機器人路徑規劃問題進行了研究，給出了一種軌跡規劃的設計思路。文獻[2]針對Delta機器人動態目標抓取問題進行了研究，給出了一種較為準確的抓取方法。文獻[3]對Delta機器人的奇異性分析及空間問題進行了研究，給出了如何避免空間運動中奇異點的方法。文獻[4]利用并聯機器人進行了撿拾禽蛋的研究，但未解決撿拾禽蛋過程因抖動問題引起的禽蛋破裂問題。文獻[5]提出了基于運動學正解的Delta機器人工作空間分析，給出了Delta機器人的運動學模型。文獻[6]提出了Delta并聯機器人極限負載對軌跡控制影響，雖然考慮了負載問題，仍然存在不足。文獻[7]對工業機器人在智能仿形示教系統中抖動問題進行了分析與研究。關于軌跡規劃和優化問題前人做了大量研究，但在實際生產需要中，如何平衡生產效率和穩定性方面值得進一步研究。

以Delta快速分揀機器人軌跡優化為研究對象，提出基于Delta快速分揀機器人抖動和運行時間為優化目標模型，并將遺傳算法應用到模型的優化中，以提高關節空間的動力學性能。最后，通過進行樣機對比實驗驗證了這里所述方法的有效性。

2 工作空間軌跡的設計

根據某企業的快速分揀需求，設計了Delta快速分揀機器人樣機，如圖1所示。在此基礎上確定了快速分揀機器人工作空間的路徑，在工作空間的軌跡規劃中依據快速分揀需求設計了關鍵位置點，如圖2所示。

圖1 Delta快速分揀機器人樣機Fig.1 Delta Rapid Sorting Robot Prototype

圖2 工作空間關鍵點設計Fig.2 Work Space Key Point Design

在Delta快速分揀機器人工作范圍內，基于6個關鍵點，利用三次樣條函數方法對Delta快速分揀機器人的軌跡進行規劃。三次樣條函數表示為下式1[8-9]：

式中：f(x)—工作空間內位移—空間速度—空間加速度，x—每段擬合曲線首尾的時間差。

為了使相鄰x方向和y方向的運動軌跡在位移、速度的相鄰連接位置保持連續可導，建立如式(2)～式(5)所示地合理的工作空間邊界條件。擬合曲線0獨有方程式：

擬合曲線0，1共有方程式：

擬合曲線1獨有方程式：

從圖2工作空間關鍵點設計中能夠發現有x方向和y方向兩個工作空間輸出量，x方向的輸出量包括12，23，34段，利用式(2)～式(5)可得到從關鍵點1到關鍵點4的關于時間的線性方程組，即矩陣Bx=Kx Ax，Bx是15×1的矩陣；Ax為待求系數；且上述矩陣滿足vx1=0，ax1=0，vx4=0，ax4=0。

y方向的輸出量包括01，12段和34，45段，因為34，45段的求解方法同01，12段求解方法相同，故這里只對01，12段進行詳細闡述。01，12段利用式(2)～式(5)求解得到關鍵點0到關鍵點2的關于時間的線性方程組，即矩陣By1=Ky1Ay1，其中，Ky1是12×12的時間矩陣；By1是12×1的矩陣；Ay1為待求系數；且上述矩陣滿足vy0=0，ay0=0，vy2=0，ay2=0。

3 機器人軌跡的優化模型

同時將Delta快速分揀機器人的分揀時間和單次分揀過程中的抖動作為優化對象，并采用權重系數法對時間和抖動進行賦權。依據軌跡規劃的設計要求將Delta快速分揀機器人的運動時間劃分為每一段行程的時間的總和，那么關于時間的Delta2快速分揀機器人優化模型就可以表達為，式中：T—一次分揀工作總時間；hi—第i段軌跡運行時間。Delta2快速分揀機器人在運行過程中的抖動一般由加速度的變化率表示，即。以抖動為目標的Delta2快速分揀機器人的優化模型為。基于上述描述，基于抖動和時間的Delta快速分揀機器人軌跡優化的數學模型表達為：

式中：F—軌跡規劃參量表達；KT—時間權重值；KJ—抖動權重值；N—關節數量；h—每段軌跡時間；—抖動值。

在建立時間-抖動最優軌跡規劃數學模型后，引入遺傳算法[10]，完成模型的優化。群體規模設定為150，交叉概率設定為pc=0.6，變異概率設定為pm=0.17，精英保留策略率設定ps=0.06，編碼因子hi的取值范圍設定為［0.3，4.5］，基因的子空間為[0.3，4.5]，適應度函數表示為：

進而進行選擇、交叉、變異，并對適應度高的個體進行復制，從而提高種群中的整體適應能力，直到收斂準則滿足判斷要求則循環結束。

4 實驗分析

以Delta快速分揀機器人的軌跡規劃及優化為研究對象，進行仿真分析。同時進一步進行實驗驗證，本實驗采用的硬件系統和軟件控制平臺如圖3和圖4所示。硬件系統主要包括兩臺伺服驅動器、一臺工控機以及一些輔助設備組成。軟件控制平臺主要根據Delta快速分揀機器人的操作需求設計一些關鍵功能模塊。

圖3 硬件系統Fig.3 Hardware System

圖4 軟件控制平臺Fig.4 Software Control Platform

為了保證軌跡規劃的有效性，將規劃參數與實際運行軌跡進行對比，其對比結果，如圖5所示。從圖中可以看出，研究方法得到運動軌跡與電機實際運行軌跡相比較雖然實際速度曲線稍有抖動，與指令曲線之間有一定誤差，但已經比較接近。

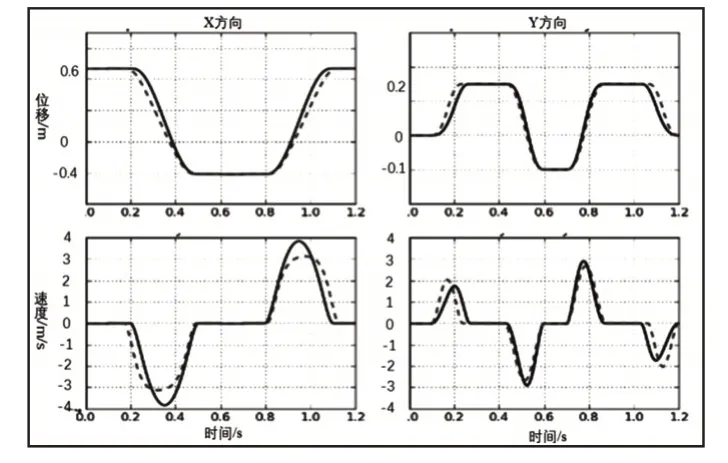
圖5 末端運動規劃軌跡與實際軌跡對比圖Figure 5 Comparison of the End Motion Planning Trajectory with the Actual Trajectory

通過對時間-抖動最優軌跡規劃數學模型進行計算，得到表1所示的優化結果，從表1不難發現，隨著權重的變化，對最終的優化結果有很大影響，說明工作效率和穩定性之間是存在相互影響的，隨著效率越高，其抖動值也越大，穩定性越差。

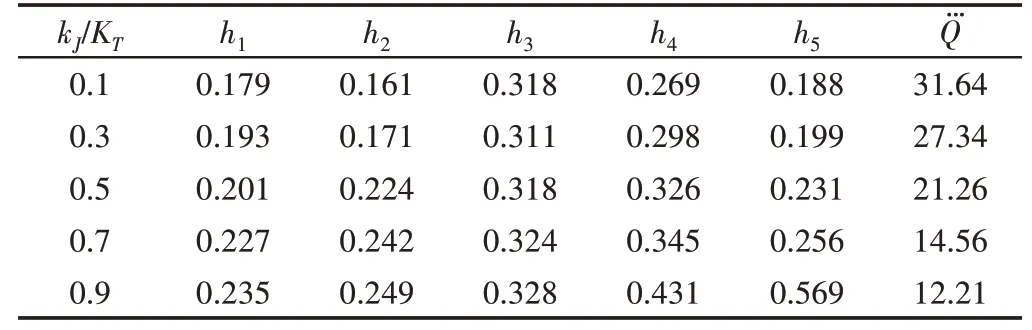
表1 不同權重下運行時間及抖動Tab.1 Run Time and Jitter Under Different Weights

為更進一步分析，分別對上表中各抖動權重值與時間權重值之比分別進行分析。由于不同關節的結果類似，因此僅列出關節1的角加速度以及抖動在不同KJ/KT比值的結果，其中，關節1的角加速度，如圖6所示，抖動關系圖，如圖7所示。從圖6、圖7中不難發現，隨著時間權重設定的越來越大，其角加速度峰值也會隨之越來越大，此時角加速度的平滑度也越來越差，隨之而產的沖擊也會越來越大，其穩定性越來越差；當考慮運行效率和運行平穩性兩個因素時，隨著抖動在兩者之間占有的權重越來越大，抖動程度也呈非線性的減小，關節的運動軌跡越平滑，其穩定性也越來越好。

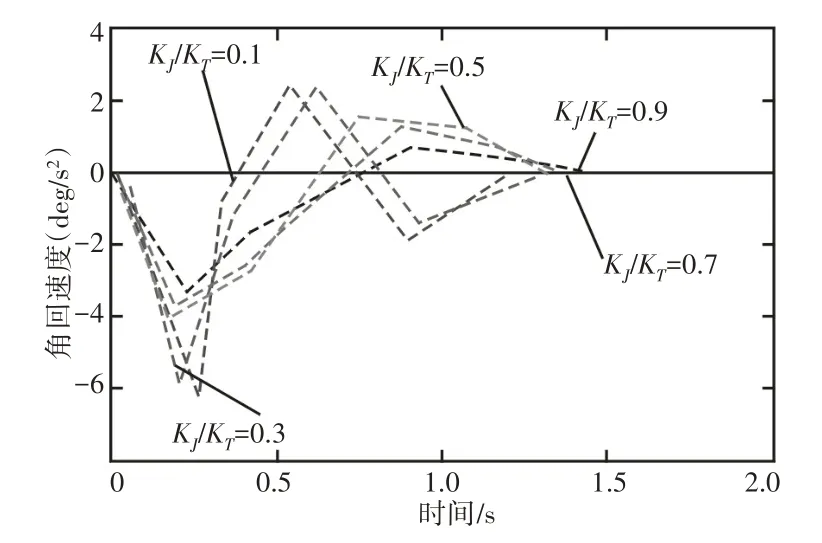
圖6 玻璃搬運機器人關節1軌角加速度曲線Fig.6 The Angular Acceleration Curve of Joint 1 of Glass Handling Robot

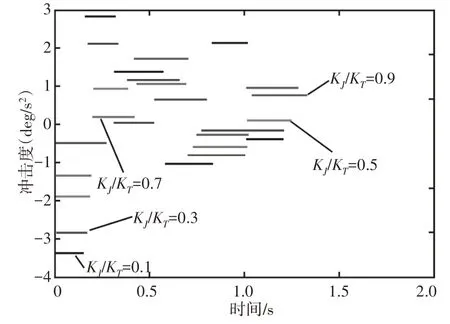
圖7 玻璃搬運機器人關節1抖動函數曲線Fig.7 Glass Handling Robot Joint 1 Jitter Function Curve

5 結論

(1)提出了三次樣條Delta快速分揀機器人空間軌跡的設計方法，并建立了相關的運動學模型，實現了空間軌跡規劃。建立了基于時間-抖動的軌跡優化模型，實現了軌跡的雙目標優化。(2)通過實驗驗證了基于時間-抖動最優軌跡規劃數學模型的有效性，為提高Delta快速分揀機器人的工作空間動力學性能提供參考。