未知時變環境下機器人自校正阻抗控制研究

曾獻文，翟敬梅

(華南理工大學機械與汽車工程學院，廣東 廣州 510000)

1 引言

隨著“中國制造2025”制造強國戰略的不斷推進，機器人已經在工業、服務業領域獲得越來越廣泛的應用，工作任務也不再僅僅需要位置控制，在面對諸多作業場合如人體按摩、皮下注射、柔性體抓取等操作時，需要進行機器人位置和力的雙重控制如阻抗控制。不同于剛性體，上述作業對象具有柔順材料典型的非線性彈性等特征；另一方面，作業對象為非結構化環境，不同作業對象往往具有不同的力學特性，即使同一對象，不同區域的力學特性往往由于生物體征、組織結構等因素而存在變化。上述材料種類及其力學特性的不確定導致阻抗控制力跟蹤誤差較大甚至失去力跟蹤能力。

相關研究表明機器人力、位控制器如阻抗控制器的穩定性及精準性受到環境力學特性的直接影響[1]，因此對環境接觸動力學的研究能夠有效改善機器人阻抗控制器力控制性能。相關工作如李臣[2]在人體按摩機器人柔順控制中采用純剛度模型描述機器人與環境之間的接觸動力學特征。Jones K.C[3]、Koga H[4]基于Kelvin-Voigt模型描述環境動力學對面向人體表面工作的機器人進行力和位置雙重控制。上述研究的接觸動力學模型是線性的，適用于剛性材料的線彈性特征，但對于肌膚之類柔順材料，則無法描述其非線性彈性特征[5]。Hunt–Crossley(HC)模型通過位置和阻尼的耦合同時引入冪指數項，同時表征剛性和柔順材料的力學特征[6]。文獻[7]基于HC模型建立按摩機器人與人體接觸時浸入深度方向上的受力模型，適應肌膚柔性體的非線性彈性等生物力學特征，但是未應用于實際控制系統。

阻抗控制要求建立準確的機械手與環境之間的接觸動力學模型，在未知環境下由于接觸動力學模型參數未知，因此阻抗控制器不能實現穩定力位跟蹤控制效果，需要在經典控制的基礎上進行自適應調整。研究[8]采用自校正控制在未知環境下進行環境參數的在線辨識和控制量的預測調整，但是采用的基于遞推最小二乘辨識算法的自校正控制無法適用于接觸動力學參數存在時變的控制對象。陳雙[9]基于遺忘因子遞推最小二乘法對汽車座椅非線性模型參數進行在線辨識克服了傳統遞推最小二乘算法在面向時變參數時的數據飽和現象。類似地，基于窗函數的最小二乘法[10]在傳統最小二乘算法中引入矩形窗，去除舊數據而只截取一段長度的新數據進行模型參數辨識。但是上述形式的遞推最小二乘法通常難以兼具收斂性和跟蹤性，無法很好地滿足未知時變環境下的參數實時辨識需求。針對上述研究現狀及問題，基于HC接觸動力學模對阻抗控制進行位置規劃，引入自擾動遞推最小二乘辨識算法(SPRLS)至最小方差自校正控制中，實現對未知且時變環境下的接觸動力學模型參數的實時辨識和對阻抗控制參考位置的自適應調整，研究方法可有效跟蹤辨識材料(包括剛性和柔性)的力學特性，并對其進行實時、準確的力位跟蹤控制。

2 基于HC非線性模型的阻抗控制系統

基于位置的阻抗控制中位置誤差x-xd與力誤差Fr-F之間的傳遞函數G(s)：

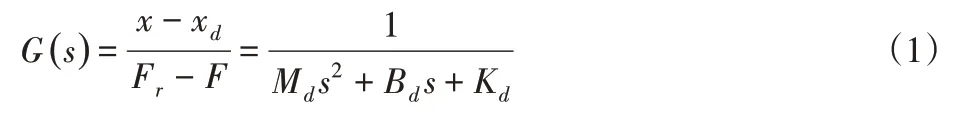
式中：Md、Bd、Kd—期望阻抗模型的慣性矩陣、阻尼矩陣和剛度矩陣，x—機器人末端實際位置，xd—機器人期望的軌跡，在浸入深度方向上，xd—達到期望接觸力所需要的機器人末端運動位置。F—機器人末端與環境的實際接觸力，Fr—期望力。實際控制時，xd不能直接得到，通過接觸動力學模型計算得到期望力對應的位置記為xr，稱為參考位置。

HC接觸動力學模型[6]具有如下形式：

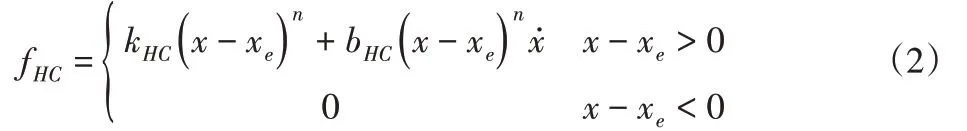
式中：LkHC和bHC—彈性和阻尼系數，n—由接觸體的局部接觸區域中的材料和幾何性質決定的冪指數，n的存在使HC模型更好的描述接觸力隨侵入深度的非線性變化，當指數n=1時則表征了線彈性物體的力學特性。

基于HC模型進行xr的預測輸入，此時機器人末端執行器達到目標位置便不再進給，進給速度x˙=0。此時的接觸力fHC=Fr，機器人末端位置x=xr，xe是環境未受力變形時的初始位置。代入上式(2)得到：

建立面向柔順和剛性材料的阻抗控制系統框架，如圖1所示。

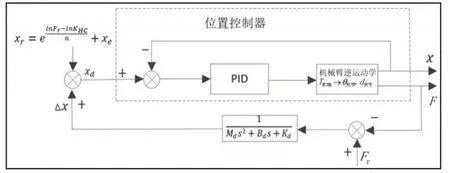
圖1 基于HC模型的阻抗控制系統Fig.1 Impedance Control System Based on HC Model

3 面向未知環境的融合SPRLS算法的自校正阻抗控制系統

基于HC模型的阻抗控制算法中，系統輸入xr的確定，需kHC、n、xe等環境參數，而實際控制中這些參數往往未知；不同作業區域的力學特性存在變化，機器人在不同區域間運動導致接觸動力學參數存在時變；且單純阻抗控制還未考慮信號噪聲、工業延時等干擾因素的影響，以上環境力學特性參數的不確定性和外界干擾將會對傳統阻抗控制的力跟蹤性能產生不利影響。

為適應未知、時變作業對象的動力學特性，提出融合最小方差控制與SPRLS算法的自適應阻抗控制系統，通過前向檢測預測誤差來判斷環境力學特性的變化，并據此設置自擾動項，實現對接觸動力學模型參數的實時跟蹤辨識；同時，基于辨識結果設計最小方差自校正調節器，實現對未知時變環境下阻抗控制參考位置的自適應調整，具體結構，如圖2所示。

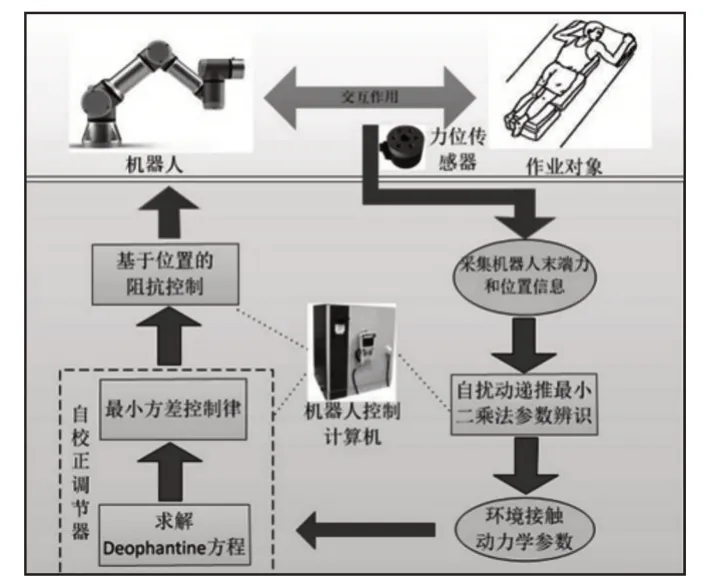
圖2 融合SPRLS算法的自校正阻抗控制系統結構框架Fig.2 Structure of Self-Tunning Impedance Control System with SPRLS Algorithm

3.1 HC模型的自擾動遞推最小二乘參數辨識

自擾動遞推最小二乘法核心思想是在線辨識的過程中檢測前向預測誤差，據此設置自擾動項，在前向預測誤差大于閾值時，介入自擾動項增加參數遞推估計時的迭代量。在前向預測誤差小于閾值時，自擾動項歸零，等效于標準遞推最小二乘算法，不影響收斂性。實現辨識算法對環境參數變化的快速響應以及參數辨識的收斂性，算法流程見圖3模塊1。

普通辨識算法不適用于對于HC模型的非線性結構，目前的解決方案有二階辨識算法[6]和一階辨識算法[11]，相比于二階辨識算法，一階辨識算法將模型轉化為線性化形式，其收斂條件更易于滿足，具有更高的魯棒性。故使用一階辨識算法將HC模型轉換為線性形式，并采用自擾動遞推最小二乘法對其進行單點參數辨識。根據對HC模型下參考位置的推導式(3)整理并經一階辨識算法對等式兩邊取自然對數，化為如下線性形式：

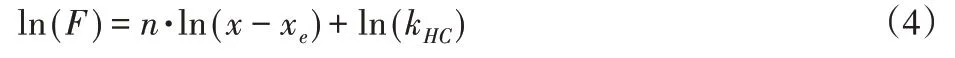
上式(4)寫成最小二乘形式：

其中，Yk=ln(F)

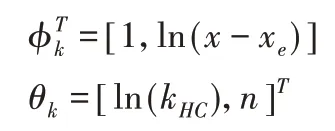
按照自擾動遞推最小二乘法，算法的遞推方程如下：

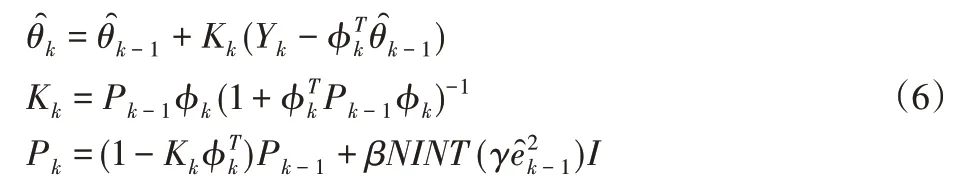
式中：β和γ—擾動增益和誤差增益；I—單位矩陣，NINT()的表達式為：

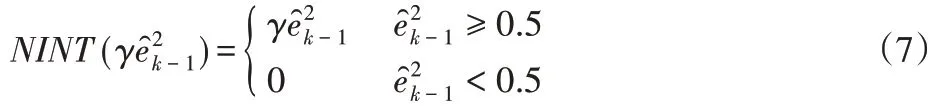
3.2 基于參數辨識結果的最小方差自校正調節器設計

自校正控制系統在獲取模型參數辨識的同時，最小方差自校正調節器按照最小輸出方差為目標進行輸入調整。其基本思想：由于機器人控制存在純延遲d，因此要使輸出方差最小就需要提前d步對輸出量做預測并設計所需控制。對式(4)進行參數辨識后，對應如下形式的時間平移算子多項式：

其中，u=ln(x-xe)；y=ln(F)-ln(kHC)；

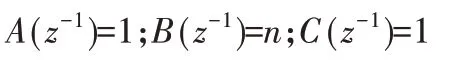
ξ(k)—方差為σ2噪聲，d≥1—控制延時。

基于k時刻的輸入和輸出，對k+d時刻的輸出的預測記作，則預測誤差：。

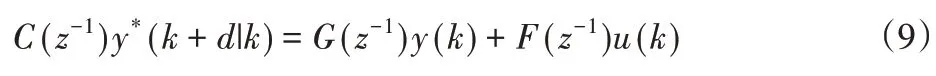
式中E、F、G式滿足如下Deophantine方程：

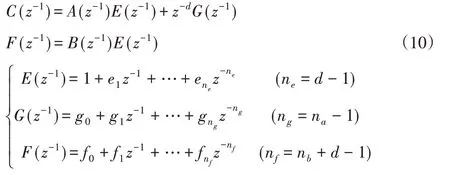
B(z-1)為Hurwitz多項式，設控制目標是使輸出y(k+d)跟蹤期望輸出yr(k+d)要滿足如下性能指標：

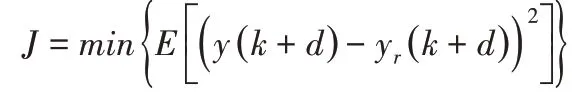
最小方差控制率為：

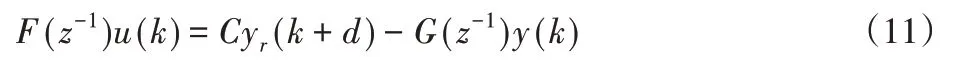
最小方差自校正調節器結構見圖3模塊2。

基于前述自校正控制算法進行阻抗控制參考位置自適應調整，根據對自校正調節器輸入u的最優預測，將u中的機器人末端位置量x作為阻抗控制參考位置輸入圖3模塊3所示的阻抗控制系統實現對阻抗控制的位置修正。具體算法及其相互關系，如圖3所示。

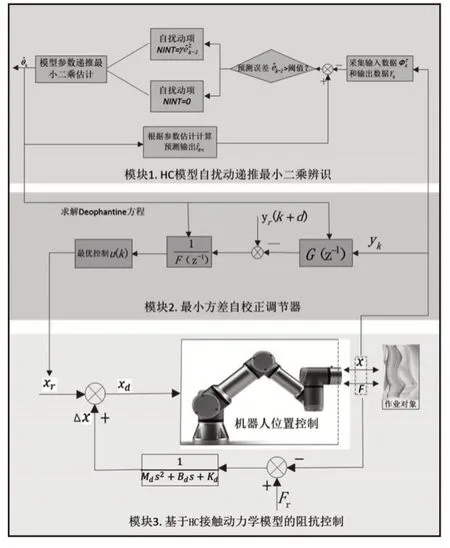
圖3 融合SPRLS算法的自校正阻抗控制系統Fig.3 Self-Tunning Impedance Control System with SPRLS Algorithm

4 仿真實驗及分析

為模擬環境力學特性參數未知且在不同作業區域間存在差異的應用場景，設基于HC模型的環境動力學參數未知且時變，線彈性和非線性彈性兩種環境并存。設環境的真實動力學特性如下：

第(0～100)個采樣周期內：F=1.9(x-6)；

第(101～200)個采樣周期內：F=2(x-7.5)1.2；

第(201～400)個采樣周期內：F=2.5(x-9)1.4。

第(0～150)個采樣周期內期望力Fr=10N，(151～300)個采樣周期內Fr=5N，(301～400)個采樣周期內Fr=10N。

這里設xe在6、7.5、9間變化，可經視覺設備獲取。設機器人延時d=4，外界干擾為方差為0.05的白噪聲；阻抗控制的阻抗參數設為Md=65Bd=15Kd=1。

仿真結果如圖4～圖6及表1、表2所示，k為第k個采樣周期。

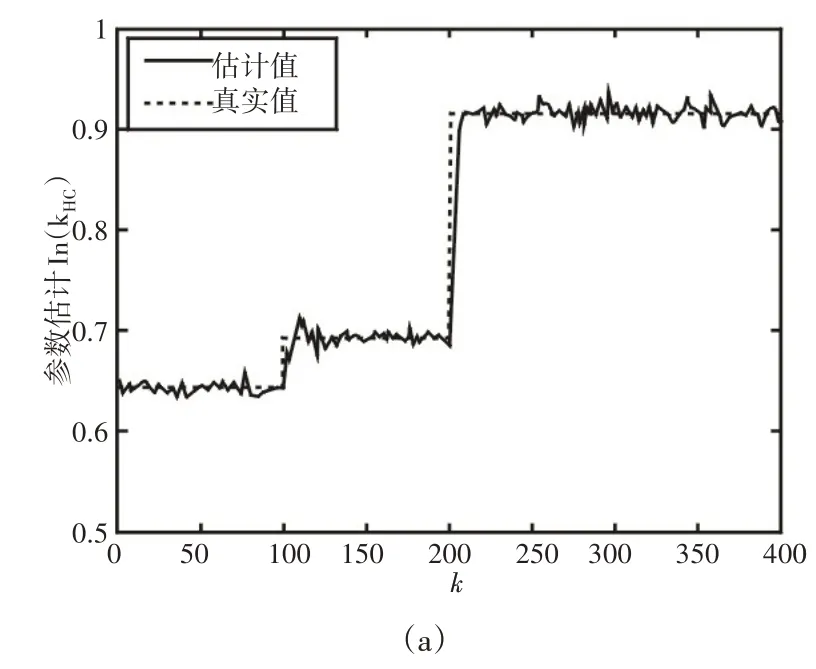
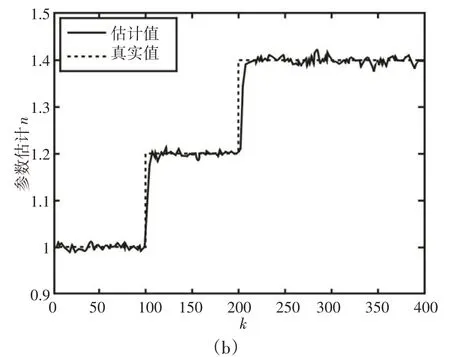
圖4 參數ln(kHC)、n辨識過程Fig.4 Identification Process of Parameter ln(kHC)、n

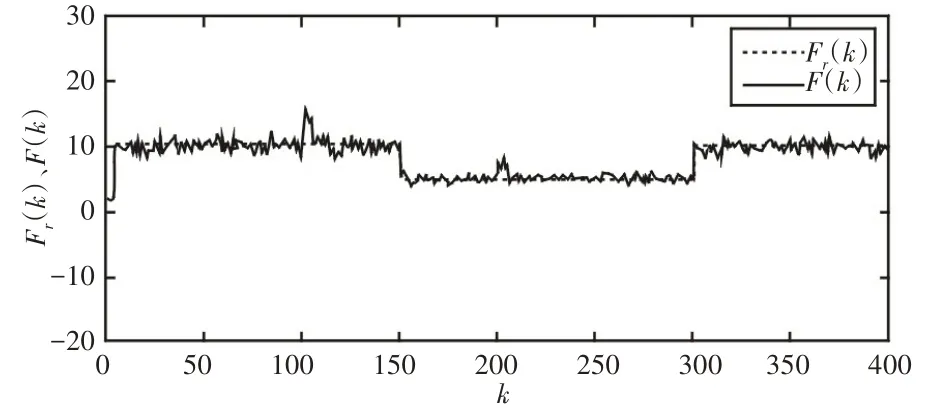
圖5 自適應阻抗控制系統力跟蹤效果Fig.5 Force Tracking Effect of Adaptive Impedance Control System

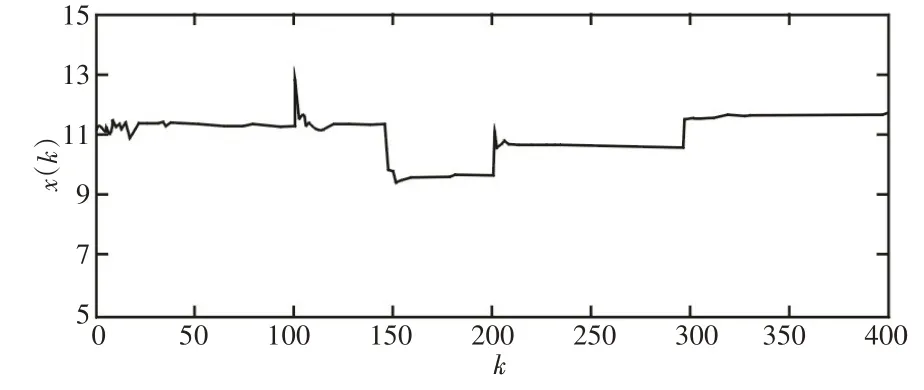
圖6 機器人末端浸入環境方向的位置量Fig.6 Amount of Robot Tip’s Position Immersed in the Environment.

表1 力跟蹤穩態誤差Tab.1 Steady State Error of Force Tracking

表2 環境突變時控制效果Tab.2 Control Effects when the Environment is Changed

在仿真實驗中，環境模型事先未知，且在多個時刻存在參數的突變，期望力也存在變化，實驗結果及分析可見：

(1)由表1和圖5中穩態接觸力可見，接觸力穩態均值與期望值吻合，誤差小于2%，力控制效果穩定良好。

(2)由圖4可見SPRLS算法對時變環境特性參數能夠實現較好的跟蹤辨識，且當環境參數發生變化時，由表2和圖6可見接觸力存在短暫小范圍變化后便穩定到期望值，對于期望力的變化也能實現很好的力跟蹤效果。

(3)由圖6可見在接觸面浸入方向上，機器人末端始終與環境有效接觸并根據力跟蹤需求調整浸入深度。

為了進一步驗證所提出的算法合理性，與當前多種算法進行了對比仿真試驗：基于HC模型分別結合遞推最小二乘(RLS)、窗函數遞推最小二乘(BLS)[10]、遺忘因子遞推最小二乘(FFRLS)辨識方法[9]的最小方差自校正控制(MVSTC)算法。對比實驗結果，如圖7、圖8及表3所示。

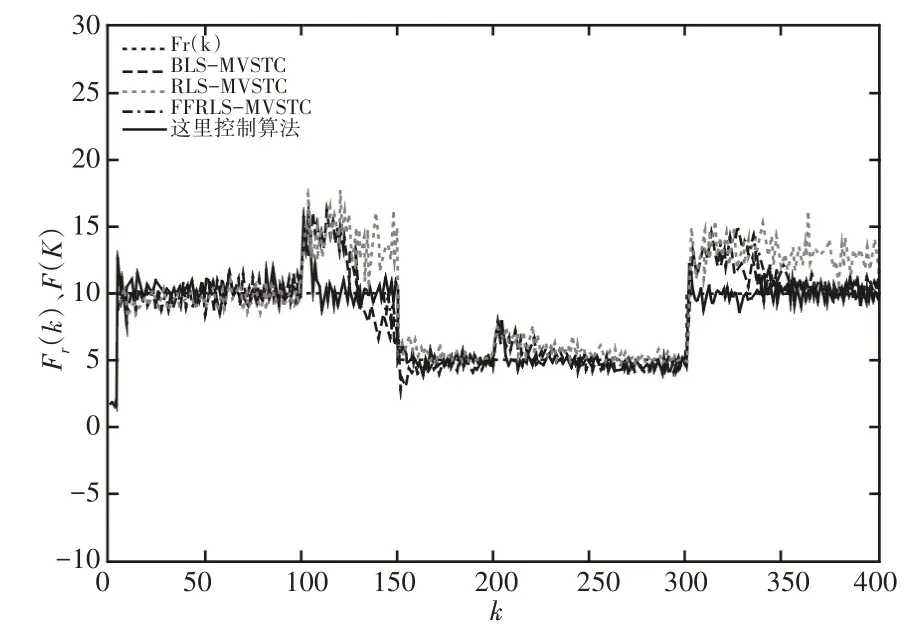
圖7 對比試驗結果Fig.7 Results of Comparitive Experiment

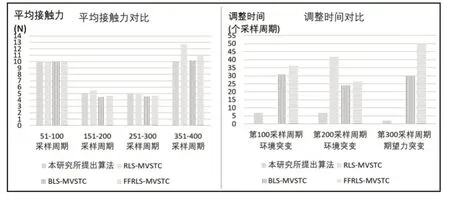
圖8 算法力跟蹤性能對比Fig.8 Comparison of Different Algorithms’Force Tracking Performance

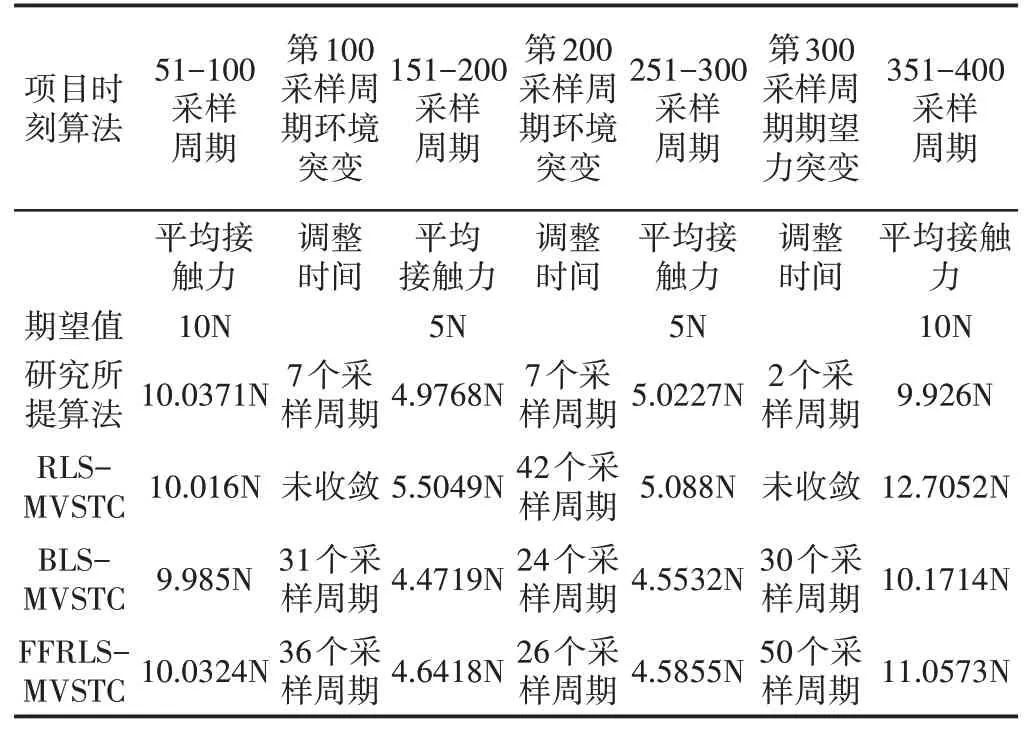
表3 對比實驗力跟蹤數據分析Tab.3 Force Tracking Data Analysis of Comparative Experiments

由圖7、圖8及表3對比試驗結果可知：

對于非線性彈性接觸環境，由于實際跟蹤控制要基于其線性化后的數學對象，因而所提算法及對比實驗在環境力學特性突變時力突變均存在一定誤差擴大，但是在以下方面有較大區別：

(1)傳統基于遞推最小二乘辨識的自校正控制不能適應環境力學特性的變化，環境力學特性出現變化時會產生力跟蹤誤差，最大達期望值的27%，本研究所提算法的穩態接觸力誤差則小于期望值的2%；

(2)期望力發生變化時，本研究所提算法能夠很快調整進給量實現實時跟蹤，其他三種算法則有較大延時。

(3)基于窗函數遞推最小二乘和遺忘因子遞推最小二乘參數辨識的自校正控制，在環境力學特性變化時的跟蹤調整時間較大，本研究所提算法調整時間減少約70%。

可見環境參數存在未知和變化時，基于HC模型，結合自擾動遞推最小二乘辨識的最小方差自校正阻抗控制能夠保持柔順控制能力的基礎上，具有較快的反應速度和收斂能力，控制效果準確穩定。

5 結論

針對當前環境力學特性未知或時變下的力位控制問題，提出了基于HC接觸動力學模型的自校正阻抗控制算法，在多個時變環境下進行仿真實驗與分析，驗證了提出方法的適用性和有效性，該算法具有如下優點：

(1)基于HC接觸動力學模型指導機器人阻抗控制的參考位置規劃，阻抗控制系統對柔順材料和剛性材料都具有較好適用性。

(2)在環境動力學特性未知且存在時變的情況下，提出的結合SPRLS算法的自校正阻抗控制系統，能夠快速穩定地跟蹤辨識接觸動力學參數，并克服機器人控制延時，實時自適應調整阻抗控制參考位置，穩態力跟蹤誤差小于2%，環境特性突變時的控制調整時間僅約7個采樣周期。