基于強化學習的航空器機場智能靜態路徑規劃

疏利生，李桂芳，嵇勝

（南京航空航天大學民航學院，南京210016）

0 引 言

隨著人工智能技術的迅速發展，我國已有上百個地區提出建設“智慧城市”。民用航空機場作為城市交通中的重要組成部分，“智慧機場”概念的提出和發展也逐漸得到行業的認可和推廣。機場地面作為飛機活動的主要區域，研究人工智能在機場地面航空器運行中的應用具有重要意義。

目前研究航空器在機場地面滑行道和跑道上運行問題的建模方法中，多采用整數線性規劃模型、有向圖模型和Petri網模型。2004年，J.W.Smeltink等［1］在研究中指出，航空器場面滑行優化的研究可以通過構建整數線形規劃模型的方法進行研究，提出構建模型的過程中需要考慮場面航空器滑行沖突，以此降低航班延誤；2006年，G.Chang等［2］針對復雜的停機坪調度問題，通過有向圖模型模擬仿真了機坪管制的調度過程，并通過面向對象的技術實現了場面運行仿真；2007年，H.Balakrishnan等［3］構建了優化最短航空器地面滑行時間的整數線形規劃模型，通過調配場面運行沖突點來規劃滑行路徑；2011年，朱新平等［4］運用Petri網構建了航空器場面運行模型，模型中從避免航空器沖突的方向設計了實時控制沖突預測算法，通過仿真分析了模型有效性；2012年，H.Lee等［5］為縮小MILP模型規模，在模型中引入了滾動窗口，通過仿真實現了航空器場面滑行路徑優化和進離場路徑選擇和排序優化；2018年，潘衛軍等［6］構建了基于有色Petri網的航空器滑行路徑優化模型，并通過實例仿真驗證了所構建的路徑優化模型的合理性。綜上所述，國內外針對機場場面航空器滑行路徑建模問題研究較多，也較為深入，但研究基本針對某一條件下的應用，對應用條件和范圍限定較大，缺乏普適性。

強化學習（Reinforcement Learning，簡稱RL）理論最早于20世紀50—60年代提出，經過多年發展，強化學習的理論已經十分成熟。目前強化學習在交通控制、機器人移動和學習分類等領域廣泛應用，但在機場地面航空器路徑規劃中的應用還未有學者對此研究，而“智慧機場”未來的發展離不開更加高效的場面運行環境。

本文提出一種基于強化學習的航空器靜態滑行路徑規劃方法，構建機場地面航空器移動強化學習模型，模型中考慮了機場地面航空器滑行規則；采用Python內置工具包Tkinter編寫海口美蘭機場模擬環境，運用時序差分離線控制算法QLearning求解模型，生成符合機場地面航空器實際運行的滑行路徑。

1 機場地面航空器移動強化學習模型

按照機場真實環境轉化過程，航空器移動到下一個位置與上個位置有關，還與之前的位置有關，這一模型轉換非常復雜。因此本文對強化學習的模擬機場環境轉化模型進行簡化，簡化的方法就是引入狀態轉化的一階馬爾科夫性，也就是智能體（航空器）移動到下一個位置的概率僅和上個位置有關，與之前的位置無關。

1.1 馬爾科夫決策過程

在強化學習的算法中，馬爾科夫決策過程（Markov Decision Process，簡稱MDP）［7］可表示為(S，A，R，P)：S表示狀態集合（State），即機器人可能感知到所有環境狀態的集合；A表示動作集合（Action）；R表示獎勵函數（Reward Function）；P表示動作選擇策略。

智能體集合（Agent）：把在機場場面運行的每一個航班作為MDP的Agent，每個Agent都攜帶位置和獎勵信息。當航班進入滑行道時，Agent進入活動狀態，當航班離開滑行道時，Agent進入無效狀態。Agent的數量是固定的，但是每個時刻t活動的Agent數目隨時間變化，在本文中，主要考慮靜態路徑規劃，故不考慮多駕航空器同時運行的情況。

狀 態 集 合（State）：s∈S，狀 態是Agenti∈{1，…，N}在時刻t∈{1，…，T}的位置。當網格化機場場面時，表示在時刻tAgent所處的網格單元。在時長T范圍內一個Agent占據所有單元格表示該航空器在機場場面的滑行路徑，共設置231個狀態。

動作集合（Action）：a∈A，Agent在時刻t的動作表示為at。以網格系統為例（如圖1所示），Agent可以從向上、向下、向左和向右四個動作中選擇動作，每個動作會使得航空器沿滑行道方向移動到下一個狀態中。

圖1 Action動作示意Fig.1 The example of Action

獎勵函數（Reward Function）：Agent采取某個動作后的即時或者延時獎勵值。對于RL，需要設計適當的獎勵函數以評估Agent在給定狀態下采取某一動作的價值。Agent在時刻t的獎勵（以r t來表示）主要考慮兩個因素，即航班的全部動作滿足時間約束的程度以及航班在滑行過程中是否遭遇障礙。Agent的獎勵函數定義如下：

式（1）中，ξ＞0表示Agent在時刻t到達所需網格單元（或者狀態）s~時獲得的獎勵；φ＞0表示代理移動到不允許的網格單元時受到的負面激勵，如滑行道之外的單元格；每個Agent在時刻t的目標是獲得總預期累計最大的獎勵。

動作選擇策略Pπ(s)→a：航空器Agent根據當前狀態s來選擇即將進行的動作，可表現為a=π(s)或者π(a|s)=Pr(s′|s，a)，即在狀態s下執行某個動作的概率，s′表示下一個環境狀態。

1.2 強化學習模型

強化學習的基本原理：如果Agent的某一個行為策略獲得環境的正面獎勵，Agent以后產生這個行為策略的趨勢便會加強。Agent的目標是在每個離散狀態發現最優策略以使期望的折扣獎勵累計值最大。

結合強化學習構建的航空器智能移動模型，將學習看作試探評價過程。航空器Agent選擇一個動作用于模擬機場環境，模擬機場環境接受該動作后狀態發生變化，同時反饋航空器Agent一個即時或者延時的獎勵或懲罰，航空器Agent根據環境當前反饋選擇下一個動作，選擇的原則是使航空器Agent得到正面獎勵的概率增大。航空器Agent選擇的動作不僅影響即時的獎勵值，還會影響下一個狀態的獎勵值以及最終的獎勵值，即延時獎勵值。強化學習模型框架如圖2所示。

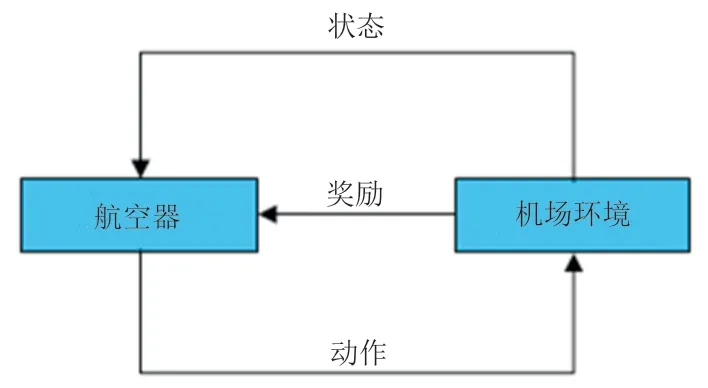
圖2 航空器機場地面移動強化學習模型框架Fig.2 The framework of aircraft airport ground model based on RL

基于累計獎勵，引入貝爾曼最優方程和最優價值函數。

Bellman最優方程［8］：

式中：γ為折扣因子，折扣因子表示對未來獎勵的重視程度［9］；u*(s)為航空器Agent處于s狀態的長期最優化價值，即在s狀態下航空器Agent考慮到所有可能選擇的后續動作，并且都選擇最大價值的動作來執行所帶來的長期狀態價值；q*(s，a)為處于s狀態下選擇并執行某個動作后所帶來的長期最優價值，即在s狀態下航空器Agent選擇并執行某一特定動作后，假設在以后的所有狀態下進行狀態更新時都選擇并執行最大價值動作所帶來的長期動作價值。

最優價值函數［10］為所有最優策略下價值函數的最大值。

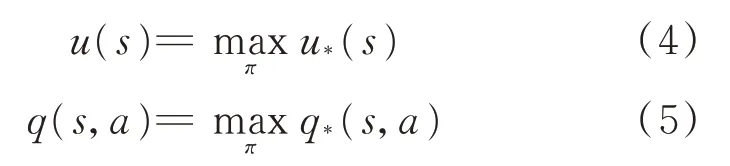
式中：u(s)為所有狀態下最優選擇策略下狀態價值目標函數；q(s，a)為所有狀態下最優選擇策略下動作價值目標函數。

本文目標是輸出從起點到終點的智能決策路徑，路徑決策的依據是Agent在經過學習的過程后，在每一個狀態選擇最大價值動作進行執行。Bellman最優方程計算了各狀態下動作最大價值和狀態最大價值，最優價值函數計算從起始狀態到終止狀態的最大價值動作和狀態的決策序列。

2 時序差分離線控制算法

時序差分離線控制算法Q-Learning［11］是一種基于機器學習的強化學習算法，Q-Learning算法的核心思想是學習一種最優選擇策略，即指導Agent在什么情況下要采取什么行動，該算法可以處理隨機轉換和獎勵的問題，隨機轉換狀態采用ε-greedy策略［12］，該策略會設定一個ε∈(0，1)值，表示Agent有ε概率會選擇當前最大價值動作，有1-ε概率會隨機選擇除最大價值外的動作。

對任何有限MDP問題，Q-Learning總能找到一種最優的策略，即從當前狀態開始，在當前和所有后續狀態轉換中尋求最大總回報的一種策略。在給定無限探索時間和部分隨機策略的情況下，Q-Learning算法可以為任何給定MDP問題確定最佳動作選擇策略。

在本文中，Q-Learning算法的目標是輸出一組Agent到達終點獲得最終獎勵的最優決策序列，此決策序列中每一次狀態轉換均選擇當前狀態最大價值動作。為評估算法收斂性，算法迭代過程中計算每次迭代從起始狀態到終止狀態所運動的次數，用計步器N表示。

對于迭代過程中狀態轉換時動作價值更新，Q-Learning算法引入Q表更新公式［13］：

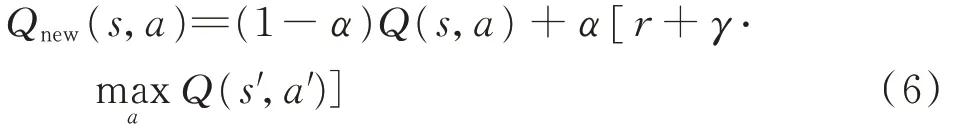
式中：α為學習效率。

Q-Learning算法流程包括四個步驟，算法流程如圖3所示。

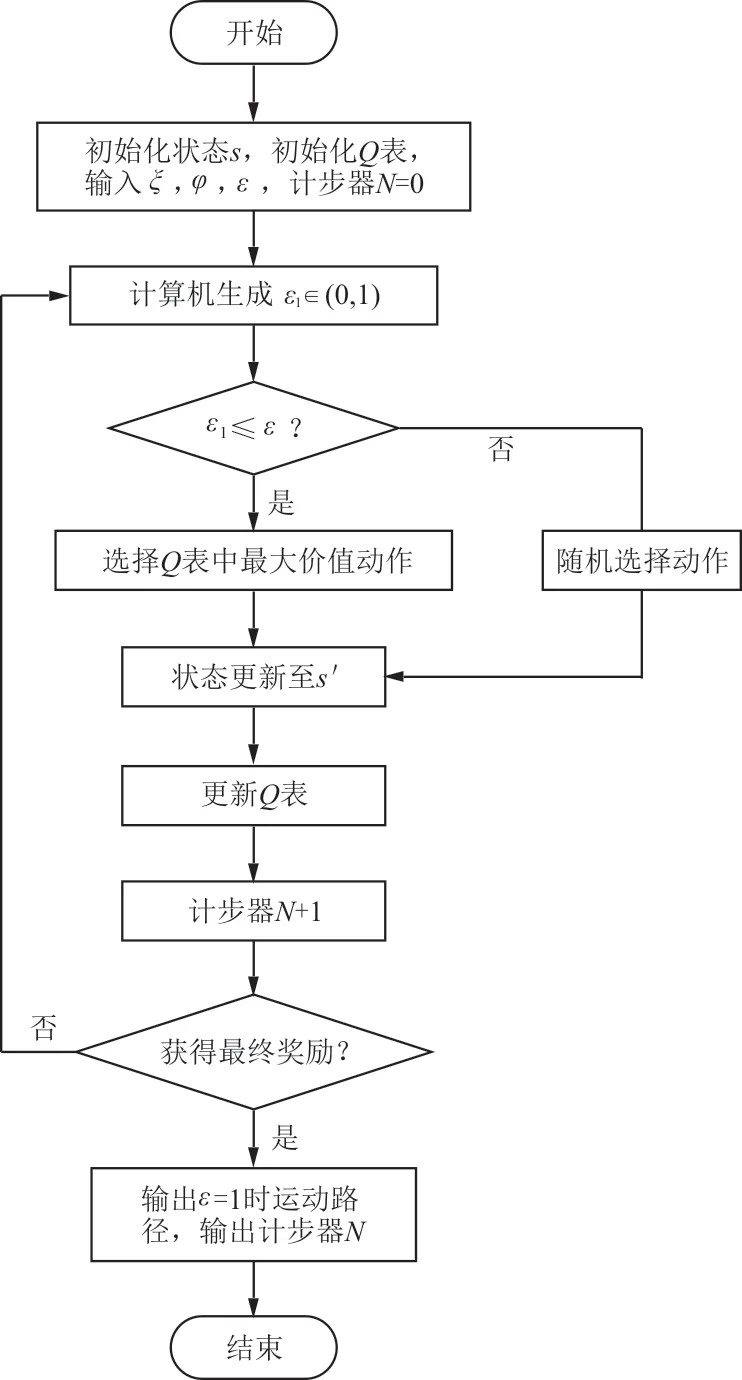
圖3 Q-Learning算法流程Fig.3 The algorithm flow chart of Q-Learning

步驟一：初始化Q表，初始化狀態，設定參數集，導入模擬環境模型。

步驟二：智能體Agent從當前狀態s出發，計算機隨機生成ε1∈(0，1)。

（1）若ε1≤ε，遍歷Q表，選擇Q表中最大價值動作，若有多個最大價值動作，則在此多個動作中隨機選擇動作；

（2）若ε1＞ε，則隨機選擇動作。

步驟三：狀態更新至s′，根據公式（6）更新動作價值，計步器N+1。

步驟四：智能體Agent與模擬環境進行交互。

（1）獲得最終環境獎勵，算法結束；

（2）未獲得最終環境獎勵，返回步驟二。

3 仿真分析

調用Python中的標準TKGUI接口Tkinter模塊編寫海口美蘭機場環境，用填充三角形方格代表停機位區域，黑色方格代表障礙以及非跑道滑行道部分的機場區域。

為考慮所建模型的實際意義，選擇以下兩組模型參數。

模型參數集一：在Agent運動過程中，主要考慮兩個管制員地面管制規則：（1）全跑道起飛；（2）靠近跑道的平行滑行道上航空器滑行方向一致。

獎勵函數中，取跑道出口方格ξ=50，環境障礙方格φ=10。

Q表更新函數中，初始Q表中Q(s，a)=0，α=0.1，γ=0.9［14-15］，ε-greedy策略中ε=0.8。

仿真過程中迭代次數為200次。

模型參數集二：獎勵函數中，取跑道出口方格ξ=50，環境障礙方格φ=10。

Q表更新函數中，初始Q表中Q(s，a)=0，α=0.1，γ=0.9，ε-greedy策略中ε=0.8。

仿真過程中迭代次數為200次。

3.1 數據結果及分析

算法經過200次迭代后ε=1輸出的結果如圖4所示，ε=1表示在所有狀態下選擇所有動作中最大價值動作轉換狀態。圖4中實線表示考慮機場航空器地面滑行規則的滑行路徑，參數按照模型參數集一設置；虛線表示未考慮機場航空器地面滑行規則的滑行路徑，參數按照模型參數集二設置。

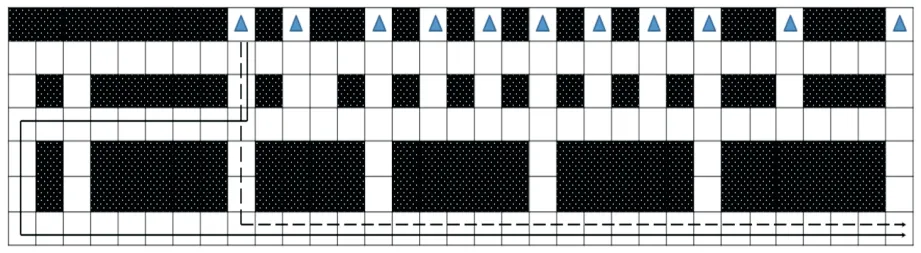
圖4 不同滑行規則下滑行路徑Fig.4 The taxiing path of different taxiing rules

從圖4可以看出：實線路徑中Agent從初始狀態出發，經46次移動到達跑道出口，虛線路徑中Agent從同一初始狀態出發，經30次移動到達跑道出口。兩者相比，實線路徑Agent移動次數雖然增加，但從機場實際運行規范來看，虛線路徑并不符合機場實際運行要求，實線路徑比較符合實際滑行路徑。因此，考慮滑行規則的機場地面航空器強化學習移動模型更接近實際，仿真結果有較高的實際價值。

兩組模型參數的算法迭代曲線如圖5所示，橫軸表示迭代次數，縱軸表示每一次迭代算法輸出計步器N的值，可以看出：在考慮了航空器地面滑行規則后，相當于為航空器智能體添加約束，參數集二的曲線經過56次迭代后趨于收斂，參數集一的曲線經過25次迭代后趨于收斂，算法的收斂速度加快。參數集一曲線收斂后，N值趨近于理論計算值66，說明結果真實有效。

圖5 不同滑行規則下算法迭代曲線Fig.5 The algorithm iteration curve of different taxiing rules

3.2 ε-greedy策略貪婪性分析

由ε-greedy策略定義可知，ε值的大小影響Agent對環境的探索情況。設置ε={0.4，0.6，0.8}三個值探究ε對于算法影響，其余參數按照模型參數集一設置，算法曲線收斂后計步器N結果如表1所示，其中理論值的計算規則為2（1-ε）N。

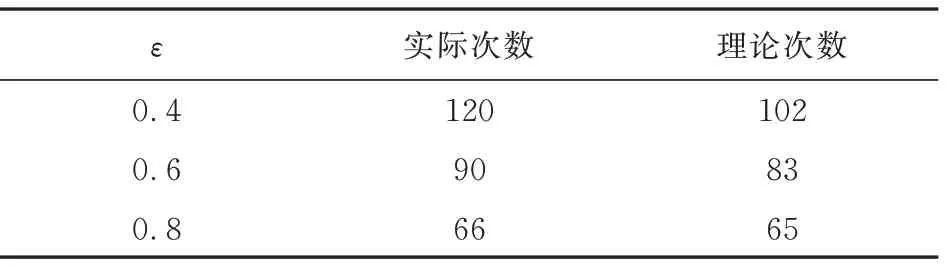
表1 計步器N理論值實際值Table 1 Theoretical value and actual value of step counter N

ε貪婪性對比圖如圖6所示，其中紅線代表ε=0.8時的迭代結果，算法收斂后曲線趨近于定值66；綠線代表ε=0.6的結果，算法收斂后曲線趨近于定值90；粉線代表ε=0.4的實驗結果，算法收斂后曲線趨近于定值120。

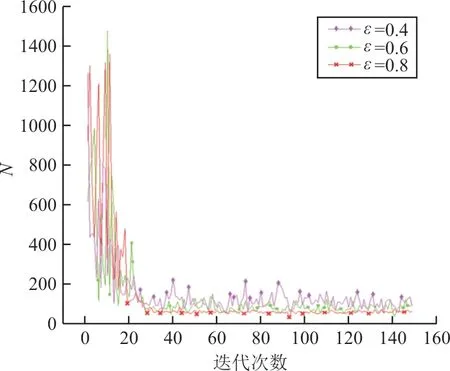
圖6 不同ε值貪婪性對比Fig.6 Comparison greedy of differentεvalues

從圖6可以看出：ε對算法迭代速度影響不大，主要影響了算法曲線收斂后計步器N值的波動情況。

3.3 模型對比分析

相較于傳統的整數線性規劃模型、有向圖及Petri網模型，本文所構建的機場地面航空器移動強化學習模型具備以下優點：

（1）模型無需人工指派停機位、滑行道和跑道等地面滑行資源，通過環境狀態轉換設定獎勵函數的方式由智能體自主識別航空器可滑行區域，智能化程度較高。

（2）模型基于強化學習算法構建，航空器Agent可根據不同的模擬環境學習生成適用于不同機場的靜態路徑，普適性較強。

4 結 論

（1）本文所構建的航空器機場地面移動強化學習模型，通過航空器Agent與機場模擬環境之間的交互，實現了從停機位到跑道出口智能靜態路徑規劃。

（2）模型規劃的路徑與機場航空器實際滑行路徑相符，能輔助塔臺管制員進行初始靜態路徑規劃，具有較高的應用價值。

本文主要考慮航空器Agent與機場模擬環境之間的交互，并未考慮時間序列下多航空器Agent運行之間的沖突交互，這是下一步的研究內容。